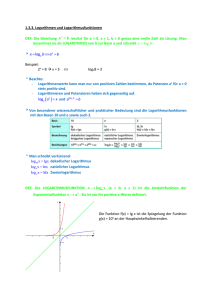
Wöchentliche Aufgabe zur Vorbereitung des Vortrags “Zahlen

Wöchentliche Aufgabe zur Vorbereitung des Vortrags “Zahlen /
Algebra”
Auf der Seite http://www.math.utah.edu/~alfeld/math/sexample.html werden zwei
Herangehensweisen an das Umrechnen von Basen bei Logarithmen dargestellt.
Stellen Sie eine Liste der für den zweiten Ansatz benötigten Definitionen und
Rechengesetze auf.
Überlegen Sie sich (und tragen Sie es in die Liste ein) in welcher Reihenfolge diese
Definitionen und Rechengesetze sinnvollerweise unterrichtet werden können.
Feedback zur 3. wöchentlichen Aufgabe (Zahlen und Algebra)
Wir haben Eure Antworten so angeordnet, dass zuerst die zwei Top-Antworten
kommen, die ihr Euch anschauen solltet; sie sind beide sehr ausführlich. Im letzten
Beitrag ist sehr schön aufgeführt, wie man im zweiten Ansatz von Schritt 1 zu Schritt
2 und Schritt 3 kommt.
Beitrag 1
Notwendig sind beim 2. Ansatz folgende Rechengesetze und Definitionen:
1. Voraussetzung um mit Logarithmen umgehen zu können ist, dass sie in
Beziehung zu den Potenzen stehen.
Dazu benötigt man die Definition des Logarithmus:
log a (b) ( a > 0 ; a ≠ 1 ; b > 0) ist diejenige reelle Zahl c, für die a ^ c = b gilt.
log a (b) = c gdw a ^ c = b
Im Unterricht sollte auf jeden Fall zuerst mit der Definition begonnen werden.
Die Sch. müssen den Zusammenhang zwischen den Potenzen und der neuen
Schreibweise der Logarithmen verstehen und anwenden können. Hierbei wird
erst mit Logarithmen zur Basis 10 angefangen.
2. Man muss wissen, was es für Logarithmen gibt und deren einfachere
Schreibweise kennen.
log e (x) = ln x
log 10 (x) = lg x
natürliche Logarithmen mit der Basis e
dekadische Logarithmen mit der Basis 10
Der nächste Schritt sollte darin bestehen, den Sch. klarzumachen, dass es
Logarithmen mit verschiedener Basis gibt. Nach log 10 (x) sollte auch erwähnt
werden, dass es Logarithmen zur Basis e gibt. Dies ist später bei der
Zeichnung wichtig, da ln x die Umkehrfunktion zu lg x ist.
Die kürzere Schreibweise ist einzuführen.
3. Man muss wissen, dass man durch beidseitiges logarithmieren, die
Hochzahlen „runterholen“ kann.
Dabei muss die Basis gleich sein. Hier wird mit einem natürlichen Logarithmus
multipliziert.
Æ ln 2 ^ log 2 (x) = ln x
Æ log 2 (x) * ln 2 = ln x
Wenn die Sch. das umrechnen beherrschen, sollte man wichtige
Rechengesetze bei Log. einführen. Auch, wie man in eine unterschiedliche
Basis umrechnet.
4. Durch normale Termumformung erhält man log 2 (x) = ln x / ln 2
indem man durch ln 2 teilt.
Dies beinhaltet ein weiteres Umformungsgesetz mit Basis e: log a (b) = ln b / ln a
Die Termumformung muss denn Sch. bereits bekannt sein.
Kommentar:
Hier haben wir nichts hinzuzufügen.
Beitrag 2
Zunächst muss der Logarithmusbegriff eingeführt werden:
Nämlich wenn gilt bx = y, so ist logby = x, mit b...Basis, x...Exponent, y...Potenz
Aus dieser Definition folgt logischerweise:
Es gilt blogby = y, da nach der Definition des Logarithmus logby = x und bx = y
Anschließend bietet es sich an, die drei Logarithmusgesetze durchzunehmen; Das
erste wird für das Verständnis des Dritten benötigt, das zweite könnte man in diesem
Zusammenhang auch weglassen, der Vollständigkeit halber würde ich es aber in
diesem Zusammenhang mit einführen, da es später auf jeden Fall noch benötigt wird.
1. logb(u*v) = logbu + logbv
2. logb(u/v) = logbu - logbv
3. logbun = n*logbu, da x = un Æ logbun = logb(u * u * u * …* u)
= logbu + logbu + logbu + ... + logbu
= n*logbu
Nun müssen die Schüler noch wissen, dass Logarithmen zum Gleichungslösen
benutzt werden können; eine Gleichung ändert sich also nicht, wenn man auf beiden
Seiten logarithmiert. Hierzu wird der Zehnerlogarithmus oder der natürliche
Logarithmus benutzt.
Zum Beispiel: x = a * b / ln
Ln x = ln (a*b)
Ln x = lna + lnb
Ist dies alles bekannt, so müssten die Schüler den zweiten Ansatz verstehen.
Kommentar:
Auch hier haben wir nichts hinzuzufügen.
Beitrag 3
2. Ansatz:
•
•
•
•
2log2(x) = x
log2 (x) * ln (2) = ln (x)
aus (2) folgt:
log2 (x) = ln (x) / ln (2)
(1)
(2)
Definitionen/ Einführung im Unterricht
1. Einführen einer neuen Rechenart: Definition des Logarithmus, damit Schüler
sich unter dem nicht allzu gebräuchlichen Namen etwas vorstellen können.
2. Für was braucht man den Logarithmus? Um Gleichung nach einer Hochzahl
aufzulösen.
3. Verschiedene Logarithmen:
Natürlicher Log.: ln x
Dekadischer Log. Lg x
Basis e (Eulersche Zahl)
Basis 10 (log 10 x)
4. Eigenschaften der Logarithmen; von Funktionsgraphen, theoretischen
Bezeichnungen oder von Exponentialfunktion (Umkehrfunktion des Log.)
Berechnung mit leicht zu berechnenden Zahlen; konkrete Lösung.
5. Rechenregeln/ Gesetze:
1. Logarithmengesetz: log a (u*v) = loga u + loga v
loga (u / v ) = loga u – loga v
2. Logarithmengesetz: loga xn = n* loga x
6. Anwendung der Gesetze
Kommentar:
Guter Ansatz zum Unterrichten an der Schule, doch leider können wir keine
konkrete Liste von Definitionen und Rechengesetzen erkennen, die für den
zweiten Ansatz nötig sind.
Beitrag 4
Benötigte Definitionen und Rechengesetze
Liste:
1. Begriffserklärung:
Logarithmus logar
Jede positive Zahl r >0 ist als Potenz einer beliebigen Basis a >0, a ≠ 1 in der Form r
= ax darstellbar. Die eindeutig bestimmte Lösung x der Gleichung r = ax heißt
Logarithmus von r zur Basis a. Die symbolische Schreibweise hierzu lautet:
x = logar wobei r: Numerus (r >0) und a: Basis (a >0, a ≠ 1)
2. Anmerkungen
™ Logarithmen können nur von positiven Zahlen gebildet werden und sind noch von
der
Basis abhängig.
™ Für jede zulässige Basis a gilt: logaa = 1
loga1 = 0
x
™ loga (a ) = x für a >0, a ≠ 1 und x Element R
™ a logax = x
für a >0 a ≠ 1 und x >0
3. Rechenregeln für Logarithmen
(1) loga (u*v) = loga u + loga v
(2) loga (u/v) = loga u - loga v
(3) loga (uv) = k* logau
(4) loga n√u = (1/n) * logau
4. Umgang mit Logarithmus
Den Schülern muss klargemacht werden, dass sich eine Gleichung nicht ändert,
wenn man auf beiden Seiten logarithmiert. Sie lernen, die Rechenregeln
anzuwenden.
Kommentar:
Es sind zwar alle Definitionen und Rechengesetze vorhanden, doch erkennen
wir nicht, wie wir sie in der Liste für den zweiten Ansatz einordnen sollen.
Beitrag 5
Liste der für den zweiten Ansatz benötigten Definitionen und Rechenregeln:
(Schreibweise entspricht der Maple-Notation)
Definitionen:
1) log[a](u)=x
2) a^log[a](x)=x
Rechengesetz:
{1,2,3,…}
(für: a, u > 0; a ungleich 1)
(für: a > 0; a ungleich 1)
3) log[a](u^k)=k*log[a](u) (für: a, u > 0; a ungleich 1; k =
Aus der allgemeinen Logarithmus-Definition, die am Anfang der Unterrichtseinheit
stehen wird, leitet sich die zweite Definition sofort ab. Anschließend wird man zu den
Rechengesetzen übergehen.
Kommentar:
Der erste Schritt des zweiten Ansatzes ist erklärt, doch welche Definitionen
und Rechengesetze für den zweiten und dritten Schritt nötig sind, fehlen. Die
Reihenfolge, wie Du es in der Schule unterrichten würdest ist klar, doch wenig
umfangreich beschrieben.
Beitrag 6
Notwendige Definitionen:
a^x = b ⇒ x = log a (b)
log a (b) = lg b/lg a
Die erste Definition muss vor der zweiten kommen, weil sie zeigt, wofür man den
Logarithmus eigentlich braucht, nämlich für die Berechnung von x, wenn das x im
Exponenten vorkommt.
Der Logarithmus kann auch im Exponenten stehen, wie man darauf bei dem Beispiel
kommt, ist mir jedoch leider nicht klar! (Auf dem Gymnasium ging es immer nur um
das Ableiten von e und ln, weil man nur dies für die Abiturprüfung benötigte!)
Warum ich a=2 und b=e setzen muss, ist mir auch nicht klar, aber Logarithmen zur
Basis e sind natürliche Logarithmen und welche zur Basis 10 sind gewöhnliche oder
Zehner- logarithmen.
Kommentar:
Schau Dir einfach die ersten beiden Lösungen an, dann wird es Dir klar. Sie
sind sehr gut erklärt.
Beitrag 7
2. Ansatz:
log2 (x) = ln(x)/ln(2)
log2 (x) * ln(2) = ln(x)
Liste für Definitionen und Rechengesetze:
1.
log10 (x) = a
10a = x
2.
loga 1 = 0
loga a = 1
3.
loga an = n
4.
loga (b) = logc (b)/logc (a)
Kommentar:
Kaum zu erkennen, wie die Definitionen und Rechengesetze in die Liste des
zweiten Ansatzes einzureihen sind. Auch wird nicht klar, wie Du es
unterrichten würdest. Schau Dir einfach die ersten beiden Lösungen an; sie
sind sehr gut erklärt.
Beitrag 8
bx = c ( b ∈ 3+ ∧ c ∈ 3+)
Berechnung des Exponenten:
- x = logb c ( b ∈ 3+ /n1o )
- ln ab = b · ln a
2log2(x) = x | ln
I
II
Nr.: aus II folgt: ln 2log2(x) = log2(x) · ln 2
log2(x) · ln 2 = ln x | : ln 2
log2(x) = ln (x)/ln 2
Kommentar:
Sehr gut erkennbar, wie man im zweiten Ansatz von Schritt 1 zu Schritt 2 und
Schritt 3 kommt. Doch leider eine unvollständige Liste von Definitionen und
Rechengesetzen. Auch nicht erkennbar, wie Du es unterrichten würdest.