1. Haftung - Ing. Johannes Wandinger

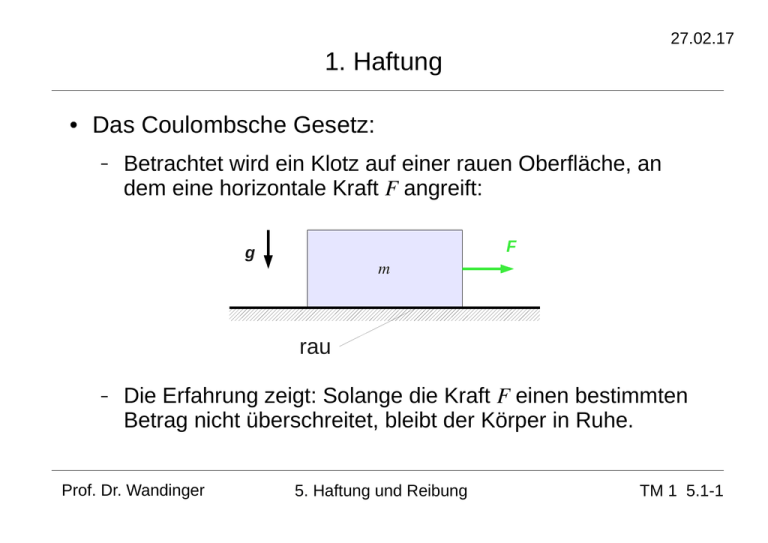
27.02.17
1. Haftung
●
Das Coulombsche Gesetz:
–
Betrachtet wird ein Klotz auf einer rauen Oberfläche, an
dem eine horizontale Kraft F angreift:
F
g
m
rau
–
Die Erfahrung zeigt: Solange die Kraft F einen bestimmten
Betrag nicht überschreitet, bleibt der Körper in Ruhe.
Prof. Dr. Wandinger
5. Haftung und Reibung
TM 1 5.1-1
27.02.17
1. Haftung
–
Gleichgewicht:
∑ F x =0
∑ F y=0
: −H + F =0 → H =F

G
F
: −G + N =0 → N =G
–
Der Körper haftet für F =H < H 0 .
–
Coulombsches Gesetz:
–
Haftbedingung:
H 0 =μ 0 N
y
H
N
x
H < H 0 =μ 0 N
Prof. Dr. Wandinger
5. Haftung und Reibung
TM 1 5.1-2
27.02.17
1. Haftung
–
Die Haftungskraft ist so gerichtet, dass die Bewegung verhindert wird.
–
Der maximale Wert H0 ist näherungsweise proportional zur
Normalkraft N.
–
Der Proportionalitätsfaktor μ0 heißt Haftungskoeffizient oder
Haftzahl.
–
Der Haftungskoeffizient hängt vom Material und der Beschaffenheit der Oberflächen ab.
–
Der Angriffspunkt der Normalkraft N kann aus dem Momentengleichgewicht bestimmt werden.
Prof. Dr. Wandinger
5. Haftung und Reibung
TM 1 5.1-3
27.02.17
1. Haftung
●
Typische Werte des Haftungskoeffizienten μ0:
Stahl auf Eis
0,03
Stahl auf Stahl (blank)
0,1 … 0,15
Stahl auf Stahl (rostig)
0,3 … 0,8
Stahl auf Teflon
0,04
Leder auf Grauguss
0,2 … 0,3
Leder auf Metall
0,2 … 0,6
Holz auf Holz
0,5
Autoreifen auf Straße
0,7 … 0,9
Ski auf Schnee
0,1 … 0,3
Prof. Dr. Wandinger
5. Haftung und Reibung
TM 1 5.1-4
27.02.17
1. Haftung
●
Haftungswinkel:
–
Der Haftungswinkel gibt die
maximal mögliche Abweichung der Wirkungslinie der
Reaktionskraft von der Normalenrichtung an, bei der
noch Gleichgewicht herrscht.
G
Fmax
N
ρ0
tan (ρ 0 )=
Prof. Dr. Wandinger
5. Haftung und Reibung
H0
A
H0
N
=μ 0
TM 1 5.1-5
27.02.17
1. Haftung
–
Gleichgewicht ist möglich, wenn die benötigte Reaktionskraft innerhalb des Haftungskeils bzw. Haftungskegels liegt.
Haftungskeil:
Haftungskegel:
ρ0
A
A
Prof. Dr. Wandinger
5. Haftung und Reibung
ρ0
TM 1 5.1-6
27.02.17
1. Haftung
●
Beispiel 1: Schiefe Ebene
–
Gegeben:
●
–
Haftungskoeffizient
μ0 = 0,2
Gesucht:
●
mg
Winkel α0 , bei dem der
Körper anfängt zu gleiten
α
Prof. Dr. Wandinger
5. Haftung und Reibung
TM 1 5.1-7
27.02.17
1. Haftung
–
Gleichgewicht:
∑ F x =0
: H −m g sin (α)=0

H
→ H =m g sin (α)
∑ F y=0
: N −m g cos (α)=0
→ N =m g cos (α)
–
α
y
x
N
mg
Haftbedingung:
H < H 0 =μ 0 N → m g sin (α)<μ 0 m g cos (α) → tan (α)<μ 0
→ α<α 0 =ρ0 (Haftungswinkel)
–
Zahlenwert:
Prof. Dr. Wandinger
tan (α 0 )=0,2 → α 0 =11,3°
5. Haftung und Reibung
TM 1 5.1-8
27.02.17
1. Haftung
●
Beispiel 2: Keilnut
–
A
–
Gegeben:
●
Anpresskraft A
●
Keilwinkel α
●
Haftungskoeffizient μ0
Gesucht:
●
F
durch Haftung übertragbare Kraft F
α
Prof. Dr. Wandinger
5. Haftung und Reibung
TM 1 5.1-9
27.02.17
1. Haftung
Kräfte am Keil:
–
α/2
z
A
x
y
A
α/2

H
N
α
z
F
Prof. Dr. Wandinger
N
5. Haftung und Reibung
N
y
TM 1 5.1-10
27.02.17
1. Haftung
–
Gleichgewicht am Keil:
∑ F x =0
N
A
–
: F −2 H =0
→ F =2 H
H 0 =μ 0 N
μ0 A
→ F =2 H 0 =
sin (α /2)
=μ ' 0 A
α/2
α/2
1
A=N sin α
2
2
N
–
( )
A
→ N=
2 sin ( α/2 )
Prof. Dr. Wandinger
Maximale Haftungskraft
pro Fläche:
Der Koeffizient
μ0
μ ' 0=
>μ 0
sin ( α/2 )
heißt Keilnuthaftzahl.
5. Haftung und Reibung
TM 1 5.1-11
27.02.17
1. Haftung
●
Beispiel 3: Leiter
–
Auf der dargestellten Leiter
steht ein Mann der Masse m.
–
Wie hoch kann er steigen,
wenn die Wand als glatt betrachtet wird?
–
Gegeben:
mg
h
y
ϕ
–
●
Haftungskoeffizient μ0
●
Höhe h, Winkel ϕ
Gesucht:
●
Prof. Dr. Wandinger
maximale Höhe y
5. Haftung und Reibung
TM 1 5.1-12
27.02.17
1. Haftung
A
M
∑ =0 : −h N B + x mg=0
x
→ N B= m g
h
Gleichgewicht:
–
NB

B
mg
h
y
–
ϕ
A
HA
∑ F x =0
:−H A+ N B =0 → H A=N B
∑ F y=0
: N A−mg=0 → N A=m g
Haftbedingung:
N B =H A <μ 0 N A
x
y
NA
x
Prof. Dr. Wandinger
x
→
m g <μ 0 m g
h
→ x <μ 0 h
y= x tan (ϕ)<μ 0 h tan (ϕ)
5. Haftung und Reibung
TM 1 5.1-13
27.02.17
1. Haftung
–
Wird auch im Punkt B eine Haftungskraft zugelassen, so
treten vier unbekannte Reaktionskräfte auf. Die Leiter ist
dann statisch unbestimmt gelagert.
–
Mithilfe der Haftungskeile in den Lagerpunkten A und B
lässt sich graphisch ermitteln, unter welchen Bedingungen
Gleichgewicht möglich ist.
–
Die Leiter ist im Gleichgewicht, wenn sich die Wirkungslinien der Reaktionskräfte in den Punkten A und B und der
Gewichtskraft in einem Punkt schneiden.
Prof. Dr. Wandinger
5. Haftung und Reibung
TM 1 5.1-14
27.02.17
1. Haftung
–
Gleichgewicht ist möglich,
wenn sich die Wirkungslinien im schraffierten Gebiet schneiden.
Grenzlage
B
B
mg
A
A
Prof. Dr. Wandinger
5. Haftung und Reibung
TM 1 5.1-15
27.02.17
1. Haftung
●
Beispiel 4: Klemmhalterung
b
a
A
–
Der Stab mit Gewicht GS wird
von zwei Klemmbacken mit
Gewicht GB gehalten.
–
Gegeben:
α
GB
GB
y
GS
x
Prof. Dr. Wandinger
B
–
●
Gewicht GB
●
Abmessungen a, b
●
Haftungskoeffizient μ0
●
Winkel α
Gesucht:
●
maximales Stabgewicht GS
5. Haftung und Reibung
TM 1 5.1-16
27.02.17
1. Haftung
–
Gleichgewicht am Stab:
∑ F x =0

d
N1
y
→ N 1 =N 2= N
P
H1
N2
H2
GS
d
d
∑ M =0 : 2 H 2− 2 H 1=0
→ H 1 =H 2=H
P
∑ F y=0
x
Prof. Dr. Wandinger
: N 1− N 2 =0
: H 1 + H 2−G S =0
→ G S =2 H
5. Haftung und Reibung
TM 1 5.1-17
27.02.17
1. Haftung
–
Gleichgewicht am Klemmbacken:

A
M
∑ =0 :
−a G B −b H +b tan (α) N =0
N
α
Ax
A
Ay
GB
a
b
a
→ N = H + G B cot (α)
b
(
H
)
y
x
Prof. Dr. Wandinger
5. Haftung und Reibung
TM 1 5.1-18
1. Haftung
–
27.02.17
Haftbedingung:
a
H <μ 0 N =μ 0 H + G B cot (α)
b
a
a
→ ( 1−μ 0 cot (α) ) H <μ 0 G B cot (α) → ( tan (α)−μ 0 ) H <μ 0 G B
b
b
(
–
)
Es müssen drei Fälle unterschieden werden:
●
Für tan(α)>μ 0 gilt:
2 μ0
a
a
H<
G B → G S =2 H <
GB
tan(α)−μ 0 b
tan (α)−μ 0 b
μ0
Prof. Dr. Wandinger
5. Haftung und Reibung
TM 1 5.1-19
1. Haftung
●
Für tan (α)=μ 0 gilt:
a
0<μ 0 G B
b
●
Für tan (α)<μ 0 gilt:
tan (α)−μ 0 <0
27.02.17
μ0
a
a
−( μ 0 −tan(α) ) H <μ 0 G B → −H <
GB
b
μ 0 −tan(α) b
●
Die Bedingungen für tan (α)≤μ 0 sind immer erfüllt. Das
Stabgewicht GS kann beliebig groß werden. Dieser Fall wird
als Selbsthemmung bezeichnet.
Prof. Dr. Wandinger
5. Haftung und Reibung
TM 1 5.1-20