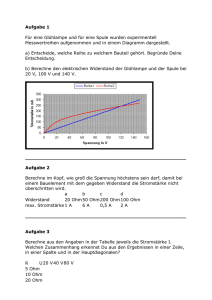
Elektrischer Strom - Gleichstromkreise

Musso: Physik II
Teil 25 Gleichstromkreise
Seite 1
ELEKTRIZITÄT UND MAGNETISMUS
Tipler-Mosca
25. Elektrischer Strom - Gleichstromkreise (Electric current and directcurrent circuits)
25.1 Elektrischer Strom und die Bewegung von Ladungsträgern (Current and the motion of
charges)
25.2 Widerstand und Ohm'sches Gesetz (Resistance and Ohm's law)
25.3 Energetische Betrachtungen elektrischer Stromkreise (Energy in electric circuits)
25.4 Zusammenschaltungen von Widerständen (Combinations of resistors)
25.5 Die Kirchhoff'schen Regeln (Kirchhoff's rules)
25.6 RC-Stromkreise (RC circuits)
Universität Salzburg
Seite 1
09.04.2007
Musso: Physik II
Universität Salzburg
Teil 25 Gleichstromkreise
Seite 2
Seite 2
09.04.2007
Musso: Physik II
Teil 25 Gleichstromkreise
25.1 Elektrischer Strom und die Bewegung von Ladungsträgern (Current and the motion of charges)
Seite 3
Die Rate, mit der elektrische Ladungen durch eine Fläche A fließt, bezeichnet man als elektrischer Strom
Gleichstromkreise: Stromkreise, in denen sich die Richtung des Stromes nicht ändert;
Wechselstromkreise: Stromkreise, in denen sich die Richtung des Stromes ständig ändert (siehe Teil 29)
SI-Einheit des Stromes I : Ampere (A) ⇔ 1 A = 1 C s-1; siehe auch Teil 26, Definition des Ampere anhand
der Kraft, die zwei stromdurchflossene Leiter aufeinander ausüben.
Vereinbarung: Richtung des Stromes = Bewegungsrichtung der positiv geladenen Ladungsträger ⇒ Elektronen
bewegen sich entgegengesetzt der konventionellen Stromrichtung.
Bewegung freier Elektronen durch einen leitfähigen Draht ⇒
Kein elektrisches Feld am Draht anliegend ⇒ Elektronen bewegen sich in zufälligen Richtungen ⇒ stoßen
mit den Gitterionen zusammen ⇒ mittlere Geschwindigkeit der Elektronen = null.
Elektrisches Feld am Draht anliegend ⇒ Kraft − eE auf jedes freie Elektron ⇒ Beschleunigung entgegengesetzt
zur Feldrichtung ⇒ stoßen mit den Gitterionen zusammen ⇒ durch ständiges Wechsel von Beschleunigung
und Energieumwandlung ⇒ Elektronen driften entgegengesetzt zur Feldrichtung mit der Driftgeschwindigkeit v d .
Sei n = N / V die Anzahldichte der Ladungsträger (= Anzahl freier
Ladungsträger pro Volumseinheit) in einem Leiter mit der
Querschnittsfläche A. Die Ladungsträger mit jeweils Ladung q bewegen
sich mit v d senkrecht zu A. Während Δt gelangen alle Ladungsträger
aus dem Volumen ΔV = Av d Δt durch die Fläche A ⇒ innerhalb ΔV ist
die Teilchenzahl ΔN = nAv d Δt ⇒ die Ladung Δq = qnAv d Δt
Universität Salzburg
Seite 3
⇒
09.04.2007
Musso: Physik II
Teil 25 Gleichstromkreise
Strom durch die Bewegung beliebiger Ladungsträger I =
Seite 4
Δq
= qnAv d
Δt
Die Anzahldichte n der Ladungsträger in einem Leiter
kann man mit dem Hall-Effekt messen (siehe Teil 26)
⇒ Metalle: ca. 1 freies Elektron pro Atom
Beispiel 25.1: Berechnung der Driftgeschwindigkeit
Kupferdraht mit Durchmesser d = 1.63 mm ⇒ Annahme für Kupfer: ein freies Elektron pro Atom,
gesucht: Driftgeschwindigkeit v d der Elektronen bei I = 1 A ⇒
I
;
qnA
aus Annahme für Kupfer: ein freies Elektron pro Atom ⇒ Anzahldichte der Ladungsträger = Anzahldichte der Atome
es gilt Gl. (25.3) I = qnAv d ⇒ v d =
⇒ aus Molmasse MCu = 63.5 g mol-1, Avogadro-Zahl N A = 6.02 × 10 23 Atome mol-1, und ρCu = 8.93 g cm-3 ⇒
m
N
=
MCu NA
⇒ n = nCu =
NCu
N m
N
6.02 × 1023 Atome mol-1
= A
= A ρ=
8.93 g cm-3 = 8.47 × 1022 Atome cm-3 =
-1
V
MCu V
MCu
63.5 g mol
= 8.47 × 1028 Atome m-3 ;
(1.63 mm)
d2
=π
= 2.087 × 10−6 m2
Querschnittsfläche A des Drahtes: A = π
4
4
−19
C ⇒
Ladung q der Ladungsträger: q = −e = 1.60 × 10
2
I
1 C s-1
vd =
=
qnA
−1.60 × 10 −19 C 8.47 × 1028 m-3
(
)(
)( 2.087 × 10
−6
m
2
)
= −3.54 × 10 −5 m s-1 = −3.54 × 10 −2 mm s-1
Beispiel 25.2: Berechnung der Anzahldichte der Ladungsträger
mögliches Prüfungsbeispiel
Universität Salzburg
Seite 4
09.04.2007
Musso: Physik II
Teil 25 Gleichstromkreise
25.2 Widerstand und Ohm'sches Gesetz (Resistance and Ohm's law)
Seite 5
Ein elektrischer Strom fließt, wenn innerhalb eines Leiters ein elektrisches Feld E herrscht, welches auf die freien
Ladungsträger die Kraft qE ausübt ⇔ E zeigt in Stromrichtung bzw. in Richtung des abnehmedem Potentials
(d.h von φa nach φb ) ⇒ Voraussetzung: homogenes elektrisches Feld E
⇒ Spannung zwischen Punkt a und Punkt b: U = φa − φb = E ΔL
⇒
U
I
wobei SI-Einheit des Widerstands R: Ohm (Ω) ⇔ 1 Ω = 1 V A -1
Quotient aus Spannung und Strom ⇔ Widerstand R =
Der Widerstand R vieler Materialien, insbesondere der
Ohm'sches Gesetz
nicht befolgt
meisten Metalle, hängt weder der Spannung noch vom
Strom ab ⇔ Ohm'sches Verhalten
Aus experimentellen Beobachtungen: Widerstand eines Leiters
proportional zu dessen Länge und umgekehrt proportional
zu dessen Querschnitt A ⇒ R = ρ
A
wobei ρ spezifischer Widerstand, SI-Einheit Ω m
1
ρ
elektrische Leitfähigkeit, SI-Einheit Siemens (S),
1 S = 1 Ω -1 m-1
Universität Salzburg
Ohm'sches Gesetz befolgt
Seite 5
09.04.2007
Musso: Physik II
Teil 25 Gleichstromkreise
Seite 6
Der spezifische Widerstand aller Metalle ist temperaturabhängig
α=
( ρ − ρ20°C ) / ρ20°C
T [°C] − 20°C
Die Querschnitte von Leitungsdrähten sind genormt
Beispiel 25.3: Länge eines Widerstandsdrahts
(
)
Draht aus Nichrom ρ = 10 −6 Ω m mir Radius r = 0.65 mm. Gesucht: Länge
für R = 2 Ω ⇒ aus Gl. (25.8) R = ρ
=
RA
ρ
=
Rπ r 2
ρ
=
( 2 Ω ) π ( 0.65 mm )
Universität Salzburg
10 −6 Ω m
A
⇒
2
= 2.65 m
Seite 6
09.04.2007
Musso: Physik II
Farbcode für Widerstände und andere
Teil 25 Gleichstromkreise
Beispiel 25.4: Widerstand pro Längeneinheit
Bauelemente
Mögliches Prüfungsbeispiel
Seite 7
Beispiel 25.5: Elektrisches Feld in einem Strom führenden Draht
Kupferdraht, Querschnitt 1.5 mm2 , durch den
Draht fließt I = 1.3 A; gesucht: elektrisches Feld E
⇒ elektrisches Feld = Potentialdifferenz pro
Längeneinheit ⇒ E =
U
U
=
aus U = IR ⇒ E =
mit
R
E =I
,
IR
=I
R
⇒
= 1.13 × 10 −2 Ω m-1 ⇒
R
(
)
= (1.3 A ) 1.13 × 10 −2 Ω m-1 = 1.47 × 10 −2 V m-1
Farbig kodierte Kohleschichtwiderstände
Universität Salzburg
Seite 7
09.04.2007
Musso: Physik II
Teil 25 Gleichstromkreise
25.3 Energetische Betrachtungen elektrischer Stromkreise (Energy in electric circuits)
Seite 8
Herrscht in einem Leiter ein elektrisches Feld, so verrichtet es Arbeit an den freien Elektronen, und die Energie des
Elektronengases nimmt zu. Nach kurzer Zeit stellt sich jedoch ein Gleichgewicht, weil die erworbene kinetische
Energie durch Zusammenstöße der Ladungsträger mit Gitterionen ständig in thermische Energie (Joule'sche Wärme)
umgewandelt wird. Durch den Draht fließe ein stationärer Strom ⇒ eine Ladungsmenge ΔQ fließt von links nach
rechts ⇒ Änderung ΔE el der elektrischen Energie von ΔQ : ΔEel = ΔQ (φb − φa ) ⇒ da φa < φb
⇒ ΔE el < 0 ⇒ Energieverlust ⇒ mit U = φa − φb
⇒ − ΔE el = ΔQU
⇒
ΔE el ΔQ
=
U = IU ⇒ Der Verlust an elektrischer Energie pro Zeiteinheit entspricht
Δt
Δt
der im Leiterabschnitt umgesetzte Leistung P = IU
Verlustrate −
gilt für alle Bauelemente beliebiger Stromkreise
An einem Widerstand wird elektrische Energie in Form von Wärme an die Umgebung
abgeführt ⇒ mit Gl. (25.7) U = IR
⇒ P = UI = RI 2 = U 2 / R
Beispiel 25.6: In einem Widerstand umgesetzte Leistung
Durch einen Ohm'schen Widerstand, R = 12 Ω, fließt ein Strom I = 3 A. Gesucht: umgesetzte Leistung ⇒
aus Gl. (25.11) P = RI 2 ⇒ P = (12 Ω )( 3 A ) = 108 W
2
Universität Salzburg
Seite 8
09.04.2007
Musso: Physik II
Spannungsquellen und Quellenspannungen
Teil 25 Gleichstromkreise
Seite 9
Um einen stationären Strom durch einen Leiter aufrechtzuerhalten, muß durch
eine Spannungsquelle ständig elektrische Energie zugeführt werden.
Die Spannungsquelle verrichtet Arbeit an den hindurchtretenden Ladungen,
deren elektrische Energie dadurch zunimmt.
Die pro Ladungseinheit verrichtete Arbeit ist die Quellenspannung UQ
(früher elektromotorische Kraft).
An den Polen einer idealen Spannungsquelle kann unabhängig vom
fließenden Strom stets die gleiche Quellenspannung abgegriffen werden.
Die Ladung innerhalb der Spannungsquelle fließt vom niedrigen zum
höheren Potential, wodurch die elektrische Energie um ΔqUQ zunimmt.
Im Widerstand wird die elektrische Energie in Wärme umgewandelt ⇒
Δq
von der Spannungsquelle abgegebene Leistung P =
UQ = IUQ
Δt
Spannungsquelle
einfacher Stromkreis mit
idealer Spannungsquelle
Ladungspumpe
Zitterrochen: bis 50 A bei 50 V
Universität Salzburg
Seite 9
09.04.2007
Musso: Physik II
Teil 25 Gleichstromkreise
Seite 10
An den Polen einer realen Spannungsquelle greift man
die Klemmenspannung UK ab, die niedriger als UQ ist.
Reale Spannungsquelle: Kombination aus idealer
Rin
Spannungsquelle mit Quellenspannung UQ und aus
UQ
einem Innenwiderstand Rin .
UQ
UK
aus φa = φb + UQ − IRin
⇒ Klemmenpannung UK = φa − φb = UQ − IRin
Spannungsabfall UR am Ohm'schen Widerstand:
UR = RI = φa − φb = UQ − RinI
⇒ I=
UQ
R + Rin
Auf Batterein und Akkumulatoren: Angabe (in A h) der insgesamt entnehmbare Ladung:
1 A h = 1 C s-1 3600 s = 3600 C ⇒ gespeicherte Energie: E el = entnehmbare Ladung × Quellspannung = qUQ
Beispiel 25.7: Klemmenspannung, Leistung, und gespeicherte Energie
Ohm'scher Widerstand R = 11 Ω mit Batterie verbunden (UQ = 6 V, Rin = 1 Ω, 150 A h).
Beispiel 25.8:
Maximal abgegebene Leistung
mögliches Prüfungsbeispiel
Gesucht: a) Strom I , b) Klemmenspannung UK , c) die von der Spannungsquelle
abgegebene Leistung P, d) die am Ohm'schen Widerstand umgesetzte Leistung,
e) die am Innenwiderstand umgesetzte Leistung, f) die Energie der Batterie
⇒
( R + Rin ) = ( 6 V ) (11 Ω + 1 Ω ) = 0.5 A;
Teil b) mit Gl. (25.13) φa − φb = UQ − RinI = 6 V − (1 Ω )( 0.5 A ) = 5.5 V;
Teil c) mit Gl. (25.12) PQ = IUQ = ( 0.5 A )( 6 V ) = 3 W
2
2
Teil d) mit Gl. (25.11) PR = I 2 R = ( 0.5 A ) (11 Ω ) = 2.75 W; Teil e) Pin = I 2 Rin = ( 0.5 A ) (1 Ω ) = 0.25 W
Teil f) mit Gl. (25.15) Eel = qUQ = (150 A h )( 6 V ) = 150 ( 3600 C ) ( 6 V ) = 3.24 MJ
Teil a) mit Gl. (25.14) I = UQ
Universität Salzburg
Seite 10
09.04.2007
Musso: Physik II
Teil 25 Gleichstromkreise
25.4 Zusammenschaltungen von Widerständen (Combinations of resistors)
Seite 11
Vereinfachung der Analyse von Stromkreisen: mehrere Widerstände durch einen einzigen Widerstand ersetzt.
Reihenschaltung von Widerständen
Serienschaltung oder Reihenschaltung: der gleiche Strom fließt durch beide Widerstände ⇒
Gesamtspannungsabfall UR = R1I + R2I = I ( R1 + R2 ) = IR ⇒ R = R1 + R2
Parallelschaltung von Widerständen
Parallelschaltung: die gleiche Spannung fällt über alle Widerstände ab ⇒
an den Knotenpunkten a und b gilt: I = I1 + I2 wobei I1 und I2 Teilströme ⇒
Spannungsabfall UR = I1R1 = I2 R2 ; für den Ersatzwiderstand UR = IR ⇒
aus I = I1 + I2 ⇒
Universität Salzburg
⎛ 1
UR U R UR
1 ⎞
=
+
= UR ⎜
+
⎟
R
R1 R2
⎝ R1 R2 ⎠
⇒
1
1
1
=
+
R R1 R2
Seite 11
09.04.2007
Musso: Physik II
Teil 25 Gleichstromkreise
Seite 12
Beispiel 25.9: Parallel geschaltete Ohm'sche Widerstände
An zwei parallel geschalteten Ohm'sche Widerständen,
R1 = 4 Ω und R2 = 6 Ω, liegt eine Spannung UQ = 12 V an.
Gesucht: a) Ersatzwiderstand R, b) ingesamt fließender Strom I, c) die durch die Widerstände fließende
Teilströme I1 und I2 , d) in in den einzelnen Winderständen umgesetzte Leistung, e) die von der Batterie
abgegebene Leistung
Teil a) mit Gl. (25.21)
⇒
1
1
1
=
+
R R1 R2
⇒ R=
( 4 Ω )( 6 Ω ) = 2.4 Ω
R1R2
=
R1 + R2
4 Ω+6 Ω
Teil b) mit Gl. (25.20) I = UR R = (12 V ) ( 2.4 Ω ) = 5 A,
Teil c) mit Gl. (25.19) I1 = UR R1 = (12 V ) ( 4 Ω ) = 3 A, I 2 = UR R 2 = (12 V ) ( 6 Ω ) = 2 A,
Teil d) mit Gl. (25.11) P1 = UI1 = R1I12 = ( 4 Ω )( 3 A ) = 36 W, P2 = UI2 = R2 I22 = ( 6 Ω )( 4 A ) = 24 W,
2
2
Teil e) mit Gl. (25.12) P = IUQ = ( 5 A )(12 V ) = 60 W
Beispiel 25.10: In Reihe geschaltete Ohm'sche Widerstände
mögliches Prüfungsbeispiel
Universität Salzburg
Seite 12
09.04.2007
Musso: Physik II
Beispiel 25.11: Parallel- und Reihenschaltung Ohm'scher Widerstände
Teil 25 Gleichstromkreise
Seite 13
mögliches Prüfungsbeispiel
Beispiel 25.12: Eine komplizierte Schaltung Ohm'scher Widerstände
mögliches Prüfungsbeispiel
Universität Salzburg
Seite 13
09.04.2007
Musso: Physik II
Beispiel 25.13: Elektrogeräte in einem Stromkreis
Teil 25 Gleichstromkreise
Seite 14
Aufgenommene Leistungen von Elektrogertäten: Toaster Ptoaster = 900 W, Mikrowelle Pmikro = 1200 W,
Kaffeemaschine Pkaffee = 600 W, Stromkreis abgesichert mit Sicherung mit 10 A. Können alle Geräte
gleichzeitig betrieben werden?
Angeschlossene Geräte parallel betrieben, Spannung Unetz = 230 V ⇒
gesucht: Strom durch die einzelne Geräte, bzw. Gesamtstrom
aus Gl. (25.11) P = UI ⇒ Itoaster =
⇒
Ptoaster 900 W
P
P
1200 W
600 W
=
= 3.9 A, Imikro = mikro =
= 5.2 A, Ikaffee = kaffee =
= 2.6 A,
Unetz
230 V
Unetz
230 V
Unetz
230 V
durch Parallelschaltung ⇒ Gesamtstrom I = Itoaster + Imikro + Ikaffee = 3.9 A + 5.2 A + 2.6 A = 11.7 A ⇒
dieser Strom ist größer als die Angabe auf der Sicherung (10 A)
25.5 Die Kirchhoff'schen Regeln (Kirchhoff's rules)
Viele Stromkreise lassen sich nicht als Parallelschaltung oder
Reihenschaltung Ohm'scher Widerstände analysieren
Maschenregel
Knotenregel
Die erste Kirchhoff'sche Regel oder Maschenregel folgt aus der Anwesenheit
eines konservativen elektrischen Feldes:
∫ E ⋅ ds = 0 wobei C beliebiger
C
b
Zweite Kirchhoff'sche Regel
oder Knotenregel: I1 = I2 + I3
Universität Salzburg
geschlossener Weg ⇒ da ΔU = φb − φa = − ∫ E ⋅ ds ⇒ Summe der
a
Potentialänderungen entlang eines beliebigen geschlossenen Weg = 0
Seite 14
09.04.2007
Musso: Physik II
Stromkreis in einer Masche
Teil 25 Gleichstromkreise
Seite 15
Anwendung der Maschenregel: die Uhrzeigerrichtung
als positive Stromrichtung festgelegt ⇒
−IR1 − IR2 − UQ,2 − IRin,2 − IR3 + UQ,1 − IRin,1 = 0 ⇒
I=
UQ,1 − UQ,2
R1 + R2 + R3 + Rin,1 + Rin,2
Beispiel 25.14: Potentialdifferenz im Stromkreis
Gesucht: a) Potentiale in den Punkten a bis d, b) die Leistungsaufnahme und
Leistungsabgabe des Stromkreises ⇒
UQ,1 − UQ,2
Teil a) aus Gl. (25.25) I =
⇒
R1 + R2 + R3 + Rin,1 + Rin,2
12 V − 4 V
8V
=
= 0.5 A,
5 Ω + 5 Ω + 4 Ω + 1 Ω + 1 Ω 16 Ω
φa = φe + UQ,1 − IRin,1 = 0 V + 12 V − ( 0.5 A )(1 Ω ) = 11.5 V
I=
φb = φa − IR1 = 11.5 V − ( 0.5 A )( 5 Ω ) = 9.0 V, φc = φb − IR2 = 9.0 V − ( 0.5 A )( 5 Ω ) = 6.5 V,
φd = φc − UQ,2 − IRin,2 = 6.5 V − 4 V − ( 0.5 A )(1 Ω ) = 2.0 V
Teil b) von der Spannungsquelle 1 abgegebene Leistung:
PQ,1 = IUQ,1 = ( 0.5 A )(12 V ) = 6.0 W,
von der Widerständen umgesetzte Leistung:
PR = I 2 R1 + I 2 R2 + I 2 R3 + I 2 Rin,1 + I 2 Rin,2 = ( 0.5 A )
2
( 5 Ω + 5 Ω + 4 Ω + 1 Ω + 1 Ω ) = 4.0 W
von der Spannungsquelle zur Aufladung aufgenomm ene Leistung:
PQ,2 = IUQ,2 = ( 0.5 A )( 4 V ) = 2.0 W
Universität Salzburg
⇒ PQ,1 = PR + PQ,2
Masse
oder
Erde
Seite 15
09.04.2007
Musso: Physik II
Beispiel 25.15: Fremdstarten eines Autos
Teil 25 Gleichstromkreise
Seite 16
Starthilfe für ein Auto, dessen Akkumulator entladen ist:
a) Welche Pole des entladenen und des geladenen Akkumulators mit Hilfe von Fremtstartkabeln verbunden?
b) geladenes Akkumulator: UQ,1 = 12 V, Rin,1 = 0.02 Ω, entladenes Akkumulator UQ,2 = 11 V, Rin,2 = 0.02 Ω,
Fremdstartkabel R = 0.01 Ω ⇒ gesucht: Ladestrom
c) Akkus falsch angeschlossen ⇒ gesucht: Strom
Teil a) damit entladenes Akku wieder aufgeladen ⇒ durch diese ein Strom von positiven zum negativen Pol ⇒
gleichnamige Pole der Akkus verbinden!
UQ ,1 − UQ,2
12 V − 11 V
Teil b) aus Maschenregel: UQ,1 − IRin,1 − IRin,2 − UQ,2 − IR = 0 ⇒ I =
=
= 20 A
0.05 Ω
R + Rin,1 + Rin,2
Teil c) Akkus falsch angeschlossen ⇔ die Teilspannungen addieren sich ⇒ aus Maschenregel
UQ,1 − IRin,1 − IRin,2 + UQ,2 − IR = 0 ⇒ I =
UQ,1 + UQ,2
R + Rin,1 + Rin,2
=
12 V + 11 V
= 460 A
0.05 Ω
RICHTIG
gleichnamige Pole verbunden
Universität Salzburg
FALSCH!
Kurzschluß über R
Seite 16
09.04.2007
Musso: Physik II
Stromkreise mit mehreren Maschen
Teil 25 Gleichstromkreise
Seite 17
Die positive Stromrichtung kann
in jeder Masche willkürlich
festgelegt werden
Für Stromkreise mit mehr als eine Masche benötigt man beide Kirchhoff'sche Regeln.
φb − φa = −IR
UQ − RinI
Universität Salzburg
Seite 17
09.04.2007
Musso: Physik II
Beispiel 25.16: Anwendung der Kirchhoff'schen Regeln
Teil 25 Gleichstromkreise
Seite 18
mögliches Prüfungsbeispiel
Universität Salzburg
Seite 18
09.04.2007
Musso: Physik II
Beispiel 25.17: Ein Stromkreis mit drei Zweigen
Teil 25 Gleichstromkreise
Seite 19
mögliches Prüfungsbeispiel
Universität Salzburg
Seite 19
09.04.2007
Musso: Physik II
Meßgeräte für Strom, Spannung, und Widerstand
Teil 25 Gleichstromkreise
Seite 20
Strommessung mit einem Amperemeter
(in Reihe zu R geschaltet)
Spannungsmessung mit einem Voltmeter
(parallel zu R geschaltet)
Galvanometer
RS sehr groß, → ∞
RP sehr klein, → 0
Ein einfaches Ohmmeter ist eine Reihenschaltung
aus Spannungsquelle, einem Galvanometer, und
einem Widerstand RS (so gewählt, daß wenn a
und b kurzgeschlossen ⇒ Vollausschlag)
Universität Salzburg
Seite 20
09.04.2007
Musso: Physik II
25.6 RC-Stromkreise (RC circuits)
Teil 25 Gleichstromkreise
Seite 21
Eine Schaltung, die einen Ohm'schen Widerstand und einen Kondensator enthält, bezeichnet als
RC-Stromkreis. Der Strom fließt in einer Richtung, aber die Stromstärke ist zeitlich nicht konstant.
Entladen eines Kondensators
Q(t ) = Q0 e−t RC
exponentieller Abfall
Reihenschaltung eines Kondensators C, eines Schalters S und eines Widerstands R : Zum Zeitpunkt t ≤ 0 ⇒
obere Platte des Kondensators C enthält die Ladung + Q0 , die untere Platte - Q0 ⇒ Potentialdifferenz zwischen
U
Q0
Q
. Zum Zeitpunkt t = 0 Schalter geschlossen ⇒ Anfangsstrom I0 = C ,0 = 0 ⇒
RC
C
R
dQ
mit der Zeit nimmt die Ladung des Kondensators ab: I = −
⇒ Kirchhoff'sche Maschenregel UC − IR = 0 ⇒
dt
Q'
t'
Q dQ
Q
Q'
t'
dQ
dQ
dt
dQ
1
∼ −Q ⇒
R =0 ⇒
+
=−
=−
⇒ ∫
=−
dt ⇒ ln
=−
⇒
∫
C dt
RC
Q
RC
Q
RC
Q
RC
dt
0
Q0
0
den Platten UC ,0 =
da t ' beliebig gewählt ⇒ t ' = t
und Q ' = Q(t )
⇒ Q(t ) = Q0 e − t RC
Zeitkonstante τ : wie lange es dauert bis die Ladung
um den Faktor 1/ e = 0.37 abnimmt
Universität Salzburg
Seite 21
09.04.2007
Musso: Physik II
Teil 25 Gleichstromkreise
Seite 22
aus Q(t ) = Q0 e− t RC mit Gl. (25.27) I = −
dQ
dt
Q
⎛ Q ⎞
⇒ I = − ⎜ − 0 ⎟ e −t RC = 0 e −t RC
RC
⎝ RC ⎠
⇒
mit Gl. (25.26) I = I0 e−t RC
I (t ) = I0 e−t RC
exponentieller Abfall
Beispiel 25.18: Entladung eines Kondensators
Kondensator mit C = 4 μF, aufgeladen auf UC ,0 = 24 V, wird entladen über Widerstand mit R = 200 Ω ⇒
Gesucht: a) Anfangsladung q0 , b) Anfangsstrom I0 , c) Zeitkonstante τ = RC, d) Ladung nach t = 4 ms nach Schließen
der Verbindung Kondensator - Widerstand.
q
a) aus Gl. (24.6) C =
⇒ q0 = CUC ,0 = ( 4 μF )( 24 V ) = 96 μ C
U
U
24 V
b) aus Gl. (25.26) I0 = C ,0 =
= 0.12 A
200 Ω
R
c) aus Gl. (25.32) τ = RC = ( 200 Ω )( 4 μF ) = 800 μ s = 0.8 ms
d) aus Gl. (25.31) q(t ) = q0 e −t RC
Universität Salzburg
⇒ q(t = 4 ms) = ( 96 μ C ) e
− ( 4 ms ) ( 0.8 ms )
Seite 22
= ( 96 μ C ) e −5 = 0.647 μ C
09.04.2007
Musso: Physik II
Aufladen eeines Kondensators
Teil 25 Gleichstromkreise
Seite 23
Reihenschaltung einer Spannungsquelle U, eines Kondensators C, eines Schalters S und eines Widerstands R :
Zum Zeitpunkt t ≤ 0 ⇒ Kondensator entladen ⇒ Potentialdifferenz zwischen den Platten UC ,0 = 0.
Zum Zeitpunkt t = 0 Schalter geschlossen ⇒ Anfangsstrom I0 =
U
R
⇒
Q
Q
dQ
dQ
= 0 ⇒ mit I =
U−
R− =0 ⇒
C
C
dt
dt
Q'
t'
dQ
1
dQ
dt
=
=
⇒ ∫
dt ⇒
CU − Q RC
CU − Q RC ∫0
0
Kirchhoff'sche Maschenregel U − IR − UC = 0 ⇒ U − IR −
CU − RC
dQ
−Q = 0 ⇒
dt
RC
dQ
= CU − Q ⇒
dt
Q'
Substitution CU − Q = q und dq = −dQ ⇒
⇒ da t ' beliebig gewählt ⇒ t ' = t
⇒ CU − Q(t ) = CUe−t RC
Strom aus I =
⇒
dQ
∫0 CU − Q = −
und Q ' = Q( t )
(
Q(t ) = CU 1 − e−t RC
)
⇒
CU −Q '
∫
CU
dq
CU − Q '
t'
= ln
=−
q
CU
RC
CU − Q(t )
= e −t RC
CU
dQ
⎛ −1 −t RC ⎞ U −t RC
⇒ I = CU ⎜ −
e
= e
= I0 e −t RC
⎟
dt
⎝ RC
⎠ R
Universität Salzburg
Seite 23
09.04.2007
Musso: Physik II
Beispiel 25.19: Aufladung eines Kondensators
Teil 25 Gleichstromkreise
Seite 24
Mit einer Batterie U = 6 V wird ein Kondensator C = 2 μF über einen Ohm'schen Widerstand R = 100 Ω
augeladen. Gesucht: a) Strom I0 , b) Maximale Ladung des Kondensators qE = CU, c) die Zeit t zur Aufladung
auf 0.9 qE , d) die Ladung q für I = I0 / 2
⇒
Teil a) aus Gl. (25.37) I0 = U / R = ( 6 V ) / (100 Ω ) = 0.06 A
Teil b) aus Gl. (25.36) qE = CU = ( 2 μF )( 6 V ) = 12 μ C
(
Teil c) aus Gl. (25.36) q = CU 1 − e − t / RC
⇒
)
(
⇒ 0.9CU = CU 1 − e − t / RC
)
⇒
0.9 = 1 − e − t / RC
⇒ e− t / RC = 0.1
− t / RC = ln ( 0.1) = −2.30 ⇒ t = 2.30 RC = 2.30 (100 Ω )( 2 μF ) = 460 μ s
Teil d) aus Maschenregel U − RI − q / C = 0
U / 2 − q /C = 0
⇒
mit I = I0 / 2 = U / ( 2R )
⇒ U − RU / ( 2R ) − q / C = 0
⇒
q = (CU ) / 2 = qE / 2
Beispiel 25.20: Ströme und Ladungen nach verschiedenen Zeiten
Universität Salzburg
⇒
mögliches Prüfungsbeispiel
Seite 24
09.04.2007
Musso: Physik II
Die Energiebilanz beim Aufladen eines Kondensators
Teil 25 Gleichstromkreise
Während des Aufladens fließt durch die Batterie insgesamt qE = CU
Seite 25
⇒
die Batterie verrichtet die
Arbeit W = qEU = CU 2
Die Hälfte ist in Form von elektrischer Energie im Kondensator gespeichert (siehe Gl. 24.12)
1
qEU
2
Die andere Hälfte wird durch den Ohm'schen Widerstand in Wärme umgewandelt:
dWR
Rate, mit der Arbeit am Ohm'schen Widerstand R in Wärme umgewandelt wird
= RI 2
dt
Eel =
U
mit Gl. (25.37) I = e− t / RC
R
2
dWR
U 2 −2t / RC
⎛ U − t / RC ⎞
⇒
= R⎜ e
⇒
e
⎟ =
R
dt
⎝R
⎠
∞
Integration von t = 0 bis t = ∞ ⇒ WR =
∞
∞
U 2 −2t / RC
U2
t
d =
e −2t / RC dt
∫0 R e
∫
R 0
U2
U 2 e− at
− at
Substitution a = 2 / RC ⇒ WR =
e dt =
R ∫0
R −a
Universität Salzburg
⇒
∞
0
U 2 ( 0 − 1) U 2 U 2 RC 1 2
1
=
=
=
= U C = qEU
R −a
Ra
2R
2
2
Seite 25
09.04.2007
Musso: Physik II
Universität Salzburg
Teil 25 Gleichstromkreise
Seite 26
Seite 26
09.04.2007
Musso: Physik II
Teil 25 Gleichstromkreise
Seite 27
24. Elektrische Ströme
24.1 Einführung
Teil A: Elektrische Ströme und elektrische Felder
24.2 Elektrischer Strom
24.3 Das Ohm'sche Gesetz
24.4 Leitung
24.5 Elektrische Leistung
24.6 Kombinationen von Widerständen
24.7 Gleichstromschaltungen
24.8 Methoden zur Stromberechung in einem elektrischen Netzwerk
Teil B: Elektrische Ströme und magnetische Felder
24.9 Magnetische Kraft auf eine elektrische Ladung
24.10 Magnetisches Drehmoment auf einem elektrischen Strom
24.11 Von einem Strom erzeugtes magnetisches Feld
24.12 Magnetfeld eines geradliniges Stromes
24.13 Magnetfeld eines kreisförmiges Stromes
24.14 Kräfte zwischen elektrische Ströme
Universität Salzburg
Seite 27
09.04.2007