KM_I_2

Kristallstruktur und Mikrostruktur
Teil I
Vorlesung 2
1
Kristallstruktur und Mikrostruktur
Teil I
Scripte
http://www.uni-stuttgart.de/mawi/aktuelles_lehrangebot/Lehrangebot.html
2
Wiederholung
Koordinatensysteme
Ist das ein kristallographisches Koordinatensystem?
3
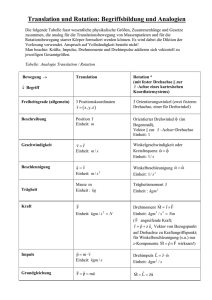
Wiederholung
Beschreiben die Metrik-Tensoren g und g* vollständig
eines Gitter?
g* =
x2
0
0
0
x2
0
0
0
y2
; x ≠ y
a* = x; b* = x, c* = y; a* = 90o; ß* = 90o; g* = 90o
V* = a*b*c* = x2y
a = b*c*sing*/V* = b*c*.1/V* = 1/x;
b = c*a*sinß*/V* = c*a*.1/V* = 1/x;
c = a*b*sina*/V* = a*b*.1/V* = 1/y;
a = b = 1/x ≠ c; c = 1/y; a = ß = g = 90o
 Tetragonales Gitter
4
Wiederholung
Quarz
Chemische Formel SiO2
Gitterparameter
a = 4.914 Å
c = 5.404 Å
b=? a=? ß=? g=?
Raumgruppe
P 3221 oder P3121 ?
Atom coordinates
Atom Multiplicity x/a
(Vielzahl)
Si
6c
0.4697
O
6c
0.4133
y/b
0
0.2672
z/c
0
0.1188
5
Teil I (Kristallographie)
1
Koordinatensysteme, Das Raumgitter, Das reziproke Gitter, Der Metrik-Tensor
2
Abstrakte Gruppen, Symmetrieelemente und Symmetrieoperationen,
Punktsymmetrie und Punktsymmetriegruppen
3
Translationssymmetrie, Transformationen des Gitters, Kombinationen von Translationen
und Punksymmetrieoperationen
4
1-, 2- und 3D Raumgruppen
5
Beispiele von Raumgruppen, Einfache Kristallstrukturen
5
Makroskopische physikalische Eigenschaften der Kristallen
Symmetrie – Invarianz gegenüber Transformationen
6
Geometrische Transformationen
Translationen
Punktsymmetrie Operationen
Vorlesung 2
Punktgruppen
Raumgruppen
Vorlesungen 3 und 4
Kristallstrukturen
Symmetrie von Molekülen
Äußerliche Symmetrie der Kristallen
Symmetrie der physikalischen Eigenschaften
7
Quarz
Punktgruppe 3 2
Nicht-zentrosymmetrische Gruppe
Morphologie
physikalische Eigenschaften
Piezoelektrizität
8
Was ist eine Gruppe?
‚Oktoberfest-Gruppe‘
Beispiel I (die ganze Zahlen)
… -4 -3 -2- -1 -0 1 2 3 4 …
1. m + n (2 + 3 = 5)
Abgeschlossenheit
2. (m + n) + p = m + (n + p); (2 + 3) + 5 = 2 + (3 + 5) Assoziativität
3. m + 0 = m; 2 + 0 = 2
Neutrales Element
4. m + n = 0; 2 + (-2) = 0
Invertierbarkeit
9
Beispiel II (Rotationen)
Rotation f = 120o
Rotation f2 = 240o
Rotation 1 ≡ 360o
1. Abgeschlossenheit f. f = f2 , f. f2 = 1
2. Assoziativität f. (f.f) = (f.f).f
3. Neutales Element (1) ist Rotation auf 360 Grad
4. Invertierbarkeit f. f2 = 1; (f )-1= f2 ; (f2 )-1= f
3 = {1, f, f2 } ; Punkgruppe 3
10
Abstrakte Gruppe - Definition
Gruppe G: Mathematische Struktur, besteht aus Elementen und Verknüpfungsregel (*)
1. Abgeschlossenheit:
für jedes Element A, B von G, C = A*B ist auch Element von G
2.  Neutrales Element E (1), E * A = A oder A * E = A
für jedes A von G
3. Inverses Element
für jedes A von G,  Inverses Element A-1 , A*A-1 = E
4. Assoziativität
A*(B*C) = (A*B)*C
11
‚Gruppentheorie‘
Ordnung der Gruppe │G│: die Zahl der Elementen in der Gruppe
(kann endlich oder unendlich sein)
Untergruppe U ≤ G: Teilmenge der Elementen von G die auch eine Gruppe
bezüglich der Verknüpfung von G ist.
Triviale Untergruppe: {E}
Abelsche Gruppe: Gruppe mit Kommutativgesetz A*B = B*A
Gruppe der ganzen Zahlen ( 2 + 3 = 3 + 2)
Niels H. Abel
12
Gruppentafel
Ordnung = 4
{E,A,B,C;*}
E
A
B
C
E
E
A
B
C
A
A
E
C
B
B
B
C
E
A
C
C
B
A
E
z.B. A*C=B
A-1 = A weil A*A=E
13
Gruppentafel
Beispiele
A=E
14
Punktsymmetrie Operationen
Drehachsen
Drehinversionsachsen
Punktsymmetriegruppen - die Gruppenelemente
sind
Punktsymmetrieoperationen
15
Drehachsen n
Drehwinkel für eine n-zählige Drehachse ist
fn = 360/n
(1)
kristallographische Drehachsen: n = 1, 2, 3, 4 oder 6!!!!
16
„Nichtkristallographische“ Drehachsen
5 Drehachse
102m
8 Drehachse
Ferrocene Molekül
17
Veranschaulichung der Nichtkompatibilität
„nichtkristallographischer“ Rotationen mit Translationssymmetrie
3
6
5
4
7
8
18
Drehachse 2
Drehwinkel:
180 Grad
Neutrales Element E (1): 360 Grad Drehung
Ordnung der Gruppe:
2
Graphisches Symbol der Achse:
Untergruppen:
Inverses Element:
2; 22 =1
Granat-Almadin
2
3
4
1
Gruppentafel
2
1
2
1
1
2
2
2
1
19
Cl
37
20
Drehachse 3
Granat-Almadin
Drehwinkel:
120 Grad
Neutrales Element E (1): 360 Grad Drehung
Ordnung der Gruppe:
3
Graphisches Symbol der Achse:
Untergruppen:
Gruppentafel
3
1
31
32
1
1
31
32
31
31
32
1
32
32
1
31
21
Drehachse 4
Granat-Almadin
Drehwinkel:
90 Grad
Neutrales Element E (1): 360 Grad
Ordnug der Gruppe:
4
Graphisches Symbol der Achse:
Untergruppen:
{2}
42 = 2
Gruppentafel
4
1
41
42
43
1
1
41
42
43
41
41
42
43
1
42
42
43
1
41
22
Drehachse 6
Drehwinkel:
60 Grad
Neutrales Element E (1): 360 Grad Drehung
Ordnung der Gruppe:
6
Graphisches Symbol der Achse:
Untergruppen:
{2}; {3}
Kombinationen von Symmetrieoperationen
62 = 3; 64 = 32
23
Zyklische Gruppen
Zyklische Gruppen – Jedes Element Gk eine Potenz
von Erzeugerelement f ist
Gk = fk , k = 0, 1, …|G|-1 ; |G| - Ordnung der Gruppe
Gl (2a)
{G} = {1, f, f2 , f3 , … fG-1 }
Inverses Element: (Gk )-1 = f-k
Abelsche Gruppen - fmfn = fn fm = fm+n
Gl (2b)
Gl (2c)
Drehachse n
Erzeugerelement fn = 360/n
{2} = {1,f2}
{3} = {1, f3, f32}
{4} = {1, f4, f42, f43}
{6} = {1, f6, f62, f63, f64, f65}
24
Drehinversionsachsen n
Drehwinkel für eine n-zählige Drehinversionsachse ist fn = 360/n.
Gl. (3)
Kombinierte Symmetrieoperationen = Drehung * Punktspiegelung (Inversion)
Kristallographische Drehinversionsachsen: n = 1, 2, 3, 4 und 6!!!!
Inversionszentrum
Spiegelebene
Abb 138 aus Müller
25
Drehinversionsachse 1
Inversionszentrum
Ordnung der Gruppe:
2
Graphisches Symbol der Achse:
MnSiO3
o
Untergruppen:
2
Gruppentafel
1
1
1
1
1
1
1
1
1
1
26
Drehinversionsachse 2
Spiegelebene (m)
Gips
Drehwinkel:
180o
Neutrales Element E (1): 360 Grad Drehung
Ordnung der Gruppe:
2
Graphiscges Symbol der Achse:
Untergruppen:
Inverses Element von m: m (m*m = 1)
H2O
Gruppentafel
O
1H
H
m
m
1
m
1
1
m
m
m
1
2
27
Drehinversionsachse 3
Drehwinkel:
120o
Neutrales Element E (1): 360 Grad Drehung
Ordnung der Gruppe:
6
Graphisches Symbol der Achse:
Untergruppen:
{1}; {3}
C
C
Zyklische Gruppe
Gk = (3)k
Ethane C2H6
28
Drehinversionsachse 4
Drehwinkel:
90o
Neutrales Element E (1): 360 Grad Drehung
Ordnung der Gruppe:
4
Graphisches Symbol der Achse:
Untergruppen:
{2}
( 4 )2 = 2
1
3
CCl4
Zyklische Gruppe
Gk = (4)k
4
2
29
Drehinversionsachse 6
Drehwinkel:
60o
Neutrales Element E (1): 360 Grad Drehung
Ordnung der Gruppe:
6
Graphisches Symbol der Achse:
Untergruppen:
{3}; {m}
2
1*
1
Zyklische Gruppe
H3BO3
Gk = ( 6 )k
3
30
Drehachsen - Zusammenfassung
Inversionszentrum
31
Erzeugende Symmetrieelemente
n
2
n/m
2/m
n2
nm
n/m m
3
4
6
32
2mm
6/mmm
32
Erzeugende Symmetrieelemente
2=m
nm
3
4
6
3m
33
Punktgruppe 2/m
Oxalsäure
C2O4H2
Erzeugende Elemente:
Ordnung der Gruppe:
2 und m
4
Untergruppen:
{1},{2};{m}
1 = 2/m
Gruppentafel
2/m
1
1
1
1
1
2
m
1
1
2
m
2
m
1
m
2
2
m
1
m
2
1
1
1
34
2/m
35
Punktgruppe 3 2
Erzeugende Elemente:
Ordnung der Gruppe:
3 und 2
6
Untergruppen:
{2};{3}
Drehachsen 2, 2‘ und 2‘‘ sind senkrecht auf
der 3 Achse.
2‘‘= Rotaion von 2 auf 120 Grad
2‘‘
2‘
36
32
37
Punktgruppe 2mm
z
H2O
O
2 und mIIx
4
Untergruppen:
{2};{m}
y
H
x
Erzeugende Elemente:
Ordnung der Gruppe:
H
mIIy = mIIx * 2
m
Gruppentafel
2mm
1
2IIz
mIIx
mIIy
1
1
2IIz
mIIx
mIIy
2IIz
2IIz
1
mIIy
mIIx
mIIx
mIIx
mIIy
1
2IIz
mIIy
mIIy
mIIx
2IIz
1
38
2mm
39
Punktgruppe 3 m
Erzeugende Elemente:
Ordnung der Gruppe:
3 + m II 3
12
Untergruppen:
{1}; {2}; {m}; {2/m}; {3}; {32}; {3m}
2= 3*m;
Ethane
2
m‘
m‘‘
40
3m
41
Punktgruppe 6/m m m
Erzeugende Elemente:
6 ; m ┴ 6; m || 6
Ordnung der Gruppe:
24
Untergruppen:
18[ {62m}; {6mm}; {622}; {6/m} …]
2
m‘ = 6* m || 6; 2= m ┴ 6 * m || 6
Benzene C6H6
m‘
m || 6
42
6/m m m
43
Punktgruppe
Erzeugende Elemente:
4; 3 und m
Ordnung der Gruppe:
48
m 3m ( 4 m 3 2 m )
SF6
3
Granat-Almadin
2
44
4
m3m
45
Punktgruppe Symbol
1 Symbol:
2 Symbole
3 Symbole
Kurze Form
3
2/m
Lange Form
3
2/m
32
32
3m
3 2/m
2mm
2mm
m3m
4/m 3 2/m
s1
s2
s3
Rictung 1 Richtung2 Richtung 3
46
Die 32 Kristallographische Punktgruppen
mit ihren gängigen (Kurz-)Symbolen
222
32
422
622
2/m 2/m 2/m
2/m 3
4/m 2/m 2/m
6/m 2/m 2/m
4/m 3 2/m
47
Ordnung
der Punktgruppe
3 m (12)
32; 3m und 3 (6)
2/m (4)
48
Kristallographische Punktgruppen (Kristallklassen)
Punktgruppen
Kristallsystem
Blickrichtungen
1, 1
triklin
2, m, 2/m
monoklin
[010]
222, 2mm, mmm (2/m 2/m 2/m)
orthorhombisch
[100], [010], [001]
4, 4, 4/m
tetragonal
422, 4mm, 42m, 4/mmm (4/m 2/m 2/m)
[001], [100], [110]
3, 3
32, 3m, 3m (3 2/m)
[001], [100], [110] (hex)
trigonal
6, 6, 6/m
hexagonal
622, 6mm, 62m, 6/mmm (6/m 2/m 2/m)
[001], [100], [110]
23, m3 (2/m 3)
432, 43m, m3m (4/m 3 2/m
[100], [111], [110]
kubisch
49
Beispiele http://ruby.chemie.uni-freiburg.de/Vorlesung/symmetrie_2_5_1.html
Kristallformen
Vivanite (Mexico) 2/m
Pyrite FeS2 2/m 3
2
2
Mackayite (USA) 4/m 2/m 2/m
4
Garnet
4/m 3 2/m
m
50
Analytische Darstellung von Punktgruppen
x‘
y‘ = T
z‘
x
y
z
Z
Gl (4)
x‘ = T11x + T12y + T13z
x,y,z
Y
x‘,y‘,z‘
{G }
{T}
Gl. (5)
X
51
Drehmatrizen
Drehungen um die kartesischen Koordinatenachsen
Drehung um die Z-Achse um Winkel f
cos(f) -sin(f) 0
T(f) = -sin(f) cos(f) 0
0
0
1
Gl (6a)
Drehung um die X-Achse um Winkel f
1
T(f) = 0
0
0
0
cos(f) -sin(f)
-sin(f) cos(f)
Gl (6b)
Drehung um die Y-Achse um Winkel f
cos(f) 0 -sin(f)
T(f) = 0
1
0
-sin(f) 0 cos(f)
Gl (6c)
52
Analytische Darstellung von Punktgruppen
Beispiele
4-zählige Drehachse parallel zu Z; 4Z
f = 90o, Gl (6a)
T=
0 -1 0
1 0 0
0 0 1
Z
Y
X
Z
6-zählige Drehachse parallel zu Y; 6Y
f = 60o, Gl (6c)
Y
T=
0.5 -0.866 0
0
1
0
0.866 0.5 0
X
53
Analytische Darstellung von Punktgruppen
Inversionzentrum (0,0,0)
Ti =
-1 0 0
0 -1 0
0 0 -1
Gl (7)
Drehinversionsachsen
T = Ti * T(f)
Gl (8)
Spiegelebene m senkrecht auf der X Aches m = 1*2
f = 180o, von Gl. (7), Gl. (6b) und Gl. (8)
-1 0 0
T(m┴X) = 0 -1 0
0 0 -1
1 0 0
0 -1 0
0 0 -1
-1 0 0
= 0 1 0
0 0 1
Gl (9)
Kleber, S. 64
54