z - bz emme

Mathematische Grundlagen für die Weiterbildung
BM-Vorkurs
V01.05
Die folgenden Aufgaben stellen als Überblick die Grundlagen für einen erfolgreichen Start
im BM Vorkurs dar.
Es gelten der Stoff aus www.mathbu.ch 8+ resp. 9+.
Nr.
Thema / Exemplarische Aufgabe
Arithmetisches Rechnen / allgemeines Rechnen
A00
Benötigt wird ein Taschenrechner mit techn./wissenschaftlichen Funktionen
(Wurzelziehen, Potenzieren etc. Bsp. Texas TI -30
A01
Einteilung des Zahlenraums (der Zahlenstrahl):
 Menge der natürliche Zahlen
 Menge der ganzen Zahlen
 Menge der rationalen Zahlen
 Vorzeichenregeln (Differenz zwischen Vorzeichen u. Operationszeichen)
AL01
Lösungsbeispiele
Menge der natürlichen Zahlen (ohne Null): Symbol  ℕ = {1, 2, 3, 4, 5, 6, 7,
8,...}
Menge der natürlichen Zahlen (mit Null):
7,...}
Symbol  ℕ0 = {0, 1, 2, 3, 4, 5, 6,
Menge der ganzen Zahlen:
2,...}
Symbol  ℤ = {-4, -3, -2, -1, 0, 1,
Menge der rationalen Zahlen:
Symbol  ℚ
a
Das sind alle Brüche   , deren Zähler und Nenner aus ganzen Zahlen bestehen. Alle
b
ganzen Zahlen können durch 1 (ebenfalls ganze Zahl) geteilt werden, deswegen sind alle
ganzen Zahlen auch rationale Zahlen.
Vorzeichenregel (Grundrechenoperationen):
Vorzeichen sind das + (plus) und das – (minus) Zeichen. Operationszeichen sind das
Additions-, das Subtraktions-, das Multiplikations- und das Divisionszeichen.
A02
Grundrechenoperationen (arithmetische sowie einfache algebraische Aufgaben):
 Addition/Subtraktion mit Klammern und ohne Klammern
 Multiplikation / Division mit und ohne Klammern
 Erweitern / Kürzen von Brüchen
 Addition / Subtraktion von Brüchen
 Multiplizieren von Brüchen
 Division von Brüchen
AL02
Lösungsbeispiele
AU_Math_Grundlagen_Weiterbildung
Datum 02.09.2015
Seite 1 von 5
Mathematische Grundlagen für die Weiterbildung
BM-Vorkurs
Nr.
V01.05
Thema / Exemplarische Aufgabe
1.  123   23  100
2.  3z   4 z   z
3. 16a  3b  8c  5a   b  3c   21a  4b  5c
4. 11a  5a  3b  5b  4a  5b  10a  7b
5.
 2  3  4   5  120
6.
 2   4   5  6  240
7.
 5x   3 y   15xy
8.
3a  7  b   c  3ac  7c  bc
9.
 27
 9
3
10. 
 24
4
6
11. kgV (kleinstes gemeinsames Vielfaches) von: 4; 7; 28; = 28
12. ggT ( grösster gemeinsamer Teiler) von: 16; 24; 56; = 8
13.
5a 2a 4a 8a 11a




 1a  a
11 11 11 11 11
14.
3x 5 x 19 x


6
9
18
15.
3 5
15
5
 

4 9
36
12
16.
6ab
25  x  y 

 10a
5  x  y 
3b
17.
6 3
2
: 
 12 4
3
 9y 
18.  18 xy  :  
  6ax
 3a 
A03
Lineare Gleichungen lösen
AU_Math_Grundlagen_Weiterbildung
Datum 02.09.2015
Seite 2 von 5
Mathematische Grundlagen für die Weiterbildung
BM-Vorkurs
V01.05
Nr.
Thema / Exemplarische Aufgabe
 Einfache Gleichungen mit ganzen Zahlen und der Unbekannten x
 Einfache Gleichungen mit Brüchen und der Unbekannten x
AL03
Lösungsbeispiele (nach x auflösen)
1. 8x  43  5x  76  x =11
1
1
11
2. x  3  2
x=
4
4
2
6
5
8 5
x  x  2,4  
x x=4
3.
16
12
5 24
A04



AL04
Berechnung eines Jahreszins für ein Kapital und einen gegebenen Zinsfuss
Berechnung eines Monats- resp. Tageszins für ein Kapital einen gegebenen
Zinsfuss und dem entsprechenden Zeitraum.
Umstellen der Jahreszinsformel nach allen Grössen
Lösungsbeispiele
K = Kapital; Z = Zins; p = Zinsfuss; t = Laufzeit (Tage, Monate, Jahre)
Z
K  p t
100  360
Beispiel: berechnen Sie das Kapital für: Zins 108.-, Zinsfuss 3.5%, angelegt
während 110 Tagen.  Resultat: Kapital = 10098.70 CHF
A05.


AL05
Lösungsbeispiele
1. Runden auf zwei Stellen nach dem Komma 13.753566 = 13.75
2. Runden auf zwei Stellen nach dem Komma 13.759883 = 13.76
3. Runden auf zwei Stellen nach dem Komma 13.998433 = 14.00 =14
Runden von Zahlen
Umrechnen von Bruchzahlen in Dezimalzahlen und umgekehrt
5
 1.25
4
1
2. Umrechnen in einen Dezimalbruch  0.33
3
1. Umrechnen in ein Dezimalzahl
75 3

100 4
Darstellung grosser Zahlen (inkl. mit Taschenrechner)
3. Umrechnen in eine Bruchdarstellung 0.75 
A06.

AU_Math_Grundlagen_Weiterbildung
Datum 02.09.2015
Seite 3 von 5
Mathematische Grundlagen für die Weiterbildung
BM-Vorkurs
Nr.
AL06
V01.05
Thema / Exemplarische Aufgabe
Lösungsbeispiele:
1. 1′ 700′ 000′000 = 1,7 ∙ 109
2. 1,278 ∙ 104 = 12′780
Geometrie ( Grundkonstruktionen Planimetrie / Berechnung von
geometrischen Grundflächen, –Körpern)
G01



Grundkonstruktionen mit Zirkel und Lineal: Halbieren einer Strecke ̅̅̅̅
𝐴𝐵 ,
Halbieren eines Winkels, Konstruieren einer Senkrechten s auf eine Gerade
g (Normale)
Konstruieren eines 30° Winkels (Zirkel und Lineal)
Übertragen eines gegebenen Winkels (Zirkel und Lineal)
GL01
Lösungsbeispiele
1. Mittelsenkrechte auf ̅̅̅̅
𝐴𝐵 konstruieren
2. Winkelhalbierende von 𝛼, 𝛽 𝑜𝑑𝑒𝑟 𝛾, konstruieren
3. 60° Winkel mithilfe eines gleichseitigen Dreiecks konstruieren. Üeber
Winkelhalbierende 30° Winkel konstruieren
G02
Winkel
 Winkelarten kennen (spitze, rechte, stumpfe, gestreckte Winkel etc.)
 einfache Winkelberechnungen (z.B. bei Winkelpaaren, bei Dreiecken)
GL02
Lösungsbeispiele
1. Nebenwinkel berechnen (Ergänzung zu 1800)
2. Scheitelwinkel, Stufenwinkel berechnen.
3. In einem Dreieck ist 𝛼 = 73°, 𝛽 = 64° . Wie gross ist 𝛾 ?
G03
Satz des Pythagoras
 Berechnungen am rechtwinkligen Dreieck (Hypotenuse, Katheten)
 Umstellen der Formel nach allen Grössen
GL03
Lösungsbeispiele:
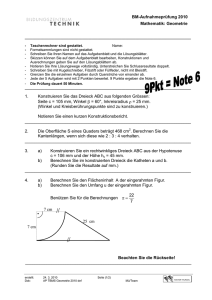
1. Ein im Punkt C rechtwinkliges Dreieck hat die Seitenlängen a = 5cm und
b = 4cm. Berechnen Sie die Länge der Seite c (Hypotenuse). 
𝑐 2 = 41𝑐𝑚2  𝑐 = √41𝑐𝑚2  𝑐 = 6,4𝑐𝑚
2. Berechnen Sie Kathete b eines rechtwinkligen Dreiecks. Kathete a =
7,8m, Hypotenuse c = 11m.  Kathete b ≈ 7,76m
G04
Einfache Flächenberechnungen und Umfangsberechnungen (mit Hilfe des
Formel-buches)
 Flächen- und Umfangsberechnungen: Quadrat, Rechteck, Parallelogramm,
Dreieck, Trapez und Kreis
AU_Math_Grundlagen_Weiterbildung
Datum 02.09.2015
Seite 4 von 5
Mathematische Grundlagen für die Weiterbildung
BM-Vorkurs
V01.05
Nr.
Thema / Exemplarische Aufgabe
GL04
Lösungsbeispiele
1. Berechnen Sie den Umfang und den Flächeninhalt von folgendem
Rechteck: Seite a = 11cm, Seite b = 8cm.  U = 38cm, A = 88cm2
2. Ein Rechteck hat einen Flächeninhalt von A = 216m2. Eine Seite ist 15cm
lang. Wie lang ist die andere Seite?  2. Seite = 14,4m
3. Berechnen Sie den Flächeninhalt von folgendem Dreieck: Grundseite c =
7cm, Höhe hc = 5cm.  A = 17,5cm2
4. Ein Trapez hat eine Fläche von 36mm2. Seite c = 12mm, Seite a = 6mm.
Berechnen Sie die Höhe h des Trapezes.  h = 4mm
5. Berechnen Sie den Umfang und Flächeninhalt des Kreises mit d = 2,80m
(d = Durchmesser).  U ≈ 8,80m, A ≈ 6,16m2
G05
Einfache Körperberechnungen (mit Hilfe des Formelbuches)
 Volumen und Oberfläche des Würfels
 Volumen und Oberfläche des Quaders
 Volumen und Oberfläche von Prismen. Mantelfläche eines Prismas
 Volumen und Oberfläche des Zylinders. Mantelfläche eines Zylinders
GL05
Lösungsbeispiele
1. Ein Würfel hat eine Kantenlänge von a = 2,8cm. Berechnen Sie die Oberfläche und das Volumen des Würfels.  O = 47,04m2, V = 21,952m3
2. Ein Quader hat folgende Kantenlängen: a = 5cm, b = 4cm, c = 9cm.
Berechnen Sie die Oberfläche des Quaders?  O = 202cm2
3. Ein Zylinder hat folgende Grössen: h = 12cm, r = 8cm. Berechnen Sie
das Volumen und die Mantelfläche?  V ≈ 2412,75cm3,
M≈
2
603,19cm
4. Ein Prisma hat eine quadratische Grundfläche mit Seitenlänge a = 8cm.
Berechnen Sie das Volumen des Prismas, wenn die Höhe 24cm beträgt.
 V = 1536cm3
AU_Math_Grundlagen_Weiterbildung
Datum 02.09.2015
Seite 5 von 5