Lösungen Überblick Dezimalbrüche

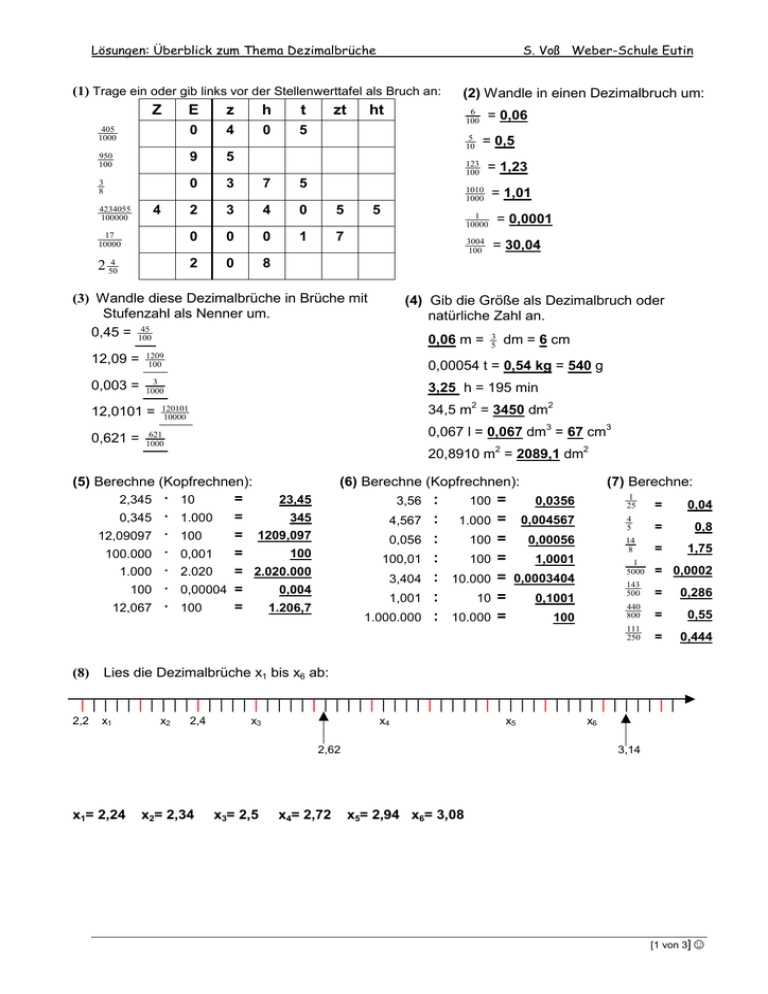
Lösungen: Überblick zum Thema Dezimalbrüche
S. Voß Weber-Schule Eutin
(1) Trage ein oder gib links vor der Stellenwerttafel als Bruch an:
Z
E
z
h
t
405
1000
0
4
0
5
950
100
9
5
3
8
0
3
7
5
2
3
4
0
5
17
10000
0
0
0
1
7
2 504
2
0
8
4234055
100000
4
zt
ht
6
100
5
10
= 0,06
= 0,5
123
100
= 1,23
1010
1000
5
= 1,01
1
10000
3004
100
(3) Wandle diese Dezimalbrüche in Brüche mit
Stufenzahl als Nenner um.
45
0,45 = 100
= 0,0001
= 30,04
(4) Gib die Größe als Dezimalbruch oder
natürliche Zahl an.
0,06 m =
3
5
dm = 6 cm
12,09 =
1209
100
0,00054 t = 0,54 kg = 540 g
0,003 =
3
1000
3,25 h = 195 min
12,0101 =
0,621 =
34,5 m2 = 3450 dm2
120101
10000
0,067 l = 0,067 dm3 = 67 cm3
621
1000
20,8910 m2 = 2089,1 dm2
(5) Berechne (Kopfrechnen):
=
23,45
2,345 10
=
345
0,345 1.000
= 1209,097
12,09097 100
=
100
100.000 0,001
=
2.020.000
1.000
2.020
0,004
100 0,00004 =
=
1.206,7
12,067 100
(8)
(2) Wandle in einen Dezimalbruch um:
(6) Berechne (Kopfrechnen):
3,56
4,567
0,056
100,01
3,404
1,001
1.000.000
(7) Berechne:
:
0,0356
100 =
: 1.000 = 0,004567
:
0,00056
100 =
:
1,0001
100 =
: 10.000 = 0,0003404
:
0,1001
10 =
: 10.000 =
100
1
25
=
0,04
4
5
=
0,8
14
8
=
1,75
1
5000
= 0,0002
143
500
=
0,286
440
800
=
0,55
111
250
=
0,444
Lies die Dezimalbrüche x1 bis x6 ab:
| | | | | | | | | | | | | | | | | | | | | | | | | | | | | | | | | | | | | | | | | | | | | | | | | | | |
2,2
x1
x2
2,4
x3
x4
2,62
x1= 2,24
x2= 2,34
x3= 2,5
x4= 2,72
x5
x6
3,14
x5= 2,94 x6= 3,08
[1 von 3]☺
Lösungen: Überblick zum Thema Dezimalbrüche
(9) Setze das entsprechende
Symbol ein (<; >; =):
3,01
4,55
3,089
1,10101
2,3232
0,0001
0,001
4,04
0,989
1,4
1
2,001
>
<
>
>
<
<
>
=
<
>
>
<
S. Voß Weber-Schule Eutin
(10) Runde auf die angegebene Stelle (G: Ganze, z: Zehntel...)
0,03 ≈ 0
G
3,001
4,555
3,0089
1,0101
3,2323
0,00099
0,0001
4,040
0,99
1,04
0,9999999
2,0099
+
+
+
+
+
+
0,0004 = 0,0004
t
2,33333 ≈ 2,333
zt
0,00049 ≈ 0,0005
h
3,4567 ≈ 3,46
h
0,071 ≈ 0,07
z
3,45 ≈ 3,5
t
4,09999 ≈ 4,1
0,123456 ≈ 0,1
z
h
0,40506 ≈ 0,41
G
G
0,801 ≈ 1
h
1,0101 ≈ 1,01
t
5,6
1,51
3,564
2,45
5,678 + 5,689
1,008 + 2,7071
=
=
=
=
=
=
2,345
3,091
9
25
= 11,725
= 52,547
= 0,81306
=
0,922
(16) Berechne:
3,66
1,6482
0,0252
1,23649
:
:
:
:
12,03 = 12,03
ht 2,0173411 ≈ 2,01734
2,3
2,67
2,4568
3,4
2,345
12,899
3,66
3,5265
0,0204
36,61
:
:
:
:
5
15
4
7
– 1,5
– 1,23
– 0,0579
– 0,7899
– 1,092 – 1,078
– 0,999 – 2,064
=
=
=
=
=
=
0,8
1,44
2,3989
2,6101
0,175
9,836
(15) Berechne:
(14) Berechne:
5
17
0,09034
0,03688
4,56 ≈ 5
(12) Subtrahiere (wenn möglich im Kopf):
9
8,21
7,2429
2,4556
13,707
7,1651
(13) Berechne:
2,07138 ≈ 2,0714
zt
(11) Addiere (wenn möglich im Kopf):
3,4
6,7
3,6789
0,0056
2,34
3,45
zt
2,345
3,091
0,9
25,25
=
0,732
= 0,2351
= 0,0051
5,23
=
3,4
0,01
0,09034
0,03688
=
7,973
= 0,03091
= 0,081306
= 0,93122
(17) Gib als Dezimalbruch an, dividiere entsprechend.
0,6
1,23
0,045
0,53
=
=
=
=
6,1
1,34
0,56
2,333
1
16
⇒
1 :
16 = 0,0625
3
45
⇒
3 :
45 = 0,0666... =
9
13
⇒
9 :
13 = 0,69230769....=
1
120
⇒
1 : 120 = 0,008333....=
3
16
⇒
3 :
14
25
⇒ 14 :
0,06
0,0083
16 = 0,1875
25 = 0,56
(18) Ordne diese Dezimalbrüche je einer der drei Dezimalbruchformen zu:
abbrechende Dezimalbrüche : 0,023
0,33333
1,45
0,00101
reinperiodisch Dezimalbrüche: 1,1
0,07
gemischt-periodische Dezimalbrüche: 0,01
4,2356
9,99
0,692307
0,001
0,25
1,1
8,84
2,2002
[2 von 3]☺
Lösungen: Überblick zum Thema Dezimalbrüche
(19) Forme um:
5
23
8 = 0,625
10 = 2,3
2
30
= 0,06
7
1000
2
3
= 0,007
= 0,6
6
25
= 0,24
S. Voß Weber-Schule Eutin
(20) Gib ohne Division an, welcher dieser Brüche
(21) Gib sofort den
einen abbrechenden, welcher einen periodischen
Dezimalbruch ergibt. Begründe Deine Aussage.
periodischen Dezimalbruch
bzw. Bruch an (ohne
Rechnung):
3
18
1
20
1
21
3 125 = 3,416
2
27
= 0,074
1
20
= 2⋅12⋅5 ⇒ nur Primfaktoren 2 oder 5 im Nenner,
also ist
1
21
1
20
ein abbr. DB.
= 31⋅7 ⇒ kein Primfaktor 2 oder 5 im Nenner,
4
9
1
90
= 0,4
0,7 =
= 0,01
0,03 =
0,1 =
1
9
2
3
7
9
1
30
= 0,6
also rein-periodisch.
3
1
1
18 = 6 = 2⋅3 ⇒ (mind.) einen Primfaktor 2 oder 5
und einen weiteren, anderen Primfaktor im Nenner,
also gemischt-periodisch.
(22) Sachaufgabe:
Die Mieter eines Mehrfamilienhauses müssen zukünftig mehr Nebenkosten zahlen. Die Abwasserkosten erhöhen sich
insgesamt um 125 € für alle 16 Mieter des Hauses, die Abfallkosten um 46,26 € pro Mieter und die zusätzlichen
Schneebeseitigungskosten von 41 € werden gleichmäßig auf 15 ungekündigte Mieter übertragen.
Runde sinnvoll und gib an, wie viel jeder der 15 ungekündigten Mieter monatlich zusätzlich zahlen muss.
125 € :16 = 7,8125 € ≈ 7,81 € 41 € : 15 =2,7 3 € ≈ 2,73 €
46,26 € +7,81 € + 2,73 € = 56,8 €
Jeder ungekündigte Mieter des Hauses muss zukünftig rund 56,80 € an Nebenkosten zusätzlich zahlen.
(23) Berechne:
a) x–3,45=0,394
b) 4,3–x = 2,87
x= 3,844
x= 1,43
c) 3,3x= 7,8+9,8
x= 5,3
d) 5,55 = x:2,24
e) 1,3 = 6,63 : x
x= 12,432
x= 6,63:1,3=5,1
(24) Berechne schrittweise untereinander:
4,1(3,23+5,032–(4,02:1,5):2)
= 4,1(32,768+5,032–(4,02:1,5):2)
= 4,1(32,768+5,032–2,68:2)
= 4,1(32,768+5,032–1,34)
= 4,1(37,8–1,34)
= 4,136,46
= 149,486
(25) Stelle einen Rechenterm /eine Gleichung auf und berechne:
a) Addiere zum Produkt von 3,4 und 1,11 die Differenz der Zahlen 4,5 und 0,11.
b) Das Produkt des Quotienten der beiden Zahlen 5,25 und 0,25 und einer unbekannten Zahl ergibt die
Differenz von 3,5 und 2,1.
a) (3,41,11)+(4,5–0,11) = 8,164
b) (5,25:0,25) x = 3,5–2,1
21 x = 1,4
x= 0 ,06
(26) Formuliere je eine Wortaufgabe:
a) 6,1 + 3,2 – 5,6 : 3,4
b) (x + 4,6) : 2,3 = 3,43,2
a) Bilde die Differenz der Summe aus 6,1 und 3,2 und dem Quotienten aus 5,6 und 3,4
b) Bildest du den Quotienten aus der Summe einer Zahl und 4,6 mit 2,3 , so erhältst du das Produkt
aus 3,4 und 3,2.
[3 von 3]☺