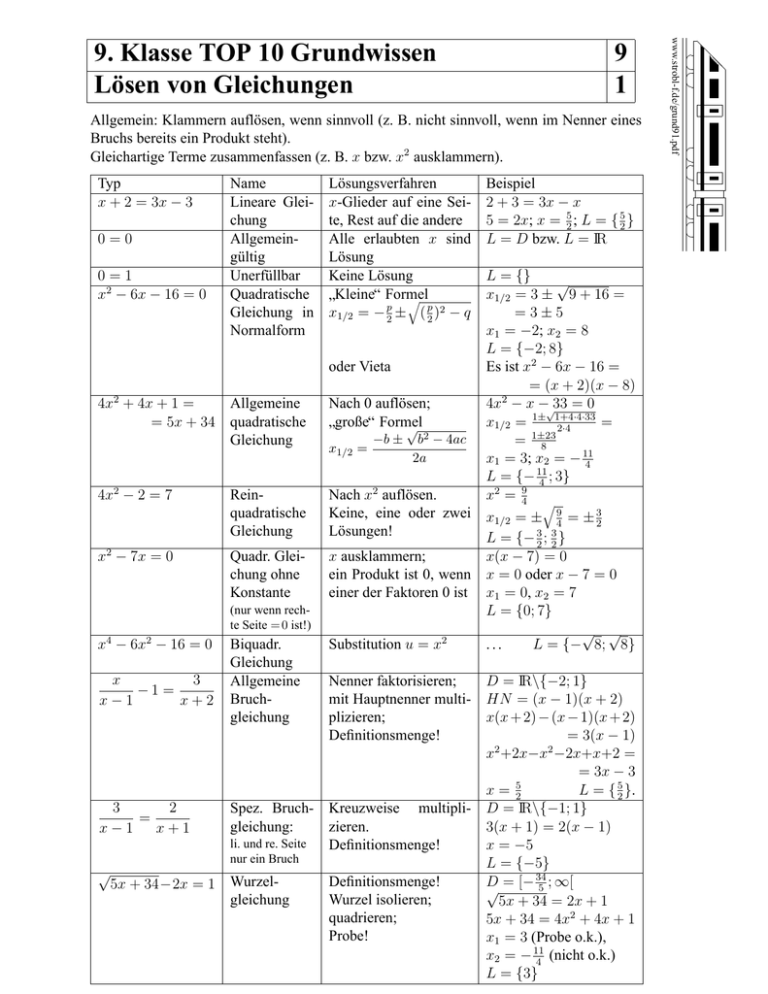
9. Klasse TOP 10 Grundwissen 9 L¨osen von Gleichungen 1

0=0
0=1
x2 − 6x − 16 = 0
Name
Lineare Gleichung
Allgemeingültig
Unerfüllbar
Quadratische
Gleichung in
Normalform
Lösungsverfahren
x-Glieder auf eine Seite, Rest auf die andere
Alle erlaubten x sind
Lösung
Keine Lösung
Kleine“ Formel
q
”
x1/2 = − p2 ± ( p2 )2 − q
oder Vieta
4x2 + 4x + 1 =
Allgemeine
= 5x + 34 quadratische
Gleichung
Nach 0 auflösen;
große“ Formel
√
”
2
4x2 − 2 = 7
Reinquadratische
Gleichung
Nach x2 auflösen.
Keine, eine oder zwei
Lösungen!
x2 − 7x = 0
Quadr. Gleichung ohne
Konstante
x ausklammern;
ein Produkt ist 0, wenn
einer der Faktoren 0 ist
x1/2 =
−b ±
b − 4ac
2a
(nur wenn rechte Seite = 0 ist!)
x4 − 6x2 − 16 = 0
x
3
−1 =
x−1
x+2
3
2
=
x−1
x+1
√
Biquadr.
Gleichung
Allgemeine
Bruchgleichung
Substitution u = x2
Spez. Bruchgleichung:
Kreuzweise multiplizieren.
Definitionsmenge!
li. und re. Seite
nur ein Bruch
5x + 34−2x = 1 Wurzelgleichung
Nenner faktorisieren;
mit Hauptnenner multiplizieren;
Definitionsmenge!
Definitionsmenge!
Wurzel isolieren;
quadrieren;
Probe!
Beispiel
2 + 3 = 3x − x
5 = 2x; x = 52 ; L = { 52 }
L = D bzw. L = IR
L = {}
√
x1/2 = 3 ± 9 + 16 =
=3±5
x1 = −2; x2 = 8
L = {−2; 8}
Es ist x2 − 6x − 16 =
= (x + 2)(x − 8)
2
4x − x −√33 = 0
x1/2 = 1± 1+4·4·33
=
2·4
1±23
= 8
x1 = 3; x2 = − 11
4
L = {− 11
; 3}
4
x2 = 94 q
x1/2 = ± 94 = ± 32
L = {− 32 ; 32 }
x(x − 7) = 0
x = 0 oder x − 7 = 0
x1 = 0, x2 = 7
L = {0; 7}
√ √
...
L = {− 8; 8}
D = IR\{−2; 1}
HN = (x − 1)(x + 2)
x(x + 2) − (x − 1)(x + 2)
= 3(x − 1)
2
2
x +2x−x −2x+x+2 =
= 3x − 3
5
x= 2
L = { 52 }.
D = IR\{−1; 1}
3(x + 1) = 2(x − 1)
x = −5
L = {−5}
D = [− 34
; ∞[
5
√
5x + 34 = 2x + 1
5x + 34 = 4x2 + 4x + 1
x1 = 3 (Probe o.k.),
x2 = − 11
(nicht o.k.)
4
L = {3}
Typ
x + 2 = 3x − 3
Allgemein: Klammern auflösen, wenn sinnvoll (z. B. nicht sinnvoll, wenn im Nenner eines
Bruchs bereits ein Produkt steht).
Gleichartige Terme zusammenfassen (z. B. x bzw. x2 ausklammern).
9
1
www.strobl-f.de/grund91.pdf
9. Klasse TOP 10 Grundwissen
Lösen von Gleichungen
ax2 + bx + c = 0
Sonderfälle mit fehlendem“ linearen Glied bx bzw. fehlender Konstante c → grund93.pdf.
”
Ist a = 1, lautet die Gleichung also x2 + bx + c = 0, spricht man von einer Gleichung in
Normalform.
Lösen quadratischer Gleichungen in Normalform x2 + bx + c = 0
Kleine Formel“:
v
!2
”
u
b u
b
x1/2 = − ± t
−c
2
2
(Bezeichnet man b als das Mittlere“ und c als das Hintere“, so könnte man für die kleine Formel sagen:
”
”
Minus das Mittlere halbe plusminus Wurzel aus das gerade Hingeschriebene im Quadrat minus das Hintere“.)
”
Beispiel:
x2 + 8x − 7 = 0
( Das Mittlere“ ist 8, also das Mittlere halbieren und mit anderem Vorzeichen hinschreiben: −4; plusminus
”
Wurzel schreiben; darunter das Quadrat davon: 16; das Hintere“ ist −7, also mit anderem Vorzeichen noch
”
unter die Wurzel schreiben: +7):
x1/2 = −4 ±
√
16 + 7 = −4 ±
√
23
Ist der Wert unter der Wurzel 0, so hat man nur eine Lösung (sog. doppelte Lösung).
Ist der Wert unter der Wurzel negativ, so kennzeichnet man dies als verbotenen Ausdruck;
die quadratische Gleichung hat dann keine Lösung.
Lösen allgemeiner quadratischer Gleichungen ax2 + bx + c = 0
Falls die Gleichung bequem durch a dividiert werden kann, kann man sie in Normalform
bringen und wie oben beschrieben lösen. Andernfalls verwendet man die Mitternachtsfor”
mel“ (sie ist so wichtig, dass man sie auch mitten in der Nacht auswendig wissen muss):
√
−b ± b2 − 4ac
x1/2 =
2a
Beispiel: 4x2 − 14x − 30 = 0
√
+14± 196−4·4·(−30)
x1/2 =
= 14±26
; x1 = 5; x2 = −1,5
2·4
8
Für Wurzeln mit Radikand 0 oder negativem Radikanden gilt das oben gesagte analog.
Zahl der Lösungen
Ist man nur an der Anzahl der Lösungen interessiert, betrachtet man nur den Ausdruck unter
der Wurzel, die sog. Diskriminante D = b2 − 4ac. Ist D positiv, so hat die gegebene quadratische Gleichung zwei Lösungen, ist D = 0, so gibt es eine doppelte Lösung, und ist D
negativ, so gibt es keine Lösung.
Beispiele:
−5x2 + 6x − 80 = 0: D = b2 − 4ac = 62 − 4 · (−5) · (−80) < 0, also keine Lösung.
5x2 − 40x + 80 = 0: D = b2 − 4ac = (−40)2 − 4 · 5 · 80 = 0, also eine doppelte Lösung,
nämlich (mit Formel nachrechnen!) x1/2 = 4
Erster Schritt
Quadratische Gleichungen löst man meist, indem man zuerst alles auf eine Seite bringt,
also die Gleichung auf die folgende Form bringt:
Zum Lösen quadratischer Gleichungen gibt es verschiedene Möglichkeiten. Bei der hier gegebenen Vorgehensweise wird ein bestimmtes Verfahren favorisiert. Varianten → grund93.pdf.
9
02
www.strobl-f.de/grund92.pdf
9. Klasse TOP 10 Grundwissen
Quadratische Gleichungen
Quadratische Gleichungen — Sonderfälle
• Fehlt“ das lineare Glied bx, so handelt es sich um eine reinquadratische Gleichung.
”
Man löst die Gleichung nach x2 auf, d. h. bringt die x2 -Stücke auf die eine, die Konstante auf die andere Seite.
Beim anschließenden Ziehen der Wurzel beachte man: Ist die rechte Seite positiv, so gibt
es zwei Lösungen (±), ist sie 0, so gibt es
eine doppelte Lösung, und ist sie negativ, so
gibt es keine Lösung.
Beispiele:
; x1/2 = ± 52
4x2 − 25 = 0; x2 = 25
4
2 2
x = 0; x2 = 0; x1/2 = 0
3
5x2 + 125 = 0; x2 = −25; L = {}
• Biquadratische Gleichungen
So heißen Gleichungen, die nur x4 - und x2 -Stücke sowie Konstanten enthalten. Man
löst sie durch Substitution, indem man x2 durch einen anderen Variablen-Buchstaben
ersetzt (z. B. x2 = u, dann ist x4 = u2 ), wodurch eine quadratische Gleichung entsteht. Beispiel:
x4 − 8x2 − 20 = 0
Substitution x2 = u:
u1/2
u2 − 8u − 20 = 0
√
= 4 ± 16 + 20; u1 = 10;
u2 = −2
Nach Lösung der quadratischen Gleichung folgt eine Rücksubstitution, indem der
gewählte Variablen-Buchstabe wieder durch x2 ersetzt wird. Die dann vorliegenden
reinquadratischen Gleichungen haben je nach rechter Seite keine, eine oder zwei Lösungen, sodass eine biquadratische Gleichung insgesamt null bis vier Lösungen haben
kann. In obigem Beispiel ergeben sich zwei Lösungen:
x1/2
x2 = 10 oder x2 = −2
√
pp
= ± 10 bzw. pp p ?
Varianten zum Lösen quadratischer Gleichungen
• Die Mitternachtsformel kann auch geschrieben werden als x1/2 =
1
2a (−b
±
√
b2 − 4ac).
• Die Verwendung der Mitternachtsformel ist auch bei Normalform möglich, wenn man a = 1 setzt.
Beispiel: x2 + 8x − 7 = 0
p
√
√
√
√
1
x1/2 = 2·1
(−8± 64 − 4 · 1 · (−7)) = 12 (−8± 92) = −4± 12 4 · 23 = −4± 12 ·2· 23 = −4± 23
• Satz von Vieta: → grund96.pdf
• Quadratische Ergänzung:
Hier wird die quadratische Gleichung auf Normalform gebracht und eine binomische Formel erzeugt.
Beispiel:
2x2 + 16x − 14 = 0 | : 2
x2 + 8x − 7 = 0
2
x + 8x + 16 − 16 − 7 = 0
(x + 4)2 = 23
√
√
x + 4 = + 23 oder x + 4 = − 23
√
√
x1 = −4 + 23; x2 = −4 − 23
Beispiel:
4x2 − 14x = 0
x(4x − 14) = 0
x = 0 oder 4x − 14 = 0
x1 = 0; x2 = 14
= 72
4
• Fehlt“, nachdem alles auf eine Seite gebracht wurde,
”
die Konstante c, so klammert man x aus. Das dabei entstehende Produkt ist 0, falls einer der Faktoren 0 ist, also
falls x = 0 ist oder der verbleibende Klammerausdruck
0 ist.
9
03
www.strobl-f.de/grund93.pdf
9. Klasse TOP 10 Grundwissen
Quadratische Gleichungen: Sonderfälle
(denn für x muss um d weniger eingesetzt werden, um den gleichen Funktionswert zu erhalten, der sich ohne d ergäbe).
Die Graphen quadratischer Funktionen sind Parabeln (→ grund95.pdf); der tiefste bzw.
höchste Punkt heißt Scheitel.
Ist a > 0, so ist die Parabel nach oben geöffnet ( ), bei a < 0 nach unten ( ).
Ist a = 1 oder a = −1, so kann man sie beim üblichen Koordinatensystem (1 cm für eine
Längeneinheit) auch mit der Schablone zeichnen.
Bei |a| > 1 ist die Parabel enger ( ), bei |a| < 1 weiter ( ).
Bestimmung des Scheitels mit quadratischer Ergänzung
Beispiel 1
Beispiel 2
Beispiel 3
1 2
2
y = x + 6x + 6
y = 2x − x + 2
y = −2x2 + 8x − 3
1. Schritt: a ausklammern (zum Ausgleich in der Klammer durch a dividieren, in Beispiel 2
also geteilt durch 12 , d. h. mal 2):
y = 12 [x2 − 2x + 4]
y = −2[x2 + 4x + 32 ]
2. Schritt: Durch Halbierung des Koeffizienten des linearen Gliedes eine binomische Formel
schreiben, Platz lassen für 3. Schritt:
y = (x + 3)2 . . . + 6
y = 12 [(x − 1)2 . . . + 4] y = −2[(x − 2)2 . . . + 32 ]
3. Schritt: Quadriert man die binomische Formel zur Kontrolle aus, so erhält man außer dem
gewünschten linearen Glied noch zusätzlich ein Quadrat, das oben nicht dasteht und mit
minus wieder ausgeglichen werden muss:
y = (x + 3)2 − 9 + 6 y = 12 [(x − 1)2 − 1 + 4] y = −2[(x−2)2 −4+ 32 ]
4. Schritt: Zusammenfassen und äußere Klammer wieder ausmultiplizieren:
y = (x + 3)2 − 3
y = 12 (x − 1)2 + 32
y = −2(x − 2)2 + 5
5. Schritt: Angabe des Scheitels: Aus den Werten d und e der Funktionsgleichung y = a(x +
d)2 + e erkennt man (siehe oben), dass es sich um eine verschobene Parabel handelt, und
zwar um e nach oben und um d nach links, so dass der Scheitel bei (−d|e) liegt:
S(−3| − 3)
S(1|1,5)
S(2|5)
Alternative zur quadratischen Ergänzung:
Man bestimmt die Nullstellen (Schnittstellen des Graphen mit der x-Achse, sofern solche
vorhanden sind), indem
man den Funktionsterm gleich 0 setzt: ax2 +bx+c = 0; die Lösungs√
2
b
formel (x1/2 = −b± 2ab −4ac ) liefert dann symmetrisch links und rechts von − 2a
liegende
Nullstellen, so dass wegen der Achsensymmetrie der Parabel in der Mitte der Nullstellen bei
b
x = − 2a
der Scheitel liegt. Den y-Wert erhält man durch Einsetzen in die Funktionsgleichung.
Beispiel: y = x2 + 6x + 6.
√
Nullstellen (→ grund92.pdf): x1/2 = −3 ± 3. Also ist der Scheitel bei x = −3.
y-Wert: x = −3 einsetzen in y = x2 + 6x + 6 liefert y = −3. Also S(−3| − 3).
y = c, und der Punkt (0|c) ist dann der
Schnittpunkt mit der y-Achse).
Die Funktionsgleichung kann auf verschiedene Arten gegeben sein, z. B.
y = ax2 + bx + c
y = a(x + d)2 + e
a bestimmt die Form des Funktionsgraphen (siehe unten).
bx nennt man auch lineares Glied, e bewirkt eine Verschiebung des Graphen nach oben
c Konstante.
(bzw. bei negativem e nach unten)
c ist in der Zeichnung des Graphen (denn in einer Wertetabelle sind dann alle y-Werte um e größer).
d bewirkt eine Verschiebung nach links (bzw. bei neder y-Achsenabschnitt
(denn setzt man x = 0 ein, so ergibt sich gativem d nach rechts)
9
04
www.strobl-f.de/grund94.pdf
9. Klasse TOP 10 Grundwissen
Quadratische Funktionen: Scheitel
Nullstellen
Beispiel 2
y = 12 x2 − x + 2
S2 (1|1,5) √
Beispiel 3
y = −2x2 + 8x − 3
S3 (2|5)
√
x1/2 =
x1/2 =
x1 ≈ −1,3, x2 ≈ −4,7
keine Nullstellen
x1 ≈ 0,4, x2 ≈ 3,6
(0|2)
(0| − 3)
y-Achsenschnitt (0|6)
1±
1−4· 12 ·2
2· 12
−8±
Scheitel
Beispiel 1
y = x2 + 6x + 6
S1 (−3| − 3)
√
x1/2 = −3 ± 3
64−4·(−2)·(−3)
2·(−2)
Würde die Funktionsgleichung y = x2 lauten, so erhielte man für die x-Werte ±1, ±2, ±3
die Funktionswerte 1, 4, 9.
Für die Funktionsgleichung y = 12 x2 müsste man diese Werte mit 12 multiplizieren und
erhielte 12 , 2, 92 ; für y = −2x2 entsprechend die Werte −2, −8, −18.
Da die Parabeln der obigen Beispiele durch Verschiebung aus den eben genannten hervorgehen, kann man nun ausgehend vom Scheitel Parabelpunkte finden:
In Beispiel 1 geht man vom Scheitel 1 (bzw. 2 bzw. 3) Einheiten nach links/rechts und 1
(bzw. 4 bzw. 9) Einheiten nach oben (siehe Zeichnung).
In Beispiel 3 geht man vom Scheitel 1 (bzw. 2 bzw. 3) Einheiten nach links/rechts und 2
(bzw. 8 bzw. 18) Einheiten nach unten.
y6
r
r
r
Durch die Punkte legt man
dann eine glatte Kurve (insSr 3
besondere im Scheitel nicht
Beispiel 2
spitz, sondern rund!):
r
T
r
r
r
r
r
r
r
r
S2
r
1
6
r
r r
Beispiel 1
r
Sr1
r
r
0
r
-r
2 nach rechts
r
-
x
1
r
4
nach
roben
Beispiel 3
r
Zur Zeichnung der Parabel bestimmt man zunächst den Scheitel, die Nullstellen (falls vorhanden) und den Schnittpunkt mit der y-Achse (→ grund94.pdf).
9
05
www.strobl-f.de/grund95.pdf
9. Klasse TOP 10 Grundwissen
Quadratische Funktionen: Zeichnung
r
Schnittpunkte
zweier Funktionsgraphen berechnet man durch Gleichsetzen der Funktionsterme. So ist für
den Schnittpunkt von Beispiel 1 und Beispiel 2 zu rechnen: x2 + 6x + 6 = 12 x2 − x + 2.
√
Diese Gleichung hat die Lösungen (→ grund92.pdf) x1/2 = −7 ± 41, also x1 ≈ −0, 60,
x2 ≈ −13, 42.
Die y-Werte
erhält man durch Einsetzen in eine der beiden Funktionsgleichungen: y1/2 =
√
54 ∓ 41, also y1 ≈ 2,78, y2 ≈ 105,22 (siehe Zeichnung Punkt T ).
Satz von Vieta
Quadratische Ungleichungen
Bequem ist meist folgendes Verfahren:
1. Man löse zunächst die quadratische Ungl. nach 0 auf, d. h. bringe alles auf eine Seite.
2. Man bestimme die Lösungen der zugehörigen quadratischen Gleichung.
3. Man denke sich den Graphen der zugehörigen quadratischen Funktion (Nach oben
oder nach unten geöffnet? Die gerade berechneten Lösungen sind die Nullstellen!)
4. Man bestimme mit Hilfe einer Grobskizze die Lösungsmenge der Ungleichung.
Beispiele:
x2 + 2x > 143
x2 + 2x − 143 > 0
Die zugehörige qu. Gl. x2 +
2x − 143 = 0 hat die Lösungen x1 = −13, x2 = 11.
Zum Term x2 + 2x − 143
gehört eine nach oben geöffnete Parabel mit Nullstellen
−13 und 11:
x2 + 4x ≤ 0
Die zugehörige qu. Gleichung x2 + 4x = 0 hat die
Lösungen x1 = −4, x2 = 0.
Zum Term x2 +4x gehört eine nach oben geöffnete Parabel mit Nullstellen −4 und
0:
−4
−13
0
-
-
11
Gesucht sind in obiger Ungleichung die x-Werte, für
die die Funktionswerte x2 +
2x−143 > 0 sind, also oberhalb der x-Achse sind.
Der Skizze entnimmt man:
L =] − ∞; −13[∪]11; ∞[
−4x2 + 8x − 20 < 0
Die zugehörige qu. Gleichung −4x2 + 8x − 20 = 0
hat keine Lösungen.
Zum Term −4x2 + 8x −
20 gehört eine nach unten
geöffnete Parabel ohne Nullstellen:
Gesucht sind in obiger Ungleichung die x-Werte, für
die die Funktionswerte x2 +
4x ≤ 0 sind, also unterhalb
(oder auf) der x-Achse sind.
Der Skizze entnimmt man:
L = [−4; 0]
Gesucht sind in obiger
Ungleichung die x-Werte,
für die die Funktionswerte
−4x2 + 8x − 20 < 0 sind,
also unterhalb der x-Achse
sind.
Der Skizze entnimmt man
nun, dass dies für alle xWerte der Fall ist: L = IR
Wichtig ist das umgekehrte Faktorisieren:
Hat man für die quadratische Gleichung ax2 + bx + c = 0 z. B. mit der Formel die Lösungen
x1 = r und x2 = s gefunden, so ist ax2 + bx + c = a(x − r)(x − s) ( x minus Lösung“).
2 +5x−24
”
Dies kann z. B. zum Kürzen von Bruchtermen verwendet werden. Beispiel: 5xx2 +80x+320
Zähler: x2 +5x−24 = 0 liefert x1 = 3, x2 = −8 und damit x2 +5x−24 = (x−3)(x−(−8));
Nenner: 5x2 + 80x + 320 = 0 liefert x1/2 = −8 (doppelte Lösung), also 5x2 + 40x + 80 =
5(x − (−8))(x − (−8)) = 5(x + 8)2 .
2 +5x−24
x−3
Insgesamt: 5xx2 +80x+320
= (x−3)(x+8)
= 5(x+8)
5(x+8)2
Gelingt es, eine in Normalform gegebene quadratische Gleichung x2 +bx+c = 0 auf die Form (x−r)(x−s) =
0 zu bringen, so sind x1 = r und x2 = s die Lösungen der Gleichung (denn ein Produkt ist 0, wenn einer der
Faktoren 0 ist).
Bei umgekehrtem Ausmultiplizieren erkennt man: (x − r)(x − s) = x2 − sx − rx + rs = x2 − (s + r)x + rs.
Also ist (1) die Konstante c = rs das Produkt der zwei Lösungen und
(2) b = −(r + s) die negative Summe der zwei Lösungen.
Mit diesem Vorwissen kann man manchmal die Lösungen schnell sehen.
Beispiel: x2 − 5x − 14 = 0. Da −14 nur auf vier Arten als Produkt natürlicher Zahlen darstellbar ist (nämlich
(−14) · 1, 14 · (−1), (−7) · 2 und 7 · (−2)), und nur eine davon die Eigenschaft (2) hat, nämlich 7 + (−2) = 5,
sind x1 = 7 und x2 = −2 Lösungen der quadratischen Gleichung.
9
06
www.strobl-f.de/grund96.pdf
9. Klasse TOP 10 Grundwissen
Satz von Vieta. Quadratische Ungleichungen
Erste Lösungsschritte
Zunächst wird wieder alles auf eine Seite gebracht, dann die Variable x (bzw. x2 ) ausgeklammert:
x2 + x2 − ax − x + 18 = 0
2x2 − (a + 1)x + 18 = 0
Zur Anwendung von Formeln, die man sonst für die quadratische Gleichung ax2 +bx+c = 0
hat, muss man sich hier jetzt
für a die 2 denken,
für b den Ausdruck −(a + 1),
für c die 18.
Anzahl der Lösungen
Die Diskriminante D = b2 − 4ac“ lautet hier:
”
D = [−(a + 1)]2 − 4 · 2 · 18 = (a + 1)2 − 144 = a2 + 2a + 1 − 144 = a2 + 2a − 143
Nun gilt:
(2) Ist a2 + 2a − 143 > 0, so hat die Gleichung (1) zwei Lösungen.
(3) Ist a2 + 2a − 143 < 0, so hat die Gleichung (1) keine Lösung.
(4) Ist a2 + 2a − 143 = 0, so hat die Gleichung (1) eine Lösung.
(An dieser Stelle muss man die Diskriminante a2 + 2a − 143 und die zu lösende Gleichung (1) x2 − ax + 18 =
x − x2 auseinanderhalten).
Löst man die Ungleichung a2 + 2a − 143 > 0 (→ grund96.pdf), so kann man genauer
angeben:
(2) Für a < −13 und a > 11 hat (1) zwei Lösungen.
(3) Für −13 < a < 11 hat (1) keine Lösung.
(4) Für a = −13 und a = 11 hat (1) eine Lösung
Setzt man nämlich a = −13 in (1) ein, so entsteht x2 + 13x + 18 = x − x2 mit der einen Lösung x1/2 = −3.
Setzt man a = 11 ein, so ensteht x2 − 11x + 18 = x − x2 mit der einen Lösung x1/2 = 3 (nachrechnen!).
Lösungen der Gleichung (1)
Sofern der Parameter a so ist, dass eine √
Lösung existiert (siehe voriger Abschnitt), so erhält
−b± b2 −4ac
“:
man mit der Lösungsformel x1/2 =
2a
”
q
√
+(a + 1) ± (a + 1)2 − 4 · 2 · 18
a + 1 ± a2 + 2a − 143
x1/2 =
=
2·2
4
Hinweis: Die Formeln stehen hier in Anführungszeichen, da das Formel-a nicht mit dem Parameter a verwechselt werden darf.
Zur Bedeutung des Parameters:
Zu unterscheiden sind hier die Variable x, nach der aufgelöst werden soll, und der Parameter
a, der für eine Zahl steht.
Ist z. B. a = 19, so hat man die Gleichung x2 − 19x + 18 = x − x2 (mit der Lösungsmenge
L = {1; 9});
ist a = 3, so hat man die Gleichung x2 − 3x + 18 = x − x2 (mit der Lösungsmenge L = {}).
Die Lösungsmenge hängt also vom Parameter a ab.
x2 − ax + 18 = x − x2
Beispiel:
(1)
9
07
www.strobl-f.de/grund97.pdf
9. Klasse TOP 10 Grundwissen
Quadratische Gleichungen mit Parameter
x2
− 6x + 9 =
q
(x −
3)2
= |x − 3| =
• Definitionsbereich:
(
x−3
für x ≥ 3
−x + 3 für x < 3
(Wurzelgleichungen → grund91.pdf)
Unter der Wurzel darf nichts Negatives stehen, d. h. der Radikand muss ≥ 0 sein.
√
Bei x muss also x ≥ 0 sein,
√
bei x2 − 4 muss x2 − 4 ≥ 0 sein, d. h. x ≥ 2 oder x ≤ −2,
bei
√1
x+5
muss x + 5 > 0 sein (wegen des Nenners hier > statt ≥), d. h. x > −5.
• Rechenregeln
Produkte und Quotienten/Brüche dürfen unter einer Wurzel zusammengefasst werden:
q
q
q
√
√
√
√ √
√
√
√ √
2
ab
b
√2 =
√ab =
2 · 3 = 2 · 3 = 6,
a · b = ab,
,
=
3
ac
ac
c
3
• Teilweise radizieren
Man sucht unter der Wurzel quadratische Faktoren und zieht daraus die Wurzel:
√
√
√
32 = 16 · 2 = 4 2
√
√
√
ab2 c7 = ab2 c6 c = bc3 ac (für a, b, c ≥ 0, sonst |bc3 | mit Betrag!)
q
√
√
9x2 − 36 = 9(x2 − 4) = 3 x2 − 4 (keine weitere Vereinfachung möglich!)
Umgekehrt: Vor
Wurzel stehende
Faktoren werden quadratisch in die Wurzel hin√ der √
√
eingezogen: 3 7 = 9 · 7 = 63
• Rationalmachen des Nenners durch Erweitern:
√
√
√
√1 = √1· √3 = 3
(Erweitern
mit
3)
3
3
3· 3
√
√
√
√
√
√
14·7
2 14+7 2
2
7
√ 2
=
= 2 14+
=
=
−
14
−
2 (So erweitern, dass
4−7
3
3
22 − 7
die 3. binomische Formel [Plusminusformel] anwendbar ist).
√
14
√
2− 7
√
14(2+
7)
√
√
(2− 7)(2+ 7)
√
• Vorsicht: Man darf bei Summen oder Differenzen die Wurzeln nicht einzeln ziehen:
√
√
√
√
Beispiel: 25 − 16 ist nicht gleich 25 − 16 (links: 9 = 3, rechts: 5 − 4 = 1).
√
√
Sondern: Ausdrücke wie a2 − b2 oder c + d können nicht vereinfacht werden.
• Vorsicht: Man darf nicht in eine Wurzel hineinkürzen:
√
√
Beispiel: 212 ist nicht 6.
√
√
√
√
3
Sondern: Teilweise radizieren, falls möglich: 212 = 24·3 = 2·q
= 3, oder den
2
√
√
√
Nenner quadratisch in die Wurzel hineinziehen: 212 = 12 12 = 14 · 12 = 3.
√
• Das Wurzelziehen (Radizieren) ist die Umkehrung des Quadrierens. Daher ist z. B.
√
√
√ 2 √ √
25 = 52 = 5
und
5 = 5 · 5 = 5.
q
√
√
√
Da sowohl (−3)2 = 9 = 3 als auch 32 = 9 = 3, muss man bei Variablen,
√
deren Vorzeichen nicht bekannt ist, Betragsstriche setzen: a2 = |a|, ebenso z. B. bei
Anwendung einer binomischen Formel (Beträge → grund85.pdf):
9
08
www.strobl-f.de/grund98.pdf
9. Klasse TOP 10 Grundwissen
Wurzeln
Wichtige Anwendungen:
• Auflösen der Formel a2 + b2 = c2 nach c bzw. a:
√
√
c = a2 + b 2
a = c2 − b2
(Diese Ausdrücke können nicht weiter vereinfacht werden und sind insbesondere nicht gleich a + b
bzw. c − b)
• Die rechtwinkligen Dreiecke in verschiedenen Lagen erkennen:
Dreht man obiges Dreieck, so erkennt man leicht neben A = 12 chc
eine weitere Formel für die Fläche des Dreiecks: A = 12 ab
c b
• Anwendung in der Physik:
t
S
SFN s
FG
S
w
S
F
H
=
?
a
In der nebenstehenden Abbildung sind r⊥s, FH kt,
FN ⊥t und FG ⊥r.
Im großen äußeren Dreieck gilt r2 + s2 = t2 .
Im kleinen inneren Dreieck ist FN ⊥FH und daher
FG2 = FN2 + FH2 .
r
• Durch Einzeichnen von Hilfslinien rechtwinklige Dreiecke erzeugen:
Beispiel (Abbildung links):
Gegeben sind der Kreisradius r = 5,3 m und J
J
der Abstand a = 2,8 m. Gesucht ist q.
J
J
Lösung (Abbildung rechts):
J r
p
Man zeichnet die punktierte Hilfslinie der
J
r
J
Länge a ein und erhält damit ein rechtwinkliges
√
J
2
2
2
2 − a2 =
Dreieck
mit
p
+
a
=
r
,
also
p
=
r
J
q
J
a
2
2
J
(5,3 m) − (2,8 m) = 4,5 m.
q Damit ist q = r − p = 0,8 m.
q
q
a
a
• Diagonale im Quadrat
• Höhe im gleichseitigen Dreieck
T
2
2
2
d = a +√
a
h2 + ( a2 )q2 = a2
Ta
√
a
2
d
h T
⇒ d = 2a
⇒ h = a2 − a4 = 23 a
aT
2 T
a
J
J
J
J
J r
J
r
J
J
J
J
J
• Diagonale im Quader
H
2
a2
2
2
B
Betrachte zunächst ∆ABD: Dort ist DB = + b .
2
Betrachte dann ∆HDB: Dort ist HB = DB + h2 .
2
Also ist HB = a2 + b2 + h2 .
B
B
h B
D
• Abstand der Punkte P1 (x1 |y1 ) und P2 (x2 |y2 ):
P1 P2 =
q
(x2 − x1 )2 + (y2 − y1 )2
b
A
B
B
@ B
@B
@B B
a
c
a2 + b 2 = c 2
(die Hypotenuse liegt dem rechten Winkel gegenüber).
Satz von Pythagoras:
In einem rechtwinkligen Dreieck mit den Katheten a, b und
der Hypotenuse c gilt
S
S a
S
S
S
S
S
b
9
09
www.strobl-f.de/grund99.pdf
9. Klasse TOP 10 Grundwissen
Pythagoras
S
SS
Für die Ähnlichkeit von Dreiecken genügt eines der folgenden Merkmale:
• Lauter gleiche Winkel
• Lauter gleiche Streckenverhältnisse
• Ein gemeinsamer Winkel und ein gemeinsames Streckenverhältnis, und zwar das Verhältnis der Seiten, die diesen Winkel einschließen (oder von zwei anderen Seiten, sofern die größere Seite dem Winkel gegenüber liegt).
Beispiele:
• Ein rechtwinkliges Dreieck wird durch die Höhe auf der Hypotenuse in zwei Teildreiecke zerlegt. Dann ist jedes der Teildreiecke zum ganzen Dreieck ähnlich:
C
∆F BC ∼ ∆ABC
Begründung: Die Dreiecke haben beide einen rechten
Winkel und den gemeinsamen Winkel β, sind daher ähnlich.
Also stimmen auch die entsprechenden Streckenverhältnisse überein.
S
S
S
βS B
F
A
im ∆F BC
BC
FC
FB
Dabei
entsprechen die nebenstehenden Seiten
einander:
im ∆ABC
AB
AC
BC
dem rechten Winkel gegenüber
dem Winkel β gegenüber
an beiden Winkeln anliegend
Also kann man z. B. folgendes Streckenverhältnis bilden:
BC
FB
=
AB
BC
2
Nach kreuzweiser Multiplikation folgt: BC = AB · F B.
• Strahlensatz V-Figur
Strahlensatz X-Figur
B0
Ist ABkA0 B 0 , so ist
∆ZAB ∼ ∆ZA0 B 0 , da
dann die Dreiecke lauter
gleiche Winkel haben.
A
B
A
A
A
A
A
A
A
Z
A0
A
Somit gelten:
ZA
ZB
=
ZA0
ZB 0
und
ZA
AB
=
ZA0
A0 B 0
B
!
!
!!
!
!
A0
!!
!
! Z
A
!!
B0
Streckungsfaktor m
In ählichen Figuren ist jede Strecke der Bildfigur m-mal so lang wie die entsprechende
Strecke der Originalfigur.
C0
S
A0 B 0 = m · AB usw.
0 S
C
m =2
h
Bei m > 1 erhält man eine Vergrößerung,
S
S
bei
0 < m < 1 eine Verkleinerung.
S
h S
0
0
A
SB
A
SB
Beachte: Flächeninhalte werden dabei mit dem Faktor m2 vergrößert:
A∆A0 B 0 C 0 = 12 A0 B 0 · h0 = 12 mAB · mh = m2 A∆ABC
Ähnliche Figuren sehen bis auf die Größe gleich aus. Sie haben gleiche Winkel und gleiche
Streckenverhältnisse. Bei der Betrachtung geometrischer Skizzen ist es meist hilfreich, sich
eine Teilfigur gestreckt ( aufgeblasen“) oder gestaucht ( geschrumpft“) zu denken und in
”
”
eine andere Teilfigur hineinzudrehen oder hineinzuspiegeln.
Schreibweise:
S
strecken
spiegeln
und
drehen
∆ABC ∼ ∆A0 B 0 C 0
9
10
www.strobl-f.de/grund910.pdf
9. Klasse TOP 10 Grundwissen
Ähnlichkeit. Strahlensatz. Streckung