Schulcurriculum Mathematik - Deutsche Internationale Schule

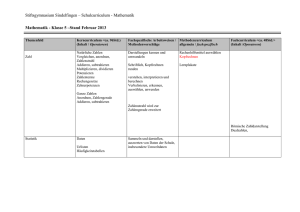
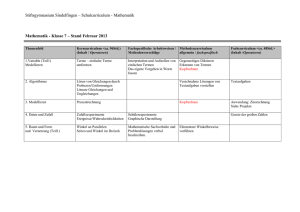
Schulcurriculum Mathematik
Stand: 03.06.2016
. 2016
Schulcurriculum
der
Deutschen Internationalen Schule Johannesburg
der Klasse 6
im Fach
Mathematik
Stand: 3.06.2016
Kl. 6 Curriculum Mathematik
Seite 1 von 4
Schulcurriculum Mathematik
Stand: 03.06.2016
. 2016
Mathematik 6
Die folgenden Standards im Fach Mathematik benennen sowohl allgemeine als auch inhaltsbezogene mathematische Kompetenzen, die Schülerinnen und
Schüler in aktiver Auseinandersetzung mit vielfältigen mathematischen Inhalten und Aufgabenstellungen im Unterricht erwerben sollen. Durch die Gestaltung
des Unterrichts erwerben die Schülerinnen und Schüler parallel zu den allgemeinen und den inhaltlichen mathematischen Kompetenzen auch methodischstrategische, sozial-kommunikative und personale Kompetenzen.
Bei den allgemeinen mathematischen Kompetenzen handelt es sich um
• mathematisch argumentieren
• Probleme mathematisch lösen
• mathematisch modellieren
• mathematische Darstellungen verwenden
• mit Mathematik symbolisch/formal/technisch umgehen
• kommunizieren über Mathematik und mithilfe der Mathematik
Der Bildungsplan 2016 des Bundeslandes Baden-Württemberg deckt 75% des vorliegenden schulinternen Curriculums. Typisch für Auslandschulen ist
allgemein die starke Heterogenität im Sprachniveau der Schüler in den DAM Klassen und im speziellen der Unterricht von DAF Klassen. Der schulspezifische
Teil (25%) ist daher zu einem Großteil durch Spracharbeit (DFU) abgedeckt. Weitere schulspezifische Ergänzungen und Vertiefungen sind an entsprechender
Stelle explizit ausgewiesen.
Für alle Schulen verbindliche Vereinbarungen
• Das Curriculum orientiert sich am Bildungsplan von Baden-Württemberg.
• Die zeitlichen Angaben im Curriculum stellen eine Orientierung dar.
• Alle Kompetenzen besitzen Operatoren, die einen messbaren Performanzanteil haben und können daher zur Überprüfung der
Lernergebnisse herangezogen werden.
• Die Leistungsbewertung erfolgt durch schriftliche Lernkontrollen und sonstige Kontrollen (mündlich, praktisch).
• Binnendifferenzierung erfolgt in Anlehnung an die Niveaustufen Grundstufe (G), Mittlere Stufe (M) und Erweiterungsstufe (E).
Kl. 6 Curriculum Mathematik
Seite 2 von 4
Schulcurriculum Mathematik
Stand: 03.06.2016
. 2016
Mathematik 6
Kompetenzen (mit Niveaustufen G, M, E)
Schülerinnen und Schüler können…
…Brüche in Dezimalzahlen (abbrechend oder periodisch)
und abbrechende Dezimalzahlen in Brüche
umwandeln(G,M,E),
… Brüche, Dezimalzahlen und Prozentangaben ineinander
umwandeln (G,M),
… einfache Rechnungen sicher im Kopf durchführen, unter
anderem, um Ergebnisse überschlägig zu
überprüfen(G;M),
… positive Dezimalzahlen schriftlich addieren,
subtrahieren, multiplizieren (dabei ein Faktor maximal 3stellig) und dividieren (Divisor maximal 2-stellig) (M,E),
… bei Division und Multiplikation von positiven
Dezimalzahlen Kommaverschiebungen anwenden und das
Verfahren begründen (M,E),
… situationsgerecht runden, gerundete Angaben
interpretieren und die Genauigkeit von Ergebnissen
bewerten(G,M,E),
… Rechnungen unter Verwendung der Umkehroperation
überprüfen (G,M),
... Sachsituationen durch Zahlterme beschreiben (G,M,E),
… Fachbegriffe verwenden (G),
… Rechengesetze für Rechnenvorteile nutzen (M,E)
Inhalte
6.1
Rechnen mit Bruchzahlen
Zeit
Schulspezifische
Ergänzungen
10 W
ð Ma 5
(gebrochene
Zahlen)
Wiederholung Erweitern, Kürzen,
Addieren und Subtrahieren,
Vervielfachen und Teilen von
Bruchzahlen,
Anmerkungen/
Quellen
Diff:
mit Variablen
arbeiten
Multiplikation und Division von
Bruchzahlen,
Rechengesetze,
Vergleich der Zahlbereiche N und Q+
Dezimale Schreibweise,
Vergleichen, Ordnen und Runden,
Diagramme,
Addieren und Subtrahieren,
Multiplizieren und Dividieren,
abbrechende und periodische
Dezimalbrüche
Kl. 6 Curriculum Mathematik
Seite 3 von 4
Schulcurriculum Mathematik
Kompetenzen (mit Niveaustufen G, M, E)
Schülerinnen und Schüler können…
… Winkelweiten schätzen und messen (G,M),
… alltagsbezogene Representanten als Schätzhilfe
verwenden (G),
… rechte, spitze, stumpfe Winkel identifizieren (G), mithilfe
eines Geodreiecks Winkel vorgegebener Winkelweite und
Höhen im Dreieck zeichnen (G),
… mit Größenangaben rechnen (G),
… den Umfang von Dreiecken bestimmen (G),
… rechtwinklige, spitzwinklige, gleichschenklige und
gleichseitige Dreiecke identifizieren (G),
... Sachsituationen durch Zahlterme beschreiben (M,E)
Stand: 03.06.2016
Inhalte
6.2.
Geometrische Figuren
Kl. 6 Curriculum Mathematik
5W
Begriffe am Kreis,
Winkelarten,
Winkel vergleichen, schätzen, messen
und zeichnen,
besondere Winkel – Kreisausschnitt,
Dreiecksarten
Zuordnungen – Dreisatz
… einfache Zusammenhänge zwischen Zahlen oder Größen
Erkennen und beschreiben (G,M);
… Punkte in ein Koordinatensystem eintragen und die
Koordinaten von Punkten ablesen (G),
… einfache funktionale Zusammenhänge in verbaler,
tabellarischer und graphischer Form (auch im
Koordinatensystem) darstellen und zwischen den
Darstellungsformen wechseln (G,M,E),
… proportionale und antiproportionale Zusammenhänge in
konkreten Situationen erkennen und Sachprobleme mit
dem Dreisatz in der Je-desto- Form lösen (G,M)
Zeit
Schulspezifische
Ergänzungen
Dynamische
Geometriesoftware
Anmerkungen/
Quellen
ð Kommunikationsfähigkeit
mathematische
Fachsprache,
Argumentieren
Quotientengleichheit,
Produktgleichheit
5W
Tabelle und Graph einer Zuordnung,
ð Phy, Geo (Bewegungen,
Klima)
proportionale Zuordnungen,
antiproportionale Zuordnungen,
ð Ma 7 (lineare Funktionen)
Dreisatz bei proportionalen und
antiproportionalen Zuordnungen
Seite 4 von 4
Schulcurriculum Mathematik
Kompetenzen (mit Niveaustufen G, M, E)
Schülerinnen und Schüler können…
Stand: 03.06.2016
Inhalte
… zu einer statistischen Fragestellung eine Datenerhebung
planen und durchführen (G,M),
… Daten aus vorgegebenen Sekundärquellen entnehmen
(G,M),
… absolute und relative Häufigkeiten (auch in Prozent)
bestimmen (G,M),
… Daten grafisch darstellen, auch unter Verwendung von
Tabellenkalkulation und aus solchen Darstellungen
Zahlenwerte ablesen (G,M,E),
… die Kenngrößen Maximum, Minimum, Mittelwert
bestimmen (G),
… mithilfe der Kenngrößen von Daten statistische Aussagen
formulieren (G,M,E),
… Daten aus ihrer Erfahrungswelt auch bei
unterschiedlichen Darstellungsformen auswerten,
vergleichen und bewerten (G,M,E),
… statistische Darstellungen hinsichtlich ihrer Eignung und
ihrer möglichen Irreführung beurteilen (G,M,E)
6.3.
Statistische Daten
… Kreise und Vierecke identifizieren und deren spezielle
Eigenschaften beschreiben (G,M),
… den Umfang von Trapez und Parallelogramm bestimmen
und beim Kreis mithilfe der Formel berechnen (G,M),
… die Formeln für den Flächeninhalt eines Parallelogramms
und eines Dreiecks geometrisch erklären(M,E),
… den Flächeninhalt von Parallelogramm, Trapez, Dreieck
und Kreis berechnen und von daraus zusammengesetzten
Figuren bestimmen (G,M,E),
… mithilfe eines Zirkels Kreise bei vorgegebenem Radius
bzw. Durchmesser zeichnen (G),
... Sachsituationen durch Zahlterme beschreiben (G,M,E)
Dreiecksarten und Vierecksarten
(Quadrat, Rechteck, Raute,
Parallelo-gramm, Trapez)
Kl. 6 Curriculum Mathematik
Zeit
Schulspezifische
Ergänzungen
Anmerkungen/Quellen
ð einfache Zufallsversuche,
Arbeit mit Quellen wie
Lexika, Zeitschriften,
Jahrbücher, Internet
4W
Statistische Erhebung mit Urliste,
Strichliste, Häufigkeitstabelle
ð Geo, Bio
Tabellenkalkulation
absolute und relative Häufigkeiten,
Maximum, Minimum,
Mittelwert/arithmetisches Mittel
Balken-, Säulen-, Streifen- und
Kreisdiagramm
Figuren und Körper
Umfang und Flächeninhalt von
Parallelogramm, allgemeinem
Dreieck und Trapez
Systematisierung der Vierecke
Flächeninhalt von Vielecken,
Umfang und Flächeninhalt eines
Kreises, krummlinige Flächen
ð Ma5 (Körper und Figuren)
6W
Diff.:
Drachenviereck,
Allaussagen,
Existenzaussagen,
„Wenn-dann-Form“
ð Sätze in
„Wenn …, dann …Form“
ð entdeckendes
anschauliches
Gewinnen von
Beziehungen,
ð Rückführprinzip
ð Kommunikationsfähigkeit
ð Methodenbewußtsein
Seite 5 von 4
Schulcurriculum Mathematik
Stand: 03.06.2016
6.4.
Rationale Zahlen – Terme
… rationale Zahlen und Punkte auf der Zahlengeraden
einander zuordnen, vergleichen, anordnen und die
Anordnung beschreiben (G,M),
… den Betrag einer Zahl angeben (G),
… erläutern, dass zwischen zwei rat. Zahlen stets beliebig
viele weitere rat. Zahlen liegen (M),
... einfache Rechnungen sicher im Kopf durchführen, unter
anderem, um Ergebnisse überschlägig zu überprüfen(G;M),
… rat. Zahlen in Bruch- und Dezimal-darstellung addieren,
subtrahieren, multiplizieren, dividieren (G,M,E)
… situationsgerecht runden, gerundete Angaben
interpretieren und die Genauigkeit von Ergebnissen
bewerten(G,M,E),
… Rechnungen unter Verwendung der Umkehroperation
überprüfen (G,M),
... Sachsituationen durch Zahlterme beschreiben (G,M,E),
… Fachbegriffe verwenden (G),
… Rechengesetze für Rechnenvorteile nutzen (M,E);
… den Wert von Zahltermen mit Klammern berechnen,
wobei rat. Zahlen nur in gleicher Darstellungsform auftreten
(M,E)
Kl. 6 Curriculum Mathematik
Begriff ganze und rationale Zahl
Ordnung der rationalen Zahlen,
negative und positive Zahlen,
Gegenzahl,
Zunahme und Abnahme,
Betrag einer Zahl
Erweiterung des
Koordinatensystems
Addition, Subtraktion,
Multiplikation, Division
10W
Diff:
mit Variablen
umgehen
und arbeiten;
Formeln aufstellen
und umstellen
ð Ma 5/6
(Zahlbereiche)
ð Geo; Bio
ð Einsatz eines
Taschenrechners
ð Unterschied zwischen
Rechenzeichen
(Operation) und
Vorzeichen
Rechengesetze
Systematik der Zahlbereiche N,Q+,
Q und Z
Seite 6 von 4
Schulcurriculum Mathematik
Operatoren
Stand: 03.06.2016
Zuordnung zu Anforderungsbereichen
Operatoren müssen in einen Bezug zu Anforderungsbereichen gestellt werden. In der Praxis ist die Zuordnung jedoch vom Kontext von Aufgabenstellungen und
ihrer unterrichtlichen Einordnung abhängig. Dies hat zur Folge, dass eine eindeutige Zuordnung zu nur einem Anforderungsbereich eigentlich nicht möglich ist.
Diese Übersicht ordnet dennoch jeden Operator einem einzigen Anforderungsbereich nach folgenden Überlegungen zu: In diesem Anforderungsbereich wird
der Operator erfahrungsgemäß überwiegend genutzt beziehungsweise die präzisierende Beschreibung des Operators führt zur gewählten Zuordnung.
Die Anforderungsbereiche beschreiben nicht unbedingt ein Anspruchsniveau, es kann zum Beispiel ein Operator aus dem Anforderungsbereich III auch in
kognitiv einfacheren Zusammenhängen verwendet werden.
Operatoren in den Bildungsstandards Mathematik
In der Beschreibung der Kompetenzen dienen die Operatoren zur Präzisierung der Anforderungen. Konsequentes Wahrnehmen und Einhalten der mithilfe von
Operatoren gemachten Vorgaben trägt dazu bei, dass einerseits das vorgesehene Niveau erreicht wird und andererseits eine Überinterpretation der Standards
und der damit verbundene Mehraufwand an Unterrichtszeit vermieden werden.
Vollständigkeit der Auflistung
Verben wie lösen, differenzieren werden hier nicht beschrieben, da ihre Bedeutung unmissverständlich ist. Die Bedeutung und der zuzuordnende
Anforderungsbereich vieler Verben (wie zum Beispiel formulieren, planen, nutzen, umgehen) ergeben sich in der Regel aus dem Kontext. Dies gilt genau
genommen auch für die ausgewählten Operatoren in der Übersicht. Die explizite Beschreibung dient jedoch einer Präzisierung des Verständnisses dieser
Operatoren und trägt zu ihrer einheitlichen Nutzung auch in Aufgabenstellungen bei.
Kl. 6 Curriculum Mathematik
Seite 7 von 4
Schulcurriculum Mathematik
Stand: 03.06.2016
Anforderungsbereich I
Umfasst das Wiedergeben von Sachverhalten und Kenntnissen im gelernten Zusammenhang, die Verständnissicherung sowie das Anwenden und
Beschreiben geübter Arbeitstechniken und Verfahren
angeben, nennen
Ergebnisse numerisch oder verbal formulieren, ohne Darstellung des Lösungsweges und ohne
Begründungen
berechnen
Ergebnisse von einem Ansatz oder einer Formel ausgehend durch Rechenoperationen gewinnen
zeichnen,
grafisch darstellen
Anfertigen einer zeichengenauen, grafischen Darstellung auf der Basis der genauen Wiedergabe wesentlicher Punkte
beziehungsweise maßgetreues oder maßstäbliches zeichnerisches Darstellen eines Objekts
Anforderungsbereich II
Umfasst das selbstständige Auswählen, Anordnen, Verarbeiten, Erklären und Darstellen bekannter Sachverhalte unter vorgegebenen Gesichtspunkten in
einem durch Übung bekannten Zusammenhang und das selbstständige Übertragen und Anwenden des Gelernten auf vergleichbare neue
Zusammenhänge und Sachverhalte
auswerten
beschreiben
Kl. 6 Curriculum Mathematik
Daten, Einzelergebnisse oder sonstige Sachverhalte zu einer abschließenden, begründeten
Gesamtaussage zusammenführen
einen Sachverhalt oder ein Verfahren in vollständigen Sätzen unter Verwendung der Fachsprache
Seite 8 von 4
Schulcurriculum Mathematik
Stand: 03.06.2016
mit eigenen Worten wiedergeben (hier sind auch Einschränkungen möglich: „Beschreiben Sie in
Stichworten“)
bestimmen, ermitteln
Lösungen, Lösungswege beziehungsweise Zusammenhänge finden und die Ergebnisse darstellen, zum Beispiel durch
Skizzen, Rechnung
entscheiden
bei Alternativen sich begründet und eindeutig auf eine Möglichkeit festlegen
erklären, erläutern
Sachverhalte auf der Grundlage von Vorkenntnissen so darlegen und veranschaulichen, dass sie verständlich werden
interpretieren, deuten
Sachverhalte, Phänomene, Strukturen oder Ergebnisse in eine andere mathematische Sichtweise umdeuten oder
rückübersetzen auf das ursprüngliche Problem
skizzieren
die wesentlichen Eigenschaften eines Objekts grafisch vereinfacht darstellen
untersuchen
Sachverhalte, Probleme, Fragestellungen nach bestimmten, fachlich üblichen beziehungsweise sinnvollen Kriterien
bearbeiten
Anforderungsbereich III
Umfasst das Verarbeiten komplexer Sachverhalte mit dem Ziel, zu selbstständigen Lösungen, Gestaltungen oder Deutungen, Folgerungen,
Verallgemeinerungen, Begründungen und Wertungen zu gelangen. Dabei wählen die Schülerinnen und Schüler selbstständig geeignete Arbeitstechniken und
Verfahren zur Bewältigung der Aufgabe, wenden sie auf eine neue Problemstellung an und reflektieren das eigene Vorgehen
begründen, nachweisen, zeigen
beurteilen, bewerten
beweisen
Kl. 6 Curriculum Mathematik
eine Aussage, einen Sachverhalt durch Berechnungen, nach gültigen Schlussregeln, durch Herleitungen oder inhaltliche
Argumentation verifizieren oder falsifizieren
zu Sachverhalten ein selbstständiges Urteil unter Verwendung von Fachwissen und Fachmethoden formulieren und
begründen
Aussagen unter Verwendung von bekannten mathematischen Sätzen, logischen Schlüssen und
Äquivalenzumformungen und unter Beachtung formaler Kriterien verifizieren
Seite 9 von 4