Definitions - ILIAS der Hochschule Harz

Dr. Xenia V. Jeremias
Definitions- und Formelübersicht Mathematik
TH Wildau [FH]
Definitions- und Formelübersicht Mathematik
Mengen und Intervalle
Eine Menge ist eine Zusammenfassung von wohlunterschiedenen Elementen zu einem Ganzen.
Dabei muss entscheidbar sein, ob ein Element zu der Menge gehört oder nicht.
Zahlenbereiche sind spezielle Mengen:
Natürliche Zahlen
Ganze Zahlen
{
Rationale Zahlen
Reelle Zahlen
:
}
Menge aller endlichen und unendlichen Dezimalbrüche
Ein Intervall ist die Menge aller reellen Zahlen, die zwischen zwei gegebenen Zahlen und liegen,
wobei
ist.
Das Zeichen bedeutet „ist Element von“ und wird sowohl bei Mengen als auch bei Intervallen
benutzt. bedeutet im Umkehrschluss „ist nicht Element von“.
Grundrechenarten
Strichrechnung
Summand + Summand = Summe
Minuend – Subtrahend = Differenz
Die Gegenzahl zu einer Zahl bzw. das Negative einer Zahl ist
Es gilt:
sowie
bzw.
Der Betrag einer Zahl, in einer Formel
{
, ist ihr absoluter Wert:
Punktrechnung
Faktor ⋅ Faktor = Produkt
Dividend : Divisor = Quotient
bzw.
Wichtig: Durch darf man nicht teilen!
Der Kehrwert zu einer Zahl
Es gilt:
⋅
sowie
ist
⋅
bzw.
Rechengesetze
Für alle
gelten:
das Kommutativgesetz:
bzw.
⋅
das Assoziativgesetz:
⋅
bzw.
⋅
⋅
⋅
⋅
1
⋅ ⋅
Dr. Xenia V. Jeremias
Definitions- und Formelübersicht Mathematik
⋅
das Distributivgesetz:
TH Wildau [FH]
⋅
⋅
⋅
⋅
bzw.
⋅
⋅
⋅
⋅
⋅
⋅
(„ausklammern“)
Wichtig: Punktrechnung geht vor Strichrechnung! Nur Klammern können diese Reihenfolge ändern!
Bruchrechnung
mit
Erweitern mit
⋅
⋅
Kürzen mit
Addition und Subtraktion gleichnamiger Brüche mit
bzw.
Multiplikation und Division mit
⋅
⋅
⋅
bzw.
⋅
⋅
⋅
Prozentrechnung
: Prozentsatz (%)
: Prozentwert
: Grundwert
Allgemeines zu Gleichungen und Funktionen
Eine Konstante ist ein Platzhalter für einen festen Zahlenwert.
Eine Variable ist ein Platzhalter für einen veränderlichen Zahlenwert.
Ein Term ist eine mathematisch sinnvolle Kombination aus Zahlen, Konstanten, Variablen, Klammern
und Rechenoperationen.
Eine Gleichung ist ein mathematisches Gebilde der Form „ein Term = ein (anderer) Term“.
In einem Produkt aus Zahl und Variable wird die Zahl als Koeffizient bezeichnet.
Die Menge aller Zahlen, die als Lösung einer Gleichung grundsätzlich infrage kommen, wird
Definitionsbereich genannt (Formelzeichen: ).
Eine Zahl heißt Lösung einer Gleichung, wenn sie Element des Definitionsbereichs ist und beim
Einsetzen dieser Zahl in die Gleichung beide Seiten gleich groß werden.
Die Menge aller Lösungen wird Lösungsmenge genannt (Formelzeichen: ).
Eine Funktion ist eine Zuordnung, die jedem Element einer Menge, Definitionsbereich
(Formelzeichen: ) genannt, genau ein Element einer anderen Menge, Wertebereich
(Formelzeichen: ) genannt, zuordnet.
Lineare Gleichungen und Funktionen
Lineare Gleichungen sind Gleichungen, in denen nur spezielle Terme erlaubt sind und zwar: Produkte
aus Konstanten, Zahlen und einer Variable sowie Summen aus diesen Produkten und Zahlen.
Lineare Funktionen lassen sich mithilfe der allgemeinen Geradengleichung beschreiben:
⋅
mit der Steigung
und dem y-Achsenabschnitt
Der Graphen einer linearen Funktion ist eine Gerade.
2
Dr. Xenia V. Jeremias
Definitions- und Formelübersicht Mathematik
TH Wildau [FH]
Potenzen, Wurzeln, Logarithmen
Potenzen
Eine Potenz ist eine abkürzende Schreibweise:
⏟⋅ ⋅
⋅
mit der Basis
Exponenten
Wichtig: Potenzrechnung geht vor Punktrechnung geht vor Strichrechnung!
Zu beachten:
für
für
und
z.B. für
Die Potenzgesetze
Für
und
gerade
und
oder für
und
gelten:
⋅
1. Potenzgesetz
2. Potenzgesetz
⋅
3. Potenzgesetz
⋅
( )
4. Potenzgesetz
⋅
5. Potenzgesetz
Binomische Formeln
1. Binomische Formel
2. Binomische Formel
3. Binomische Formel
⋅
3
und dem
Dr. Xenia V. Jeremias
Definitions- und Formelübersicht Mathematik
TH Wildau [FH]
Wurzeln
√
mit dem Radikanden
und dem Wurzelexponenten
Zu beachten:
√
0
√
für alle
und
für alle
Da sich Wurzeln als Potenzen, nämlich √
, schreiben lassen, reichen die Potenzgesetze.
Logarithmen
mit der Basis
und dem Argument
Zu beachten:
für alle
für alle
und
für alle
und
für alle
Die Logarithmengesetze
Für
;
und
und
gelten:
1. Logarithmengesetz
⋅
2. Logarithmengesetz
( )
3. Logarithmengesetz
( )
Namenskonventionen:
,
⋅
,
Quadratische Gleichungen und Funktionen
Quadratische Gleichungen sind Gleichungen von folgender Form
bzw.
mit den Koeffizienten
Lösung z.B. über die p-q-Formel:
und
√( )
Der Graph einer quadratischen Funktion
ist eine Parabel. Ist
von einer Normalparabel. Für
ist die Parabel nach oben geöffnet, für
Bezogen auf die Scheitelpunktform einer quadratischen Funktion
: eine Streckung
: eine Stauchung
: eine Verschiebung nach rechts
: eine Verschiebung nach links
: eine Verschiebung nach oben
: eine Verschiebung nach unten
4
, spricht man
nach unten.
bewirkt:
Dr. Xenia V. Jeremias
Definitions- und Formelübersicht Mathematik
TH Wildau [FH]
„Besondere“ Punkte von Funktionen
Eine Funktion
hat an der Stelle eine Nullstelle, wenn
gilt.
Eine Funktion
hat an der Stelle ein Minimum (Tiefpunkt), wenn
in einer gewissen
Umgebung von der kleinste Funktionswert ist.
Eine Funktion
hat an der Stelle ein Maximum (Hochpunkt), wenn
in einer gewissen
Umgebung von der größte Funktionswert ist.
Eine Funktion
hat an der Stelle ein Extremum, wenn
in ein Minimum oder ein
Maximum hat.
Ungleichungen
Ungleichungen werden im Großen und Ganzen wie Gleichungen gelöst, allerdings muss in einigen
Fällen das Vergleichszeichen „umgedreht“ werden, z.B. bei der Multiplikation mit negativen Zahlen.
Geometrie
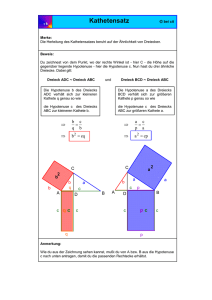
Höhe: die Strecke, die rechtwinkelig auf einer
Dreiecksseite steht und durch die gegenüberliegende Ecke verläuft, hier:
Katheten: die Seiten im rechtwinkligen Dreieck, die
an den rechten Winkel angrenzen, hier: und
Hypotenuse: die Seite im rechtwinkligen Dreieck, die
dem rechten Winkel gegenüberliegt, hier:
Hypotenusenabschnitte: die Abschnitte der
Hypotenuse, die durch den Schnittpunkt von
Höhe und Hypotenuse entstehen, hier: und
Satz des Pythagoras: Die Summe der Flächeninhalte der Quadrate über den Katheten entspricht dem
Flächeninhalt des Quadrats über der Hypotenuse, hier:
Höhensatz: Der Flächeninhalt des Quadrats über der Höhe entspricht dem Flächeninhalt des
Rechtecks, dessen Seiten die Hypotenusenabschnitte sind, hier:
⋅
Kathetensätze: Der Flächeninhalt des Quadrats über einer Kathete entspricht dem Flächeninhalt des
Rechtecks, dessen Seiten die Hypotenuse und der zur Kathete gehörende Hypotenusenabschnitt
sind, hier:
⋅
bzw.
⋅
Umrechnung Gradmaß-Bogenmaß:
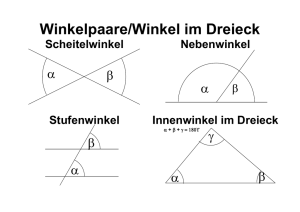
Winkelsummensatz: Die Innenwinkelsumme im Dreieck beträgt
bzw.
Trigonometrie (Bezeichnungen: siehe Dreieck oben)
Sinus:
Kosinus:
bzw.
bzw.
Tangens:
bzw.
Ankathete eines Winkels: Kathete, die an diesen Winkel angrenzt
Gegenkathete eines Winkels: Kathete, die dem Winkel gegenüberliegt
Es gilt für alle :
Trigonometrischer Pythagoras: Es gilt für alle :
5
Dr. Xenia V. Jeremias
Definitions- und Formelübersicht Mathematik
TH Wildau [FH]
Ableitungen
Die Ableitung
(sprich: "f Strich von x") einer Funktion
ist (vorausgesetzt die Ableitung
existiert, was nicht immer der Fall ist) die Funktion, die das Steigungsverhalten von
beschreibt.
Ableitungsregeln
Ausgangsfunktion
Ableitung
⋅
Faktorregel (
⋅
Summenregel
⋅
Produktregel
⋅
⋅
⋅
Quotientenregel (
für alle
)
(
Kettenregel
)
(
⋅
)⋅
Einige Funktionstypen und ihre Ableitungen
Potenzfunktion
mit
und
⋅
Polynomfunktion
mit
⋅
⋅
,
,
und
: Grad des Polynoms
Exponentialfunktion
mit
und
mit
und
mit
und
⋅
√
Wurzelfunktion
√
Logarithmusfunktion
⋅
Sinusfunktion
mit
Kosinusfunktion
mit
Tangensfunktion
mit
Integrale
Gilt
, so ist
eine Stammfunktion der Funktion
nen nennt man unbestimmtes Integral und schreibt dafür:
„Integral f von x dx gleich groß-f von x plus c“).
Bestimmte Integrale von
Stammfunktion
:
. Die Menge aller Stammfunktiomit
(sprich:
(zur Bestimmung orientierter Flächeninhalte) berechnet man über die
[
]
(sprich: „Integral von a bis b über f von x dx
gleich groß-f von x in den Grenzen a und b gleich groß-f von b minus groß-f von a“).
6