Blatt 5 - Goethe

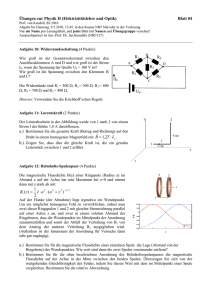
Elektrodynamik - WS 12/13
Organisation Übungen:
Prof. Dr. O. Philipsen
Dr. Wolfgang Unger
Raum 2.105
Goethe-Universität Frankfurt
[email protected]
Übung Nr. 5
vom 16.11.12, Abgabe: 23.11.12 in der Vorlesung
5.1) Helmholtzspule (3+1+2+1 Punkte)
y
~ eines
a) Berechnen Sie die magnetische Induktion B
d ⃗s
Stromrings mir Radius R und Stromstärke I in allen
Punkten, die im Abstand x vom Mittelpunkt entlang der Achse liegen. Gehen Sie dabei folgenderma~ der von einem
R
ßen vor: Zerlegen Sie den Vektor dB,
Leiterelement d~s erzeugt wird, in die Komponente
O
I
dB⊥ und dB|| senkrecht bzw. parallel zur Achse des
~ auf der Achse wird nun
Ringes. Das Gesamtfeld B
von der Summe aller Komponenten dB|| gemacht.
Warum? Berechnen Sie nun dB|| als Funktion von
R, x und ds. Die Integration über alle Leiterelemente ds des Ringes liefert Ihnen einen Ausdruck für die
Feldstärke auf der Achse von der Form
~ ∝ IR2 (R2 + x2 )−3/2
|B|
d⃗
Ba⊥ b
d⃗
B
r
α
⃗a∥b
dB
x
y
(1)
b) Es soll nun das Feld von zwei koaxialen Stromringen für
Punkte auf der Achse berechnet werden: Die Ringe
I
sollen in gleicher Richtung vom Strom I durchflossen
sein, ihr Radius sei R, ihr Abstand 2b. Berechnen Sie
zunächst unter Zuhilfenahme des Ergebnisses von (a)
~ im Punkt P , der sich im Abstand x vom
das Feld B
Mittelpunkt O befindet.
R
R
O
I
x
b
b
~
c) Zeigen Sie, dass für x = 0 die Ableitung d|B|/dx
gleich Null ist. Welche Beziehung muss zwischen
2
~
R und b bestehen, damit auch die zweite Ableitung d2 |B|/dx
an der Stelle x = 0 verschwindet?
Was bedeutet das?
d) Spulen, die der unter (c) gefundenen Bedingung genügen, werden Helmholtzspulen genannt.
~ im Mittelpunkt O für solche Helmholtzspulen.
Berechnen Sie das Feld |B|
5.2) Stromdurchflossener Draht (3+3 Punkte)
a) Bestimmen Sie die magnetische Induktion im Abstand z senkrecht oberhalb eines langen, geraden
Drahtes der Länge L, der einen konstanten Strom I führt. Wie lautet die Antwort, wenn die
Länge des Drahtes unendlich wird?
b) Benutzen Sie ihr Ergebnis aus (a), um die Kraft pro Längeneinheit zwischen zwei unendlich
langen, parallelen Drähten mit Strömen I1 und I2 zu finden, wenn deren Abstand d beträgt.
5.3) Oberflächenstrom (4 Punkte)
~ eines Oberflächenstroms, der die gesamte xy-Ebene
Bestimmen Sie die magnetische Induktion B
bedeckt:
~j(~r) = jδ(z)~ex
(2)
5.4) Vektorpotential (3 Punkte)
Gegeben sei das Vektorpotential eines magnetischen Dipols,
~ × ~r
~ r ) = µ0 m
A(~
.
4π r3
(3)
~ r)
Berechnen Sie die zugehörige magnetische Induktion B(~
André-Marie Ampère (20 January 1775 - 10 June 1836)
French mathematician and physicist who extended Oersted’s results by
showing that the deflection of a compass relative to an electrical current
obeyed the right hand rule. Ampère argued that magnetism could be
explained by electric currents in molecules, and invented the solenoid,
which behaved as a bar magnet. Ampère also showed that parallel wires
with current in the same direction attract, those with current in opposite
directions repel. He dubbed the study of currents electrodynamics, and
also developed a wave theory of heat. Ampère maintained that magnetic
forces were linear, but this proposition was questioned and disproved by
Faraday.
[from: http://scienceworld.wolfram.com/biography/Ampere.html]