Formelsammlung Abschlussprüfung RS
Werbung
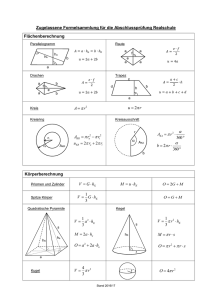
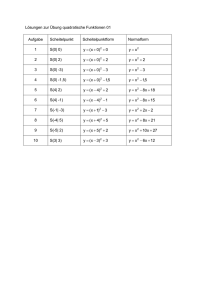
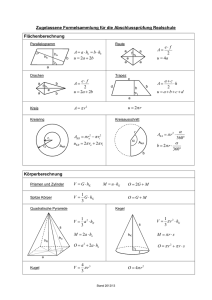
Zugelassene Formelsammlung für die Abschlussprüfung Realschule Flächenberechnung Parallelogramm Raute π΄ = π β βπ = π β βπ ha hb b a a f π΄= e π’ = 2π + 2π a πβπ 2 π’ = 2π a a Drachen a Trapez b f e a c πβπ π΄= 2 π΄= d b h π’ = π+π+π+π π’ = 2π + 2π b π+π ββ 2 a u ο½ 2ο° r A ο½ ο° r2 Kreis Kreisring Kreisausschnitt ri AKR ra r AKR ο½ ο° ra2 ο ο° ri 2 u KR ο½ 2ο° ra ο« 2ο° ri AKA ο½ ο° r 2 ο ο‘ AKA b ο½ 2ο° r ο ο‘ 360 ο° ο‘ 360 ο° b Körperberechnung Prismen und Zylinder V ο½ G ο hK M ο½ u ο hK 1 V ο½ G ο hK 3 Spitze Körper Quadratische Pyramide ha hK . Oο½Gο«M Kegel 1 V ο½ a 2 ο hK 3 s O ο½ 2G ο« M s M ο½ 2a ο ha 1 V ο½ ο° r 2 ο hK 3 M ο½ο°rοs hK O ο½ a 2 ο« 2a ο ha O ο½ ο° r2 ο« ο° r ο s . r a Kugel 4 V ο½ ο° r3 3 r Stand 2016/17 O ο½ 4ο° r 2 Quadratische Gleichungen Normalform: π₯ 2 + ππ₯ + π = 0 π π 2 2 2 π₯1/2 = − ± √( ) − π p-q-Formel: Quadratische Funktionen Scheitelpunktform: π¦ = π(π₯ + π)2 + π ⇒ π(−π|π) Mit π = 1 ist es eine (verschobene) Normalparabel. Trigonometrie Im rechtwinkligen Dreieck gilt: sin(ππππππ) = cos(ππππππ) = tan(ππππππ) = Ξ πΊπππππππ‘βππ‘π π»π¦πππ‘πππ’π π Ankathete Gegenkathete π΄ππππ‘βππ‘π π»π¦πππ‘πππ’π π betreffender Winkel πΊπππππππ‘βππ‘π π΄ππππ‘βππ‘π Hypotenuse Exponentielle Zusammenhänge Wachstum und Zerfall p οΆ ο¦ Gn ο½ G0 ο ο§1 ο± ο· ο¨ 100 οΈ Gn ο½ G0 ο q n Zinseszins n p οΆ ο¦ K n ο½ K 0 ο ο§1 ο« ο· ο¨ 100 οΈ Kn ο½ K0 ο q n n Wahrscheinlichkeitsrechnung Laplace – Wahrscheinlichkeit: Sind alle Ereignisse eines Zufallsexperimentes gleich wahrscheinlich, gilt: P( E ) ο½ Anzahl der günstigen Ereignisse Anzahl aller möglichen Ereignisse 1. Pfadregel (Produktregel): Die Wahrscheinlichkeit eines Ereignisses ist gleich dem Produkt der Wahrscheinlichkeiten entlang des jeweiligen Pfades im Baumdiagramm. 2. Pfadregel (Summenregel): Die Wahrscheinlichkeit eines Ereignisses ist gleich der Summe der Wahrscheinlichkeiten aller der Pfade, bei denen das Ereignis eintritt. Zusammenhang zwischen Dichte, Masse und Volumen π= π π ππ π ππ3 Umrechnungen 1 m³ = 1 000 dm³ 1 dm³ = 1 β = 1 000 cm³ 1 cm³ = 1 000 mm³ Stand 2016/17
