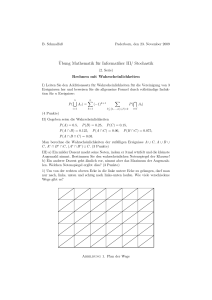
Zufall und Wahrscheinlichkeiten - Fakultät Statistik (TU Dortmund)

Professor Dr. Walter Krämer
Datenanalyse für Journalisten
1. Überblick: Fehler, Pannen und Manipulationen im Umgang mit Statistik.
2. Mittelwerte: Vor- und Nachteile von arithmetischem Mittel und Median. Wie berechnet man
Durchschnitte von Wachstumsraten?
3. Streuungsmaße: Aufbau und Eigenschaften der Standardabweichung.
4. Korrelation: Mechanik und Interpretation des Bravais-Pearson Korrelationskoeffizienten.
Korrelation versus Kausalität.
5. Preisindex für Lebenshaltung: Die Indexformel nach Laspeyres. Zusammensetzung des
Warenkorbs; Problematik der konkreten Preisermittlung.
6. Spezialprobleme von Aktienindices: Mechanik und Wirkungsweise von Dow-Jones und DAX.
7. Grundbegriffe der Wahrscheinlichkeitsrechnung: einfache und
bedingte Wahrscheinlichkeiten; Zufallsvariablen und ihre
Erwartungswerte; die Normalverteilung; das Gesetz der großen Zahl.
8. Grundbegriffe der Mathematischen Statistik: Was ist eine Zufallsstichprobe? Statistische Tests
und der Begriff der „Signifikanz“.
9. Tipps und Tricks für optimale Präsentation von Daten: Grafiken versus Tabellen; optimale
Gestaltung von Tabellen; welche Grafiken für welchen Zweck?
7. Kapitel: Zufall und Wahrscheinlichkeit
Denkste, Kap. 1, 4 und 7; WISO-Skript, Kap. 8, 9 und 10
7. 1 Überblick
7. 2 Zufällige Ereignisse und ihre Wahrscheinlichkeiten
7. 2 Zufallsvariable und Erwartungswerte
7.3 Bedingte Wahrscheinlichkeiten.
Die Welt
Mathematik
Gott existiert – wahrscheinlich
Die Wahrscheinlichkeit, daß Gott existiert, liegt bei 62 Prozent.
Eine 200 Jahre alte Rechenformel hilft bei der Errechnung –
meint das „P.M. Magazin“.
Um zu ihrer Aussage zu kommen, haben die Autoren des Artikels
im aktuellen „P.M. Magazin“ die Mathematik bemüht.
Wahrscheinlichkeits- und Plausibilitätsrechnung wurden mal
nicht für trockene Zahlen angewandt, sondern für die großen
Fragen der Menschheit.
Das P.M. Magazin stellt die Hypothese „Gott existiert“ aus und
wägt ab: Wie wahrscheinlich ist es, daß Gott das Universum
erschaffen hat?
7. Zufall und Wahrscheinlichkeit
7. 2 Zufällige Ereignisse und ihre
Wahrscheinlichkeiten
„Zusammengesetzte“ Ereignisse
Trick zum Ausrechnen von |A|, |Ω|
bei komplizierten Laplace-Experimenten:
k- elementige Teilmengen einer Menge
vom Umfang n.
Anwendung: Lotto
Beispiel für disjunkte (unvereinbare)
Ereignisse beim zweimaligen Würfeln:
Aufgabe:
Jeder vierte Bundesbürger stirbt an Krebs.
Sie lesen in der Zeitung von drei
unzusammenhängenden Todesfällen.
Mit welcher Wahrscheinlichkeit
a) starben alle drei an Krebs?
b) starb genau einer an Krebs?
c) starb mindestens einer an Krebs?