Gabriele Hildmann Volkswirtschaftslehre SS 2011

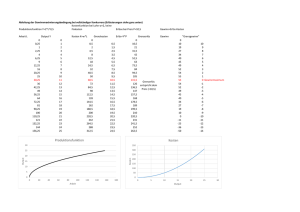
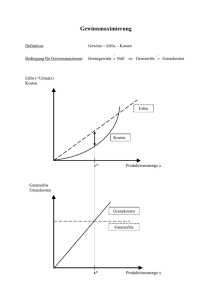
Gabriele Hildmann Volkswirtschaftslehre SS 2011 Lösungsvorschläge zum Aufgabenblatt 2 Achtung! Dies sind Lösungsvorschläge! Andere Formulierungen etc. können genau so rich‐
tig sein. Die Vorschläge sind als Anhaltspunkt zur Überprüfung der eigenen Lösungen gedacht. Bitte kein sklavisches Übernehmen der Vorschläge. 1.
2.
3.
4.
5.
6.
Welchen Zusammenhang stellt die Budgetlinie (=Bilanzgerade) dar? Die Budgetlinie ist der geometrische Ort aller Gütermengenkombinationen, die bei ge‐
gebenen Preisen der Güter und gegebenem Einkommen maximal gekauft werden kön‐
nen. Die Steigung der Budgetlinie entspricht dem Verhältnis der Güterpreise. (Graphik) Wie wirkt sich eine Einkommenserhöhung auf die Budgetlinie aus? Eine Einkommenserhöhung erhöht die Konsummöglichkeiten. Bei unveränderten Prei‐
sen verschiebt sich deshalb die Budgetlinie parallel nach außen und verdeutlich so die gestiegenen Konsummöglichkeiten. (Graphik) Wie wirkt es sich auf die Budgetlinie aus, wenn alle Preise um 10 % steigen? Steigen die Preise in gleichem Umfang, dann können gleichmäßig weniger Güter erwor‐
ben werden. Das Verhältnis der Preise (=Steigung der Budgetlinie) bleibt jedoch unver‐
ändert. Die Budgetlinie verschiebt sich, bei unverändertem Einkommen) parallel nach unten und bringt so den Rückgang an Konsummöglichkeiten zum Ausdruck. (Graphik) Wie wirkt es sich auf die Budgetlinie aus, wenn nur ein Preis steigt und der andere kon‐
stant bleibt. Ändern sich die relativen Preise, dann ändert sich die Steigung der Budgetlinie. Die Bud‐
getlinie dreht sich. Bei gleichen Einkommen ergeben sich neue Konsummöglichkeiten für den Haushalt. (Graphik) Was wird unter einem Haushaltsoptimum verstanden und wie kann es ermittelt werden? Das Haushaltsoptimum ist am Tangentialpunkt der Budgetgeraden mit der Indifferenzkurve erreicht. Es gibt die Gütermengenkombination an, die dem Haushalt unter den gegebenen Bedingungen den höchsten Nutzen erbringt. Welche Kombination des ist, hängt von den Preisen, dem Einkommen und der Nutzenfunktion ab. Es gilt das Maximalprinzip entsprechend lässt sich die Kombination auch mathematisch ermitteln. (Graphik + Erläuterung Budgetlinie und Indifferenzkurve) Welche Identität gilt im Haushaltsoptimum? Im Haushaltsoptimum entspricht die Steigung der Bilanzgrade der Steigung der Indifferenzkurve. Somit entspricht das Verhältnis der Preise dem Verhältnis der Grenz‐
nutzen. Es gilt das 2. Gossensche Gesetz. Es besagt, dass im Haushaltsoptimum der Nut‐
zen, den eine Geldeinheit stiftet in jeder Verwendung gleich ist. (Graphik) 7.
8.
9.
Wie kann die Nachfragefunktion der Haushalte ermittelt werden? Welche Annahmen werden dabei getroffen? Die Nachfragefunktion der Haushalte ergibt sich durch Aggregation der individuellen Nachfragefunktionen. Die Nachfragefunktion eines Haushaltes kann wie folgt ermittelt werden: Ausgehend von der Nutzenfunktion des Haushaltes ergeben sich dessen Indifferenzkurven. Ausgehend von einem gegebenen Preis des anderen Gutes und ei‐
nem gegebenen Einkommen werden dann die Haushaltsoptima ermittelt, die sich bei unterschiedlichen Preisen des untersuchten Gutes ergeben. So ergibt sich, welche Men‐
ge des Gutes der Haushalt bei einem bestimmten Preis des Gutes nachfragen würde. Da sich dieser Zusammenhang jedoch nur indirekt erkennen lässt, wird der Zusammenhang in ein Preis‐Mengen‐Diagramm übertragen, das dann die Nachfrage des Haushaltes ver‐
deutlicht. Beim Umfang mit der Nachfragefunktion sollte nicht vergessen werden, dass sie ermittelten Haushaltsoptima vom Einkommen des Haushaltes, der Nutzenfunktion und dem Preis des anderen Gutes wesentlich beeinflusst werden. Verändert sich eine dieser Variablen, dann verändert sich auch die Nachfragefunktion des untersuchten Gu‐
tes. (Graphik) Erklären Sie wie sich Einkommensänderungen, Preisänderungen des jeweils anderen Gu‐
tes und Veränderungen der Präferenzen auf die Nachfragefunktion auswirken. Alle Erläuterungen gelten unter der Annahme, dass jeweils alle anderen Einflüsse kon‐
stant bleiben. Verdeutlichen lassen sich die Argumente jeweils anhand einer Graphik.  Einkommenserhöhungen führen dazu, dass der Haushalt bei gleichem Preis mehr ei‐
nes Gutes kaufen wird. Die Nachfragekurve verschiebt sich –nicht unbedingt parallel‐ nach außen (und umgekehrt).  Preissenkungen des anderen Gutes verändern die Steigung der Budgetlinie. Die neu‐
en Tangentialpunkte werden dazuführen, dass bei gleichem Preis weniger von dem Gut nachgefragt wird. Schließlich muss sich im neuen Haushaltsoptimum wieder das Preisverhältnis und das Verhältnis der Grenznutzen entsprechen (und umgekehrt).  Veränderungen der Nachfrage führen zu einer neuen Nutzenfunktion und zu neuen Indifferenzkurven. Verschieben sich die Präferenzen zu Gunsten des Gutes, dann wird bei einem gegebenen Preis mehr vom Gut nachgefragt (und umgekehrt). Wie kann die Minimalkostenkombination ermittelt werden und was sagt sie aus? Die Minimalkostenkombination ergibt sich als Tangentialpunkt der Isokostenlinie mit ei‐
ner Isoquante. Die Isokostenlinie stellt alle Inputkombinationen dar, die bei gegebenen Inputpreisen die gleichen Kosten verursachen. Die Isoquante gibt alle Kombinationen der Inputfaktoren an, die zum gleichen Ertrag führen (Graphik). Zudem lässt sie sich na‐
türlich mathematisch bestimmen. Die Minimalkostenkombination gibt an, mit welcher Faktoreinsatzmengenkombination eine bestimmte Produktionsmenge am kostengüns‐
tigsten hergestellt werden kann. 10. Zeigen Sie, wie sich die Kostenfunktion aus der Produktionsfunktion ermitteln lässt. Um die Kostenfunktion zu ermitteln, wird für jede Produktionsmenge zunächst die Mi‐
2
nimalkostenkombination ermittelt. Somit ergeben sich bei gegebenen Preisen die Kos‐
ten für die Herstellung der verschiedenen Produktionsmengen. (Graphik) E
K
x
0
K
K
G
p
E
G
11. Was bringen die Grenzkosten zum Ausdruck und wie können sie ermittelt werden? Die Grenzkosten entsprechen den Kosten für die letzte produzierte Einheit (z.B. die Kos‐
ten der Erzeugung der 25sten Einheit). Kosten die mit der Produktion vorhergehender Produktmengen entstanden sind, bleiben unberücksichtigt. Da die Grenzkostenfunktion der Steigung der Kostenfunktion entspricht, kann sie durch Differenzierung der Kosten‐
funktion ermittelt werden. 12. Was bringen die totalen bzw. die variablen Stückkosten zum Ausdruck und wie lassen sie sich ermitteln? Variable Kosten sind die Kosten, deren Entstehung von der Produktionsmenge abhän‐
gen. Sie werden anhand der Minimalkostenkombination ermittelt. Variable Stückkosten ergeben sich indem diese Kosten auf die Produktionsmenge bezogen werden. Die tota‐
len Stückkosten ergeben sich, wenn zu den variablen Stückkosten die fixen Kosten pro Stück addiert werden. Da in die Fixkosten alle Kosten eingehen, die unabhängig von der Produktionsmenge entstehen, bilden die totalen Stückkosten die Gesamtkosten pro Stück ab, die durch die Herstellung einer bestimmten Produktionsmenge entstehen. 13. Weshalb entsprechen sich im Gewinnmaximum eines Unternehmens, das an einem polypolistischen Markt agiert, Grenzkosten und Grenzerlös? Der Gewinn eines Unternehmens ergibt sich als Differenz zwischen Erlös und Kosten (
     ). Das Gewinnmaximum ist dort erreicht, wo die Steigung der Ge‐
winnfunktion Null ist (und die 2. Ableitung negativ ist). Die Steigung der Gewinnfunktion stellt die Grenzgewinnfunktion dar. Im Gewinnmaximum ist der Grenzgewinn Null. Es gilt:       . Damit ergibt sich, dass im Gewinnmaximum der Grenzerlös den Grenzkosten entspricht. Da sich der Erlös als Preis mal Menge ergibt, entspricht der p
K


p

,  
Ex

E

x
p
E
Grenzerlös dem Preis (
), der wiederum den Grenzkosten ent‐
spricht (   ). Aus Unternehmenssicht sind alle Punkte gewinnmaximal, denen gilt: Grenzerlös gleich Grenzkosten. (Graphik) 14. Warum entsprechen sich in einem polypolistischen Markt Grenzerlös und Grenzkosten? Antwort siehe Frage 4. 15. Wie kann die Angebotsfunktion eines Unternehmens in einem polypolistischen Markt ermittelt werden? In einem polypolistischen Markt erzieht ein Unternehmen seinen maximalen Gewinn, wenn der die Menge produziert, bei der gilt Grenzerlös = Grenzkosten. Da sich der Erlös als Preis mal Menge ergibt, entspricht der Grenzerlös dem Angebotspreis. Entsprechend stellt die Grenzkostenkurve die Angebotskurve des Unternehmens dar. Durch Aggrega‐
tion der einzelnen Angebotsmenge ergibt sich die gesamtwirtschaftliche Angebotsfunk‐
tion. (Graphik) 16. Definieren Sie die Begriffe Gewinnschwelle und Produktionsschwelle. Als Gewinnschwelle wird jener Preis verstanden, bei der Verkaufspreis den totalen Kos‐
3
ten entspricht. Die Produktionsschwelle ist dort, wo der Preis den variablen Kosten ent‐
spricht. Zwar sind in diesem Fall nicht alle Fixkosten gedeckt, durch die Produktion kön‐
nen jedoch zumindest Teile der sowieso entstandenen Fixkosten gedeckt werden. (Gra‐
phik) 4