Addition und Subtraktion von ganzen Zahlen

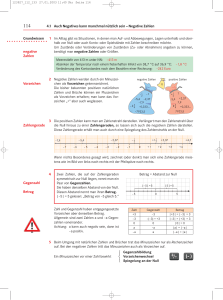
Addition und Subtraktion von ganzen Zahlen Zuletzt hast Du im Matheunterricht das rechnen mit negativen Zahlen kennengelernt. Mit positiven Zahlen, man nennt sie auch natürliche Zahlen, und der Null rechnest Du schon lange. Die positiven Zahlen und die negativen Zahlen zusammen nennt man ganze Zahlen. Ganze Zahlen haben die Besonderheit, dass sie ein Vorzeichen besitzen: ein „+“ für positive Zahlen, zum Beispiel (+4), und ein „–“ für negative Zahlen, zum Beispiel (–3). Ganze Zahlen kann man addieren und subtrahieren. Bei positiven Zahlen kennst Du Dich da schon lange gut aus. Bei den negativen Zahlen muss man nun ganz besonders aufpassen. – Du hast vier verschiedene Vorstellungen im Unterricht kennengelernt, die Dir beim Rechnen helfen können: 



Guthaben/Schulden Figur auf Spielfeld Zahlengerade Plus‐Minus‐Tabelle Alle diese Vorstellungen können Dir helfen, mit ganzen Zahlen zu rechnen, indem Du Dir das entsprechende System vorstellst. Dabei kannst Du die Idee wählen, die Dir selbst am besten hilft. Zum Beispiel die Aufgabe 2 + (‐7) = ? lässt sich verschieden vorstellen: 



Du hast 2€ auf dem Konto und nimmst einen Schuldschein über 7€ auf. Danach hast Du einen Kontostand von ‐5€, also 5€ Schulden. Du stehst auf dem Spielfeld auf Position „+2“. Nun hast Du ein Plus und eine „‐7“ gewürfelt. Also guckst Du in positive Richtung (wegen dem Plus) und gehst dann sieben Schritte rückwärts. Du landest auf dem Feld „‐5“. Die gleiche Überlegung kannst Du auch ohne Spielfeld an der Zahlengerade machen. Wir haben in der Klasse eine Zahlengerade von ‐40 bis +40 an der Tafel. In der Beispielrechnung 2 + (‐7) stehen zwei Rechen‐ bzw. Vorzeichen direkt aneinander: Das „+“ ist das Rechenzeichen, das „–“ ist das Vorzeichen der Zahl ‐7. Wenn zwei Rechenzeichen direkt aneinander stehen (maximal durch eine Klammer getrennt), dann kann man die beiden Zeichnen miteinander „verrechnen“. Aus „+“ und „–“ ergibt sich dann „–
“. Man rechnet also 2 – 7 = ‐5. Wenn Du nun üben willst, dann ist es sinnvoll, nochmal mit den leichteren Aufgaben anzufangen. Eine gute Grundlage, um sich negative Zahlen vorstellen zu können, ist eine Zahlengerade, die Du zum Beispiel vom Thermometer kennst. Du solltest Werte ablesen können. Aufgabe 1: Zeichne in Deinem Heft eine Zahlengerade von ‐10 bis +10. Verwende dabei ein Kästchen für eine Einheit. Aufgabe 2 (mündlich): (zu S. 182 Aufg. 4; Achtung: nicht ins Buch malen!) – Überlege, wo Du bei Aufgabenteil c) eine Markierung für ‐750 machen müsstest. Wo im Aufgabenteil d) für ‐2015 oder für ‐1980? Aufgabe 3*: Lege ein Koordinatensystem an (eine Einheit ein Zentimeter; die beiden Achsen von ‐5 bis +5). Zeichne die drei Punkte A(3/2), B(‐3/‐1) und C(3/‐3) ein. Verbinde zu einem Dreieck und berechne den Flächeninhalt. (Kontrolle: AD=15cm²) Jetzt kannst Du mit Zahlengeraden sicher umgehen. Kannst Du auch Zahlen der Größe nach sortieren? – Tipp: Wenn Du unsicher bist, dann stell Dir die Zahlen auf der Zahlengerade vor. Liegt die Zahl weiter links ist sie kleiner. Liegt die Zahl weiter rechts ist sie größer. Aufgabe 4: Sortiere die folgenden Zahlen der Größe nach. Beginne mit der kleinsten und verwende das „<“‐Zeichen: 43 ‐231 15 ‐17 ‐232 0 ‐5 Zunahmen und Abnahmen sind die „leichteren“ Rechnungen mit ganzen Zahlen. Auch hier hilft Dir vielleicht die Vorstellung von einem Thermometer oder einer Zahlengeraden weiter. (Leichter sind die Aufgaben, weil du positive Zahlen addierst oder subtrahierst. Die Zahl, von der Du „losgehst“, oder das Ergebnis können dabei aber negativ werden.) Aufgabe 5: a) Es ist ‐5°C kalt. Morgen soll die Temperatur um weitere 7°C fallen. b) Du fährst aus der Tiefgarage im 2. Untergeschoss 7 Etagen nach oben. c) In einem Förderkorb im Bergbau fährst Du von 13 Metern über der Erdoberfläche 210 Meter nach unten. Aufgabe 6: Berechne. a)
b)
c)
d)
–20 – 17 13 – 312 –15 + 32 (–32) + 111 Das klappt ja schon ganz gut. Übung bekommst Du über eine Rechentabelle (Achtung: Oben links steht, ob Du plus oder minus rechnest!) Aufgabe 7: + –7 5 13 3 – –9 7 11 4 Aufgabe 8: Übernimm die folgenden Rechnungen in Dein Heft und ersetze das Fragezeichen durch eine passende Zahl: a) ? – 13 = –17 b) –7 + ? = 31 Nun fehlt noch die Addition und Subtraktion von negativen Zahlen. Dabei wird es ja wundersam: 1 + (–3). Das Rechenzeichen plus lässt erstmal vermuten, dass etwas hinzukommt, dass es größer wird. Aber da eine negative Zahl addiert wird, geht es in eine andere Richtung. Stellen wir uns das Kontospiel vor: Bei einem Kontostand von +1€ nimmst Du einen Schuldschein über 3€ auf, rechnest also 1 – 3 = –2.Du landest also insgesamt bei ‐2€. Du kannst auch eine der anderen Vorstellungen verwenden, die ganz am Anfang vom Text erwähnt wurden. Sehr schnell rechnen kannst Du mit der Plus‐Minus‐Tabelle. Plus‐Minus‐Tabelle Rechen‐
zeichen +
–
Vorzeichen
+
–
+
–
–
+
Aus „+“ und „–“ zusammen wird also zum Beispiel „–“. Also: –4 + (–3) = –4 – 3 = –7. Achtung: Nur Plus‐ und Minuszeichen, die direkt miteinander in Verbindung stehen (durch eine Klammer getrennt), werden auf diese Art miteinander „verrechnet“. Das „–“ vor der 4 bleibt im Zwischenschritt stehen. Aufgabe 9: Rechne die Aufgaben mit einem Zwischenschritt. Beispiel: –8 – (–2) = –8 + 2 = –6. a)
b)
c)
d)
e)
–17 + (–13) 17 – (+13) +17 – (–13) –66 – (–44) –113 + (–17) Aufgabe 10: Rechenmauern und Rechenbäume helfen Dir beim Üben (siehe Zusatzblatt). Lösungen: (nicht alle Aufgaben) Aufgabe 1: ‐ Aufgabe 2: ‐ Aufgabe 3*: ‐ Aufgabe 4: ‐232 < ‐231 < ‐17 < ‐5 < 0 < 15 < 43 Aufgabe 5: a) Es ist ‐5°C kalt. Morgen soll die Temperatur um weitere 7°C fallen.  Morgen soll es ‐12°C werden. b) Du fährst aus der Tiefgarage im 2. Untergeschoss 7 Etagen nach oben.  Du landest im 5. Obergeschoss. c) In einem Förderkorb im Bergbau fährst Du von 13 Metern über der Erdoberfläche 210 Meter nach unten.  Nach der Fahrt bist Du 197 Meter unter der Erde. Aufgabe 6: Berechne. a)
b)
c)
d)
–20 – 17 = –37 13 – 312 = –299 –15 + 32 = 17 (–32) + 111 = 79 Aufgabe 7: + –7 5 13 6 18 3 –4 8 – –9 7 11 –20 –4 4 –13 3 Aufgabe 8: Übernimm die folgenden Rechnungen in Dein Heft und ersetze das Fragezeichen durch eine passende Zahl: a) ? – 13 = –17 b) –7 + ? = 31 ? = –4 ? = 38 Aufgabe 9: Rechne die Aufgaben mit einem Zwischenschritt. Beispiel: –8 – (–2) = –8 + 2 = –6. a)
b)
c)
d)
e)
–17 + (–13) = –17 –13 = –30 17 – (+13) = 17 – 13 = 4 +17 – (–13) = +17 + 13 = 30 –66 – (–44) = –66 + 44 = –22 –113 + (–17) = –113 – 17 = –120 Aufgabe 10: ‐