1999 - Frank Haberecht

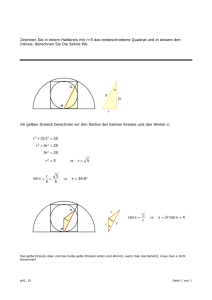
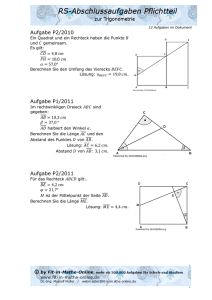
Sächsisches Staatsministerium
für Kultus
Schuljahr 1998/99
Geltungsbereich: für Klassen 10 an
- Mittelschulen
- Förderschulen
- Abendmittelschulen
Schriftliche Abschlussprüfung Mathematik
Realschulabschluss
Allgemeine Arbeitshinweise
Die schriftliche Abschlussprüfung besteht aus zwei Teilen:
Teil I - Plichtaufgaben
Teil II - Wahlaufgaben
Vor der planmäßigen Arbeitszeit stehen Ihnen 15 Minuten zum Vertrautmachen mit
den Aufgaben zur Verfügung.
Die Arbeitszeit zur Lösung aller Aufgaben beträgt 240 Minuten.
Für die Prüfungsarbeit können 40 Bewertungseinheiten erreicht werden. Davon
werden 33 Bewertungseinheiten für den Pflichtteil und 7 Bewertungseinheiten für
den Wahlteil vergeben.
Es ist eine Wahlaufgabe zu bearbeiten. Wird mehr als eine Wahlaufgabe völlig
richtig gelöst, so wird eine Bewertungseinheit zusätzlich erteilt. Eine weitere Bewertungseinheit kann zusätzlich erteilt werden, wenn die Form mathematisch und
äußerlich einwandfrei ist.
Bei mehreren wesentlichen Verstößen gegen die Kriterien einer mathematisch einwandfreien Form wird eine Bewertungseinheit abgezogen. Erfolgen außerdem wesentliche Verstöße gegen die äußere Form, so wird eine weitere Bewertungseinheit
abgezogen.
Geometrische Konstruktionen und Zeichnungen sind auf unliniertem Papier auszuführen. Grafen von Funktionen sind in einem rechtwinkligen Koordinatensystem (Einheit 1 cm) auf Millimeterpapier darzustellen.
Die Lösungsdarstellung muss einen erkennbaren Weg aufzeigen. Das Ergebnis ist
hervorzuheben.
Sie dürfen folgende Hilfsmittel verwenden:
- Tabellen- und Formelsammlung ohne ausführliche Musterbeispiele sowie ohne
Wissensspeicheranhang
- nicht programmierbarer Taschenrechner
- Zeichengeräte und Kurvenschablonen
- Wörterbuch der deutschen Rechtschreibung
Sign 8/1/1
1999
Teil I - Pflichtaufgaben
Aufgabe 1
Gegeben ist eine Funktion f durch die Gleichung y = f(x) =
1
x + 3.
2
a)
Zeichnen Sie den Grafen der Funktion f mindestens im Intervall − 7 ≤ x ≤ 1.
b)
Spiegeln Sie diesen Grafen an der y-Achse.
c)
Das Spiegelbild sei der Graf einer Funktion g.
Geben Sie die Gleichung von g an.
d)
Die beiden Grafen schließen mit der x-Achse ein Dreieck ein.
Bezeichnen Sie die Eckpunkte des Dreiecks und geben Sie deren Koordinaten
an.
e)
Ein anderes Dreieck hat dieselben Eckpunkte auf der x-Achse, als dritten Eckpunkt aber den Punkt P (4; 3).
Begründen Sie, dass beide Dreiecke den gleichen Flächeninhalt haben.
Aufgabe 2
In einem Bebauungsgebiet hat eine Grundstücksfläche folgende Form und Maße:
Berechnen Sie den Preis für das Grundstück, wenn ein Quadratmeter 90,00 DM
kostet.
Sign 8/1/2
1999
Aufgabe 3
Von einem Würfel ABCDEFGH wird das vierseitige Prisma KBCLNFGM abgetrennt
(siehe Skizze).
Es gilt: AB = 6,0 cm,
NF = 1 EF ,
2
KB = 1 AB .
4
a)
Stellen Sie den Restkörper AKLDENMH im Zweitafelbild dar und bezeichnen
Sie die Eckpunkte.
b)
Berechnen Sie das Volumen des Restkörpers AKLDENMH.
c)
Berechnen Sie die Größe des Winkels NKA.
Aufgabe 4
Ein roter und ein blauer Spielwürfel werden nacheinander geworfen. Es interessiert
die jeweils oben liegende Augenzahl.
Bei beiden Spielwürfeln sind die Eintrittschancen für die Augenzahlen 1, 2, ..., 6
jeweils gleich.
a)
Geben Sie ein Ergebnis dieses zweistufigen Zufallsexperimentes an.
Wie viele Ergebnisse gehören insgesamt zur Ergebnismenge S?
b)
Für ein Spiel wird die Augensumme beider Würfel ermittelt.
- Geben Sie alle möglichen Werte für die Augensumme an.
- Berechnen Sie die Wahrscheinlichkeit dafür, dass die Augensumme den
Wert 10 annimmt.
Sign 8/1/3
1999
Aufgabe 5
Eine ebene Figur (siehe Skizze) besteht aus einem gleichschenkligen rechtwinkligen
Dreieck und je einem Halbkreis mit den Durchmessern BC und CA .
a)
Die Länge von BC und von CA sei
jeweils 4,0 cm. Berechnen Sie den
Flächeninhalt der Figur.
b)
Auf wie viel Prozent vergrößert sich
der Flächeninhalt einer solchen Figur,
wenn die Länge von BC und von CA
verdoppelt wird?
c)
Die Länge von BC und von CA sei s.
Zeigen Sie, dass der Flächeninhalt
solcher Figuren mit der Formel
2 
π
A = s2 1 + 

2
berechnet werden kann.
Aufgabe 6
a)
Ein PKW verbraucht für 625 km 45 Liter Kraftstoff.
Berechnen Sie den durchschnittlichen Verbrauch
je 100 km.
b)
Wie viel Prozent der Gesamtfläche
sind grau gekennzeichnet?
c)
Zeichnen Sie den Grafen der Funktion y = f(x) = 3 sin x mindestens im Intervall
− π ≤ x ≤ 2π in ein Koordinatensystem und geben Sie alle Nullstellen im Intervall an.
Sign 8/1/4
1999
d)
e)
Ermitteln Sie die Größe des Winkels α.
Im Waldschadensbericht des Jahres 1997 wird festgestellt, dass von
je 100 Bäumen 41 ohne Schadensmerkmale, 39 schwach geschädigt und
20 deutlich geschädigt sind.
Stellen Sie diesen Sachverhalt in einem Kreisdiagramm dar.
Teil II - Wahlaufgaben
Wahlaufgabe 7.1
Gegeben ist ein Dreieck ABC mit AB = 6,5 cm, BC = 3,8 cm und AC = 9,7 cm.
a)
Konstruieren Sie das Dreieck ABC.
b)
Konstruieren Sie die Mittelsenkrechten der Dreiecksseiten.
Bezeichnen Sie den Schnittpunkt der Mittelsenkrechten mit Z.
c)
Konstruieren Sie das Bilddreieck A1B1C1 vom Dreieck ABC bei der zentrischen
Streckung mit dem Streckungszentrum Z und dem Streckungsfaktor 3 .
2
d)
Berechnen Sie den Umfang des Bilddreiecks A1B1C1.
e)
Ein weiteres Bilddreieck A2B2C2 vom Dreieck ABC hat einen Umfang von
2 400 m.
Ermitteln Sie die Seitenlängen dieses Bilddreiecks.
Sign 8/1/5
1999
Wahlaufgabe 7.2
Zur Ausstattung eines Lesecafés einer Mittelschule werden Kaffeegeschirr und Gläser gekauft. Jeweils 6 Tassen mit Untertassen werden als Set zu 12,00 DM angeboten. Der Preis eines Glases beträgt 0,85 DM.
a)
Die Schüler kaufen 8 Sets und 80 Gläser. Da sie bar bezahlen, erhalten sie 3%
Rabatt.
Berechnen Sie den Kaufpreis.
b)
Die Gläser haben innen die Form eines geraden Kreiszylinders. Der Innendurchmesser beträgt 6,0 cm und die Höhe im Inneren des Glases 9,0 cm.
- Berechnen Sie das maximale Fassungsvermögen eines Glases.
- Berechnen Sie, in welcher Höhe die 0,2-Liter-Markierung angebracht ist.
- Das Glas wird bis zur Markierung gefüllt. Wie viel Prozent des maximalen
Fassungsvermögens sind das?
c)
Nach einem Monat stellen die Schüler fest, dass sowohl Kaffeegeschirr als
auch Gläser nachgekauft werden müssen. Sie erhalten beides zu den oben genannten Preisen - allerdings ohne Rabatt - und bezahlen dafür 27,40 DM.
Wie viele Gläser wurden nachgekauft?
Wahlaufgabe 7.3
Während einer Aktion „Grünes Sachsen“ wurden für die Begrünung von Grundstücken Gelder zur Verfügung gestellt. Es konnten Nadelbäume, Laubbäume und
Sträucher für jeweils gleiche Stückpreise erworben werden.
Eine Familie kaufte für 360,00 DM 2 Nadelbäume und 6 Laubbäume. Für den gleichen Betrag kaufte die Nachbarfamilie 4 Nadelbäume, 3 Laubbäume und einen
Strauch zu 4,50 DM.
a)
Berechnen Sie, wie viel ein Nadelbaum und wie viel ein Laubbaum kostete.
Führen Sie die Probe durch.
b)
Im gesamten Landkreis wurden 98,2% der zur Verfügung gestellten Gelder für
1 322 Nadelbäume, 1 996 Laubbäume und 202 Sträucher ausgegeben. Für
den Restbetrag wurden 486 Pflanzpfähle gekauft.
Berechnen Sie den Preis für einen Pflanzpfahl.
Sign 8/1/6
1999