Aufgabenblatt 21 Impedanzen 1

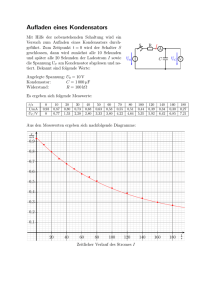
Leistungskurs 12.1
26.01.2009
Aufgabenblatt zu Impedanzen
Aufgabe 128.14 (E 155):
Ein Kondensator mit der Kapazität C = 2 F wird durch Zuleitungen, deren Widerstand vernachlässigt werden
darf, mit einer Wechselspannungsquelle verbunden. Die Effektivspannung beträgt Ueff = 220 V, die Frequenz f =
50 Hz.
a) Welchen kapazitiven Widerstand hat der Kondensator ?
b) Welche effektive und welche Scheitelstromstärke hat der durch den Kondensator fließende Strom ?
c) Wie lauten die Gleichungen für die angelegte Spannung und die Stromstärke ?
Aufgabe 128.15 (E 156)
An einen Kondensator mit der Kapazität C = 4,5 F wird eine Wechselspannung mit der Frequenz f = 50 Hz
angelegt. Die Scheitelstromstärke des durch den Kondensator fließenden Wechselstromes beträgt I 0 = 0,65 A.
Die ohmschen Widerstände der Leitungen sind vernachlässigbar klein. Welche Effektivspannung hat die
angelegte Wechselspannung ?
Aufgabe 128.16 (E 157)
Eine Wechselspannungsquelle wird mit den Anschlüssen eines Kondensators verbunden. Die Effektivspannung
beträgt Ueff = 40 V, die Frequenz f = 50 Hz. In dem Stromkreis fließt ein Wechselstrom mit einer
Effektivstromstärke Ieff = 60 mA. Ohmsche Widerstände treten nicht auf.
a) Welche Kapazität hat der Kondensator ?
b) Wie lauten die Gleichungen für die Spannung U und die Stromstärke I ?
Aufgabe 128.17 (E 159)
Ein Kondensator mit der Kapazität C = 0,1mF und ein Ohmscher Widerstand R sind hintereinander geschaltet
und mit einer Wechselspannungsquelle verbunden. Die Wechselspannung genügt der Gleichung:
U = 2 * 220V * sin (t) ;  = 2  50 s -1
a) Wie muss der Widerstand R gewählt werden, wenn zwischen Strom und Spannung die Phasenverschiebung
f = /4 auftreten soll ?
b) Welche Effektivstromstärke hat der im Kreis fließende Wechselstrom dann ?
c) Wie lauten die Gleichungen für die Spannungen UR bzw. UC, die man an den Kontakten des Ohmschen
Widerstandes bzw. des Kondensators abgreift ?
d) Zeigen Sie, dass die Summe dieser Spannungen gleich der angelegten Wechselspannung ist:
UR(t) + UC(t) = U(T)
An die Ablenkplatten eines Kathodenstrahloszillographen wird eine Schaltung aus zwei Widerständen und zwei
Kondensatoren angeschlossen. Die angelegte Spannung genügt der Gleichung: U = U 0 sin (t);  = 2/50 s-1
Die Kondensatoren haben die Kapazität C = 0,1mF, die Widerstände betragen R = 31,8 k.
Es ist zu begründen, dass die aus zwei gleichartigen Spannungsteilerschaltungen aufgebaute Gesamtschaltung
auf dem Oszillographenschirm einen Kreis zeichnet: Der Leuchtfleck läuft auf der Netzfrequenz f = 50 Hz auf
dem Schirm um.
Anleitung: Es sind die an den x-Platten und an den y-Platten liegenden Wechselspannungen UR bzw. UC zu
ermitteln. Die Ablenkungen x bzw. y des Kathodenstrahles sind diesen Spannungen proportional:
x = k * UR; y = k * UC. x und y genügen einer Kreisgleichung. Verwende dabei die Beziehung
sin (t + /4) = cos (t - /4).