V21 - Operationsverstärker und Feldeffekttransistor

V21 - Operationsverstärker und
Feldeffekttransistor
Christian Wagner
29. Januar 2008
Protokoll von
und
Datum, Uhrzeit:
Betreuer:
Michael Dieblich
Christian Wagner
23.01.2008, 8:30 - 15:30 Uhr
Dr. Marion Friedrich
Inhaltsverzeichnis
1 Einleitung
1
2 Physikalische Grundlagen
2.1 Der Transistor . . . . . . . . . . . . . . . . . . . . . . . . . .
2.1.1 Typen von Transistoren . . . . . . . . . . . . . . . . .
2.1.2 Der Feldeffekttransistor(FET): Aufbau und Funktion .
2.1.3 Kennlinien der FET . . . . . . . . . . . . . . . . . . .
2.2 Operationsverstärker (OPV) . . . . . . . . . . . . . . . . . . .
2.2.1 Gleichtakt- und Differenzsignal . . . . . . . . . . . . .
2.2.2 statische Kennlinie . . . . . . . . . . . . . . . . . . . .
2.2.3 Frequenzgang des OPV . . . . . . . . . . . . . . . . .
2.3 Zu den einzelnen Schaltungen . . . . . . . . . . . . . . . . . .
2.3.1 Summierverstärker und Digital-Analog-Umsetzer . . .
2.3.2 Konstantstromquelle . . . . . . . . . . . . . . . . . . .
2.3.3 Präzisionsgleichrichter . . . . . . . . . . . . . . . . . .
2.3.4 Schwellwertschalter . . . . . . . . . . . . . . . . . . . .
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
1
1
1
1
2
2
4
5
6
6
6
7
7
7
3 Versuchsdurchführung
3.1 Versuchsteil 1 - Summierverstärker . . . . . . . . .
3.2 Versuchsteil 2 - Konstantstromquelle . . . . . . . .
3.3 Versuchsteil 3 - Präzisionsgleichrichter . . . . . . .
3.4 Versuchsteil 4 - Schwellwertschalter . . . . . . . . .
3.5 Versuchsteil 5 - Digital - Analog - Umsetzer (DAU)
3.6 Versuchsteil 6 - Aufnahme der Transistorkennlinie
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
7
9
9
10
10
11
11
.
.
.
.
.
.
11
11
12
13
15
16
18
4 Auswertung und Diskussion
4.1 Versuchsteil 1 - Summierverstärker . . . . . . . . .
4.2 Versuchsteil 2 - Konstantstromquelle . . . . . . . .
4.3 Versuchsteil 3 - Präzisionsgleichrichter . . . . . . .
4.4 Versuchsteil 4 - Schwellwertschalter . . . . . . . . .
4.5 Versuchsteil 5 - Digital - Analog - Umsetzer (DAU)
4.6 Versuchsteil 6 - Aufnahme der Transistorkennlinie
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
5 Zusammenfassung
19
6 Anhang, letzte Angaben, Literaturverzeichnis
19
1 Einleitung
Jeder weiß heutzutage, wie ein Radio funktioniert. Dennoch bleibt ein Problem. Die Ströme,
die aus der Antenne ausgekkoppelt werden, reichen lange nicht aus, um einem Lautsprecher
auch nur einen Mucks zu entlocken.
Aber wie verstärkt man ein Signal so, dass es unverändert bleibt? Die meisten elektronischen Bauelemente haben keine lineare Kennlinie. Wie schafft man es trotzdem, eine lineare
Verstärkung zu erhalten? Und das nicht nur für Gleichstrom, sondern auch für den kompletten
Frequenzgang bei zeitabhängigen Signalen?
Das sind Fragen, die uns dieses Experiment beschäftigen.
2 Physikalische Grundlagen
2.1 Der Transistor
2.1.1 Typen von Transistoren
Der Transistor ist ein Halbleiterbauelement, der aus 2 p-n-Übergängen besteht. Je nachdem,
ob beide Ladungsträgerarten (Elektronen und ”’Löcher”’) am Leitungsvorgang teilnehmen
oder nur eine, unterscheidet man zwischen bipolarem und unipolarem Transistor. Zu den
Bipolaren Transistoren gehören die jedem Schüler bekannten npn- oder pnp-Transistoren.
Der FET - Feldeffekttransistor ist nicht jedem Schüler bekannt und gehört zu den unipolaren
Transistoren.
2.1.2 Der Feldeffekttransistor(FET): Aufbau und Funktion
Es gibt verschiedene Bauweisen der Feldeffekttransistoren, denen alle eines gemeinsam ist:
Das Schaltverhalten wird durch die Manipulation der Bänder im Halbleiter durch ein elektrisches Feld gesteuert. Im Gegensatz zu den bipolaren Transistoren ist also eine leistungslose
Steuerung möglich, während man bei diesen einen Steuerstrom benötigt.
Im Folgenden wird ein SFET, ein selbstleitender Sperrschicht-FET, dargestellt:
Abbildung 1: Aufbau eines SFET
Durch das Anlegen einer Spannung U GS kommt es im N-Kanal zu einer ladungsträgerfreien
Zone. Je nach Größe von U GS werden die Ladungsträger im N-Kanal mehr oder weniger
1
verdrängt und im Extremfall wird die Leitung völlig unterdrückt. Wie diese Kennlinie genau
aussieht, werden wir im Experiment untersuchen.
Legt man keine Spannung an, dann kann Leitung stattfinden, sodass man von einem selbstleitendem SFET spricht. Es gibt auch noch selbstsperrende.
Es gibt auch noch den Metalloxid-Silizium-FET (MOSFET), dessen Aufbau beispielhaft gezeigt werden soll:
Abbildung 2: Der Aufbau eines selbstsperrenden MOSFET
Hier wird durch das Anlegen einer Steuerspannung U GS das Leitungsband so verbogen, dass
Elektronen aus dem p-Substrat in den Bereich des elektrischen Feldes gelangen können und
dadurch eine kleine Zone mit negativen Ladungsträgern überflutet wird. Dieser n-leitende
Bereich wird zum Ladungsträgertransport genutzt.
Der Name des Transistors rührt von seinem Aufbau: das elektrische Feld wird durch eine
Metallplatte erzeugt, die durch eine isolierende SiO2 -Schicht vom Halbleiter getrennt ist. Bei
zunehmender Miniaturisierung erkennt man, dass hier sog. Leckströme aufgrund quantenmechanischer Effekte zwischen Gate (G) und Source (S) fließen können. Um das zu verhindern,
arbeitet man an besseren Isolatoren.
2.1.3 Kennlinien der FET
Die Kennlinie eines Transistors ist durch den typischen Knick gekennzeichnet, sodass eine
nichlineare Verstärkung auftritt. Hier eine Übersicht verschiedener Kennlinien (siehe Abb.3):
Man erkennt aber bestimmte, lineare Bereiche. Diese werden für den sog. Operationsverstärker
ausgenutzt.
2.2 Operationsverstärker (OPV)
Das Ziel ist nun, die Verstärkung linear zu machen. Dazu nutzt man den in etwa linearen
Bereich der Transistoren aus. Weil die Kennlinie der Halbleiter sehr stark von thermischen
Einflüssen abhängt, muss man zuerst diesen Einfluss ausschalten. Das ist der Sinn eines
Differenzverstärkers, der im Folgenden dargestellt wird:
Die Verstärkung der Spannung U E ist U A = vU E . Zusätzlich wird durch den thermischen
Einfluss eine Spannung Uϑ addiert, sodass U A1,2 = Uϑ + v E1,2 . Es folgt: U A1 − U A2 = v(U E1 −
2
Abbildung 3: Die Kennlinien verschiedener Transistoren in der Übersicht
Abbildung 4: Der Aufbau eines Differenzverstärkers
3
U E2 ). Das funktioniert allerdings nur, wenn die beiden Transistoren thermisch eng gekoppelt
sind.
Das ist der erste Schritt in Richtung Operationsverstärker. Als nächstes benötigt man eien
asymetrische Verstärkung und um am Verbraucher den Arbeitspunkt ordentlich einstellen zu
können, einen niederohmigen Ausgang.
Im Endeffekt sieht ein Operationsverstärker folgendermaßen aus:
Abbildung 5: Der Aufbau eines Operationsverstärkers
Über die Anschlüsse U+ und U− wird der OPV mit der nötigen Spannung versorgt. Man kann
an dieser Schaltung zeigen, dass die Ausgangsspannungsdifferenz von der Eingangsspannungsdifferenz abhängt, und zwar mit
∆U A1 =
vD
∆U E
2
mit v D = −
RC β
rBE
Dabei ist β der Stromverstärkungsfaktor zwischen Basis und Emitter und rBE der Widerstand,
der dort herrscht. Damit ist auch die Leerlaufverstärkung ∆U A = 0, wenn U E1 = U E2 = 0
ist.
Die Linearität wird hier durch die in etwa lineare Stromverstärkung (I C = βI B ) des Transistors angenommen. Die Beziehung gilt, wenn I E konstant ist. Ob das gerechtfertigt ist, werden
wir spätestens im Experiment sehen.
2.2.1 Gleichtakt- und Differenzsignal
Die Gleichtaktverstärkung entsteht, wenn man an beiden Eingängen die gleiche Spannung
RC
U Gl anlegt. Damit erhält man ∆U A1 = − 2R
∆U Gl = v Gl ∆U Gl .
E
D
Diese Gleichtaktverstärkung ist natürlich unerwünscht und daher muss G := vvGl
1, d.h.
rBE
RBE β . Dieser Faktor G heißt Gleichtaktunterdrückung. Diese wird dadurch erreicht,
indem man anstelle des Widerstandes RE einen weiteren Transistor schaltet und weitere
Bauelemente dazu, sodass G > 105 wird.
4
2.2.2 statische Kennlinie
Die statische Kennlinie des OPV sieht so aus:
Abbildung 6: Die Kennlinie eines statischen Operationsverstärkers
Man erkennt einen linearen Verstärkungsbereich. Dieser wird, entsprechend der Anwendung,
angepasst. Diese Linearität gilt jedoch nicht im strengen Sinn. Damit man das dämpfen kann,
verwendet man das PRinzip der Gegenkopplung. Die Grundidee ist, die Ausgangsspannung
auf den Eingang so zurückzuführen, dass die Wirkung dieser teilweise kompensiert wird. Der
Schaltungsaufbau sieht folgendermaßen aus:
Abbildung 7: Die Kennlinie eines statischen Operationsverstärkers
v0
1
Es ergibt sich die Klemmverstärkung v kl = 1+kv
mit dem Koppelfaktor k = R1R+R
. Entwi0
2
ckelt man diesen Ausdruck in einer Reihe, erkent man, dass die Klemmverstärkung in erster
2
Linie durch das Verhälnis der Widerstände R
R1 bestimmt wird. Dadurch werden Einflüsse auf
5
die Leerlaufverstärkung wie Temperaturschwankungen etc. gedämpft.
2.2.3 Frequenzgang des OPV
Ein idealer Operationsverstärker verstärkt jede Frequenz linear. In der Realität sieht das
anders aus: Der OPV wirkt gleichzeitig als Tiefpass:
Abbildung 8: Der Frequenzgang eines Operationsverstärkers
Dieses Problem behebt man dadurch, indem man einen Kondensator als Kompensationstiefpass vorschaltet und dadurch zwar eine noch geringere Bandbreite erhält, aber den Phasendrehwinkel in dem Bereich von −90 ◦ . . . 90◦ verschiebt. Das hat den Vorteil, dass die
Verstärkung bei Gegenkopplung stabil bleibt. Würde die Phasendrehung |ϕ| > 90◦ , käme
es bei der Gegenkopplung nicht zu einer Abschwächung, sondern einer Verstärkung des Eingangssignals in einem gewissen Frequenzbereich, der zur Resonanzkatastrophe führen könnte.
2.3 Zu den einzelnen Schaltungen
Die Schaltungen sind den Abbildungen 9 bis 14 im Kapitel ”’Versuchsdurchführung”’ zu
entnehmen.
2.3.1 Summierverstärker und Digital-Analog-Umsetzer
Zur rein theoretischen Betrachtung werden die Widerstände durch eien Widerstand RI ersetzt.
Der Widerstand R besitzt in der Schaltung keine Funktion, die die Verstärkung anbelangt. Die
Klemmverstärkung v kl := UU 0I ergibt sich aus der Schaltung durch v kl = − 10RkΩ
. Der Quotient
I
n
P
UI
Ui
RI lässt sich bei einer Parallelschaltung der Widerstände auch als Summe
Ri darstellen,
i=1
6
wobei n die Anzahl der Widerstände ist und Ui die am Widerstand Ri angelegte Spannung
ist. Damit erhält man für die Ausgansspannung
U0 = −
n
X
Ui
i=1
Ri
· 10 kΩ.
Beim Digital-Analog-Umsetzer sind anstelle der Widerstände die Leitwerte G := R1 eingetragen, sodass sich die binäre Verstärkung ergibt. Bei konstanter Eingangsspannung U I erhält
man
U 0 = −U I ZG · 10 kΩ,
wobei Z eine Zahl von 0 . . . 7 darstellt, die je nach Schaltzustand ermöglicht wird.
2.3.2 Konstantstromquelle
Die am invertierendem Eingang des OPV anliegende Spannung wird durch den Strom I
beeinflusst. Je geringer dieser Strom ist, desto größer ist die Spannungsdifferenz am OPV. Das
verstärkte Signal wird nun an die Basis weitergegeben und führt zum verstärktem Stromfluss.
Es wird sich nach einer kurzen Einstellzeit ein vom Widerstand RL unabhängiger Strom
einstellen.
2.3.3 Präzisionsgleichrichter
Durch das Vorschalten eines OPV vor die Gleichrichtung sollte eine präzisere Spannungsgleichrichtung erfolgen als ohne OPV, zumal dadurch die Möglichkeit besteht, auch Spannungen
unterhalb der Gegenspannung des p-n-Übergangs gleichzurichten. Zur Stabilisierung ist diese Schaltung gegengekoppelt. Diese Gegenkopplung schwächt das negative Spannungssignal
weiter ab, aber lässt das positive weitgehend unverändert hindurch. Der 10 kΩ-Widerstand
dient lediglich zur Einstellung der Verstärkung des OPV, sodass die Spannungsübertragung
1:1 beträgt. (analog Summierverstärker)
2.3.4 Schwellwertschalter
Die Aufgabe eines Schwellwertschalters ist, beim Überschreiten einer gewissen Eingangsspannung eine diskrete Ausgangsspannung zu erzeugen und unterhalb dieser Schwelle keine.
Das wird durch die Rückkopplung des verstärkten, invertierten Eingangssignals auf den positiven Eingang des OPV erreicht. Je nach Betrag der Eingangsspannung wird damit die
Spannungsdifferenz am Eingang des OPV erhöht oder verringert.
3 Versuchsdurchführung
Für die ersten 5 Teilversuche verwendeten wir folgende Geräte:
ˆ Schaltungskasten Typ 741
ˆ Digitalmultimeter Voltcraft M-3610 D
7
ˆ Spannungsquellen HAMEG HM 8040-2 und HM 8030-5
ˆ Speicheroszilloskop HAMEG Combiscope
ˆ Dekadenwiderstände
ˆ SFET B245
8
3.1 Versuchsteil 1 - Summierverstärker
Abbildung 9: Aufbau der Verstärkungsschaltung
Durch Messung der Ausgangsspannung U 0 und Kenntnis der Eingangsspannung U 1,2,3 kann
man die Verstärkung dieser Schaltung bzw. die ohm’schen Widerstände R1,2,3 bestimmen.
Wir bestimmten durch einzelnes Ansprechen der Widerstände die Ausgangsspannung und
ermittelten daraus die zugehörigen Verstärkungsfaktoren sowie den Betrag der Widerstände.
Anschließend schalteten wir alle 3 Widerstände zu und ermittelten die summierte Verstärkung.
3.2 Versuchsteil 2 - Konstantstromquelle
Abbildung 10: Aufbau einer Konstantstromquelle
Dieser Aufbau dient als Konstantstromquelle, d.h. der Ausgangsstrom sollte unabhängig vom
Lastwiderstand RL sein. Dies überprüfen wir im Teilexperiment b), im Teil a) nehmen wir
die Strom-Spannungs-Kennlinie auf.
9
3.3 Versuchsteil 3 - Präzisionsgleichrichter
Abbildung 11: Aufbau des Präzisionsgleichrichters
Hier bestimmen wir die Übertragungskennlinie, d.h. welche Eingangsspannung U I welcher
Ausgangsspannung U 0 entspricht.
3.4 Versuchsteil 4 - Schwellwertschalter
Abbildung 12: Aufbau eines Schwellwertschalters mittels OPV
Wir legten eine Wechselspannung mit f = 100 kHz an den Eingang U I und stellten die
Ausgangsspannungsdifferenz im Dualbetrieb des Oszilloskopen über der Eingangsspannungsdifferenz dar.
Nach Umschalten in den x-y-Betrieb stellten wir ein Hystereseverhalten fest.
10
3.5 Versuchsteil 5 - Digital - Analog - Umsetzer (DAU)
Abbildung 13: Aufbau der Digital-Analog-Schaltung
Durch Kalibrieren der Schaltung stellten wir sie so ein, dass die Spannung für ein Bit genau 1 V
beträgt. Anschließend untersuchten wir verschiedene Schaltkombinationen, um festzustellen,
ob die Summation wirklich funktioniert. (analoge Schaltung zu Versuchsteil 1)
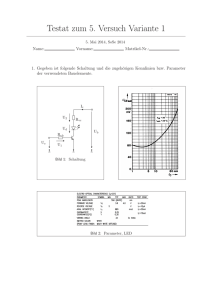
3.6 Versuchsteil 6 - Aufnahme der Transistorkennlinie
Abbildung 14: Schaltung für die Aufnahme der Transistorkennlinie
a) Aufnahme der Steuerkennlinie bei U DS = 15 V b) Aufnahme der Ausgangskennlinie bei
U GS = {0|0, 5|1, 0|1, 5} V
4 Auswertung und Diskussion
Die der Auswertung zugrundeliegenden Messdaten befinden sich im Anhang.
4.1 Versuchsteil 1 - Summierverstärker
0
In der Schaltung gilt folgende Formel für die Verstärkung: U 0 = − 10 R000Ω
U I = v0U I.
I
Damit sollte sich im 2. Versuchsteil eine resultierende Gesamtspannung von U 0 = −5, 02 V
ergeben. Gemessen wurde U 0 = −4, 9 V .
11
U I1 /V
2
3
RI /Ω
U 0 /V
-2,08
-3.06
v0
1,04
1,02
1,03
9708
U I2 /V
1
0.51
U 0 /V
-2.08
-1,06
v0
2.08
2,08
2,08
4807
U I3 /V
0.2
0.3
U 0 /V
-0.86
-1.26
v0
4,3
4,2
4,25
2353
Tabelle 1: Die Messwerte am Summierverstärker mit zugehörigen Widerständen und
Verstärkungsfaktoren
Da wir diesen Versuchsteil nicht anschließend, sondern zum Schluss nachgeholt haben, könnte es sein, dass sich der Operationsverstärker erwärmt hat. Es wurde keine gegengekoppelte
Schaltung verwendet, sodass dieser Einfluss gegeben sein könnte. Abhilfe schafft eine Temperaturmessung, die jedoch nicht durchgeführt wurde. Es könnte aber auch an der Nichtlinearität
der Kennlinie des OPV liegen.
Durch die Aufnahme mehrerer Schaltzustände in dieser Betriebsart zu diesem Zeitpunkt erhielten wir bei der Zuschaltung von R1 und R2 eine Ausgangsspannung von 4,16 V ergeben
und bei Verwendung von R3 0,84 V. Das macht in Summe 5 V. Damit ist klar, dass es nicht
an der Temperatur liegt, sondern eher an der Nichtlinearität des Verstärkers.
4.2 Versuchsteil 2 - Konstantstromquelle
Für die Strom-Spannungs-Kennlinie der Konstantstromquelle ergibt sich folgendes Bild (Die
Fehler des Messgerätes wurden mit 2% beim Digitalmultimeter veranschlagt und eine absolute
Abweichung von 0,02 V bei Spannungsmessungen beim Oszilloskop):
Abbildung 15: Die Kennlinie der Konstantstromquelle
Die Aufnahme des Emitterstromes über dem Ausgangswiderstand RL ergab folgende Mess-
12
kurve:
Abbildung 16: Die Kennlinie der Konstantstromquelle
Der Abfall bei den Widerständen, die größer als 2 kΩ sind, lässt sich einfach dadurch erklären,
dass die Leistungsgrenze der Schaltung erschöpft ist. Aus dem Ohm’schen Gesetz (gilt für
diese Schaltung, siehe Abb. 15) und der Vorschrift, dass P = U I erhält man P = RI 2 ,
sodass I ∼ R−1/2 ist. Dieser Verlauf ist in etwa zu erahnen. (Anhand der Grafik könnte
man jeden beliebigen Verlauf R−a (a > 0) oder e−aR annehmen, aber die Deutung durch die
Grenzleistung ist naheliegend.)
Dazu ist zu bemerken, dass die Messung mit Widerständen RL > 2 kΩ optional war. Innerhalb
des geforderten Bereiches war der Strom für jeden Verbraucher tatsächlich konstant.
4.3 Versuchsteil 3 - Präzisionsgleichrichter
Die Übertragungskennlinie sieht wie folgt aus (Abb. 17):
Dieser Spannungsknick am Nulldurchgang entsteht wahrscheinlich durch die Gegenkopplung
des abzuschneidenden Spannungssignals, sodass ein Teil invertiert verstärkt wird. Schöner
wäre es, wenn diese Spannungen komplett abgeschnitten würden, wie im theoretischen Verlauf
dargestellt.
Im 2. Versuchsteil dieses Teilversuches legten wir eine Wechselspannung mit f = 100 Hz und
U 1 = 2 V bzw. U 1 = 0, 285 V an und stellten die Ausgangsspannung auf dem Oszilloskop dar
(Abb.18):
Bei den Messungen wurde wahrscheinlich die Masse des Oszilloskopen auf + geschalten, wodurch die Gleichrichtung bei 2 V Effektivspannung nicht richtig funktionierte. Wie man sieht,
funktioniert es bei 0,285 V besser. Dort ist, im Gegensatz zur Übertragungskennlinie, ein sauberes Abschneiden der Kurve sichtbar. Der Unterschied kommt wahrscheinlich aufgrund des
13
Abbildung 17: Die Übertragungskennlinie des Präzisionsgleichrichters
zeitabhängigen Signals zustande. Die Verstärkung durch Gegenkopplung kam dadurch nicht
so sehr zum Tragen.
14
(a) U eff = 2V
(b) U eff = 0, 285V
Abbildung 18: Die Messung der gleichgerichteten Ausgangsspannung
4.4 Versuchsteil 4 - Schwellwertschalter
Hier wurde ein Schwellwertschalter konstruiert, den wir mit einer Wechselspannung (f =
1 kHz, U I,eff = (7, 05 ± 0, 01)V ) belasteten und folgendes Bild im Dualbetrieb auf dem Oszilloskop feststellten:
Aus dieser Darstellung kann man die Schwellspannung leicht ablesen: U S ≈ (5, 2 ± 0, 5) V.
Der Fehler ist in etwa der Ablesefehler, geschätzt.
15
Abbildung 19: Das Signal eines Schwellwertschalters, Eingangssignal: Sinuskurve, Ausgangssignal: Rechteckkurve
Es ist leicht nachzuvollziehen, dass sich ein Hystereseverhalten in der x − y−Darstellung
beobachten lässt (Abb. 20):
In Abbildung 20 c) erkennt man nur einen Strich und sieht deutlich, dass die notwendige Schwellspannung nicht erreicht wurde. Wir haben die Spannung eingestellt, bei der der
Schwellwert noch nicht erreicht wurde und stellten eine Spannung von U S = 5, 05 V fest.
Diese wurde aus der vom Oszilloskop exportierten Wertetabelle entnommen. Das steht im
Einklang mit dem oben abgelesenen Wert.
Die Darstellung stellt gleichzeitig die Übertragungskennlinie dar. Oberhalb des Schwellwertes
wird die Ausgangsspannung U A angezeigt und es findet der Sprung statt. Unterhalb des negativen Schwellwertes springt die Ausgangsspannung auf das die negative Ausgangsspannung
zurück. Aufgrund dieser Tatsache ist das Hystereseverhalten erkennbar. Der Schalter springt
nicht sofort mit dem Absinken unter den Schwellwert zurück.
Das Ausgangssignal ist, abgesehen von den Flanken endlichen Anstiegs und dem Rauschen,
rechteckig, also genau das, was theoretisch zu erwarten war.
4.5 Versuchsteil 5 - Digital - Analog - Umsetzer (DAU)
Diese Schaltung ist analog der Schaltung in Versuchsteil 1. Dabei sind anstelle der Wi0
derstände die Leitwerte G eingezeichnet. Mit der Formel in Versuchsteil 1 U 0 = − 10 R000Ω
UI =
I
v 0 U I , modifiziert zu U 0 = −100 000ΩnGU I , wobei n ∈ N ≤ 7 ist. Durch die gewünschte 1:1Wandlung ergibt sich G = 1001000 Sv.
Die Ausgangsspannung ergibt sich in erster Näherung durch U [V ] =
2
P
ci 2i , wobei ci je nach
i=0
Schaltzustand des i-ten Bits 0 oder 1 ist. Abweichungen entstehen, wie in Teilexperiment 1,
durch die Nichtlinearität der Kennlinie.
16
(a) mit ”Überschwinger”
(b) ohne ”Überschwinger”
(c) unterhalb der Schwellspannung
Abbildung 20: verschiedene Effekte bei der x − y−Darstellung
17
4.6 Versuchsteil 6 - Aufnahme der Transistorkennlinie
Die Kennnlinien des Transistors sehen folgendermaßen aus:
Abbildung 21: Die Steuerkennlinie des Transistors
Abbildung 22: Die Ausgangskennliniedes Transistors
Anhand der Kennlinien und der Übersicht (Abb. 3) ist ersichtlich, dass es sich um einen
n-Kanal-SFET handelt. Das ist in Übereinstimmung mit dem Schaltzeichen in Abb.14.
18
5 Zusammenfassung
Es wird in diesem Versuch deutlich, dass ein Operationsverstärker äußerst vielseitig und
zweckmäßig eingesetzt werden kann. Gerade deshalb ist er von so großer Bedeutung in der
Elektrotechnik und in der Messtechnik (als Messverstärker), um nur zwei Beispiele zu nennen.
Gerade am letzten Versuchsteil wird deutlich, dass eine lineare Verstärkung keineswegs trivial
ist und das Prinzip der Gegenkopplung nur oberflächlich angerissen wurde.
Unter Umständen ließe sich ein Versuchsteil mit der Aufnahme einer Frequenzkennlinie realisieren, ohne den zeitlichen Rahmen übermäßig zu belasten. Jedoch sind wir - auswertungsbedingt - mit diesem Arbeitsaufwand ausreichend beschäftigt.
6 Anhang, letzte Angaben, Literaturverzeichnis
Unterschrift: . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .29. Januar 2008
(Christian Wagner)
Unterschrift: . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .29. Januar 2008
(Michael Dieblich)
Literatur
[1]
http://img116.imageshack.us/img116/7194/. . .
uebersichteingangskennlinieausgangskennlinieunipolartlu2.png
19