3. Schulaufgabe aus der Mathematik Lösungshinweise Gruppe A

3. Schulaufgabe
Klasse 7b
(v0.02 08.05.10)
MSG Würzburg
Schuljahr 2009/2010
3. Schulaufgabe aus der Mathematik Lösungshinweise
Gruppe A
Aufgabe 1
2 + 4 + 7 + 9 + 3 + 0 = 25. Zählt man
alle Noten zusammen, dann bekommt man: 2 · 1 + 4 · 2 + 7 · 3 + 9 · 4 + 3 · 5 + 0 · 6 =
2 + 8 + 21 + 36 + 15 = 82.
Somit beträgt der Notendurchschnitt: D = 82 : 25 = 3, 28
Die Gesamtzahl der Schüler ist
(Hinweis: Zum Berechnen der Division durch 25 im Kopf: Multipliziere die Zahl
zunächst mit 4 und teile dann durch 100. Durch 100 Teilchen bedeutet einfach, das
Komma um zwei Stellen nach rechts verschieben.)
(3 Punkte)
Aufgabe 2
(a) Zur Vereinfachung von
7a · 2x2 q − 7x · a2 · q − 3, 5x · qx · a
werden natürlich zuerst die Produkte vereinfacht (also Zahlen multiplizieren
und Zahl der Multiplikationen der gleichen Variablen gibt die Hochzahl; dann
noch Variablen alphabetisch ordnen), das ergibt:
7a · 2x2 q − 7x · a2 · q − 3, 5x · qx · a = 14aqx2 − 7a2 qx − 3, 5aqx2 .
Anschlieÿend können noch die gleichartigen Terme also die Terme, die bis
auf die Zahlenfaktoren übereinstimmen zusammengefasst werden, das gibt
(Gleichartige Terme werden zusammengefasst, indem man die Zahlenfaktoren
zusammenzählt und die Variablen beibehält):
14aqx2 − 7a2 qx − 3, 5aqx2 = 10, 5aqx2 − 7a2 qx.
(3 Punkte)
(b) Bei dieser Aufgabe muss man zunächst die Klammer ausmultiplizieren (alles
mit allem ) wobei die Rechenregeln für Vorzeichen zu beachten sind. Anschlieÿend
kann man wie oben die Produkte vereinfachen und dann gleichartige Terme
zusammenfassen.
− 2q(q − p) + (q 2 + 3) · (5 − q 2 ) + 4(q − 3)
= −2qq 2 + 2pq + 5q 2 − q 4 + 15 − 3q 2 + 4q − 12
= 2pq − q 4 + 3 + 4q.
(6 Punkte)
3. Schulaufgabe
(v0.02 08.05.10)
Aufgabe 3
MSG Würzburg
Klasse 7b
Schuljahr 2009/2010
Um die Ausgangsgleichung
3(y + 7) − y + 2 = 5y + 8 − (y + 3)
zu lösen, multipliziert man zunächst auf beiden Seiten die Klammern aus, und fasst
zusammen:
3y + 21 − y + 2 = 5y + 8 − y − 3
2y + 23 = 4y + 5
Jetzt formt man die Gleichung so um, dass alle Terme mit
y
auf einer Seite stehen
(zum Beispiel auf der linken Seite), dies erreicht man dadurch, dass man auf beiden
Seiten
− 4y
rechnet:
−2y + 23 = 5.
Nun rechnet man auf beiden Seiten der Gleichung
alle Terme ohne
y
−23,
um dafür zu sorgen, dass
auf der rechten Seite sind:
−2y = −18.
Zum Schluss muss man die gesamte Gleichung nur noch durch
−2
dividieren und
erhält:
y = 9.
y = 9 auf der linken Seite einsetzt,
erhält man: 3 · (9 + 7) − 9 + 2 = 3 · 16 − 7 = 48 − 7 = 41;
und für die rechte Seite 5 · 9 + 8 − 9 + 3 = 45 + 8 − 12 = 41,
Dann noch die Probe durchführen.
Wenn man
also stimmen linke und rechte Seite überein.
Hinweis: Die schriftliche Durchführung der Probe war für die Schulaufgabe nicht
verlangt.
Die Lösungsmenge ist somit
L = {9}.
(6 Punkte)
Aufgabe 4
Um zu ermitteln, wie viele Karten jeweils in einer Kategorie verkauft
wurden, setzt man als Unbekannte die Anzahl der verkauften Karten in einer
bestimmten Kategorie, zum Beispiel der Kategorie 1
(man kann als Variable auch
die Zahl der verkauften Karten in Kategorie 2 nehmen, dann ist die Rechnung
sogar etwas einfacher. Dies sei als Übung empfohlen. Nimmt man als Unbekannte
die Zahl der Karten in Kategorie 3, dann wird die Rechnung ziemlich kompliziert,
das ist nicht zu empfehlen.)
Wenn man mit
a
die Zahl der Karten in Kategorie 1 bezeichnet, dann ist
1
2a
die Zahl der Karten für Kategorie 2, weil hiervon halb so viele wie in Kategorie
3. Schulaufgabe
MSG Würzburg
Klasse 7b
(v0.02 08.05.10)
Schuljahr 2009/2010
1 verkauft wurden. Die Anzahl der Karten für Kategorie 3 ist halb soviel, wie in
1
·
2
|{z}
Kategorie 4 und 1 zusammen, also
1
( a + 180)
|2 {z }
. Also gilt:
halb so viel wie in Kategorie 1 und 4 zusammen
•
Anzahl Karten Kategorie 1:
a
•
Anzahl Karten Kategorie 2:
1
2a
•
Anzahl Karten Kategorie 3:
1
2
•
Anzahl Karten Kategorie 4:
180
· (a + 180)
Weil die Zahl der insgesamt verkauften Karten 1510 ist, erhält man die Gleichung:
1
1
a + a + · (a + 180) + 180 = 1510.
2
2
Diese kann man noch nach bekanntem Schema lösen (vergleiche Aufgabe 3):
1
1
a + a + a + 90 + 180 = 1510.
2
2
2a + 270 = 1510
2a = 1240
a = 620.
Die Zahl der Karten in Kategorie 2 ist dann
1
Kategorie 3 beträgt ·(620+180)
2
1
2 ·620
= 310, Die Zahl der Karten in
= 400 und in Kategorie 4 wurden wie angegeben
180 Karten verkauft.
Die Probe ergibt:
620 + 310 + 400 + 180 = 1510.
(7 Punkte)
Aufgabe 5
Die 5 Titel von Brasilien entsprechen
27 79 %,
also sind
27 97 ,
•
Prozentsatz:
•
Prozentwert: 5
gegeben, und der Grundwert (die Zahl aller vergebenen Titel) ist gesucht. Die
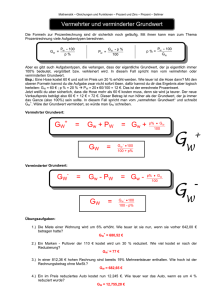
gegebenen Werte eingesetzt in die Grundgleichung der Prozentrechnung
Prozentsatz
ergibt:
· Grundwert = Prozentwert,
250
% · Grundwert = 5.
9
3. Schulaufgabe
MSG Würzburg
Klasse 7b
(v0.02 08.05.10)
Schuljahr 2009/2010
Also ist
Grundwert
=
18
5
5
900
=
5
·
= 18.
=
=
5
·
250
250
250
5
%
9
900
(N.B. Die Lösung wäre auch mit Hilfe der Schlussrechnung -manchmal auch
Dreisatz genannt- möglich gewesen)
(4 Punkte)
Aufgabe 6
(a) Nach der Erhöhung um 20% muss der Kunde 120% des alten
Preises zahlen, (nach der Grundgleichung der Prozentrechnung) also
120% · 36 e = 1, 2 · 36 e = 43, 20 e.
Von diesen 43,20 e (dem neuen Grundwert!!) werden wieder 10%, also
0, 1 · 43, 20 e = 4, 32 e
abgezogen.
Der Preis nach der Erhöhung und anschlieÿenden Senkung beträgt somit
43, 20 e − 4, 32 e = 38, 88 e.
(Der neue Preis lässt sich auch direkt über
90% · 120% · 36 e = 38, 88 e
berechnen.
(5 Punkte)
(b) Die Senkung um 10% bezieht sich auf einen höheren Grundwert als 36 e,
entspricht also mehr als 10% beim alten Grundwert 36 e. Frau Langer hat
also nicht nicht Recht. Die Preiserhöhung seit März beträgt insgesamt weniger
als 10%.
(Die Preiserhöhung beträgt
1, 2 · 0, 9 − 1 = 1, 08 − 1 = 0, 08 = 8%.)
(3 Punkte)
3. Schulaufgabe
Klasse 7b
(v0.02 08.05.10)
MSG Würzburg
Schuljahr 2009/2010
Gruppe B
Aufgabe 1
3 + 4 + 9 + 7 + 2 + 0 = 25. Zählt man
man: 3 · 1 + 4 · 2 + 9 · 3 + 7 · 4 + 2 · 5 =
Die Gesamtzahl der Schüler ist
alle Noten zusammen, dann bekommt
3 + 8 + 27 + 28 + 10 = 76.
Somit beträgt der Notendurchschnitt:
D = 76 : 25 = 2, 96
(Hinweis: Zum Berechnen der Division durch 25 im Kopf: Multipliziere die Zahl
zunächst mit 4 und teile dann durch 100. Durch 100 Teilchen bedeutet einfach, das
Komma um zwei Stellen nach rechts verschieben.)
(3 Punkte)
Aufgabe 2
(a) Zur Vereinfachung von
7b · 3x2 q − 7x · b2 · q − 5, 5x · qx · b
werden natürlich zuerst die Produkte vereinfacht (also Zahlen multiplizieren
und Zahl der Multiplikationen der gleichen Variablen gibt die Hochzahl; dann
noch Variablen alphabetisch ordnen), das ergibt:
7b · 3x2 q − 7x · b2 · q − 5, 5x · qx · b = 21bqx2 − 7b2 qx − 5, 5bqx2 .
Anschlieÿend können noch die gleichartigen Terme also die Terme, die bis
auf die Zahlenfaktoren übereinstimmen zusammengefasst werden, das gibt
(Gleichartige Terme werden zusammengefasst, indem man die Zahlenfaktoren
zusammenzählt und die Variablen beibehält):
21bqx2 − 7b2 qx − 5, 5bqx2 = 15, 5bqx2 − 7b2 qx.
(3 Punkte)
(b) Bei dieser Aufgabe muss man zunächst die Klammer ausmultiplizieren (alles
mit allem ) wobei die Rechenregeln für Vorzeichen zu beachten sind. Anschlieÿend
kann man wie oben die Produkte vereinfachen und dann gleichartige Terme
zusammenfassen.
− 2p(p − q) + (p2 + 3) · (5 − p2 ) + 4(p − 3)
= −2p2 + 2pq + 5p2 − p4 + 15 − 3p2 + 4p − 12
= 2pq − p4 + 3 + 4p.
(6 Punkte)
Aufgabe 3
Um die Ausgangsgleichung
3(y + 6) − y + 2 = 6y + 7 − (y + 3)
3. Schulaufgabe
MSG Würzburg
Klasse 7b
(v0.02 08.05.10)
Schuljahr 2009/2010
zu lösen, multipliziert man zunächst auf beiden Seiten die Klammern aus, und fasst
zusammen:
3y + 18 − y + 2 = 6y + 7 − y − 3
2y + 20 = 5y + 4
Jetzt formt man die Gleichung so um, dass alle Terme mit
y
auf einer Seite stehen
(zum Beispiel auf der linken Seite), dies erreicht man dadurch, dass man auf beiden
Seiten
− 5y
rechnet:
−3y + 20 = 4.
Nun rechnet man auf beiden Seiten der Gleichung
alle Terme ohne
y
−20,
um dafür zu sorgen, dass
auf der rechten Seite sind:
−3y = −16.
Zum Schluss muss man die gesamte Gleichung nur noch durch
erhält:
y=
−3
dividieren und
16
.
3
y = 16
3 auf der linken
16
16
34
10
10
2
einsetzt, erhält man: 3 · ( 3 + 6) − 3 + 2 = 3 · 3 − 3 = 34 − 3 = 30 3 ;
16
16
25
2
und für die rechte Seite 6 · 3 + 7 − ( 3 + 3) = 32 + 7 − 3 = 30 3 ,
Dann noch die Probe durchführen.
Wenn man
Seite
also stimmen linke und rechte Seite überein.
Hinweis: Die schriftliche Durchführung der Probe war für die Schulaufgabe nicht
verlangt.
Die Lösungsmenge ist somit
L = { 16
3 }.
(6 Punkte)
Aufgabe 4 Vorsicht!! Aufgrund eines Tippfehlers in der Angabe ergeben
sich unsinnige das heiÿt nicht ganzzahlige Werte für die Anzahl der
Karten in den Kategorien ... und ... !!!
Um zu ermitteln, wie viele Karten jeweils in einer Kategorie verkauft wurden,
setzt man als Unbekannte die Anzahl der verkauften Karten in einer bestimmten
Kategorie, zum Beispiel der Kategorie 1
(man kann als Variable auch die Zahl
der verkauften Karten in Kategorie 2 nehmen, dann ist die Rechnung sogar etwas
einfacher. Dies sei als Übung empfohlen. Nimmt man als Unbekannte die Zahl der
Karten in Kategorie 3, dann wird die Rechnung ziemlich kompliziert, das ist nicht
zu empfehlen.)
Wenn man mit
a
die Zahl der Karten in Kategorie 1 bezeichnet, dann ist
1
2a
die Zahl der Karten für Kategorie 2, weil hiervon halb so viele wie in Kategorie
3. Schulaufgabe
MSG Würzburg
Klasse 7b
(v0.02 08.05.10)
Schuljahr 2009/2010
1 verkauft wurden. Die Anzahl der Karten für Kategorie 3 ist halb soviel, wie in
1
·
2
|{z}
Kategorie 4 und 1 zusammen, also
1
( a + 160)
|2 {z }
. Also gilt:
halb so viel wie in Kategorie 1 und 4 zusammen
•
Anzahl Karten Kategorie 1:
a
•
Anzahl Karten Kategorie 2:
1
2a
•
Anzahl Karten Kategorie 3:
1
2
•
Anzahl Karten Kategorie 4:
160
· (a + 160)
Weil die Zahl der insgesamt verkauften Karten 1490 ist, erhält man die Gleichung:
1
1
a + a + · (a + 160) + 160 = 1490.
2
2
Diese kann man noch nach bekanntem Schema lösen (vergleiche Aufgabe 3):
1
1
a + a + a + 80 + 160 = 1490.
2
2
2a + 240 = 1490
2a = 1250
a = 625.
1
Karten in Kategorie 3 beträgt
2
1
2
· 625 = 312, 5, Die Zahl der
· (625 + 160) = 392, 5 und in Kategorie 4 wurden
Die Zahl der Karten in Kategorie 2 ist dann
wie angegeben 160 Karten verkauft.
Die Probe ergibt:
625 + 312, 5 + 392, 5 + 160 = 1490.
(7 Punkte)
Aufgabe 5
Die 5 Titel von Brasilien entsprechen
27 79 %,
also sind
27 97 ,
•
Prozentsatz:
•
Prozentwert: 5
gegeben, und der Grundwert (die Zahl aller vergebenen Titel) ist gesucht. Die
gegebenen Werte eingesetzt in die Grundgleichung der Prozentrechnung
Prozentsatz
ergibt:
· Grundwert = Prozentwert,
250
% · Grundwert = 5.
9
3. Schulaufgabe
MSG Würzburg
Klasse 7b
(v0.02 08.05.10)
Schuljahr 2009/2010
Also ist
Grundwert
=
18
5
5
900
=
5
·
= 18.
=
=
5
·
250
250
250
5
%
9
900
(N.B. Die Lösung wäre auch mit Hilfe der Schlussrechnung -manchmal auch
Dreisatz genannt- möglich gewesen)
(4 Punkte)
Aufgabe 6
(a) Nach der Erhöhung um 20% muss der Kunde 120% des alten
Preises zahlen, (nach der Grundgleichung der Prozentrechnung) also
120% · 36 e = 1, 2 · 36 e = 43, 20 e.
Von diesen 43,20 e (dem neuen Grundwert!!) werden wieder 10%, also
0, 1 · 43, 20 e = 4, 32 e
abgezogen.
Der Preis nach der Erhöhung und anschlieÿenden Senkung beträgt somit
43, 20 e − 4, 32 e = 38, 88 e.
(Der neue Preis lässt sich auch direkt über
90% · 120% · 36 e = 38, 88 e
berechnen.
(5 Punkte)
(b) Die Senkung um 10% bezieht sich auf einen höheren Grundwert als 36 e,
entspricht also mehr als 10% beim alten Grundwert 36 e. Frau Langer hat
also nicht nicht Recht. Die Preiserhöhung seit März beträgt insgesamt weniger
als 10%.
(Die Preiserhöhung beträgt
1, 2 · 0, 9 − 1 = 1, 08 − 1 = 0, 08 = 8%.)
(3 Punkte)
3. Schulaufgabe
Klasse 7b
(v0.02 08.05.10)
Punkteschlüssel:
Punkte
Note
31,537
1
2631
2
2025,5
3
1520
4
7,514,5
5
07
6
MSG Würzburg
Schuljahr 2009/2010