Kompetenzen trainieren und vertiefen

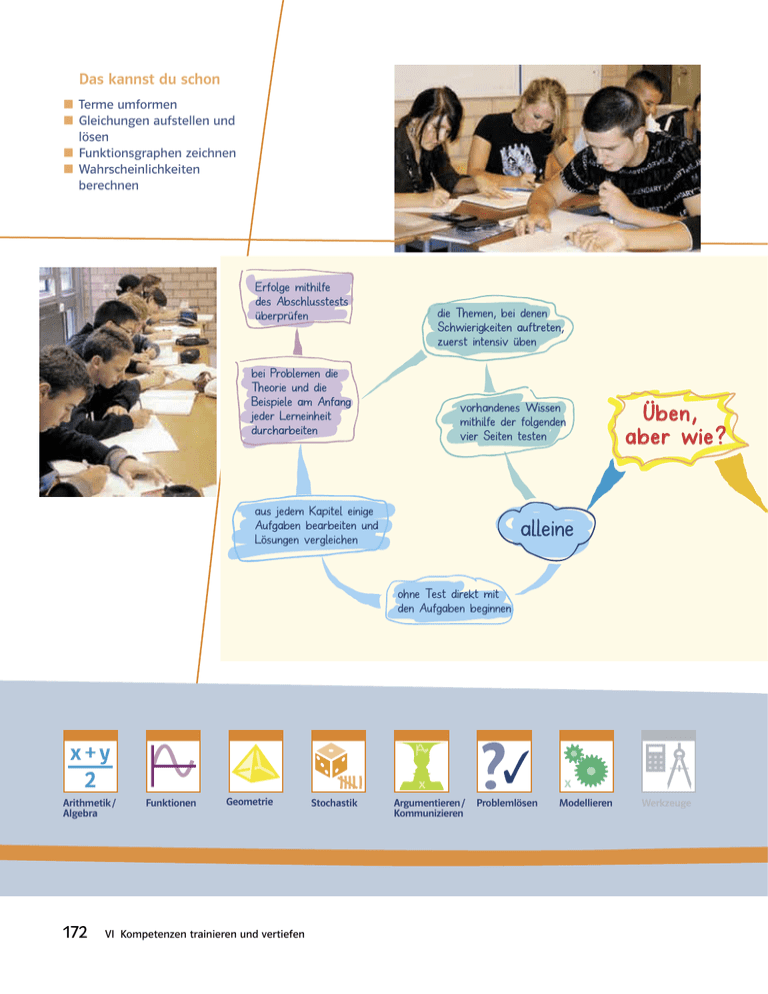
Das kannst du schon
º Terme umformen
º Gleichungen aufstellen und
lösen
º Funktionsgraphen zeichnen
º Wahrscheinlichkeiten
berechnen
Erfolge mithilfe
des Abschlusstests
überprüfen
bei Problemen die
Theorie und die
Beispiele am Anfang
jeder Lerneinheit
durcharbeiten
die Themen, bei denen
Schwierigkeiten auftreten,
zuerst intensiv üben
vorhandenes Wissen
mithilfe der folgenden
vier Seiten testen
aus jedem Kapitel einige
Aufgaben bearbeiten und
Lösungen vergleichen
Üben,
aber wie?
alleine
ohne Test direkt mit
den Aufgaben beginnen
Arithmetik /
Algebra
172
Funktionen
Geometrie
VI Kompetenzen trainieren und vertiefen
Stochastik
Argumentieren /
Kommunizieren
Problemlösen
Modellieren
Werkzeuge
VI Kompetenzen trainieren und vertiefen
Übung macht
den Meister
bei Problemen gegenseitig helfen und
die Theorie und die Beispiele am Anfang
jeder Lerneinheit durcharbeiten
pro Gruppenmitglied und pro Kapitel
mind. zwei Aufgaben bearbeiten
3-6 Personen
in einer
Gruppe
in der Klasse
Aufgaben gegenseitig
vorstellen
einige Aufgaben der Klasse
vorstellen und große
Probleme mit der ganzen
Klasse besprechen
in Kleingruppen zu jedem
Thema ein Referat halten
die vom Lehrer ausgewählten
Aufgaben bearbeiten
jedes Thema zwei bis
drei Stunden gemeinsam üben
Das kannst du bald
º sicherer mit Aufgaben umgehen
º schneller Lösungsideen finden
º bei kniffligen Aufgaben ausdauernder sein
º dich besser auf Tests vorbereiten
VI Kompetenzen trainieren und vertiefen
173
Teste dich selbst
Mithilfe der folgenden Aufgaben kannst du dich selbst testen und anschließend
einschätzen, in welchen Bereichen du bereits sicher bist und wo du noch Übungsbedarf
hast. Die Aufgaben sind nach inhaltlichen Gebieten geordnet, wie zum Beispiel dem Rechnen mit Zahlen und Variablen oder der Geometrie. In vielen Aufgaben werden neben den
inhaltlichen Themenbereichen auch deine Fähigkeiten im Argumentieren, Problemlösen
oder auch Modellieren getestet. Du musst bei jeder Aussage entscheiden, ob sie wahr
oder falsch ist, und deine Entscheidung begründen.
Auf den Seiten 251 ff.
findest du Lösungen zu
den Aufgaben.
Wahr oder falsch? Begründe.
Rechnen mit Zahlen und Variablen
1
Terme
c
d
b
a
Fig. 1
Gleichungen
Lineare Gleichungssysteme (LGS)
1
O
– 2 –1
–2
–3
1 2 3
Fig. 2
Zahlenbereiche
b)
c)
d)
f)
h)
√2
2
a) 0,5 + (2 – x) = 1 – (1 + x) besitzt die Lösung x = – 2.
b) Die Lösung y der Gleichung 4 · (y + 5) = 9 y + 5 ist ein Teiler von 15.
c) Die Lösung x von x – (x – 7) · (x + 7) = 50 – x2 ist eine einstellige Quadratzahl.
d) Die Gleichung (8 – z) · (2 + z) = (7 – z) · (z + 1) besitzt keine Lösung.
e) Die Aussage „An unserer Schule gibt es 15-mal so viele Schüler wie Lehrer“ kann
durch die Gleichung 15 · S = L ausgedrückt werden (S = Anzahl der Schüler, L = Anzahl
der Lehrer).
f) Wird eine Gleichung, die genau eine Lösung besitzt, auf beiden Seiten mit 4 multipliziert, vervierfacht sich ebenfalls die Lösung der Gleichung.
3
a) Das LGS mit 2 x – 3 y = 23 und – 2 x = y + 13 hat die Lösung x = – 2 und y = 9.
b) Wenn zwei Geraden eine unterschiedliche Steigung haben, dann besitzt das LGS aus
ihren beiden Gleichungen genau eine Lösung.
c) Die Summe der Lösungen x und y des LGS mit 2 y = 6 – 5 x und 2 x = 9 – 3 y ist 3.
d) Die Geraden in Fig. 2 veranschaulichen das LGS mit 7 x + 10 y = 3 und 2 x + 5 y = 3.
e) Ein LGS mit zwei Gleichungen und zwei Unbekannten hat entweder genau eine oder
unendlich viele Lösungen.
f) Man sieht, ohne zu rechnen, dass das LGS mit y = 3 x – 5 und y = – 2 x – 5 als einzige Lösung x = 0 und y = – 5 besitzt.
g) Ein LGS mit drei Gleichungen und zwei Unbekannten kann auch genau zwei Lösungen besitzen, da drei Geraden sich ja auch genau zweimal schneiden können.
4
b)
c)
d)
e)
174
a) 5x – 2 = 3 x
Die blaue Fläche in Fig. 1 lässt sich berechnen mit dem Term (a – b) · (c + d).
Die blaue Fläche in Fig. 1 lässt sich berechnen mit dem Term a · (d + c) – b d – b c.
(3 – x)2 = 9 – x2
e) a2 – a = a
____
x · 4__x + 5 x__= x · 9 x__ = 9 x2
g) 9a2 + b2__= a + b
2__
5 √3 – 2 √3 = 3 √3
i) _
= √2
a) Eine Dezimalzahl, die unendlich viele Nachkommastellen hat, ist immer irrational.
Ein Bruch, bei dem der Nenner ein Teiler des Zählers ist, ist immer eine ganze Zahl.
Das Produkt von 789 negativen Zahlen ist immer negativ.
Das Produkt von zwei echten Brüchen ist immer ein echter Bruch.
Das Produkt von drei irrationalen Zahlen ist immer irrational.
VI Kompetenzen trainieren und vertiefen
Funktionen
5
5
a) _8 = 62,5 %
b) 7 % von 12 700 Menschen sind 889 Menschen.
c) Eine um 30 % reduzierte Hose, die jetzt 49 € kostet, hat zuvor 69 € gekostet.
d) Wenn ein MP3-Player inklusive 19 % Mehrwertsteuer 84,49 € kostet, dann kostet er
ohne Mehrwertsteuer 68,44 €.
e) Legt man 4500 € für vier Monate zu einem Zinssatz von 3 % an, so erhält man nach
den vier Monaten 4635 € ausgezahlt.
f) Max behauptet: „Wenn die Bank A 2 % und die Bank B 4 % Zinsen pro Jahr zahlt, bekommt man nach zehn Jahren für x Euro bei der Bank B doppelt so viele Zinsen ausgezahlt wie bei der Bank A.“
6
Prozent- und Zinsrechnung
a) Wenn drei Liter Milch 1,77 € kosten, dann kosten fünf Liter Milch 2,95 €.
b) Wenn fünf Musiker zum Spielen eines Stückes zwölf Minuten brauchen, dann brauchen 15 Musiker zum Spielen dieses Stückes nur vier Minuten.
c) Wenn ein Heuvorrat für zwölf Pferde sechs Tage reicht, dann reicht er für acht Pferde
zehn Tage.
d) Die Zuordnung „Dicke eines Buches“ ¥ „Preis eines Buches“ ist proportional.
e) Jede Gerade ist der Graph einer proportionalen Zuordnung.
f) Die Gleichung y = _3x gehört zu einer antiproportionalen Zuordnung, deren Graph in
Fig. 1 dargestellt ist.
Zuordnungen
y
7
Geraden
b)
c)
d)
e)
f)
g)
a) Der Punkt (4 | 3) liegt auf der Geraden mit der Gleichung y = 3 x – 5.
Die Gerade in Fig. 2 besitzt die Gleichung y = 0,6 x + 1.
Die Gerade durch die Punkte S (3 | – 1) und T (2 | – 5) besitzt die Gleichung y = – 6 x + 17.
Die Gerade mit der Gleichung x = 3 verläuft parallel zur y-Achse.
Die Gerade mit y = 3 x + 5 verläuft steiler als die Gerade mit y = 2 x + 7.
Jede lineare Funktion schneidet genau einmal die x-Achse und einmal die y-Achse.
Die Geraden g und h mit g: y = 4 x – 6 und h: y = 4 x – 5 schneiden sich in S (4 | – 1).
3
2
1
x
O
–3 – 2 –1
1 2
Fig. 1
y
3
2
1
–3 – 2 –1O
x
1 2
Fig. 2
Geometrie
8 a) Beträgt einer von zwei Nebenwinkeln bei zwei sich schneidenden Geraden 90°, so
schneiden sich die beiden Geraden im rechten Winkel.
b) Kennt man in einem Parallelogramm zwei Winkel, so lassen sich die anderen beiden
berechnen.
c) Es gibt ein Viereck mit drei rechten Winkeln, welches kein Rechteck ist.
d) Wenn ein Winkel viermal so groß ist wie sein Nebenwinkel, dann beträgt der Nebenwinkel 36°.
9 a) Kennt man zwei Innenwinkel eines Dreiecks, lässt sich der dritte berechnen.
b) Kennt man die drei Winkel eines Dreiecks, lässt es sich eindeutig konstruieren.
c) Ein Dreieck mit a = 3 cm, b = 5 cm und c = 35° lässt sich eindeutig konstruieren.
d) Ein Dreieck mit a = 5 cm, b = 7 cm und c = 13 cm lässt sich eindeutig konstruieren.
e) Es gibt keine gleichseitigen rechtwinkligen Dreiecke.
f) Der Schnittpunkt der Mittelsenkrechten liegt immer innerhalb des Dreiecks.
g) Ist die längste Seite eines Dreiecks Durchmesser seines Umkreises, so benötigt man
einen an diese Seite angrenzenden Innenwinkel, um die anderen berechnen zu können.
Winkelbeziehungen
Dreiecke
C
c
a
b
b
a
A
c
VI Kompetenzen trainieren und vertiefen
B
Fig. 3
175
10
Vierecke
D
d
c
d
c
C
b
A a
a
b
B
Fig. 1
a) Ein Viereck mit a = 3 cm, b = 5 cm, c = 65° und d = 100° lässt sich eindeutig konstruieren.
b) Ein gleichschenkliges Trapez mit a parallel zu c und a = 6 cm, c = 3,5 cm und mit der
zu a gehörigen Höhe ha = 2 cm lässt sich eindeutig konstruieren.
c) Jedes Rechteck ist ein Trapez.
d) Jedes Parallelogramm ist eine Raute.
e) Jedes achsensymmetrische Viereck ist ein gleichschenkliges Trapez.
Flächeninhalte
11
Körper
12
a) Ein rechtwinkliges Dreieck mit den Seitenlängen a = 3 cm, b = 5 cm und c = 6 cm
besitzt einen Flächeninhalt von 15 cm2.
b) Ein Quadrat mit der Seitenlänge 5 cm besitzt einen größeren Flächeninhalt als ein Trapez mit den parallelen Seiten a = 7 cm, c = 3 cm und der Höhe h = 5 cm.
c) Ein Parallelogramm mit den Seiten a = 2 cm und b = 5 cm, das kein Rechteck ist, besitzt den Flächeninhalt 10 cm2.
d) Stimmen in zwei Vierecken alle vier Seiten überein, so sind ihre Flächeninhalte gleich.
e) Ein Kreis mit dem Radius r = 3 cm besitzt einen Flächeninhalt von etwa 28,3 cm2.
f) Verdoppelt sich der Radius eines Kreises, verdoppelt sich auch sein Flächeninhalt.
Fig. 2
a) Ein Prisma mit Grundfläche 12 cm2 und Höhe 3 cm besitzt ein Volumen von 36 m3.
b) Die Schokoladenverpackung in Fig. 2 ist ein Prisma.
c) Ein Zylinder mit dem Radius r = 5 cm und der Höhe h = 2 cm besitzt ein Volumen von
etwa 137,1 cm3.
d) Verdoppelt man die Seitenlängen eines Würfels, verachtfacht sich sein Volumen.
e) Wenn man eine 1-Liter-Milchverpackung würfelförmig machen will, dann müsste jede
Seite 10 cm lang sein.
f) Ein Körper mit vier Flächen kann kein Prisma sein.
Daten und Zufall
13
Wahrscheinlichkeiten
Fig. 3
Statistik
176
a) Die Wahrscheinlichkeit, mit einem Würfel eine gerade Zahl zu würfeln, ist 0,5.
b) Die Wahrscheinlichkeit, mit einem Quader (Fig. 3) eine gerade Zahl zu würfeln, ist 0,5.
c) Die Wahrscheinlichkeit, in zwei Münzwürfen zweimal „Zahl“ zu werfen, ist genauso
groß wie die Wahrscheinlichkeit, in zwei Münzwürfeln einmal „Zahl“ und einmal „Wappen“
zu werfen.
d) Das Gegenereignis zu „eine Zahl kleiner als drei würfeln“ ist das Ereignis „eine Zahl
größer als drei würfeln“.
e) Wahrscheinlichkeiten und relative Häufigkeiten sind das Gleiche, beide werden in Prozent angegeben.
f) Die Wahrscheinlichkeit für „dreimal hintereinander eine 5 würfeln“ ist genauso groß
wie die Wahrscheinlichkeit für „in drei Würfen die Summe 15 würfeln“.
14
a) Der Median der Datenreihe 2, 8, 5, 3, 2, 6, 7, 4, 5 ist 4.
26
b) Das arithmetische Mittel der Datenreihe 2, 8, 5, 3, 2, 6, 7, 4, 5 ist _
6.
c) Wird von 200 Würfen 34-mal die „6“ gewürfelt, beträgt ihre relative Häufigkeit 34 %.
d) Hat eine Datenreihe nur gleiche Werte, so ist ihr Mittelwert gleich diesem Wert.
e) Zu den Wahlergebnissen einer Bundestagswahl lässt sich weder der Median noch das
arithmetische Mittel bestimmen.
f) Ist das arithmetische Mittel einer Datenreihe aus fünf Daten 3, so muss die Summe
aller Daten 15 sein.
VI Kompetenzen trainieren und vertiefen
a)
b)
c)
d)
e)
f)
Lies aus dem Boxplot ab, ob die folgenden Aussagen wahr oder falsch sind.
Das langsamste Mädchen ist langsamer als jeder Junge.
50 % der Jungen laufen zwischen 8,6 und 9,5 Sekunden.
Bei den Mädchen laufen vermutlich mehr als 50 % zwischen 8,6 und 9,5 Sekunden.
Die beste Zeit aus dem Jahrgang ist ein Mädchen gelaufen.
Der langsamste Junge lief über 10 Sekunden.
Die besten 25 % der Jungen liefen schneller als 8,6 Sekunden.
Diagramme
Zeit in s
15
10,5
10,0
9,5
9,0
8,5
8,0
w
m
Geschlecht
Boxplot zu den Sprintergebnissen über 50 m.
Auswertung und Selbsteinschätzung
Vergleiche deine Ergebnisse mit den Lösungen und Begründungen auf den Seiten 251
und folgende. Jetzt weißt du, wie viele Fragen du richtig beantwortet und begründet hast,
und kannst einschätzen, wie sicher du in den verschiedenen Gebieten der Mathematik
bist. Notiere in deinem Heft die folgenden Aussagen und beurteile deine Fähigkeiten zu
den genannten Inhalten mithilfe der Noten von 1 bis 6. Eine „1“ heißt, dass du den aufgeführten Inhalt sehr gut beherrschst, und eine „6“, dass du ihn gar nicht beherrschst.
1.
2.
3.
4.
5.
Ich kann Terme mit Variablen aufstellen und sicher umformen.
Ich kann Flächen verschiedenen Termen zuordnen.
Ich kann Wurzelterme sicher vereinfachen.
Ich beherrsche die Prozent- und Zinsrechnung sicher.
Ich kann proportionale und antiproportionale Zuordnungen in Form einer Wertetabelle,
eines Graphen oder einer Gleichung darstellen.
6. Ich kann Aufgaben mit dem Dreisatz sicher lösen.
7. Ich kann Funktionsgleichungen aufstellen und zugehörige Graphen zeichnen.
8. Ich kann Gleichungen und lineare Gleichungssysteme sicher lösen.
9. Ich kann fehlende Winkel in geometrischen Figuren sicher bestimmen.
10. Ich kann Planskizzen anfertigen und Dreiecke und Vierecke exakt konstruieren.
11. Ich kenne alle wichtigen Eigenschaften von Dreiecken und besonderen Vierecken.
12. Ich kann Flächen und Volumina berechnen.
13. Ich kann Wahrscheinlichkeiten und relative Häufigkeiten sicher berechnen.
14. Ich kenne den Unterschied zwischen Median und Mittelwert und kann beides bestimmen.
15. Ich kann Kreisdiagramme, Säulendiagramme und Boxplots zeichnen und interpretieren.
Jetzt kannst du mit dem Üben beginnen. Auf den Seiten 172 und 173 findest du Vorschläge, wie du dabei vorgehen kannst. Begleite deine Übungsphasen am besten mit einem
Lernprotokoll. Die folgende Tabelle bietet dir eine Hilfestellung, wie du ohne viel Aufwand
ein solches Lernprotokoll führen kannst, welches deinen Lernprozess begleitet und unterstützt.
Mein Lernprotokoll
Thema
Aufgabe
alleine
bearbeitet
(j/n)
richtig/
falsch
Was fand ich
an der Aufgabe
schwierig?
Rechnen mit Zahlen
und Variablen
Funktionen
Geometrie
Stochastik
Du kannst dir natürlich
noch eigene Aussagen
zur Selbsteinschätzung
überlegen. Diese Aussagen sollen nur eine
Anregung sein.
Üben – aber wie?
Hole dir Hilfen und
Anregungen auf den
Seiten 172 und 173.
Muss ich derartige Aufgaben noch mehr üben?
VI Kompetenzen trainieren und vertiefen
177
1 Arithmetik und Algebra
In der Arithmetik und Algebra geht es um das Rechnen mit Zahlen und Variablen.
Auch das Aufstellen, Umformen und Lösen von Gleichungen sowie linearen Gleichungssystemen ist ein wichtiger Bestandteil der Algebra.
Zahlenbereiche
Natürliche Zahlen (N): 1, 2, 3, 4, 5, …
Ganze Zahlen (Z): … – 3; – 2; – 1; 0; 1; 2; 3; …
Rationale Zahlen (Q): Alle Zahlen, die sich als Bruch darstellen lassen. (Jede endliche und
jede periodische Dezimalzahl lässt
__ sich ebenfalls als Bruch darstellen.)
Irrationale Zahlen: Zahlen wie √2 = 1,414 213 56 …, die sich nicht als Bruch schreiben
lassen. Man kann diese Zahlen nur näherungsweise und nicht exakt als Dezimalzahlen
angeben, denn die zugehörigen Dezimalzahlen haben unendlich viele Nachkommastellen
und sind nicht periodisch.
Reelle Zahlen (R): Alle rationalen und irrationalen Zahlen.
Wurzeln
Die Schreibweise √2 ; √3,5 ; √__4 usw. meint jeweils diejenige positive Zahl, deren Quadrat 2; 3,5; 4 usw. ergibt. Zu √2 sagt man Quadratwurzel aus 2 oder einfach Wurzel
aus 2. Viele Wurzeln sind irrationale Zahlen und lassen sich daher als Dezimalzahl nicht
exakt angeben.
__
__
___
__
____
Beispiele √9 = 3; √0,25 = 0,5;
__
16
_
49
___
√
__
__
= _47 ; √232 = 23; 9 x2 = x (für x > 0); √5 = 2,236 067 97…
Rechengesetze
Kommutativgesetze (Vertauschungsgesetze):
Für zwei Zahlen a und b gilt:
a + b = b + a und a · b = b · a
Assoziativgesetze (Verbindungsgesetze):
Für drei Zahlen a, b und c gilt: (a + b) + c = a + (b + c) und (a · b) · c = a · (b · c)
Distributivgesetze (Verteilungsgesetze):
Für vier Zahlen a, b, c und d gilt: a · (b + c) = a b + a c und a · (b – c) = a b – a c
bzw. (a + b) · (c + d) = a (c + d) + b (c + d) = a c + a d + b c + b d
„Vorfahrtsregeln“
In Termen müssen Klammern zuerst berechnet werden, und zwar die innere vor der äußeren. Außerdem gilt: Punktrechnung vor Strichrechnung.
Beispiele a) – x · 2 – 9 x2 + (2x)2 3
= – x · 2 – 9 x2 + 4 x2 3
= – x · 2 – 5 x2 3 = 5 x3
binomische Formeln
b) (2 a + 3) · (4 a – 7) – 8 a2
= 8 a2 – 14 a + 12 a – 21 – 8 a2
= – 2 a – 21
Es gelten drei binomische Formeln:
1. (a + b)2 = a2 + 2 a b + b2
2. (a – b)2 = a2 – 2 a b + b2
Beispiele a) (x + 3)2 = x2 + 6 x + 9
b) (s + 2 t) · (s – 2 t) = s2 – 4 t2
Rechnen mit Wurzeln
178
3. (a + b) · (a – b) = a2 – b2
c) (a – 4 b)2 = a2 – 8 a b + 16 b2
d) x2 + 10 x y + 25 y2 = (x + 5 y)2
Für a,__ b º __0 gilt:____
a) √a · √b = √a · b
b) √a : √b = √a : b
Beispiele
__
__
__
a) √2 · √8 = √16 = 4
b) √27 : √3 = √27 : 3 = √9 = 3 c) √200 = √100 · √2 = 10 √2
VI Kompetenzen trainieren und vertiefen
__
__
__
__
____
_____
c)
__
___
__
___
___
__
__
√a2b = √a2 · √b = a √b
__
__
Zur Berechnung der Lösung einer Gleichung mit einer Variablen muss die Gleichung mittels der für Terme und Gleichungen geltenden Regeln nach dieser Variablen aufgelöst werden, sodass sie nach der Umformung alleine auf einer Seite des Gleichheitszeichens steht.
Gleichungen
Beispiel 8 x – 2 (x – 1) = 8 + 3 x
8x – 2x + 2 = 8 + 3x
6x + 2 = 8 + 3x
| –3x
3x + 2 = 8
| –2
3x = 6
|:3
x=2
Zur Kontrolle der Ergebnisse kann man die
Lösung in die erste Zeile
einsetzen. Wenn eine
wahre Aussage rauskommt, ist das Ergebnis
richtig.
Zur Probe x = 2 in die Ausgangsgleichung
einsetzen: 8 · 2 – 2 (2 – 1) = 8 + 3 · 2
16 – 2 · 1 = 8 + 6
14 = 14
14 = 14 ist eine wahre Aussage, also ist x = 2
die Lösung der Gleichung.
Zum Lösen von linearen Gleichungssystemen mit zwei Variablen gibt es drei Verfahren:
das Gleichsetzungsverfahren, das Einsetzungsverfahren und das Additionsverfahren.
Beispiele
Gleichsetzungsverfahren
I: y = 5 x + 2 und
II: y = x – 6
I und II gleichsetzen:
5x + 2 = x – 6 | –x
4x + 2 = –6
| –2
4x = –8
|:4
x = –2
x = – 2 in I (oder II)
einsetzen:
y = 5 · (– 2) + 2 = – 8
(– 2 | – 8) ist die Lösung
des LGS.
Einsetzungsverfahren
I: y = – 3 x + 1 und
II: 3 x – 2 y = 25
I in II einsetzen:
3 x – 2 (– 3 x + 1) = 25
3 x + 6 x – 2 = 25
9 x = 27
x=3
x = 3 in I einsetzen:
y = – 3 · (3) + 1 = – 8
(3 | – 8) ist die Lösung
des LGS.
Lineare Gleichungssysteme (LGS) mit zwei
Variablen
Additionsverfahren
I: 4 x + 2 y = 8 und
II: 6 x – 2 y = 2
I und II addieren:
10 x = 10
| : 10
|+2
x=1
|:9
x = 1 in I (oder II) einsetzen:
4·1 + 2y = 8
y=2
(1 | 2) ist die Lösung
des LGS.
Aufgaben
1
Setze Klammern so, dass das Ergebnis stimmt.
a) – 28 – 21 : 7 = – 1
b) 3 · 5 + 9 · (– 2) = – 48
c) (– 2) · 14 – 4 · 5 = – 100
2
Die blaue Fläche in Fig. 1 lässt sich auf verschiedene Weisen berechnen.
a) Elisa gibt für die Berechnung der blauen Fläche den folgenden Term an:
(x – b) (y – a) + a (x – b) + b (y – a).
Zeichne die Fig. 1 als Skizze in dein Heft und teile die blaue Fläche entsprechend Elisas
Term ein. Erkläre in Worten, wie Elisa auf diesen Term kommt.
b) Finde zwei weitere Terme, mit denen sich die blaue Fläche berechnen lässt.
c) Zeige durch eine Rechnung, dass Elisas und deine beiden Terme äquivalent sind.
b
a
y
x
Fig. 1
3
Welche Zahlen kannst du für a und b einsetzen, sodass die Rechnung stimmt? Finde
jeweils mindestens zwei Möglichkeiten.
_____
____
__
– a2
√
√
√
a) a : b = 3
b) a · b = 3
c) _
=
3
d)
3
·
a
=
b
e)
3
a
=
b
f)
a2 · b = 3
b
4
Fabian behauptet: „Ich habe alle Rekorde gebrochen. In zwei Stunden habe ich 15 202
Purzelbäume geschlagen.“ Elisabeth glaubt ihm nicht. Kann Fabians Behauptung stimmen? Begründe durch Rechnung.
VI Kompetenzen trainieren und vertiefen
179
5
Phillip arbeitet in einer Fahrradwerkstatt und ist dafür zuständig, die Rechnungen für
die Kunden in Excel zu schreiben. Eine unvollständige Rechnung ist in Fig. 1 abgebildet.
1
3
4
5
6
7
8
9
10
12
A
B
Rechnung Nr. 9876
Artikel
Schutzblech
Bremsschuh
Pedale
Kette
Gepäckträger
C
Datum: 23. 11. 2007
D
1
Menge
Einzelpreis (€) Gesamtpreis (€)
2
5,99
11,98
4
4,58
2
32,98
1
29,95
29,95
1
31,95
31,95
Zwischensumme
MwSt. (%)
19
Rechnungsbetrag
148,96
3
4
5
6
7
8
9
10
A
B
Rechnung Nr. 9876
Artikel
Schutzblech
Bremsschuh
Pedale
Kette
Gepäckträger
C
Datum: 23. 11. 2007
D
Menge
Einzelpreis (€) Gesamtpreis (€)
2
5,99
= B4*C4
4
4,58
16,49
2
1
29,95
= B7*C7
1
31,95
Zwischensumme
MwSt. (%)
19
Rechnungsbetrag
12
Fig. 1
Fig. 2
a) Berechne die fehlenden Werte in der Tabelle (Fig. 1). Schreibe z. B.: D5 =…
b) Phillip berechnet die Werte in Spalte D mithilfe von Excel. In Fig. 2 siehst du zwei seiner Eingaben. Ergänze mögliche Formeln zur Berechnung der fehlenden Beträge in Fig. 2
und kontrolliere mit dem Taschenrechner, ob deine Formel stimmen kann.
6
Entscheide, ob die folgenden Aussagen wahr oder falsch sind. Begründe.
a) Jede natürliche Zahl lässt sich als Bruch schreiben.
b) Subtrahiert man zwei natürliche Zahlen, erhält man immer eine natürliche Zahl.
c) Multipliziert man zwei irrationale Zahlen, erhält man immer eine irrationale Zahl.
d) Da Wurzeln immer positiv sind, gibt es keine negativen irrationalen Zahlen.
e) Es gibt irrationale Zahlen, deren 1000-Faches eine rationale Zahl ist.
f) Addiert man fünf aufeinander folgende natürliche Zahlen miteinander, ist das Ergebnis
immer ein Vielfaches der Zahl 5.
7
1
Auf dem Foto (Fig. 3) siehst du etwa _
40
der Besucher eines Konzertes von Herbert
Grönemeyer. Schätze die Anzahl der Konzertbesucher. Erläutere dein Vorgehen.
8
Hinweis:
Zum Überprüfen musst
du für jede Variable
eine Zahl in die Aufgabe und in dein Ergebnis
einsetzen.
Es muss jeweils das
Gleiche herauskommen.
a)
b)
c)
d)
e)
Vereinfache so weit wie möglich.
3 x · 4 y + 2 x (5 – y)
4 (3 a – 7 b) – 7 (4 b – 3 a) + 3 (7 a – 4 b)
72 x y – 2 (4 y – (7 y – 6 x)) · (– 12 x)
4 x 2 x - x2 + (3 x)3 3 – (5 x - 4) · (5 x + 4)
Überprüfe deine Ergebnisse.
nen 1, 2, 6 und 12 herauskommt.
a) Welcher Term gehört zu welchem Wert?
Jeder untersucht ohne Taschenrechner zwei
Terme und stellt seinem Tischnachbarn die
Rechnungen vor.
b) Konstruiert selbst einen komplizierten
Term mit einem einfachen Ergebnis und
notiert den Term und das Ergebnis auf
zwei Seiten eines Kärtchens. Nutzt die
Kärtchen als Übungsmaterial.
180
Fig. 3
9 p Robert hat Terme aufgestellt, bei de-
VI Kompetenzen trainieren und vertiefen
__
___
i)
___
3 √48 + __
6 √108
___
___
2 √6 + √24
– √54
__
___
√6
___
2 √12
___
iii)
ii)
__
___
__
√
108 – 2 √48
+ 2 √75
__
___
2 √12
__
__
√18 3
√16 2 √__27 + __
iv) ___
2 √2 + √12
10
Pollys Tipp:
11
Tipp: Achte auf die
richtige Klammersetzung. Setze nach jedem
Schritt eine Klammer
um das „neue“ Ergebnis.
Denke dir eine beliebige Zahl. Verdopple diese Zahl und addiere anschließend 7. Multipliziere das Ergebnis mit 3 und addiere anschließend 3. Multipliziere das Ergebnis erneut mit 3 und subtrahiere vom Ergebnis die Summe aus deiner anfangs gedachten Zahl
und 4. Teile das Ergebnis durch 17 und subtrahiere erneut deine anfangs gedachte Zahl.
a) Führe die Anweisungen für drei verschiedene Zahlen durch. Was fällt auf?
b) Schreibe für deine anfangs gedachte Zahl die Variable x und stelle einen Term auf, der
zu den Anweisungen passt.
c) Vereinfache den Term aus b) so weit wie möglich und begründe die Entdeckung aus a).
d) p Denke dir selbst ein ähnliches Rätsel aus und lasse es von deinem Nachbarn lösen.
Finde heraus, wie viele Hölzchen in den blauen bzw. roten Boxen sind, sodass auf
beiden Seiten einer Gleichung gleich viele Hölzchen liegen. Achte darauf, dass in jeder
blauen bzw. roten Box innerhalb einer Aufgabe gleich viele Hölzchen liegen müssen.
a) i)
b) i)
ii)
=
=
ii)
=
=
und
und
=
=
12
Eine vierköpfige Familie ist zusammen 127 Jahre alt. Das ältere Kind ist halb so alt
wie die Mutter. Die Mutter ist drei Jahre jünger als der Vater. Das jüngere Kind ist zwei
Jahre jünger als das ältere. Wie alt sind die Familienmitglieder?
13
Frau Klein hat typische Fehler der Klassenarbeit aufgeschrieben. Finde und korrigiere
sie. Führe nach deiner Korrektur jeweils die Probe durch.
a) 18 x + 6 = 14 x – 4 |– 14 x
4x + 6 = –4
|– 6
4 x = – 10
|– 4
x = – 14
b) 9 (3 + 2 x) = – 1
27 + 2 x = – 1
2 x = 26
x = 13
c) (x + 4)2 + (x – 6)2 = 2 x2 + x
x2 + 16 + x2 – 36 = 2 x2 + x
2 x2 – 20 = 2 x2 + x
– 20 = x
|– 27
|: 2
|– 2 x2
14
Die Seitenlängen eines Rechtecks unterscheiden sich um 2 cm. Verkürzt man die
kürzere Seite um 5 cm und verlängert gleichzeitig die längere Seite um 3 cm, so wird der
Flächeninhalt um 55 cm2 kleiner. Wie lang sind die Seiten des ursprünglichen Rechtecks?
2
3
Gegeben sind die Gleichungen I. 4 x = y und II. 6 x – _61 = y.
a) Löse das lineare Gleichungssystem rechnerisch.
b) Zeichne die Geraden zu I und II in ein Koordinatensystem und überprüfe deine Lösung
aus a) zeichnerisch.
c) x soll der Zeit in Stunden und y der zurückgelegten Strecke beim Wandern in Kilometern entsprechen. Erfinde eine zu den Gleichungen passende Aufgabe.
d) Was bedeutet die in a) berechnete Lösung im Sachzusammenhang der Aufgabe aus c)?
15
16
Gib je ein LGS mit zwei Variablen an, das die angegebene Lösung hat.
a) (1 | 2)
b) (0 | – 4)
c) (5 | – 6)
d) (– 3 | – 1)
VI Kompetenzen trainieren und vertiefen
181
2 Funktionen
Zuordnungen oder Funktionen beschreiben Zusammenhänge von Größen mithilfe
von Tabellen, Graphen und Gleichungen. Dabei werden die Zuordnungen bzw. Funktionen
oft zum Modellieren, also zum Beschreiben der Wirklichkeit, eingesetzt.
23
Der Ausdruck 23 % ist eine andere Schreibweise für _
100 oder 0,23.
Prozentrechnung
Für den Prozentsatz gilt: Prozentsatz p =
Prozentwert W
Grundwert G
__
W
oder kurz p = _
G.
Beispiel
Von 25 Schülern (Grundwert G) haben 7 Schüler (Prozentwert W) eine Drei in der Mathe28
7
_
matikarbeit. Das sind p = _
25 = 100 = 0,28 = 28 % der Schüler.
Um W oder G zu bestimmen, löst man die Formel für p nach der gesuchten Größe auf:
Formel
Bauernregeln
Beispiel
W
p·G
Bauernregel:
Durch Abdecken der gesuchten Größe lässt sich
dem Dreieck die nötige
Formel entnehmen.
W
p=_
G
W = p·G
p=
|·G
|:p
W
G=_
p
W
p · G
G=
7
0,28 = _
25
W
p · G
| · 25
7 = 0,28 · 25
W=
W
p · G
| : 0,28
7
25 = _
0,28
Jahreszins: Wenn man ein Guthaben G für ein Jahr zu einem Zinssatz p bei der Bank anlegt, erhält man nach Ablauf des Jahres G · p Zinsen.
Tageszins: Legt man das Guthaben G nicht für das ganze Kalenderjahr, sondern nur für t
t
Tage an, so erhält man nur _
360 · G · p Zinsen.
Zinseszins: Liegt ein Guthaben G für x Jahre zu einem Zinssatz p auf der Bank, so kann
man das Kapital K nach x Jahren so berechnen: K = (1 + p)x · G
Zinsrechnung
Beispiel
Tim legt 2300 € zu einem Zinssatz von 3 % an. Legt er sein Geld ein Jahr an, erhält er
150
2300 € · 0,03 = 69 € Zinsen. Legt er es 5 Monate an, erhält er _
360 · 69 € = 28,75 €. Legt
4
er es vier Jahre an, hat er ein Kapital von (1 + 0,03) · 2300 € ≈ 2588,67 €.
2 3
proportionale
Zuordnung
Jede proportionale Zuordnung ist eine spezielle lineare Funktion.
Bei einer proportionalen Zuordnung x ¥ y gehört zum 2-; 3- bzw. n-Fachen der Größe
x auch das 2-; 3- bzw. n-Fache der Größe y. Der y-Wert lässt sich mit einer Gleichung der
Form y = m · x berechnen. Der Graph einer proportionalen Zuordnung ist eine Gerade,
die immer durch den Punkt (0 | 0) verläuft.
Ursprungsgerade
y
2
1
O
0,5
0,5
0,5
1 2 3 4
x
Fig. 1
antiproportionale
Zuordnung
182
Beispiel
Durch die Tabelle in Fig. 2 wird eine proportionale Zuordnung beschrieben.
Die Zuordnungsvorschrift lautet y = 0,5 · x.
Der Graph ist in Fig. 1 dargestellt.
·2
X
1
Y
0,5
·2
·5
2
3
5
7
10
1
1,5
2,5
3,5
5
·5
Fig. 2
Bei einer antiproportionalen Zuordnung x ¥ y gehört zum 2-; 3-; bzw. n-Fachen der Größe
x der 2-te; 3-te; bzw. n-te Teil der Größe y. Der y-Wert lässt sich mit einer Gleichung der
a
Form y = _x berechnen. Der Graph einer antiproportionalen Zuordnung ist eine Hyperbel.
VI Kompetenzen trainieren und vertiefen
Beispiel
Durch die Tabelle in Fig. 1 wird eine antiproportionale Zuordnung beschrieben. Die
Zuordnungsvorschrift lautet y = _4x .
Der Graph ist in Fig. 2 dargestellt.
X
0,4
0,5
1
Y
10
8
4
2
4
5
2
1
0,8
:2
Achtung!
Hier teilen!
Jede antiproportionale
Zuordnung ist eine spezielle Funktion.
·5
·2
Hyperbel
:5
Fig. 1
Bei einer proportionalen sowie bei einer antiproportionalen Zuordnung lassen sich gesuchte Werte mit dem Dreisatz bestimmen:
Beispiel (proportional)
1200 ø Heizöl kosten 600 €. Mit dem Dreisatz lässt sich berechnen, wie viel 1700 ø
Heizöl kosten:
Heizölmenge in ø
Preis in ¤
1200
600
1
0,5
1700
850
: 1200
· 1700
Beispiel (antiproportional)
Eine Packung Vogelfutter reicht für drei
Vögel 15 Tage. Mit dem Dreisatz lässt sich
berechnen, wie viele Tage die Packung für
fünf Vögel reicht:
Anzahl der Vögel
:3
3
15
·3
· 1700
·5
1
45
:5
5
9
Zuordnungen x ¥ y, bei denen man zur Berechnung des y-Wertes eine Gleichung der
Form y = m · x + n aufstellen kann, heißen lineare Funktionen.
Der Graph schneidet die y-Achse in S (0 | n), wobei n y-Achsenabschnitt genannt wird. Die
Steigung m gibt an, um wie viel der y-Wert steigt bzw. fällt, wenn x um 1 zunimmt.
Beispiel
Die Gerade g geht durch die Punkte A (1 | 5)
und B (– 1 | – 1). Die Steigung m von g lässt
sich berechnen mit:
m=
yB – yA
xB – xA
_
=
–_
1–5
–1 – 1
–6
=_
–2 = 3
Durch das Einsetzen von m = 3 und den
Koordinaten eines Punktes, z. B. A (1 | 5) in
y = m · x + n, lässt sich n berechnen:
5 = 3·1 + n |–3
n=2
Die Funktionsgleichung von g ist also:
y = 3 x + 2.
y
7
6
5
4
3
y-Achsenab2
schnitt n = 2
1
–4 –3 – 2 – 1
B
–2
O
1 2 3 4
x
Fig. 3
Achtung! Auf der
einen Seite wird multipliziert und auf der
anderen dividiert!
Anzahl der Tage
: 1200
y
4
3
2
1
Lineare Funktionen
g
A
3 Einheiten
nach oben
1 Einheit
nach rechts
Also ist
m=3:1=3
und damit
g: y = 3 x + 2
1 2 3 4 5 6 7 8
x
Aufgaben
1
20 % aller Nordrhein-Westfalen waren noch nie in den Niederlanden. Welche von den
folgenden Aussagen bedeutet das Gleiche? Kommentiere deine Antwort.
(I) Jeder zwanzigste Nordrhein-Westfale war noch nie in den Niederlanden.
(II) 20 Nordrhein-Westfalen waren noch nie in den Niederlanden.
(III) Von 15 Nordrhein-Westfalen waren durchschnittlich drei noch nie in den Niederlanden.
(IV) Von zwanzig Nordrhein-Westfalen war durchschnittlich einer noch nie in den Niederlanden.
(V) Jeder fünfte Nordrhein-Westfale war noch nie in den Niederlanden.
VI Kompetenzen trainieren und vertiefen
183
2
Bank A:
– 3,5 % Zinsen in
den ersten beiden
Jahren
– ab dem dritten
Jahr 4,5 % Zinsen
Bank B:
– 4 % Zinsen
– bei Anlagezeiten
unter einem Jahr
werden 10 € Bearbeitungsgebühr
erhoben
Strecke
in km
Verbrauch
in Litern
80
6,4
150
12
180
14,4
260
20,8
Fig. 1
Antonia erzählt Helene: „Ich habe für meine neuen Schuhe nur noch 39 € bezahlt und
habe dabei 40 % gespart.“ Helene erwidert: „Meine neuen Schuhe haben ursprünglich
60 € gekostet und ich habe nur noch 33 € für sie bezahlt, also wurden meine Schuhe
noch stärker reduziert als deine.“
a) Wie viel Euro haben Antonias neue Schuhe vor dem Preisnachlass gekostet?
b) Um wie viel Prozent wurden Helenes neue Schuhe reduziert?
c) Wer von den beiden hat ein größeres „Schnäppchen“ gemacht?
3
Marc möchte 2700 € anlegen. Er hat zwei Angebote zur Auswahl (Bank A und B, siehe Randspalte).
a) Für welches Angebot sollte er sich entscheiden, wenn er das Geld genau ein Jahr anlegen möchte und wie viele Zinsen erhält er dann?
b) Welches Angebot ist lukrativer, wenn er sein Geld nur sieben Monate anlegen möchte?
c) Bei welcher Bank hat er nach fünf Jahren mehr Geld auf dem Konto und wie viel?
d) Wie viele Jahre müsste er sein Geld mindestens anlegen, damit sich die Anlage bei
Bank A lohnt?
e) Jonas erhält nach 5 Monaten bei Bank A 42 € Zinsen. Wie viel Geld hatte er angelegt?
4
Das Auto von Herrn Huber verbraucht
Verbrauch in ø
20
durchschnittlich 8 Liter Benzin auf 100 km.
15
Das Auto von Herrn Schreiber verbraucht
10
nur 7 Liter auf 100 km, das von Frau Krau5
Strecke in km
se 9 Liter auf 100 km. Der Graph und die
Tabelle stellen den durchschnittlichen Ben100
200
300
zinverbrauch eines dieser Autos dar.
Fig. 2
a) Zu welchem Auto passt die Tabelle in Fig. 1? Begründe.
b) Zu welchem Auto passt der Graph in Fig. 2? Begründe.
c) Gib für den Benzinverbrauch der drei Autos je eine Funktionsgleichung an, welche die
Anzahl der verbrauchten Liter y in Abhängigkeit von den gefahrenen Kilometern x angibt.
d) Julian bezweifelt, dass sich der Benzinverbrauch in Wirklichkeit exakt durch eine lineare Funktion beschreiben lässt. Nimm Stellung.
5
Nach dem Betriebspraktikum in Klasse 9 soll jeder Schüler einen Praktikumsbericht
von 7 Seiten abgeben. Auf jeder Seite sollen 50 Zeilen Text in der Schrift Arial und der
Schriftgröße 12 stehen. Ayse fällt nicht so viel ein, sodass sie unter diesen Bedingungen
nur auf 5 Seiten kommt. Sie überlegt sich, den Zeilenabstand zu ändern, sodass statt 50
Zeilen nur 38 Zeilen auf eine Seite passen.
a) Wie viele Seiten hat der Bericht von Ayse jetzt?
b) Wie viele Seiten hätte ein Bericht, der nach den obigen Vorgaben (sieben Seiten,
50 Zeilen pro Seite) geschrieben wurde, in Ayses Formatierung?
6
Aus den Lernstandserhebungen 2005
184
4500 m3 Bauschutt sollen abtransportiert werden. Fünf LKW würden dazu jeweils 60
Fahrten benötigen, wenn jeder LKW gleichmäßig beladen wird.
a) Wie viel m3 Bauschutt würde ein LKW dann pro Fahrt transportieren?
b) Von den fünf LKW fällt ein LKW aus. Er hat bis dahin bereits 20 Fahrten gemacht. Die
restlichen Fahrten dieses LKW müssen die übrigen LKW übernehmen. Wie viele Fahrten
muss dann jeder der übrigen LKW insgesamt machen?
c) Wie viele Fahrten müsste jeder LKW machen, wenn zum Abtransport der 4500 m3 nur
drei LKW zur Verfügung stehen würden?
d) Wie viele LKW würden benötigt, wenn jeder LKW genau 25 Fahrten machen soll?
VI Kompetenzen trainieren und vertiefen
7
Welcher der Graphen könnte zu welcher Zuordnung gehören? Begründe.
a)
b)
c)
d)
e)
f)
g)
(1)
(2)
(3)
(5)
(6)
(7)
(4)
Zeit ¥ zurückgelegter Weg bei konstanter Geschwindigkeit
Brenndauer ¥ Höhe einer brennenden Kerze
Volumen ¥ Füllhöhe einer bauchigen Vase (Fig. 1)
Zeit ¥ Geschwindigkeit beim Fahren einer Kurve
Zeit ¥ Abstand vom Boden zum Schaukelbrett.
Fig. 1
Alter eines Menschen ¥ seine Körpergröße
Überlege dir für den übrig gebliebenen Graphen eine passende Zuordnung. Begründe.
8
Alexander hat die Aufgabe, die Graphen der linearen Funktionen i) bis iii) zu zeichnen, macht hierbei aber einige Fehler. Finde die Fehler, indem du die Gleichungen zu den
von Alexander gezeichneten Geraden (Fig. 2 – 4) aufstellst und erläutere, wie diese Fehler
zustande gekommen sein könnten. Zeichne anschließend die richtigen Graphen.
i) y = 3 x + 2
ii) y = _32 x – 1
iii) y = – _41 x + _21
9
Lisa möchte ihren Handy-Tarif wechseln. Ihr stehen die zwei Angebote zur Verfügung:
Tarif 1:
Tarif 2:
0 € Grundgebühr pro Monat
7,49 € Grundgebühr pro Monat
17 ct/min in alle deutschen Netze
9 ct/min in alle deutschen Netze
a) Für welchen Tarif sollte sich Lisa entscheiden? Begründe rechnerisch und zeichnerisch.
b) Der Verkäufer versucht Lisa zu überreden, sich für eine Handy-Flatrate zu entscheiden.
Hierbei könnte sie für 24,99 € monatlich so viel telefonieren, wie sie möchte. Wie viele
Minuten müsste Lisa monatlich telefonieren, damit sich eine Flatrate für sie lohnt?
i)
11
Ein Schwimmbecken fasst 70 m3 Wasser. Es wird mit einem Schlauch gefüllt, durch
den in einer Stunde 1,9 m3 Wasser fließen. Nach 7 Stunden kommt ein zweiter Schlauch
hinzu, durch den in 2 Stunden 3,2 m3 Wasser fließen.
a) Zeichne den Graphen der Funktion Zeit ¥ Wasservolumen im Schwimmbecken.
b) Gib die Gleichungen für die Funktion Zeit ¥ Wasservolumen im Becken für den Zeitraum
bis zu sieben Stunden und für den Zeitraum von Beginn der 8ten Stunde an.
c) Nach wie vielen Stunden ist das Becken zur Hälfte, ganz bzw. zu 85 % gefüllt?
3
2
1
O
–3 – 2 –1
1 2 x
Fig. 2
ii)
y
3
2
1
O
–3 – 2 –1
1 2 x
Fig. 3
iii)
10
Manuela hat gelesen, dass die Brenndauer einer Kerze linear mit ihre Länge zusammenhängt. Sie zündet gleichzeitig zwei Kerzen an, misst nach einer bestimmten Zeit die
Längen und trägt sie in eine Tabelle ein (Fig. 5).
a) Hängt die Brenndauer einer Kerze nach Manuelas Messungen linear mit ihrer Länge
zusammen? Prüfe rechnerisch und zeichnerisch.
b) Gehe davon aus, dass der Zusammenhang tatsächlich exakt linear ist und je die ersten
beiden Messwerte von Manuela diesen Zusammenhang für Kerze 1 und 2 eindeutig beschreiben. Zu welchem Zeitpunkt sind beide Kerzen gleich lang?
y
y
3
2
1
O
–3 – 2 –1
1 2 x
Fig. 4
Zeit
Länge
1
Länge
2
2h
8 cm
7 cm
2,5 h
5 cm
6,1 cm
3h
24 min
0 cm
4,9 cm
VI Kompetenzen trainieren und vertiefen
Fig. 5
185
3 Geometrie
In der Geometrie geht es um Figuren in der Ebene und Körper im Raum. Sowohl
das Zeichnen von bestimmten Figuren und Körpern als auch das Berechnen von unbekannten Seiten, Winkeln, Umfängen, Flächen und Volumina sind wesentliche Bestandteile.
Winkel an Geraden
Dreiecke konstruieren
(Kongruenzsätze)
Besondere Linien im
Dreieck
Satz des Thales
C
C
A
C
B
Flächeninhalte von
Drei- und Vierecken
Scheitelwinkel sind gleich groß.
Nebenwinkel ergänzen sich zu 180°.
An Parallelen gilt:
Stufenwinkel sind gleich groß.
Wechselwinkel sind gleich groß.
Scheitelwinkel
a
a’
Stufenwinkel
Ein Dreieck lässt sich eindeutig konstruieren, wenn die folgenden Größen gegeben
sind:
– die drei Seiten (sss).
– eine Seite und die beiden anliegenden
Winkel (wsw).
– zwei Seiten und der von den Seiten eingeschlossene Winkel (sws).
– zwei Seiten und der Winkel, der gegenüber von der größeren Seite liegt (Ssw).
Alle Punkte auf der Mittelsenkrechten zu
A und B haben zu A und B den gleichen
Abstand. Die drei Mittelsenkrechten eines
Dreiecks schneiden sich im Umkreismittelpunkt (Fig. 1).
Alle Punkte auf einer Winkelhalbierenden
haben zu den beiden Schenkeln des Winkels den gleichen Abstand. Die drei Winkelhalbierenden eines Dreiecks schneiden
sich im Inkreismittelpunkt (Fig. 2).
a
Wechselwinkel
a’
g
a
sss
wsw
sws
Ssw
h
C
r
mb
C
a
B
mc
c
Fig. 2
c
r
r
A
ma
M
b
wb
Fig. 1
wa
W
r
a
b
wc
A
B
__
__
Liegt der Punkt C des Dreiecks ABC auf dem Halbkreis über der Strecke AB (Strecke AB
ist Durchmesser des Kreises), so ist c ein rechter Winkel. Umgekehrt gilt: Hat ein Dreieck
__
einen rechten Winkel bei C, dann liegt C auf dem Halbkreis über der Strecke AB.
Für Dreiecke mit der Grundseite a und der
zugehörigen Höhe ha gilt: A = _21 · a · ha.
A
c
a
D
d
c
D
A
VI Kompetenzen trainieren und vertiefen
b
a
C
C
h
A
d
b
ha
B
Für Parallelogramme bzw. Rauten mit der
Grundseite a und der zugehörigen Höhe h
gilt: A = a · h.
Für Trapeze mit a || c und der zu a gehörigen Höhe ha gilt: A = _21 · (a + c) · ha.
186
a’
h
a
g
b
Nebenwinkel
d
A
B
c
D c
C
h
b
B
a
C
b
ha
a
B
Für Kreise mit Radius r gilt:
Flächeninhalt: A = π · r2
Umfang: U = 2 · π · r
Für die Kreiszahl π gilt: π ≈ 3,14
Kreise
M
r
Für Quader mit den Seiten a, b und c gilt:
V = a·b·c
O = 2ab + 2bc + 2ac
c
a
Für Prismen mit der Grundfläche G, der
Höhe h und der Mantelfläche M gilt:
V = G · h.
O = 2 G + M.
Quader
Es sei:
Volumen: V
Oberfläche: O
Mantelfläche: M
b
Prismen
h
h
G
Für Zylinder mit dem Radius r und der
Höhe h gilt:
V = π · r2 · h
M = 2·π·r·h
O = M + 2 G = 2 · π · r · h + 2 · π · r2
G
Zylinder
r
r
h
h
M
r
Aufgaben
1
Bestimme jeweils die fehlenden Winkel. Begründe ausführlich.
b)
c)
a)
c
60°
40°
a b
a
50°
c
b
d)
c
b 60°
30°
40°
a
b
a
28°
55°
2
1 : 2000 bedeutet, dass
1 cm in der Zeichnung
2000 cm = 20 m in der
Wirklichkeit entspricht.
C
60
m
In einem Dreieck mit den Innenwinkeln a, b und c ist b um 20° größer als a
und c dreimal so groß wie a. Berechne die
Winkel.
B
120°
25°
A
Fig. 2
__
M ist die Mitte der Strecke AB. Die
__
Strecke MC ist halb so lang wie die Strecke
__
AB. Bestimme die fehlenden Winkel.
50°
Fig. 1
3
4
30°
80 m
1,5 m
a) Wie groß ist der Höhenunterschied
zwischen der Ebene und dem Berggipfel in
Fig. 1? Zeichne im Maßstab 1 : 2000.
b) Um die Breite eines Flusses zu bestimmen, kann man von einem Punkt A aus,
die Punkte B und C anpeilen. Die Peilung
hat nebenstehende Werte ergeben (Fig. 2).
Ermittle die Flussbreite mithilfe einer Konstruktion.
C
68,5°
A
M
B
VI Kompetenzen trainieren und vertiefen
187
5
Aus den Lernstandserhebungen 2004
In einem Koordinatensystem (1 cm entspricht 2 km) sind die Orte Esenshamm E (6 | 13)
und Schwanewede S (11 | 1) angegeben. Durch die Punkte P (9 | 15) und Q (7 | 1) verläuft der
Fluss Weser nahezu geradlinig.
a) Übertrage den Sachverhalt in ein Koordinatensystem.
b) Wie groß ist die Entfernung der beiden Orte voneinander?
c) Zwischen Esenshamm und Schwanewede soll ein Kraftwerk gebaut werden.
Dieses soll einen gleichen, aber möglichst geringen Abstand zu Esenshamm und Schwanewede haben. Gleichzeitig ist aufgrund der Hochwassergefahr ein Sicherheitsabstand
von 6 km zur Weser einzuhalten. Bestimme in der Zeichnung die Stelle, an der das Kraftwerk gebaut werden soll.
d) Trage den Ort Maltenkirchen M (1 | 9) ebenfalls ins Koordinatensystem ein. Konstruiere
den Standort des Kraftwerks, sodass dieses von allen drei Orten gleich weit entfernt ist.
Wie groß ist dann die Entfernung des Kraftwerks zum Fluss?
6
Entscheide, ob die folgenden Aussagen wahr oder falsch sind. Begründe.
a) In einem gleichseitigen Dreieck ist der Innkreismittelpunkt zugleich der Umkreismittelpunkt.
b) Es gibt kein Dreieck mit den Seitenlängen a = 3 cm, b = 5 cm und c = 9 cm.
c) Jedes gleichschenklige Dreieck mit einem 60°-Winkel ist gleichseitig.
d) Ein Dreieck mit genau einer Symmetrieachse ist gleichschenklig.
e) Drei Punkte, die nicht auf einer Geraden liegen, liegen immer auf einem Kreis.
7
a) Was soll in Fig. 1 zum Ausdruck gebracht werden? Nenne alle Beziehungen,
die sich aus Fig. 1 ablesen lassen.
b) Welches Viereck könnte gemeint sein?
Manchmal gibt es mehrere Möglichkeiten.
(I) Das Viereck hat vier rechte Winkel und
je zwei zueinander parallele Seiten.
(II) Die Diagonalen sind gleich lang.
(III) Alle vier Seiten sind gleich lang.
Quadrat
Rechteck
Raute
gleichsch.
Trapez
Drachen
Parallelogramm
Trapez
Viereck
Fig. 1
8
Fig. 2
8,7
1
Fig. 3
4,2
3,5
,2
25
Fig. 6
a) Ein Kästchen soll einem halben
Zentimeter entsprechen. Haben die beiden
Figuren (Fig. 2 und Fig. 3) gleiche Flächeninhalte? Begründe. Berechne außerdem die
Flächeninhalte der beiden Figuren.
b) Bestimme die Flächeninhalte von Fig. 4
und Fig. 5. Erläutere dein Vorgehen.
c) Jana behauptet: „Der Flächeninhalt des
Kreises kann nicht doppelt so groß sein,
wie der des Quadrates.“ Begründe mithilfe
von Fig. 6, ohne die Formel für den Flächeninhalt des Kreises zu verwenden.
23,6
15,1
2,7
1,4
30,2
Fig. 4
Fig. 5
9
a) Erkläre den Begriff Prisma, ohne
das Wort Prisma zu nennen.
b) Zeichne Fig. 7 in dein Heft und vervollständige zum Netz eines Prismas.
c) Bestimme das Volumen des Prismas.
188
VI Kompetenzen trainieren und vertiefen
Fig. 7
Berechne das Gesamtvolumen der Möbelstücke in Fig. 2 und Fig. 3.
m
0,
8
2,0 m
0,8 m
11
Fig. 2
2,4 m
6
m
1,2 m
0,8 m
0,
Ein DIN-A4-Blatt (21 cm breit und
29,7 cm lang) wird an den kurzen Seiten
zusammengeklebt, sodass eine Rolle entsteht (Fig. 1). Der Kleberand beträgt 7 mm.
a) Bestimme den Umfang der Papierrolle.
b) Erläutere, wie man aus den gegebenen
Größen den Radius des Zylinders bestimFig. 1
men kann und zeige rechnerisch, dass
r ≈ 4,62 cm beträgt.
c) Bestimme rechnerisch das Volumen des so entstandenen Zylinders und prüfe, ob es
größer als ein Liter ist.
d) Man kann das DIN-A4-Blatt auch andersherum zusammenrollen. Berechne das Volumen, wenn man auch hier 7 mm für den Kleberand benötigt. Um wie viel Prozent weicht
das Ergebnis von dem in c) ab.
e) Handwerker benutzen zur Kreisumfangberechnung oft die folgende Faustformel:
„Kreisumfang gleich Durchmesser mal 3 plus 5 Prozent vom Ergebnis“
e1) Berechne den Umfang der obigen Papierrolle (r ≈ 4,62 cm) mithilfe der Faustformel.
e2) Berechne den Näherungswert für π, der bei dieser Faustformel verwendet wird.
m
f) Welche Bruchzahl _
n mit n * {1; 2; 3, 4; 5; 7; 8; 9} hat die geringste Differenz zu π. Begründe deine Entscheidung.
1,2 m
0,
2
m
10
Fig. 3
12
Die Pizzeria „Bella Italia“ bietet Pizzen in zwei verschiedenen Größen und mit unterschiedlichen Belägen an. Eine große Pizza Margherita (mit Tomaten und Käse) mit einem
Durchmesser von 30 cm kostet 6,00 €.
a) Wie groß ist die Fläche der großen Pizza Margherita und wie lang ist ihr Rand?
b) Die Fläche der großen Pizza ist doppelt so groß wie die Fläche der kleinen Pizza. Wie
groß ist der Durchmesser der kleinen Pizza?
c) Wenn man bei der großen Pizza neben den Belägen Käse und Tomaten zusätzlich Salami und Champignons bestellt, so ist der Preis der Pizza um 16 % höher. Was kostet diese
Pizza (gerundet auf eine Nachkommastelle)?
d) Jede große Pizza Margherita hat außen herum eine 1,5 cm breite Randfläche, die nicht
belegt ist. Wie groß ist die belegte Fläche und wie groß die nicht belegte Fläche der großen Pizza? Wie viel Prozent der Gesamtfläche ist belegt?
e) Die Pizzeria „Bella Italia“ bietet auch ein Sonderangebot für Familien an und zwar eine
Familienpizza mit 45 cm Durchmesser, die 12,00 € kostet. Bewerte dieses „Sonderangebot“.
13
Die Quadratfolge in Fig. 4 ist nach einem bestimmten Muster aufgebaut.
a) Beschreibe die Regel zur Bildung der
Quadratfolge mit eigenen Worten.
b) Bestimme den Flächeninhalt der Quadrate durch Zerlegung. (Kästchenlänge
1 cm)
c) Welche allgemeine Regel zur Bestimmung der Flächeninhalte der Quadrate
lässt sich finden?
Fig. 4
VI Kompetenzen trainieren und vertiefen
189
4 Stochastik
Stochastik umfasst drei Teilgebiete. In der beschreibenden Statistik sammelt man
Daten, bestimmt relative Häufigkeitsverteilungen, stellt sie grafisch dar und beschreibt sie
durch Kenngrößen. In der Wahrscheinlichkeitsrechnung geht es um „theoretische“ Wahrscheinlichkeiten, mit denen man „reale“ relative Häufigkeiten bei Zufallsexperimenten und
statistischen Erhebungen vorhersagen möchte. In der beurteilenden Statistik, prüft man,
ob „angenommene“ Wahrscheinlichkeiten zu relativen Häufigkeiten passen.
Wahrscheinlichkeit
(Laplace und nicht
Laplace)
Den Ergebnissen von Zufallsexperimenten oder statistischen Erhebungen kann man
Wahrscheinlichkeiten zuordnen, die zusammen 100 % ergeben müssen. Die Wahrscheinlichkeiten geben an, welche relative Häufigkeit man auf lange Sicht erwartet. Wahrscheinlichkeiten sind gut gewählt, wenn sie relative Häufigkeiten gut vorhersagen.
Wenn bei einem Zufallsexperiment mit n möglichen Ergebnissen alle n Ergebnisse gleich
wahrscheinlich sind, spricht man von einem Laplace-Experiment und berechnet die Wahrscheinlichkeit p eines Ergebnisses mit der Formel p = _n1 .
Fig. 1
Gegenüberliegende Zahlen eines Quaders
ergeben in der Summe 7
und besitzen die gleiche
Wahrscheinlichkeit.
Summenregel
Beispiel
Bei einem Laplace-Würfel ist die Wahrscheinlichkeit für jede Augenzahl p = _61 ≈ 0,167 =
16,7 %.
Das Würfeln mit Quadern (Fig. 1) ist kein Laplace-Experiment, hier muss man die Wahrscheinlichkeiten aus relativen Häufigkeiten schätzen, wobei man auf Symmetrien achtet.
Aus relativen Häufigkeiten ergibt sich für die geschätzten Wahrscheinlichkeiten:
p (1) = p (6) = 0,1
p (2) = p (5) = 0,07
p (3) = p (4) = 0,33.
Man kann mehrere Ergebnisse zu einem Ereignis zusammenfassen. Die zugehörige Wahrscheinlichkeit erhält man, indem man die Wahrscheinlichkeiten der Ergebnisse addiert.
Beispiel
Die Wahrscheinlichkeit p für das Würfeln einer Zahl, die größer als 2 ist, beträgt
mit einem Laplace-Würfel p = _46 ≈ 0,667 = 66,7 %, da 3, 4, 5 und 6 größer sind als 2.
Baumdiagramm
Mehrstufige Zufallsexperimente beschreibt man durch Baumdiagramme. Das Baumdiagramm unten verdeutlicht die Berechnung der Wahrscheinlichkeit für das Ereignis „Augensumme 8“ beim zweimaligen Würfeln mit einem Laplace-Würfel.
Pfadregel
Die Wahrscheinlichkeit eines jeden Pfades erhält man, indem man die Wahrscheinlichkeiten längs des Pfades multipliziert.
1
6
—
1
6
—
1
1
6
—
1 2 3 4 5 6
1
6
—
2
1
6
1
6
—
1 2 3 4 5 6
1
6
1
6
—
—
1
6
—
3
—
1
6
—
1 2 3 4 5 6
1
6
—
4
1
6
1
6
—
—
1
6
—
1 2 3 4 5 6
Augensumme 8
1
6
—
5
1
6
—
1 2 3 4 5 6
1
6
—
6
1
6
—
1 2 3 4 5 6
Fig. 2
Beispiel
1
In Fig. 2 ist die Wahrscheinlichkeit für jeden Pfad p = _61 · _61 = _
.
Da
fünf
Pfade,
(2;
6);
36
(3; 5); (4; 4); (5; 3) und (6; 2), zur „Augensumme 8“ führen, ist die Wahrscheinlichkeit für
5
1
_
dieses Ereignis nach der Summenregel p = 5 · _
36 = 36 ≈ 0,139 = 13,9 %.
190
VI Kompetenzen trainieren und vertiefen
Bemerkung: Für den Quader in Fig. 1 ist die Wahrscheinlichkeit für „Augensumme 8“
p = 0,07 · 0,1 + 0,33 · 0,07 + 0,33 · 0,33 + 0,07 · 0,33 + 0,1 · 0,07 = 0,1691 = 16,91 %
Die Anzahl, mit der bei einer statistischen Erhebung (oder einem Zufallsversuch) Ergebnisse auftreten, heißt absolute Häufigkeit. Den zugehörigen Anteil an der Gesamtzahl nennt
man relative Häufigkeit. Es gilt: relative Häufigkeit =
absolute Häufigkeit
Gesamtzahl
__.
Beschreibende
Statistik
Häufigkeiten
Beispiel
Bei einem Test erzielten 30 Schüler die folgenden Punkte:
2; 3; 5; 5; 4; 7; 6; 8; 3; 6; 6; 2; 7; 2; 5; 5; 5; 3; 6; 3; 4; 5; 5; 7; 1; 2; 4, 5; 7; 9.
Durch Auszählen erhält man die absoluten und die relativen Häufigkeiten der verschiedenen Punkte (Fig. 1).
Punkte im Test
1
2
3
4
5
6
7
8
9
absolute H.
1
4
4
3
8
4
4
1
1
relative H.
3,3 %
13,3 %
13,3 %
10,0 %
26,7 %
13,3 %
13,3 %
3,3 %
3,3 %
Fig. 1
Die Kenngrößen bestimmt man wie folgt:
arithmetisches Mittel: (1 · 1 + 4 · 2 + 4 · 3 + 3 · 4 + 8 · 5 + 4 · 6 + 4 · 7 + 1 · 8 + 1 · 9) : 30 ≈ 4,73
Median (Zentralwert): Um den Median ablesen zu können, muss man die Liste sortieren:
122223333445555 555566667777789
Minium
unteres Quartil
Median = (5 + 5) : 2
oberes Quartil
Kenngrößen
Mittelwerte
Streuungsmaße
Maximum
Da die Länge der Liste (30) gerade ist, nimmt man als Median den Mittelwert des 15ten
und des 16ten Wertes. Man erhält als Median 5.
Spannweite: Maximum – Minumum = 9 – 1 = 8
Streuungsmaße
Quartilabstand: oberes Quartil – unteres Quartil = 6 – 3 = 3
/
Die Daten werden wie folgt in Diagrammen veranschaulicht:
3,3 %
3,3 %
13,3 %
13,3 %
26,7 %
10 %
13,3 %
13,3 %
3,3 %
12 %
16 %
20 %
oberes Quartil
Median
Arith. Mittel
unteres Quartil
Minimum
7
13 %
6
13 %
2
14 %
3
13 %
4
10 %
5
28 %
24 % 28 %
Boxplot
Kreisdiagramm
Aufgaben
10
Bestimme bei dem Glücksrad in Fig. 2 die Wahrscheinlichkeiten für die Ereignisse.
a) „Rot“
b) „7“
c) „ungerade Zahl“
d) „Teiler von 10“
e) „Die Summe der gedrehten Zahlen beim zweimaligen Drehen ist 6“
f) „Das Produkt der gedrehten Zahlen beim zweimaligen Drehen ist durch 3 teilbar“
1 2
3 4
1
Diagramme
1
9
3% 3%
8
3%
8 9
0
4%
8%
Balkendiagramm
Maximum
5 6 7
9
8
7
6
5
4
3
2
1
0
9
8
7
6
5
4
3
2
1
0
VI Kompetenzen trainieren und vertiefen
Fig. 2
191
2
Quader mit quadratischer Grundfläche
In einer Urne befinden sich eine gelbe, drei rote, zwei blaue und vier grüne Kugeln.
4
Die Wahrscheinlichkeit für „grün“ ist damit _
10 = 40 %. Wie ändert sich die Wahrscheinlichkeit für das Ziehen einer grünen Kugel wenn man
a) von jeder Farbe eine Kugel dazulegt,
b) von jeder Farbe eine Kugel wegnimmt,
c) zwei grüne und drei gelbe dazulegt,
d) eine grüne und alle blauen wegnimmt,
e) jeweils die Anzahl der Kugeln verdoppelt?
3
Die Summe gegenüberliegender Zahlen ist bei Quadern und Würfeln stets 7.
a) Ist die Wahrscheinlichkeit für „6“ beim Quader oder beim Würfel größer? Begründe.
b) Beim Quader ist die Wahrscheinlichkeit für eine „4“ 10 %. Wie groß müssen dann die
Wahrscheinlichkeiten für die übrigen Zahlen sein? Welche Annahmen machst du bei deiner Rechnung?
c) Bestimme für den Quader und den Würfel die Wahrscheinlichkeiten für das Ereignis „In
zwei Würfen ist die Augensumme größer als 6“ mithilfe eines Baumdiagramms.
d) Bestimme die Wahrscheinlichkeit des Ereignisses „In drei Würfen keine 1“.
Würfel
4
W‘ keiten
1
10%
2
10%
3
40%
4
20%
5
10%
6
10%
Fig. 1
Fig. 2
In der 8a haben die Schüler nach vielen Versuchen die Wahrscheinlichkeiten eines
Lego-Vierers wie in Fig. 1 geschätzt.
a) Erläutere, wie die 8a dabei vorgegangen sein könnte.
b) Berechne mit der Schätzung der 8a die Wahrscheinlichkeit dafür, dass man beim viermaligen Würfeln mit dem Lego-Vierer „mindestens zweimal die 4 (Noppen oben)“ erhält.
c) Inga steckt zwei der Lego-Vierer zu einem Doppelvierer zusammen (vgl. Fig. 2). Beschreibe, wie sich dadurch die Wahrscheinlichkeiten ändern. Gib eine Schätzung an.
d) Überprüfe die Schätzung durch eine Versuchsreihe mit 100 Würfen eines Doppelvierers.
5
Auf einem Fest hast du die Möglichkeit, zwischen zwei Lottovarianten zu wählen: „3
aus 5“ und „5 aus 7“. Du erhältst nur dann einen Preis, wenn du alle Zahlen richtig hast.
a) Schätze die Gewinnwahrscheinlichkeiten der beiden Lottovarianten.
b) Simuliere die beiden Lottovarianten zusammen mit deinem Nachbarn jeweils 50-mal
mit einem Würfel bzw. einem Kartenspiel. Berechne die relativen Häufigkeiten für „Spiel
gewonnen“ bzw. „Spiel verloren“.
c) Berechne die Wahrscheinlichkeiten für das Ereignis „Spiel gewonnen“ für beide Lottovarianten mithilfe eines Baumdiagramms. Für welche sollte man sich entscheiden und
inwiefern bestätigt die Simulation in b) die theoretisch ermittelten Wahrscheinlichkeiten?
d) Die Variante „3 aus 5“ kostet einen Euro Einsatz. Hat man drei Zahlen richtig, gewinnt
man 5 €, hat man nur zwei von drei Zahlen richtig, erhält man 2 € und bei einer richtigen
Zahl erhält man seinen Einsatz zurück. Berechne mithilfe der Simulation aus b) die relativen Häufigkeiten für 0, 1, 2, und 3 Treffer und anschließend die Wahrscheinlichkeiten.
Muss man bei dieser Spielvariante auf lange Sicht mit Einnahmen oder Verlusten rechnen?
6
Die Schüler der 8d wurden befragt, wie viele Stunden sie täglich „im Netz“ verbringen. Die Antworten werden im Folgenden aufgelistet (alle Angaben in h):
3; 2; 0; 1; 5; 1; 1; 3; 4; 2; 3; 2; 3; 7; 4; 1; 5; 4; 6; 2; 2; 3; 4; 2; 5; 3; 3; 5, 4
a) Bestimme das Minimum, das Maximum, die Spannweite, das arithmetische Mittel, den
Median und den Quartilabstand der aufgeführten Daten.
b) Bestimme die absoluten und relativen Häufigkeiten der auftretenden Zeiten und veranschauliche die Ergebnisse der Befragung in einem Säulendiagramm sowie einem Boxplot.
c) In der 8c verbringen die Schüler im Durchschnitt vier Stunden am Tag „im Netz“. Gib zu
diesem Durchschnittswert mindestens zwei mögliche Datenreihen mit jeweils 21 Daten
an.
192
VI Kompetenzen trainieren und vertiefen
7
Die 24 Schüler der Klasse 8 a machten die folgenden Angaben zu ihrer Lieblingssportart: Sieben Schüler nannten Fußball, ein Drittel nannte Volleyball und 25 % Badminton.
Alle anderen Schüler wählten Basketball. Jeder Schüler durfte nur eine Sportart angeben.
a) Stelle das Wahlverhalten der Schüler in einem Kreisdiagramm dar.
b) Jana möchte den Mittelwert aller Daten berechnen, kann sich aber nicht erinnern, wie
das geht. Kannst du ihr helfen?
8
In einer Umfrage wurden Erwachsene nach ihren monatlichen Ausgaben fürs Handy
gefragt. Die Umfrageergebnisse in Euro sind in einem Boxplot dargestellt (Fig. 1). Entscheide, ob die folgenden Aussagen wahr oder falsch sind. Begründe und korrigiere gegebenenfalls.
a) 50 % aller Frauen geben zwischen 65 und 140 € aus.
b) Der sparsamste Mann gibt weniger als 5 € aus.
c) 25 % der Frauen geben zwischen 45 und 65 € aus.
d) Mehr als 50 % der Frauen geben mehr als 80 € aus.
e) Weniger als 50 % der Männer geben mehr als 40 € aus.
f) Von den Männern geben mehr als 25 % zwischen 35 und 60 € aus.
140
120
100
80
60
40
20
0
Euro
Männer Frauen
Fig. 1
9
In der Tabelle in Fig. 3 ist das Ergebnis einer Umfrage zum Thema E-Mail-Versand aufgeführt. Befragt wurden Erwachsene im Alter von 25 bis 65 Jahren. Zu den Umfrageergebnissen wurde ein Zeitungsartikel (Fig. 2) verfasst.
a) Der Artikel enthält fünf Behauptungen. Welche davon kannst du aufgrund der Daten
bestätigen, welche nicht? Begründe durch geeignete Rechnung.
b) Stelle die Daten der Tabelle in Fig. 3 in einem Boxplot dar.
E-Mail, die schnelle Post
Das Versenden von E-Mails wird immer beliebter. Vor allem junge Menschen nutzen
diese Möglichkeit intensiv. Immerhin versenden über die Hälfte von ihnen regelmäßig
mehr als 4 E-Mails pro Tag, unter den über
30-Jährigen sind dies nur 30 %.
Auch scheint sich die Gruppe der unter
30-Jährigen über die Vorteile der elektronischen Post einig zu sein, senden doch mehr
als 50 % von ihnen zwischen 4 und 8 E-Mails
pro Tag, während in der älteren Gruppe die
Spanne von 0 bis 12 E-Mails pro Tag reicht.
Fig. 2
10
Anzahl der versandten
E-Mails pro Tag
0
1
2
3
4
5
6
7
8
9
10
11
12
Anzahl der Personen
bis 30 Jahre über 30 Jahre
3
29
5
21
17
16
25
13
17
6
30
11
13
9
6
2
10
3
4
0
5
7
2
0
1
2
Fig. 3
In einer Autobahnbaustelle darf höchstens Tempo 60 gefahren werden. Die Polizei
führt Geschwindigkeitskontrollen durch. Nach 15 Messungen kann man Folgendes sagen:
„Der Median der gemessenen Geschwindigkeiten beträgt 63 km/h. Von den 15 Messwerten sind hier 14 aufgelistet (alle Angaben in km/h): 55; 58; 59; 59; 60; 61; 62; 63; 64;
65; 65; 78; 97; 140.
a) Gib zwei mögliche Beispiele für die fehlende Geschwindigkeit an. Begründe.
b) Das arithmetische Mittel aller gemessenen Geschwindigkeiten beträgt 70 km/h. Berechne den noch fehlenden Geschwindigkeitswert.
c) Woran liegt es, dass in diesem Beispiel das arithmetische Mittel viel größer ist als der
Median? Wie könnte man das arithmetische Mittel vergrößern oder verkleinern, ohne den
Median zu verändern?
Aus den Lernstandserhebungen 2007
VI Kompetenzen trainieren und vertiefen
193
5 Kommunizieren und Argumentieren
Beim Kommunizieren und Argumentieren geht es darum, mathematische Informationen aus Texten, Tabellen und Graphen entnehmen und nutzen zu können. Der Umgang
mit mathematischen Begriffen und das Beweisen und Widerlegen von Behauptungen
spielen eine wesentliche Rolle.
Informationen entnehmen, deuten und
vorteilhaft nutzen
Nicht offensichtliche
Informationen aus den
Graphen lesen!
Welche Informationen
liefert ein Diagramm
nicht?
Einen Fehler finden
und seine Ursache präzise in Worte fassen
Fehler ggf. durch Nachrechnen identifizieren!
Ursachen des Fehlers
erkennen und verletzte
Rechenregeln in eigenen Worten erläutern!
194
Beispiel 1
Entfernung von zu Hause
Fig. 1 zeigt die Schulwege von Nadine und
Schule
Bianca. Beantworte, falls möglich, und begründe.
a) Wer geht früher von zu Hause los und
wie viele Minuten?
Nadine
b) Was macht Nadine zwischen 7.40 und
Bianca
Uhrzeit
7.45 Uhr?
c) Wer läuft ab 7.55 Uhr schneller?
7:30
7:40
7:50
8:00
Schulbeginn
d) Wie weit ist der Schulweg von Nadine?
Fig. 1
Mögliche Lösung:
a) Nadine geht 10 Minuten früher los als Bianca. Diese Information lässt sich direkt ablesen, da der Graph von Nadine um 7.30 Uhr beginnt und der von Bianca erst um 7.40 Uhr.
b) Nadine bleibt stehen. Zunächst einmal sucht man den Zeitpunkt 7.45 Uhr auf der x-Achse.
7.45 Uhr muss genau in der Mitte zwischen 7.40 Uhr und 7.50 Uhr liegen. Zwischen 7.40 und
7.45 Uhr besitzt der Graph von Nadine keine Steigung, also nähert sich Nadine in diesem
Zeitraum nicht der Schule; sie bleibt also stehen. Theoretisch wäre es auch möglich, dass sie
im Kreis um die Schule geht, was allerdings sehr unrealistisch ist.
c) Ab 7.55 Uhr läuft Bianca schneller als Nadine. 7.55 Uhr findet man wieder in der Mitte
zwischen 7.50 Uhr und 8.00 Uhr. Ab 7.55 Uhr wird der Graph von Bianca steiler. Ab diesem
Zeitpunkt legt sie also die gleiche Entfernung zur Schule in weniger Zeit (in fünf Minuten)
als Nadine (in zehn Minuten) zurück, sie ist also schneller als Nadine.
d) Diese Frage kann nicht eindeutig beantwortet werden, da auf der y-Achse keine Angabe zur Entfernung gemacht wurde. Hier kann aber mithilfe der Zeitangaben geschätzt
werden. Da Nadine ohne die „Pause“ (vgl. Textaufgabe b) 30 Minuten zur Schule geht und
ein Fußgänger etwa 4 km/h schnell ist, ist ihr Schulweg vielleicht etwa zwei Kilometer lang.
Beispiel 2
Die folgenden Termumformungen sind falsch. Wie könnten diese Fehler zustande gekommen sein? Welche Rechenregeln wurden dabei verletzt?
a) (3 s + 4 t)2 = 3 s2 + 24 s t + 4 t2
b) – 3 x (2 x – 5) = – 6 x2 – 15 x = – 21 x
Mögliche Lösung:
a) Hier wurde die erste binomische Formel (a + b)2 = a2 + 2 a b + b2 benutzt. Es wurde aber
außer Acht gelassen, dass dabei a = (3 s) und b = (4 t) gilt und deshalb nicht nur die Variablen s und t quadriert werden müssen. Man hätte also (3 s)2 = 9 s2 und (4 t)2 = 16 t2 rechnen müssen und erhielte dann insgesamt: (3 s + 4 t)2 = 9 s2 + 24 s t + 16 t2.
b) Zunächst einmal wurde die Klammer aufgelöst. Hierbei wurde nicht beachtet, dass sich
durch das negative Vorzeichen vor der Klammer beim Auflösen alle Vorzeichen in der Klammer „umdrehen“. Es müsste heißen: – 3 x (2 x – 5) = – 6 x2 + 15 x, da – 3 x · (–5) = + 15 x.
In der zweiten Umformung wurde nicht beachtet, dass sich beim Addieren oder Subtrahieren
von Termen nur gleichartige Terme zusammenfassen lassen. Der Term „– 6 x2 + 15 x“ lässt
sich also nicht weiter vereinfachen.
VI Kompetenzen trainieren und vertiefen
Beispiel 3
Entscheide, ob die folgenden Aussagen wahr oder falsch sind. Begründe.
a) Anna behauptet: „Ein Viereck, bei dem die gegenüberliegenden Seiten gleich lang und
parallel sind, ist immer ein Rechteck.“
b) Martin meint: „Multipliziert man eine Zahl mit sich selbst, erhält man immer eine Zahl,
welche größer ist als die ursprüngliche Zahl.“
c) Theodor behauptet: „Setzt man in den Term 21 n + 15 eine natürliche Zahl für n ein, so
erhält man immer eine Zahl, die durch 3 teilbar ist.“
Mögliche Lösung:
D
C
a) Es stimmt, dass bei jedem Rechteck die
gegenüberliegenden Seiten gleich lang
und parallel sind. Die Behauptung von
Anna ist aber trotzdem falsch, denn auch
in einem Parallelogramm (Fig. 1) sind die
A
B
gegenüberliegenden Seiten gleich lang
Fig. 1
und parallel.
b) Die Behauptung ist falsch, denn z. B. 0,5 · 0,5 = 0,25 < 0,5. Die Aussage ist für alle Zahlen richtig, die größer als 1 oder kleiner als 0 sind, also z. B. 1,5 oder auch – 0,5, denn
1,5 · 1,5 = 2,25 > 1,5 und (– 0,5) · (– 0,5) = 0,25 > – 0,5. Für die Zahlen 0 und 1 und alle Zahlen, die zwischen 0 und 1 liegen, ist die Behauptung falsch.
c) Die Behauptung ist wahr, denn 21 n und 15 sind durch 3 teilbar, also auch deren Summe. Es gilt: 21 n + 15 = 3 (7 n + 5) und ein Produkt aus 3 und einer anderen natürlichen
Zahl ist immer durch 3 teilbar.
Behauptungen
überprüfen
Gegenbeispiel finden,
welches alle genannten
Eigenschaften hat und
trotzdem kein Rechteck
ist!
Behauptung an unterschiedlichen Zahlenbeispielen überprüfen!
Beispiele sind hilfreich,
reichen aber nicht aus,
um die wahre Aussage
zu begründen.
Aufgaben
1
Nimm Stellung zu dem folgenden Zeitungsausschnitt:
„Jede dritte Ehe wird geschieden. In Großstädten sogar jede vierte.“
2
Die Achtklässler eines Gymnasiums wurden befragt, welche Haustiere sie haben.
Von den Befragten haben 50 % eine Katze, 20 % einen Hund, 17 % einen Vogel, 15 % einen
Hamster und 10 % ein Kaninchen. 18 % der Befragten besitzen kein Haustier.
a) Jens hat das Umfrageergebnis im Kreisdiagramm (Fig. 2) dargestellt. Katja behauptet,
dass etwas mit dem Kreisdiagramm nicht stimmen kann. Was meint Katja?
b) Wieso lässt sich zu den Umfrageergebnissen kein passendes Kreisdiagramm zeichnen
und wie kann es zu derartigen Umfrageergebnissen kommen?
c) Zeichne ein Diagramm, das zu den Umfrageergebnissen passt.
Aus den Lernstandserhebungen 2007.
Katze
keine
Hund
Vogel
Kaninchen
Hamster
Fig. 2
3
Dies ist ein Auszug aus Leonards Klassenarbeit zum Thema Termumformungen. Welche Rechenregel hat Leonard verletzt und auf welche Weise? Erläutere und korrigiere die
Fehler.
a) (a – 3) (a + 5) = a2 – 15
b) 6 s3 – 2 s2 = 4 s
2
c) (4 + x)2 = 16 + x2
d) 2 5 x – y 3 3 = 5 x2 – 5 x y3 + y9
e) _
2 = x + 5 = 5x
g) – 3 x (5 – 2 x) = – 15 x – 2 x = – 17 x
____
f) 9x2 + 16 = x + 4
__
__
_
_
_
h) 2 948 + 7 927 = 6 93 + 10 93 = 16 93
i) 2 x · 3 x – 2 x = 2 x · x = 2 x2
j) √22 + √3 = √25 = 5
2x + 5
___
__
___
VI Kompetenzen trainieren und vertiefen
195
4
Tipp: Prüfe erst an Beispielen.
Lena behauptet, dass die Summe von sieben aufeinander folgenden Zahlen immer
durch sieben teilbar ist. Hat sie Recht? Begründe.
5
Aus den Lernstandserhebungen 2004.
Aus den Lernstandserhebungen 2007.
Die Abbildung zeigt die Schulwege von
Entfernung von der Schule
Paula, Maria und Peter. Alle drei besuchen
die gleiche Schule, wohnen aber unterPaula
schiedlich weit weg von ihr. Entscheide, ob
Peter
die folgenden Aussagen stimmen können
oder nicht oder ob sie sich nicht beantworMaria
ten lassen. Begründe deine Entscheidung.
a) Paula wohnt am weitesten von der
Uhrzeit
Schule entfernt.
7:45
8:00
8:15
b) Peter geht am langsamsten und kommt
daher auch als letzter in der Schule an.
c) Paula holt Maria von zu Hause ab. Maria ist aber noch nicht fertig, als Paula kommt.
d) Peter hat etwas zu Hause vergessen, was ihm auf halbem Wege einfällt.
e) Paula geht mit Maria schneller als ohne Maria.
f) Maria wohnt 1 km von der Schule entfernt.
6
An jeder Ecke eines Würfels treffen drei Seitenflächen aufeinander.
a) Wie groß kann die Summe der Augenzahlen an einer Ecke eines Würfels höchstens
und wie groß muss sie mindestens sein? Begründe.
b) Kann die Summe der Augenzahlen an einer gemeinsamen Ecke acht sein? Begründe
deine Entscheidung.
7
Entscheide, ob die Aussagen wahr oder falsch sind. Begründe oder widerlege.
a) Jedes Quadrat ist ein Rechteck.
b) Die Graphen einer quadratischen und einer linearen Funktion schneiden sich entweder
gar nicht oder genau in zwei Punkten.
c) Jede ganze Zahl ist auch eine rationale Zahl.
d) Ein Bruch, bei welchem der Zähler ein Teiler vom Nenner ist, ist immer eine ganze Zahl.
e) Der Graph jeder linearen Funktion schneidet die x-Achse genau einmal.
f) Eine Raute mit vier rechten Winkeln ist ein Quadrat.
g) Die Wahrscheinlichkeit, eine Zahl zu würfeln, die größer ist als drei, ist größer als die
Wahrscheinlichkeit dafür, eine Zahl zu würfeln, die kleiner oder gleich drei ist.
h) Von zwei Brüchen ist derjenige größer, der den kleineren Nenner hat.
i) Jede Raute ist auch ein Trapez.
8
Greta behauptet: „Setzt man eine natürliche Zahl n in den Term 8 n + 1 ein, so erhält
man immer eine ungerade Zahl.“
a) Entscheide, ob Greta Recht hat, und begründe deine Entscheidung.
b) Lässt sich mithilfe des Terms 8 n + 1 jede ungerade Zahl darstellen? Begründe.
c) Finde drei weitere Terme, mit denen man nur ungerade Zahlen darstellen kann, und
drei, mit welchen man nur gerade Zahlen darstellen kann.
d) Gibt es einen Term, mit welchem man jede ungerade bzw. gerade Zahl darstellen
kann? Begründe und gib diesen Term gegebenenfalls an.
9
Volker behauptet: „Wenn drei Dienstage in einem Monat auf ein geradzahliges Tagesdatum fallen, dann ist der 21. dieses Monats ein Sonntag.“
Hat Volker Recht? Begründe.
196
VI Kompetenzen trainieren und vertiefen
10
a) Im Folgenden wird ein besonderes Viereck konstruiert. Formuliere zu Schritt 1 bis 7
die passenden Konstruktionsschritte.
A
A
A
B
B
B
(2)
(1)
B
C
C
A
A
A
B
S
D
B
S
(6)
(5)
C
S
(3)
C
S
A
(4)
C
D
(7)
C
C
b) Wie nennt sich das Viereck aus a) und welche Eigenschaften dieses Vierecks werden
bei der Konstruktion ausgenutzt?
c) Gib eine eigene Definition für das Viereck aus a) an und überlege, für welche anderen
besonderen Vierecke diese Definition ebenfalls gilt. Begründe deine Überlegungen.
11
In die sechs Lücken sollen sechs Zahlen eingesetzt werden, sodass eine Rechenaufgabe mit Brüchen entsteht.
º º º
_ · _ : _ = ?
º º º
a) Setze die Zahlen 1, 2, 3, 6, 8 und 9 so in die Lücken der Bruchaufgabe ein, dass das Ergebnis möglichst groß ist, und berechne anschließend.
b) Setze die Zahlen 1, 2, 3, 6, 8 und 9 so in die Lücken ein, dass das Ergebnis möglichst
klein ist, und berechne anschließend.
c) Begründe deine Wahl in a) und b).
d) Wie würdest du beim Einsetzen von sechs beliebigen Zahlen vorgehen?
e) Wie würdest du vorgehen, wenn statt des positiven Vorzeichens ein negatives Vorzeichen vor dem Bruch stünde?
12
Bestimme die gekennzeichneten Winkel rechnerisch. Begründe ausführlich.
a)
b)
c)
110°
=
a
b
b
=
35°
46°
66°
a
b
a
c
28°
Tipps:
1. Es handelt sich nur
um Skizzen, ausmessen
kannst du also nicht!
2. Notiere zunächst alle
Winkelbeziehungen, die
du kennst.
13
Nicole und Meikel streiten sich darum, wer abwäscht. Meikel schlägt vor: „Wenn ich
deine Gedanken erraten kann, wäschst du ab, sonst wasche ich ab.“ Nicole willigt ein und
Meikel fordert sie auf: „Denke dir eine beliebige Zahl, verdopple sie und addiere anschließend 3, multipliziere dann das Ergebnis mit 5 und addiere anschließend 15. Dividiere
das Ergebnis durch 10 und subtrahiere die anfangs gedachte Zahl. Die Zahl, an die du
jetzt denkst, ist die 3.“ Nicole versucht, während sie abwäscht, Meikels Trick zu verstehen.
Kannst du ihr dabei helfen? Zeige, dass bei Meikels Trick immer 3 herauskommt.
VI Kompetenzen trainieren und vertiefen
197
6 Problemlösen
Man beschäftigt sich beim Problemlösen mit Problemen, deren Lösungsweg nicht
unmittelbar erkennbar ist. Oft muss man zunächst einmal die Aufgabe genau verstehen
und sich darüber klar werden, was gegeben und was gesucht ist. Hat man die Aufgabe
verstanden, denkt man sich einen Plan aus. Man kann z. B. das Problem in Teilprobleme
zerlegen oder man versucht, das Problem durch systematisches Probieren zu lösen. Auch
die Einführung von Variablen und das Aufstellen von Termen oder Gleichungen sind oft
sinnvoll. Ebenso können Skizzen oder Schätzungen bei der Lösung des Problems helfen.
Hat man mit einer Strategie einen Plan für das Vorgehen gefunden, führt man diesen
als nächstes aus. Man löst also z. B. die zuvor aufgestellte Gleichung. Nachdem man eine
Lösung gefunden hat, muss man in einer Rückschau überprüfen, ob diese Lösung vor dem
Hintergrund der Fragestellung sinnvoll und realistisch ist.
Ausprobieren
1
2
3
5
x
=
4
Fig. 1
Erst einmal ausprobieren und Vermutungen
anstellen!
Nach Regeln suchen!
Entdeckte Regeln systematisch anwenden!
Nach Strukturen
suchen
1. Jahr 2. Jahr 3. Jahr
Fig. 2
Muster sinnvoll
fortsetzen!
Tabelle anlegen!
198
Beispiel 1
Wie heißt die größte Zahl, die mit einmaligem Benutzen der in Fig. 1 abgebildeten Tasten
eines Taschenrechners erzeugt werden kann?
Mögliche Lösung:
Durch Ausprobieren erhält man z. B.
5432 · 1 = 5432
3421 · 5 = 17 105
4321 · 5 = 21 605
5321 · 4 = 21 284.
Wenn man eine vierstellige Zahl mit einer einstelligen multipliziert, ist das dritte der vier
Ergebnisse das größtmögliche. Kann das Ergebnis größer werden, wenn man eine zweistellige mit einer dreistelligen Zahl multipliziert? Auch hier probiert man zunächst aus.
321 · 54 = 17 334
421 · 53 = 22 313
531 · 42 = 22 302
521 · 43 = 22 403
Es kommt offensichtlich darauf an, an welcher Stelle die größten Ziffern stehen. Es
scheint klar, dass die 4 und die 5 an der ersten Stelle der beiden zwei- und dreistelligen
Zahlen stehen müssen und dass die 1 als kleinste Zahl an einer der letzten Stellen stehen
muss. Außerdem führt eine 3 an der Zehnerstelle der dreistelligen Zahl zu einem größeren Ergebnis als an der Einerstelle dieser Zahl.
Es gibt sechs Möglichkeiten, sodass die 4 und die 5 vorne stehen, die 1 eine Einerstelle
besetzt und die 3 innerhalb der dreistelligen Zahl die Zehnerstelle einnimmt:
531 · 42 = 22 302
532 · 41 = 21 812
521 · 43 = 22 403
431 · 52 = 22 412
432 · 51 = 22 032
421 · 53 = 22 313
Das größte Ergebnis erhält man also bei 431 · 52 = 22 412.
Beispiel 2
Beim Igelbaum (Fig. 2) wachsen jedes Jahr aus jeder Spitze zwei neue Spitzen. Wie viele
Spitzen hat der Igelbaum nach 8 Jahren?
Jahr
1 2 3 4 5
Mögliche Lösung:
Anzahl der
1 2 4 8 16
Man könnte zunächst die Idee haben, die
Spitzen
Zeichnung fortzuführen. Es ist sogar hilfreich, die Gestalt des Baumes im 4. Jahr zu
2·8 = 16, da ja aus jeder der
skizzieren (Fig. 3). Es wird aber schnell klar,
acht Spitzen zwei werden
dass es nicht sinnvoll ist, dies für die ver4. Jahr
bleibenden 4 Jahre zu Ende zu führen, da
Fig. 3
die Zeichnungen immer unübersichtlicher
werden. Was kann man noch tun, außer zu zeichnen? Man kann versuchen, eine geeignete Zahlenreihe zu erzeugen. Man könnte z. B. eine Tabelle anlegen, in der jedem Jahr die
Anzahl der Spitzen des Igelbaumes zugeordnet wird (vgl. Fig. 3).
VI Kompetenzen trainieren und vertiefen
Da sich die Anzahl der Spitzen jedes Jahr verdoppelt, lässt sich die Anzahl der Spitzen im
achten Jahr A (8) berechnen durch A (8) = 1 · 2 · 2 · 2 · 2 · 2 · 2 · 2 = 27 = 128, denn im ersten Jahr hat der Baum nur eine Spitze. Mit jedem Jahr kommt also einmal der Faktor „2“
hinzu, sodass sich auch die Spitzen z. B. im 17. Jahr einfach berechnen lassen:
A (17) = 1 · 2 · 2 · 2 · 2 · 2 · 2 · 2 · 2 · 2 · 2 · 2 · 2 · 2 · 2 · 2 · 2 = 216 = 65 536.
Beispiel 3
Marc und seine Mutter sind heute zusammen 65 Jahre alt. Vor 10 Jahren war die Mutter
4-mal so alt wie Marc. Wie alt sind Marc und seine Mutter heute?
Mögliche Lösung:
1. Schritt: Variablen einführen und Terme aufstellen
Da man das Alter von Marc und seiner Mutter nicht kennt, führt man zunächst geeignete
Variablen ein und bestimmt deren Bedeutung. Man benötigt das Alter von Marc und seiner Mutter heute und vor 10 Jahren:
x = Alter von Marc heute, also x – 10 = Alter von Marc vor 10 Jahren
y = Alter von Marcs Mutter heute, also y – 10 = Alter von Marcs Mutter vor 10 Jahren
2. Schritt: Gleichungen aufstellen
Da Marc und seine Mutter heute zusammen 65 Jahre alt sind, gilt: x + y = 65 (I)
Da Marcs Mutter vor 10 Jahren 4-mal so alt war wie Marc, gilt: 4 · (x – 10) = y – 10 (II)
(Marcs Alter vor 10 Jahren muss mal 4 genommen werden, um das Alter von Marcs Mutter vor 10 Jahren zu erhalten.).
3. Schritt: Gleichungen lösen
I:
x + y = 65
|–x
Man hat jetzt zwei Gleichungen und zwei
Ib:
y = 65 – x
Unbekannte, also ein lineares GleichungsJetzt wird Ib in II eingesetzt:
system, das sich lösen lässt.
4 · (x – 10) = (65 – x) – 10
4 x – 40 = 65 – x – 10
4 x – 40 = 55 – x
| + x + 40
5 x = 95
|: 5
x = 19  y = 46
Antwort: Marc ist heute 19 und seine Mutter 46 Jahre alt, denn 19 + 46 = 65 und 9 · 4 = 36.
Bildungsgesetz für das
Muster erkennen und
einen passenden Term
aufstellen!
Terme und Gleichungen nutzen
Variablen einführen, Terme aufstellen und ihre
Bedeutung notieren!
Beziehungen aus dem
Text in Terme und Gleichungen übersetzen!
Gleichungen noch einmal am Text überprüfen
und lösen!
Lösung immer noch
einmal am Text überprüfen!
Aufgaben
1
Wie lautet die größte Zahl, die mit einmaligem Benutzen der abgebildeten Tasten eines Taschenrechners berechnet werden kann?
2
3
5
6
8
9
x
=
2
a) Pia hat drei gleich aussehende Gewichte. Eines davon ist leichter als die anderen.
Wie kann sie das leichte Gewicht mit einmaligem Wiegen auf einer Balkenwaage finden?
b) Jetzt hat sie neun gleich aussehende Gewichte, von denen eines leichter ist als die
anderen. Wie viele Wiegevorgänge muss sie mindestens durchführen, um herauszufinden,
welches Gewicht leichter ist?
c) Wie viele Wiegevorgänge sind nötig, um herauszufinden, welches das leichtere Gewicht
von 27 gleich aussehenden Gewichten ist?
3
Wo im Würfel liegen die anderen gelben Dreiecke? Zeichne die Würfelnetze in
dein Heft und zeichne die fehlenden gelben Dreiecke ein.
VI Kompetenzen trainieren und vertiefen
199
4
Fig. 1 zeigt die ersten drei Muster einer Folge von Streichhölzern.
a) Wie viele Streichhölzer werden für das 43. Muster benötigt?
b) Gib einen allgemeinen Term für die Anzahl der Streichhölzer im n-ten Muster an.
b) Das wievielte Muster kann man mit 109 Hölzern legen?
1. Muster
2. Muster
3. Muster
Fig. 1
5
Wie lässt sich mithilfe eines 8-Liter-Gefäßes und eines 5-Liter-Gefäßes, die beide keinerlei Markierung besitzen, ein Liter abmessen? Hierzu darf man so viel Wasser einfüllen
und ausschütten, wie man möchte.
6
Hinweis: Zeichne das
Zifferblatt und die Kästchen in dein Heft.
a) Teile das Ziffernblatt einer Uhr mit
nur einer geraden Linie, sodass die Summe
der Zahlen in jeder Hälfte gleich ist.
b) Teile das Ziffernblatt mit zwei geraden
Linien, sodass die Summe der Zahlen in
den entstehenden Teilen gleich ist.
c) Verteile die Zahlen von 1 bis 8 so in die
Kästchen von Fig. 3, dass weder senkrecht
noch waagerecht noch diagonal Zahlen aneinander grenzen, die aufeinander folgen.
11
12
1
2
10
9
3
4
8
7
6
5
Fig. 2
Fig. 3
7
Von vier Zahlen ist die zweite um 7 größer als die erste, um 11 kleiner als die dritte
und halb so groß wie die vierte. Die Summe der vier Zahlen ist 114. Wie heißen die Zahlen?
8
Während der Fußball-WM 2006 in
Deutschland wurden riesige Skulpturen
von Fußballschuhen, die vor dem Bahnhof
in Berlin auf den deutschen Erfindergeist
aufmerksam machen sollten, zu einer Touristenattraktion.
a) Welche Schuhgröße haben diese Schuhe
ungefähr?
b) Wie groß wäre der Mensch ungefähr,
dem solche Schuhe passen würden?
9
Erinnerung: 33 = 3 · 3 · 3
200
Anton und Emi streiten sich darum, wer den Müll hinunterbringt. Anton schlägt vor:
„Du denkst dir eine Zahl von 1 bis 100. Dann gibst du diese Zahl in den Taschenrechner ein
und rechnest ‚hoch drei’. Dann sagst du mir das Ergebnis und ich sage dir ohne Taschenrechner sofort die anfangs gedachte Zahl.“ Emi willigt ein, denn das schafft Anton ihrer
Meinung nach nie. Sie gibt 573 in den Taschenrechner ein und sagt zu Anton: „185 193“.
Anton sagt sofort: „57!“ Emi ist verblüfft und trägt verwundert den Müll hinuter. Auf der
Treppe zum Hof grübelt und grübelt sie. Wie hat Anton das nur hinbekommen?
Finde heraus, wie Antons Trick funktioniert. Was musste er tatsächlich wissen und was ist
unwichtig?
VI Kompetenzen trainieren und vertiefen
10
Wie viele dreistellige Zahlen gibt es, deren 3 Ziffern untereinander und von 0 verschieden sind und bei denen das Produkt ihrer Ziffern eine durch 81 teilbare Zahl ist?
11
Fünf Kinder möchten gemeinsam wippen; sie wiegen 15 kg, 25 kg, 30 kg, 35 kg und
45 kg. Wie sollten sie sich am besten auf der Wippe in Fig. 1 verteilen? Bedenke: Wenn ein
Kind doppelt so viel wiegt wie ein anderes, sollte es nur halb so weit von der Mitte der
Wippe entfernt sitzen. Erkläre, wie du vorgegangen bist.
Fig. 1
12
Aus dem roten Quadrat wird ein anderes Quadrat so ausgeschnitten, dass ein 6 cm
breiter Rahmen entsteht (vgl. Fig. 2). Der Flächeninhalt des Rahmens beträgt 456 cm2. Wie
groß ist der Flächeninhalt des inneren Quadrats?
13
Von einer quadratischen Fläche soll an einer Stelle eine Fläche entnommen werden
(1.) und die gleiche Fläche soll an eine andere Stelle des Quadrats angesetzt werden (2.)
(Fig. 3). Durch dieses Verfahren ändert sich zwar der Umfang der Figur, nicht aber der Flächeninhalt.
a) Verändere irgendein Quadrat auf diese Weise so, dass sich sein ursprünglicher Umfang
verdoppelt, die Fläche aber nicht in Teilflächen zerstückelt wird. Du darfst das Verfahren
mehrfach anwenden.
b) Wie müsste man vorgehen, um den Umfang zu verdreifachen?
Fig. 2
2.
1.
Fig. 3
14
a) Kann man das „Haus vom Nikolaus“
(Fig. 4) in nur einem Zug zeichnen, ohne
den Stift abzusetzen und ohne eine Linie
doppelt zu zeichnen? Wenn ja, in welcher
oder welchen Ecken darf man beginnen
und wo endet man?
b) Kann man das „Haus vom WeihnachtsFig. 4
Fig. 5
Fig. 6
mann“ (Fig. 5), das direkt neben dem Haus
vom Nikolaus steht und dem deshalb eine
Hauswand fehlt, ebenfalls in einem Zug
zeichnen?
c) Lassen sich auch beide Häuser zusammen (Fig. 6) in einem Zug zeichnen?
d) Unter welchen Voraussetzungen lassen sich derartige Häuser in einem Zug zeichnen
und wann nicht?
15
Fig. 7 zeigt die ersten drei Muster einer Folge aus Punkten.
a) Wie viele Punkte benötigt man für das
13te Muster?
b) Welcher allgemeine Term lässt sich für
die Anzahl der Punkte im n-ten Muster angeben?
Pollys Tipp:
Zu 14 d): Zähle die Linienendpunkte in den
jeweiligen Ecken und
überlege dir, was die
Anzahl mit dem Gelingen der Aufgabe zu tun
haben könnte.
Fig. 7
16
Zwei junge Mathematiker lernen sich am Neujahrstag des Jahres 1997 auf einer Party
kennen. Der ältere von beiden fragt den jüngeren nach seinem Alter. Dieser stellt das folgende Rätsel: „Wenn du die Quersumme meines vierstelligen Geburtsjahres bildest, weißt
du, wie alt ich bin.“ Der ältere überlegt eine Weile und gratuliert der neuen Bekanntschaft
plötzlich zum Geburtstag. Wie alt war der jüngere Mathematiker und woher wusste der
ältere, dass er ausgerechnet heute Geburtstag hatte?
Erinnerung: Die Quersumme der Zahl 341 ist
3 + 4 + 1 = 8.
VI Kompetenzen trainieren und vertiefen
201
7 Modellieren
Beim Modellieren geht es darum, passende mathematische Modelle (Terme, Gleichungen, Funktionen, Figuren, Diagramme, Tabellen, Zufallsversuche) für Probleme aus
dem Alltag zu finden und diese Probleme mithilfe dieser Modelle zu lösen.
Bekannte Modelle auf
Tauglichkeit überprüfen!
Fehlende Informationen
beschaffen!
Funktionsgleichung aufstellen und Bedeutung
der Variablen festlegen!
Eigene Erfahrungen einbeziehen und Modellgrenzen festlegen!
Starnberg
Pöcking
Feldafing
Starnberger
See Münsing
Maßstab 1:500 000
Fig. 1
Nötige Genauigkeit gegen Aufwand der Vorgehensweise abwägen!
Ergebnisse mit „Literaturangaben“ vergleichen!
202
Beispiel 1 Funktionen als Modelle
Familie Meyfahrt fährt mit dem Auto von Köln nach Barcelona. Nach 100 km Fahrt sind 8
Liter Benzin verbraucht. Nach 200 km sind insgesamt 17 Liter verbraucht. Ein Liter Benzin
kostet etwa 1,32 €. Wie viel Geld muss Familie Meyfahrt für die einfache Fahrt einplanen?
Mögliche Lösung:
1. Übersetzen der Situation in ein mathematisches Modell:
Man kann davon ausgehen, dass der Benzinverbrauch näherungsweise proportional zu
den gefahrenen Kilometern ist. Eine lineare Funktion durch den Ursprung könnte also
ein geeignetes Modell zur Lösung der Aufgabe sein. Die Länge der Strecke von Köln nach
Barcelona muss zur Lösung der Aufgabe noch herausgefunden werden.
2. Mit dem Modell rechnen:
Da das Auto auf den ersten 100 Kilometern 8 Liter und auf den nächsten 100 Kilometern
9 Liter verbraucht hat, kann man von einem durchschnittlichen Verbrauch von 8,5 Litern
pro 100 km ausgehen. Also modelliert die Funktion f mit f (x) = 0,085 x den Benzinverbrauch des Autos der Familie Meyfahrt. x entspricht hierbei der Anzahl der gefahrenen
Kilometer und y = f (x) entspricht dem Benzinverbrauch in Litern.
Im Internet findet man für die Autostrecke von Köln nach Barcelona die Angabe 1350 km.
Also verbraucht das Auto insgesamt f (1350) = 0,085 · 1350 ≈ 114,75 Liter Benzin.
Die Familie muss etwa 114,75 · 1,32 € = 151,47 € ≈ 150 € Benzinkosten einplanen.
3. Das Modell bewerten:
Eine lineare Funktion eignet sich gut als Modell für den Benzinverbrauch eines Autos. Der
tatsächliche Benzinverbrauch bzw. die tatsächlichen Benzinkosten können mithilfe dieses
Modells nicht exakt, sondern nur näherungsweise berechnet werden, da der Benzinverbrauch z. B. von der Geschwindigkeit abhängt. Bei einer sehr hohen Geschwindigkeit verbraucht ein Auto im Schnitt mehr als bei einer konstanten Geschwindigkeit von 120 km/h.
Beispiel 2 Modelle in der Geometrie
Wie groß ist die Wasseroberfläche des Starnberger Sees (Fig. 1)?
Mögliche Lösung:
1. Übersetzen der Situation in ein mathematisches Modell:
Da die Wasseroberfläche des Sees kein Vieleck ist, lässt sie sich nicht so einfach exakt berechnen. Durch Dreiecke und Vierecke, deren Fläche man berechnen kann, kann man sich
allerdings der tatsächlichen Fläche annähern. Das einfachste Modell ist hierbei ein Rechteck, das so gewählt ist, dass es ungefähr der Fläche des Sees entspricht.
2. Mit dem Modell rechnen:
Das eingezeichnete schwarze Rechteck (Fig. 1) hat die Maße 0,7 cm und 3,5 cm.
Da der Maßstab 1 : 500 000 ist, ist die gesuchte Fläche in der Realität
A = 350 000 cm · 1 750 000 cm = 3,5 km · 17,5 km = 61,25 km2.
3. Das Modell bewerten:
Im Internet wird die Wasseroberfläche des Starnberger Sees mit etwa 57 km2 angegeben.
Der entstandene relative Fehler (61,25 – 57) : 57 ≈ 0,075 = 7,5 % ist für die grobe Näherung
der gesuchten Fläche über nur ein Rechteck relativ klein. Wesentlich genauer, aber auch
aufwändiger, wäre die Annäherung der Fläche durch mehrere Rechtecke und Dreiecke.
VI Kompetenzen trainieren und vertiefen
Beispiel 3 Stochastische Modelle
Peter und Robert werfen mit einer Reißzwecke. Peter schlägt vor: „Wir werfen die Reißzwecke jeweils dreimal. Landet sie gar nicht auf dem ‚Kopf’, hast du gewonnen, und landet sie genau zweimal auf dem ‚Kopf’, habe ich gewonnen.“ Wer hat bei diesem Spiel die
besseren Gewinnchancen?
Mögliche Lösung:
1. Übersetzen der Situation in ein mathematisches Modell:
Zunächst einmal muss man herausfinden, wie groß die Wahrscheinlichkeit für „Kopf“
beim einmaligen Wurf einer Reißzwecke ist. Hierfür kann man eine Reißzwecke insgesamt 1000-mal werfen (jeder Schüler der Klasse wirft beispielsweise etwa 35-mal) und die
relative Häufigkeit für „Kopf“ bestimmen.
Von den 1000 Würfen ist die Reißzwecke 398-mal „auf dem Kopf“ gelandet. Die relative
398
Häufigkeit hierfür ist also _
1000 = 0,398 = 39,8 %.
Aufgrund dieser experimentell bestimmten Häufigkeit wird p = 40 % als Trefferwahrscheinlichkeit festgelegt, wobei eine Landung auf dem „Kopf“ ein Treffer sein soll.
2. Mit dem Modell rechnen:
Zur mathematischen Lösung des Problems
wird ein Ausschnitt eines Baumdiagramms
0,6
0,4
gezeichnet.
Die Wahrscheinlichkeit für das Ereignis
0
1
„keinmal Kopf “ ist nach der Pfadregel:
0,6 · 0,6 · 0,6 = 0,63 = 0,216 = 21,6 %.
0,6
0,4
0,6
0,4
Die Wahrscheinlichkeit für das Ereignis
„genau zweimal auf dem Kopf landen“ ist
0
1
0
1
nach der Pfad- und Summenregel:
0,6
0,4
0,4
3 · 0,42 · 0,6 ≈ 0,288 = 28,8 %.
Die Gewinnchancen sind mit jeweils we1
1
0
0
niger als 30 % für Peter und Robert relativ
0 Treffer
genau 2 Treffer
klein, aber die größeren Gewinnchancen
hat Peter mit 28,8 %.
3. Das Modell bewerten:
Eine Unsicherheit des Modells ist die aufgrund eines häufig durchgeführten Versuchs geschätzte Wahrscheinlichkeit von 0,4 für das Ereignis „auf dem Kopf landen“. Ändert man
diese Wahrscheinlichkeit auf z. B. p = 0,39, ändern sich die gesuchten Gewinnchanchen
von Robert von 21,6 % auf ungefähr 22,7 % und von die von Peter von 28,8 % auf ungefähr
27,8 %. Der Unterschied zwischen den Gewinnchanchen ist also nicht mehr ganz so eindeutig.
Fehlende Wahrscheinlichkeiten näherungsweise experimentell
bestimmen!
Nur die nötigen Pfade
des Baumdiagramms
zeichnen!
Vorraussetzungen und
deren Auswirkung auf
das Ergebnis klar machen!
130°
125°
120°
105°
110°
115°
50°
Banff
Vancouver Island
Vancouver
Nanaimo
C. Flattery
Saskatoon
Calgary
C
Kelowna
Penticon
Lethbridge
E
Victoria
Medicine Hat
Regina
G
Weyburn
N
Seattle
WASHINGTON
E
D
mat
h
A
Butte
so
ur
i
Williston
NOR
M O N T A N A
r
O R E G O N
Boise
Sheridan
IDAHO
n
a
k
Idaho Falls
e
W Y O M I N G
Pocatello
R A
E R
S I
Rock Springs
Mt. Elbert
N E W
Santa Fe
Mesa
Lu
P
Las Cruces
e
c
El Paso
Ciudad Juárez
o
Fig. 1
s
G
M
Odessa
San An
U
L
B
F
Hermosillo
a
a
203
A
C
L
F
r
n
O
M
E
X
I
A
110°
500
I
Torre�n
N
i a
R
115°
Nu
o n c
I
f o
l i
N
Cuidad Obreg� n
C
C
A
o s
F
j a
E
Chihuahua
O
120°
a
M E X I C O
Cabo Falso
0
n
C a
Gra
o
l
L
A R I Z O N A
Tucson
VI Kompetenzen trainieren und vertiefen
C
A r k
Trinidad
Gallup
nde
NE
Isla Cedros
O
Colorado Springs
Pueblo
Albuquerque
Phoenix
la
Gi
Yuma
Punta Eugenia
C
t
at
Rio
AN
d o
o r a
CH
San Bernardino
Los Angeles
Long Beach
IS
LA
ND
S
San Diego
GULF OF
SANTA CATALINA Ti�uana Mexicali
Ensenada
Pl
C
Santa Barbara
25°
I
S.
Durango
Isla de Guadalupe
F
Scottsbluff
e
Denver
C O L O R A D O
Saint George
Douglas
I
tt
Las Vegas
30°
C
la
Boulder
Grand Junction
Mt. Whitney
Bakersfield
Pt. Arguello
P
Fort Collins
o
ad
lor
Co
U T A H
.
Laramie
Cheyenne
Salt Lake City
NEVADA
D A
V A
N E
Fresno
Ogden
Sparks
Carson City
Rapid Ci
SOU
P
Casper
N
Great
Salt
Lake
Elko
CALIFORNIA
P A
w d
e
S
Klamath Falls
Reno
Oakland
35°
Tropic of
Cancer
Bis
Miles City
Billings
Bend
Twin Falls
Sacramento
Salinas
Pendleton
is
Redding
San José
Herr Becker fährt mit dem Auto um 8 Uhr morgens mit einer Geschwindigkeit von
60 km/h etwas nördlich von Wiesbaden in Richtung Köln los. Frau Becker startet 40 Minuten später, aber mit 90 km/h. Köln liegt 150 km entfernt. Kann Frau Becker ihren Mann
noch vor Köln einholen, falls beide ihre Geschwindigkeiten beibehalten?
M
Helena
o
la
Lewiston
h
K
Eureka
C. Medocino
S a c ra m e n t o
40°
San Francisco
2
S
A
C
1
Missoula
Richland
C
Salem
Eugene
Bestimme mithilfe eines Atlasses näherungsweise die Fläche des US-Staates Kalifornien (Fig. 1). Recherchiere im Internet oder in geeigneter Fachliteratur nach der tatsächlichen Größe von Kalifornien und vergleiche sie mit deinem Ergebnis.
Havre
R
Mt.Rainier
Yakima
Columbi
a
Portland
C
Aufgaben
Kalispell
Spokane
A
Olympia
45°
105°
1000 Miles
C
3
Ricarda und Katharina werfen 20 aneinander befestigte Heftklammern. Ricarda
schlägt vor: „Wir werfen den Block aus 20 Heftklammern viermal. Landen die Heftklammern genau zweimal mit der Fläche nach unten, gewinnst du, landen sie genau viermal
mit der Fläche nach unten, gewinne ich. In jedem anderen Fall fangen wir noch einmal
von vorne an. Der Verlierer muss dem Sieger ein Eis spendieren.“ Sollte sich Katharina auf
das Spiel einlassen?
4
Ulla hat Wasser zum Kochen gebracht
Temperatur (in °C)
60
und den Temperaturanstieg protokolliert.
Die gemessenen Daten hat sie in ein Koor50
dinatensystem eingetragen.
40
a) Lies Daten aus dem Punktediagramm in
30
Fig. 1 ab und gib eine Funktionsgleichung
20
an, die die Temperatur in Abhängigkeit der
10
Zeit näherungsweise beschreibt.
Zeit (in min)
b) Wie heiß ist das Wasser nach 20 MinuO
1 2 3 4 5 6 7 8
ten?
Fig. 1
c) Nach wie vielen Minuten kocht das Wasser? Löse rechnerisch.
d) Wieso liegen die Punkte des Diagramms in Fig. 1 nicht genau auf einer Geraden?
5 p Marias Moped hat einen Benzintank, der 7 ø fasst. Sie will einen Freund besuchen,
der 2 km entfernt wohnt. Das Moped verbraucht ungefähr 0,1 ø Benzin pro km. Ehe Maria
abfährt, tankt sie voll. Sie tankt 4,5 ø Benzin, das 1,27 € pro Liter kostet. Erkläre, was mit
den folgenden Termen berechnet werden kann.
a) 2 · 0,1
b) 7 : 0,1
c) Stelle selber mindestens zwei Terme zum Sachverhalt auf und lasse deinen Nachbarn
seine Bedeutung finden.
6
Formuliere eine passende Aufgabenstellung zu dem Baumdiagramm in Fig. 2.
7
In der ersten Jahreshälfte des Jahres
2007 war der größte Mann der Welt 2,36 m
groß. Er kommt aus China und heißt Bao
Xishun. Welche Konfektionsgröße und
Schuhgröße benötigt er und wie hängen
diese mit der Körpergröße zusammen?
Eine Recherche über den Zusammenhang
von Körpermaßen und Konfektionsgrößen
ist hilfreich.
8
Bao Xishun
204
Zu jeder Bergetappe eines Radrennens
gehört ein Höhenprofil. Den Profis geht es
wie euch: Bergauf brauchen sie für eine
Strecke deutlich länger als für dieselbe
Strecke abwärts.
a) Beschreibe das Höhenprofil aus Fig. 3.
b) Skizziere einen Graphen für die Zuordnung Zeit ¥ Geschwindigkeit.
c) Skizziere einen Graphen für die Zuordnung Zeit ¥ Weg.
VI Kompetenzen trainieren und vertiefen
40 %
25 %
75 %
60 %
90 %
10 %
Fig. 2
Höhe
Weg
Start
Ziel
Fig. 3
9
Ali fährt mit dem Fahrrad zu seiner Oma und fährt zunächst recht gemütlich. Auf halber Strecke merkt er, dass er sich beeilen muss. Er gibt dann Gas und fährt mit doppelter
Geschwindigkeit. Zeichne zu diesem Sachverhalt einen zugehörigen Graphen.
10
Ein Zeppelin ist ein mit Helium gefülltes, starres Luftschiff. Helium besitzt eine
geringere Dichte als Luft und kann deshalb
das Luftschiff tragen.
Der Transportzeppelin vom Typ „Cargolifter“ hat ein Leergewicht von 5400 kg und umschließt ein Volumen von 7000 m3. Die 7000 m3 Luft wiegen etwa 8429 kg, sodass der mit
Luft gefüllte Zeppelin etwa 13 829 kg wiegt. Ein Kubikmeter Helium wiegt etwa 1,03 kg weniger als ein Kubikmeter Luft. Beim Einfüllen des Heliums wird der Zeppelin also immer
leichter. Ist seine Dichte geringer als die Dichte der Luft, kann er schließlich aufsteigen.
a) Um wie viel Kilogramm wird der Zeppelin leichter, wenn man 300 m3 Helium einfüllt?
b) Das Gewicht des Zeppelins hängt von dem Volumen des eingefüllten Heliums ab. Mit
welcher Gleichung kann man die Funktion eingefülltes Volumen von Helium ¥ Gewicht des
Zeppelins beschreiben und was bedeuten die Variablen in dieser Funktionsgleichung?
c) Zeichne den zur Funktionsgleichung in b) gehörenden Graphen.
d) Der Zeppelin soll eine Ladung mit einem Gewicht von ca. 1600 kg transportieren.
Wie verändert sich der zugehörige Graph? Begründe.
e) Wie viele Kubikmeter Helium müssen in den beladenen Zeppelin aus d) mindestens
eingefüllt werden, damit er eine geringere Dichte besitzt als Luft und damit aufsteigt.
Die Dichte berechnet
sich aus Masse/Volumen. Dichte von Luft:
r = 1,2041 kg/m3.
11
Welcher Wurfgegenstand passt zu welchem Diagramm, wenn in den Diagrammen die
Wahrscheinlichkeiten für die Ereignisse, eine bestimmte Augenzahl zu würfeln, in Prozent
angegeben werden? Begründe. Wie müssten die Achsen der Diagramme beschriftet werden? Zeichne für den vierten Wurfgegenstand ein passendes Diagramm.
(1)
(2)
(4)
(3)
6
5
b)
a)
1
2
3
4
5
6
4
c)
1
2
3
4
5
6
1
2
3
4
5
6
12
Metall dehnt sich aus, wenn man es erhitzt, und es zieht sich zusammen, wenn man
es abkühlt. Bei einem 10 m langen Stahlträger verändert sich die Länge um 1,15 mm, wenn
sich die Temperatur um 10 °C ändert. Der Berliner Funkturm hat bei 20 °C eine Länge von
150 m. Das Gerüst ist aus Stahl gefertigt. Wie groß ist der Längenunterschied des Turms
zwischen Winter (– 15 °C) und Sommer (+ 30 °C)?
13
Satelliten, deren Geschwindigkeit so groß ist, dass sie für einen Erdumlauf genau 24
Stunden benötigen, scheinen durch den Gleichlauf mit der Erde fest am Himmel zu stehen. Wie hoch steht ein solcher geostationärer Satellit, wenn er sich mit einer Geschwindigkeit von 3,07 km/s bewegt? Welche Modellannahmen werden gemacht?
Aus den Lernstandserhebungen 2005
Der Radius des Äquators beträgt 6 398 km.
VI Kompetenzen trainieren und vertiefen
205
8 Abschlusstest
Jetzt hast du fleißig geübt und fühlst dich hoffentlich gut vorbereitet auf diesen
Abschlusstest. Auf den folgenden vier Seiten kommen Aufgaben zu allen Themenbereichen vor. Du kannst den Test in einem Durchgang bearbeiten oder auch in zwei oder drei
kleineren Phasen. Nach jeder Phase oder spätestens, wenn du alle Aufgaben bearbeitet
hast, solltest du deine Lösungen mithilfe der Seiten 247 bis 250 korrigieren. Nach der Korrektur kannst du selbst einschätzen, ob du genug gelernt hast und dich im Vergleich zum
Beginn dieses Kapitels verbessert hast oder ob du noch mehr üben solltest.
1
a) Gib zu der farbigen Fläche der beiden Figuren je zwei passende Terme an
und zeige, dass alle vier Terme äquivalent
sind.
b) Skizziere die rechte Fig. ins Heft und
schraffiere die Fläche, die sich beschreiben
lässt durch (a + b) · (2 b + a) – (a b + b2).
b2
ab
ab
b2
ab
b2
ab
b2
b
a
b
b
a+b
2
Aus der Lernstandserhebung 2004
Ein Drache ist ein Viereck, bei dem eine Diagonale Symmetrieachse
des Vierecks ist.
3
__
D
A
50°
110° E
e
B
Aus der Lernstandserhebung 2007
206
Beim Skispringen werden sowohl die Haltung als auch die Weite des Sprungs bewertet. Fünf Sprungrichter bewerten die Haltung des Springers. Jeder Sprungrichter kann
maximal 20 Punkte vergeben. In den offiziellen Regeln steht: „Die höchste und niedrigste
Note aus der Bewertung der fünf Sprungrichter werden gestrichen. Die verbleibenden
drei Noten werden addiert.“ Die Summe dieser drei Noten ist die Haltungsnote.
a) Die Ergebnisse vom 1. Januar 2004 steSportler Sprungrichterpunkte
Haltungsnote
hen in der Tabelle. Berechne die fehlenden
Pettersen 18,0 17,5 18,5 17,0 18,5 54 Punkte
Haltungsnoten von Höllwarth und Späth.
Höllwarth 19,5 19,0 19,0 19,5 19,0
Späth
18,5 18,5 18,5 18,5 18,5
b) Beate weiß, dass ihr Lieblingsspringer
Beispiel: 17,0 ; 18,5
Hannawald 55 Punkte als Haltungsnote
18,0 + 17,5 + 18,5 = 54
erhalten hat.
Wie könnten die fünf Sprungrichter gepunktet haben?
c) Nimm nun an, dass die Haltungsnoten nicht wie in der Tabelle, sondern als arithmetisches Mittel der fünf Sprungrichterpunkte ermittelt werden. Berechne unter dieser Voraussetzung die Haltungsnoten von Pettersen und Höllwarth.
Außer der Haltung wird auch die Sprungweite bewertet. Für die Sprungweite erhält ein
Sportler 60 Punkte, wenn er genau 115 m weit springt. Springt er weiter, erhält er einen
Zuschlag von 1,8 Punkten je Meter. Springt er kürzer, erhält er einen Abzug von 1,8 Punkten je Meter.
d) Pettersen sprang 123 m weit, Hannawald sprang 112 m weit. Berechne, wie viele Punkte
sie für ihre Weiten bekamen.
e) Gib einen Term für die Berechnung der Punkte an, die es für die Sprungweite gibt.
Das Viereck ABCD ist eine Raute und das Viereck ABED ein Drachen mit der Strecke
AE als Symmetrieachse. Bestimme den Winkel e. Begründe ausführlich.
C
4
Am 18. 03. 1999 bauten die Einwohner von Hampsville (USA) aus 304 756 Legosteinen
einen 21,37 m hohen Turm. Ein Legostein wiegt etwa 2,75 g. Wie viele Schülerinnen und
Schüler deiner Jahrgangsstufe bräuchtest du etwa, um den Turm auf einmal anzuheben?
Begründe rechnerisch. Welche Annahmen hast du getroffen?
VI Kompetenzen trainieren und vertiefen
Lösungen auf Seite 247–250.
5
Rebecca schneidet aus Pappe verschieden große Rechtecke aus. Sie misst die Seitenlängen, berechnet die Flächeninhalte und wiegt dann die Rechtecke. Die gefundenen
Werte trägt sie in ein Koordinatensystem ein (Fig. 1).
a) Ist die Zuordnung Flächeninhalt ¥ GeGewicht (in g)
wicht proportional? Begründe.
3
b) Wie kommt es, dass die Punkte nicht
2
genau auf einer Geraden liegen?
c) Wie schwer wird ein Papprechteck mit
Flächeninhalt
1
(in cm2)
dem Flächeninhalt 1 m2 ungefähr sein?
d) Welche Fläche wird ein Papprechteck
O
10 20 30 40 50 60 70 80
ungefähr haben, das 1200 g wiegt?
Fig. 1
6
Von einem Heißluftballon aus werden
die Orte A und B unter den Winkeln
a ≈ 66° und b ≈ 24° angepeilt. Die Orte
A und B liegen 2 700 m voneinander entfernt. Wie hoch schwebt der Ballon über
dem Punkt G? Zeichne das Dreieck ABC in
einem selbst gewählten Maßstab in dein
Heft und miss die gesuchte Höhe.
C
b
a
G
A
B
10
7
Alexandra „würfelt“ mit einer Sechskantmutter (Fig. 2) Zahlen von 1 bis 8.
a) Welche Schätzung (vergleiche Tabelle) der Wahrscheinlichkeiten für die Zahlen 1 bis 8
passt zu der Sechskantmutter? Begründe.
b) Berechne mit der von dir gewählten Schätzung aus a) die Wahrscheinlichkeit dafür, in
drei Würfen nur ungerade Zahlen zu „würfeln“.
Augenzahl
1
2
3
4
5
6
7
8
Schätzung A für Wahrsch. in %
35
5
5
5
5
5
5
35
Schätzung B für Wahrsch. in %
12,5
12,5
12,5
12,5
12,5
12,5
12,5
12,5
Rückseite 8
2
7
3
1
4
6
5
Fig. 2
8
Herr Barth rasiert sich seit seinem 17. Geburtstag täglich. Wie alt wird Herr Barth sein,
wenn er eine Fläche rasiert hat, die so groß ist wie sein 15 m langer und 8 m breiter Rasen?
9
Der Body Mass Index (BMI) stellt eine
Beziehung zwischen der Körpergröße eines
Menschen und seinem Gewicht her. Lies
die Antworten zu den folgenden Fragen
aus Fig. 3 ab.
a) Wie viel kg wiegt ein Mensch, der 1,80 m
groß ist und einen BMI von 25 besitzt?
b) Wie viel kg sollte man mindestens und
höchstens wiegen, wenn man 1,65 m groß
ist?
c) Paul wiegt 70 kg und behauptet, dass
sein BMI optimal ist. Wie groß könnte Paul
sein?
Lösungen auf Seite 247–250.
Körpergewicht (in kg)
140
BMI 35
Beispiel:
130
72,25 kg
——
= BMI 25
120
BMI 30
(1,70m)2
110
BMI 25
100
90
BMI 20
80
70
Gewicht in kg
BMI: ———
60
(Größe in m)2
50
Körpergröße (in m)
40
1,50 1,60 1,70 1,80 1,90 2,00
Fig. 3
Der BMI errechnet sich
aus Körpergewicht
in Kilogramm geteilt
durch die Körperlänge
in Metern zum Quadrat.
So lässt sich ablesen,
in welche Risikogruppe jemand fällt. Die
Weltgesundheitsorganisation hält einen BMI
zwischen 20 und 25 für
optimal. Andererseits
gibt es Hinweise, dass
auch der Bereich zwischen 25 und 30 noch
gesund ist.
VI Kompetenzen trainieren und vertiefen
207
10
Fettgehalt:
Leberwurst
40 %
Schokolade
31 %
Pommes frites 15 %
Kirschtorte
Kotelett
Milch
14 %
11 %
3,5 %
Vollkornbrot
1%
Fig. 1
Die Tabelle (Fig. 1) zeigt den Fettgehalt einiger Lebensmittel an. Ein Mann sollte nicht
mehr als 85 g, eine Frau nicht mehr als 70 g Fett täglich essen.
a) Wie viel Gramm dieser Nahrungsmittel dürfte ein Mann bzw. eine Frau täglich höchstens essen? Trage deine Ergebnisse in eine Tabelle ein.
b) Herr Paulus hatte folgendes Menü: 250 g Pommes frites, 180 g Kotelett, 400 g Milch.
Wie viel Gramm Schokolade sind demnach noch erlaubt?
11
Jedes Jahr sterben 40 700 Personen durch das Rauchen in Deutschland. Das bedeutet,
dass in Deutschland etwa alle 13 Minuten eine Person durch Tabak stirbt. Weltweit fangen 90 000 Jugendliche täglich mit dem Rauchen an. Das Diagramm in Fig. 2 veranschaulicht die Entwicklung der jugendlichen Raucher in Deutschland. Welche der folgenden
Behauptungen sind wahr?
Das Diagramm zeigt, dass
a) der Anteil der rauchenden Jungen zwischen 41 % und 54 % variiert,
b) im Jahr 1979 _52 aller Mädchen rauchten,
c) während einer Periode in den 90er-Jahren keine Mädchen rauchten,
d) 1973 im Vergleich zu 1993 ein doppelt so hoher Anteil Mädchen rauchte,
e) der Anteil der Raucher bei Mädchen bzw. Jungen gleichzeitig stieg,
f) jedes Jahr ein größerer Anteil Jungen als Mädchen rauchte,
g) 1982 der Anteil der Jungen, die rauchten, am geringsten war,
h) es von 1983 – 1993 viele Mädchen gab, die mit dem Rauchen aufhörten,
i) es 1992 im Vergleich zu 1986 anteilig mehr Jungen gab, die rauchten.
Anteil der Jugendlichen in Deutschland, die jeden oder fast jeden Tag rauchen:
Anteil in Prozent
Daten: Bundeszentrale für
54
gesundheitliche Aufklärung
52
Jungen
50
48
Mädchen
46
44
42
40
38
Jahr
36
1970 1972 1974 1976 1978 1980 1982 1984 1986 1988 1990 1992 1994 1996 1998 2000
Fig. 2
12
Paul bekommt von seiner Großmutter 5000 € geschenkt. Er legt das Geld zu einem
Zinssatz von 2,5 % auf einem Sparbuch an.
a) Wie hoch ist das Guthaben nach einem Jahr?
b) Über welchen Betrag könnte er nach einem halben Jahr verfügen?
c) Wie hoch ist das Guthaben nach drei Jahren, wenn die Zinsen auf dem Konto mitverzinst werden?
13
100 Roggenkörner wiegen ungefähr
3 g. Wie viele Roggenbrote kann man wohl
aus dem Korn eines 1 ha großen Roggenfeldes backen? Erkläre, wie du vorgegangen
bist, und überlege, wie du überprüfen
kannst, ob deine Schätzung realistisch ist.
208
VI Kompetenzen trainieren und vertiefen
Lösungen auf Seite 247–250.
14
8
16
19
4,5
Re
13
is
6
10
12
27
26
Reis
8
8
5
Reis
Die Schüler der 8c hatten die Aufgabe,
Verpackungen für ein Kilogramm Reis zu
basteln. Jede Verpackung muss so beschaffen sein, dass ein Kilogramm Reis hineinpasst, sie aber nicht so groß ist, dass sie
befüllt mehr als 15 % des Verpackungsvolumens Luft enthält.
a) Entsprechen alle Reisverpackungen den
Anforderungen?
b) Für welche Verpackung wurde am wenigsten Pappe benötigt? (Klebekanten sollen nicht eingerechnet werden.)
32
Re
is
7
20
15
Familie Hartung möchte sich ein neuBenzinversion
es Auto kaufen. Nachdem sie sich für ein
· monatliche Festkosten: 174,40 €
Modell entschieden haben, müssen sie
· Steuern und Versicherung monatlich: 16,55 €
sich nur noch überlegen, ob sie die Diesel· Kraftstoffkosten je Kilometer: 0,12 €
oder Benzinversion dieses Modells kaufen
möchten. In einer Autozeitschrift haben sie
gelesen, dass die monatlichen Festkosten
für die Benzinversion ihres Wunschmodells inklusive Steuer- und Versicherungen 190,95 €
betragen. Die Kraftstoffkosten je Kilometer betragen bei dieser Benzinversion 0,12 €. Ein
Bekannter, der die Dieselversion des gewünschten Modells besitzt, erzählt ihnen, dass
er im letzten Monat, bei 960 zurückgelegten Kilometern, 307,70 € Kosten inklusive Festkosten, Steuern und Versicherung und im Monat davor, bei 1240 gefahrenen Kilometern,
330,10 € für alles bezahlt hat.
a) Wie viel kostet bei der Dieselversion der Kraftstoff pro Kilometer?
b) Stelle je eine Gleichung für die Funktion gefahrene Kilometer ¥ monatliche Gesamtkosten auf und zeichne die zugehörigen Graphen der Funktionen.
c) Wie viele Kilometer muss die Familie Hartung im Monat mindestens fahren, damit sich
die Dieselversion lohnt? Löse zeichnerisch und rechnerisch.
16
In einer Lostrommel befinden sich Treffer und Nieten. Die genauen Zahlen sind nicht
bekannt. Beantworte die folgenden Fragen. Gib jedes Mal ein einfaches Beispiel an, um
deine Vermutung zu überprüfen.
a) Wie ändert sich die Gewinnwahrscheinlichkeit, wenn man die Anzahl der Nieten
verdoppelt?
b) Wie ändert sich die Gewinnwahrscheinlichkeit, wenn man die Anzahl der Treffer
verdoppelt?
c) Wie ändert sich die Gewinnwahrscheinlichkeit, wenn man die Anzahl der Treffer
und der Nieten halbiert?
17
Wie lang ist die Schnur, aus der die
Schnecke in Fig. 1 gerollt wurde, ungefähr,
wenn der Durchmesser der Schnecke etwa
7 cm beträgt?
Lösungen auf Seite 247–250.
Fig. 1
VI Kompetenzen trainieren und vertiefen
209
3
Kapitel VI, Abschlusstest
d1
Seite 206
D
100°
d2
30°
1
individuelle Lösung, z.B.:
a) zu Fig. 1: (I) 4 b2 + 4 a b; (II) (a + 2 b)2 – a2
zu Fig. 2: (III) 4 b (a + b); (IV) 2 b (a + b) + 2 a b
A
Um die Äquivalenz der Terme (I) bis (IV) zu zeigen, werden
alle Terme so weit wie möglich vereinfacht:
(I) 4 b2 + 4 a b lässt sich nicht mehr weiter vereinfachen.
(II) (a + 2 b)2 – a2 = a2 + 4 a b + 4 b2 – a2 = 4 b2 + 4 a b und ist
damit äquivalent zu Term (I).
(III) 4 b (a + b) = 4 a b + 4 b2 und ist damit äquivalent zu
Term (I).
(IV) 2 b (a + 2 b) + 2 a b = 2 a b + 4 b2 + 2 a b = 4 a b + 4 b2 und
ist damit äquivalent zu Term (I).
Die Terme (I) bis (IV) sind also alle äquivalent zueinander.
b) Durch den Term (a + b) (2b + a) – (a b + b2) wird die gelb
schraffierte Fläche beschrieben.
110°
50°
100°
b B
30°
E
50°
C
c
e
Zunächst einmal werden b und d1 bestimmt. Da die Strecke
durch A und E die Symmetrieachse des Drachens ist, müssen
b und d1 gleich sein. Da außerdem die Winkelsumme im Viereck 360° beträgt, muss gelten:
b = d1 = (360° – 110° – 50°) : 2 = 100°.
Da das Viereck ABCD eine Raute ist und in einer Raute die gegenüberliegenden Winkel gleich groß sind,
beträgt c = 50°. Außerdem muss dann d2 = e gelten, weil
sonst die anderen beiden gegenüberliegenden Winkel der
Raute nicht gleich wären.
Da die Winkelsumme der Raute ABCD 360° beträgt, muss
gelten:
e = d2 = (360° – 2 · 100° – 2 · 50°) : 2 = 60° : 2 = 30°.
Der gesuchte Winkel e beträgt also 30°.
4
b
a+b
b
a+b
2
a) Haltungsnote Höllwarth: 19 + 19,5 + 19 = 57,5
Haltungsnote Späth: 18,5 + 18,5 + 18,5 = 55,5
b) individuelle Lösung, z.B.:
mögliche Wertung der fünf Sprungrichter für Hannawald mit
der Haltungsnote 55 Punkte: 19,0; 18,5; 18,0; 17,0; 18,5.
c) Pettersen: (18 + 17,5 + 18,5 + 17 + 18,5) : 5 = 17,9
Höllwarth: (19,5 + 19 + 19 + 19,519) : 5 = 19,2
d) Pettersen: 74,4 Punkte,
denn er sprang 123 m = 115 m + 8 m; also erhielt er 60 Punkte + 8 · 1,8 Punkte = 74,4 Punkte für seine Sprungweite.
Hannawald: 54,6 Punkte,
denn er sprang 112 m = 115 m – 3 m; also erhielt er 60 Punkte – 3 · 1,8 Punkte = 54,6 Punkte für seine Sprungweite.
e) Sind P die Punkte und x die Sprungweite, dann gilt:
P (x) = 60 + 1,8 (x – 115).
Am Beispiel aus d):
P (123) = 60 + 1,8 (123 – 115) = 74,4 und
P (112) = 60 + 1,8 (112 – 115) = 54,6
individuelle Lösung, z. B.:
Antwort: Man benötigt etwa 25 Schüler.
Begründung: Zunächst einmal wird das Gewicht des Turms
bestimmt: Da ein Legostein 2,75 g wiegt und insgesamt
304 756 Legosteine benutzt wurden, wiegt der Turm:
2,75 g · 304 756 = 838 079 g = 838,079 kg.
Da ein Kind in der achten Klasse etwa 20 bis 60 kg tragen
kann, rechnet man:
838,079 kg : 20 kg ≈ 42 und 838,079 kg : 60 kg ≈ 14.
D. h., dass man zwischen 14 und 42 Schüler zum Tragen des
Turmes oder der Legosteine (den Turm mit über 21 m Höhe
kann man so natürlich nicht tragen!) benötigt.
Die dafür getroffenen Voraussetzungen waren, dass ein Achtklässler zwischen 20 und 60 kg tragen kann. Werden andere
Annahmen getroffen, ändert sich das Ergebnis entsprechend.
Lösungen
247
Seite 207
5
a) Ja, die Zuordnung „Flächeninhalt des Rechtecks Gewicht“ ist eine proportionale Zuordnung, denn verdoppelt
sich z. B. die Größe der Rechtecks, muss das neue Rechteck
natürlich auch das Doppelte wiegen, da es ja aus der gleichen Pappe sein soll und deshalb pro Flächeneinheit das
gleiche Gewicht haben sollte.
b) Die Punkte liegen nicht exakt auf einer Geraden, da die
Rechtecke wahrscheinlich nicht exakt ausgeschnitten wurden, vielleicht auch die Seitenlängen nicht exakt ausgemessen wurden und wahrscheinlich die Gewichte nicht exakt
gewogen wurden, so dass kleinere Abweichungen der Messwerte von der Geraden auftreten.
c) Aus dem Graphen lässt sich der Punkt (65 | 3) ablesen.
Da es sich um eine Ursprungsgerade handelt, muss sie die
233
Gleichung y = _
65 x besitzen, wobei x der Rechtecksfläche
und y dem zugehörigen Gewicht entspricht.
3
30 000
_ ≈ 461,5, da 1 m2 = 10 000 cm2.
Also y = _
65 · 10 000 =
65
2
Ein 1 m großes Rechteck müsste also ungefähr 462 g wiegen.
3
d) Ansatz: y = 1200 = _
65 x
x = 26 000
Also ist ein 1200 g schweres Rechteck ungefähr
26 000 cm2 = 2,6 m2 groß.
2 3
2
3
2 3
6
Es wird der Maßstab 1 : 50 000 gewählt. Mithilfe der gegebenen Winkel werden die Innenwinkel des Dreiecks bestimmt:
CBA = 24°, da Wechselwinkel zum Winkel b.
¼ ACB = 42°, da 66° – 24° = 42°.
¼ BAC = 114°, da 180° – 42° – 24° = 114°.
Jetzt wird das Dreieck ABC maßstabsgerecht konstruiert und
die Höhe h zur Seite a gemessen:
b
g
24°
°
42
C
66°
h a
11
90°
4°
A
G
2,999 cm
b
5,4 cm
24°
B
h ≈ 3 cm š 1500 m
Der Ballon schwebt etwa 1500 m über dem Punkt G.
7
a) Schätzung A passt zu der Sechskantmutter, da es wahrscheinlicher ist, mit der Mutter eine 1 oder 8 zu würfeln als
eine der anderen Zahlen, da die Fläche der 1 und der 8 gleich
groß und größer als alle anderen Flächen sind.
248
Lösungen
b) Schätzung A: Ungerade sind die Zahlen: 1, 3, 5 und 7, also
ist die Wahrscheinlichkeit dafür, eine ungerade Zahl zu würfeln: 0,35 + 0,05 + 0,05 + 0,05 = 0,5.
Würfelt man dreimal ergibt sich: P = 0,53 = 0,125 = 12,5 %.
Schätzung B: Auch hier ist die Wahrscheinlichkeit für „ungerade“ 0,5, also ist die Wahrscheinlichkeit für „dreimal ungerade“ in drei Würfel ebenfalls 12,5 %.
8
individuelle Lösung, z.B.:
Rasenfläche: 15 m · 8 m = 120 m2
Die Fläche des Bartes muss geschätzt bzw. gemessen werden: Werte zwischen 150 cm2 und 220 cm2 sind realistisch.
Sei die Bartfläche von Herrn Barth etwa 200 cm2.
Berechnung der Anzahl der Tage:
120 m2 : 200 cm2 = 1 200 000 cm2 : 200 cm2 = 6000
Herr Barth rasiert sich also schon seit etwa
6000 Tagen ≈ 16,44 Jahre, also 16 Jahre und 160 Tage. Da
Herr Barth sich ab dem 17. Lebensjahr rasiert, ist er heute
etwa 17 + 16 = 33 Jahre und 160 Tage alt.
9
a) 81 kg
b) Da ein BMI zwischen 20 und 25 optimal ist, sollte man mit
einer Körpergröße von 1,65 m mindestens 55 kg und höchstens 68 kg wiegen. Da auch ein BMI von 30 noch gesund ist,
sollte man mit dieser Körpergröße maximal 82 kg wiegen.
c) Paul könnte zwischen 1,87 cm und 1,68 cm groß sein, damit
sein BMI zwischen 20 und 25 liegt und damit optimal ist.
Seite 208
10
a) Gegeben: Prozentsatz p und Prozentwert W
W
Gesucht: Grundwert G = _
p
Gerundet erhält man die folgenden Ergebnisse:
Speise
Mann
Frau
L
213
175
S
274
226
P
567
467
Ki
607
500
Ko
773
636
M
2429
2000
V
8500
7000
b) Gegeben: p und G, gesucht: W = p · G
Der Fettgehalt des angegebenen Menüs beträgt also:
0,15 · 250 g + 0,11 · 180 g + 0,035 · 400 g = 71,3 g
Es bleiben höchstens noch 85 g – 71,3 g = 13,7 g Fett, die
Herr Paulus an diesem Tag essen dürfte.
Berechnung der Schokoladenmenge:
W
Gegeben: p, W, gesucht: G = _
p
Die Schokoladenmenge beträgt also: 13,7 : 0,31 ≈ 44 g.
11
a) Wahr, das Maximum des Graphen liegt bei 54 % und das
Minimum bei 41.
b) Wahr, denn zum Jahr 1979 rauchten 40 % = 0,4 = _25 der
Mädchen.
c) Falsch, denn das Minimum des Graphen der Mädchen
liegt bei 36 % im Jahre 1993.
d) Falsch, im Jahre 1973 waren es 47 % Mädchen, die rauchten und im Jahre 1993 nur 36 %, aber nicht 23,5 %, was der
Hälfte des Anteils von 1973 entsprechen würde.
e) Wahr, der Anteil der Jungen und der Mädchen stieg im
Jahre 1982 und auch im Jahre 1993 an.
f) Wahr, der Graph der Jungen liegt in jedem Jahr über dem
Graphen der Mädchen.
g) Falsch, der Anteil der rauchenden Jungen war im Jahre
1993 mit 41 % am geringsten.
h) Wahr, denn zunächst einmal stieg zwar der Anteil der
rauchenden Mädchen bis 1986 und fiel dann bis 1993 stark
ab. Im Zeitraum von 1989 bis 1993 hörten also viele Mädchen
mit dem Rauchen auf, wenn man davon ausgeht, dass die
Gesamtanzahl der Mädchen in Deutschland sich in diesem
Zeitraum nicht wesentlich veränderte.
i) Falsch, 1986 rauchten 46 % der Jungen wohingegen 1992
nur 42 % der Jungen rauchten.
12
a) Gegeben: p = 2,5 % = 0,025; G = 5000 €
Gesucht: Zinsen Z = G · p
Also Z = G · p = 5000 € · 0,025 = 125 €
Antwort: Nach einem Jahr beträgt das Guthaben
5000 € + 125 € = 5125 €.
b) Jahreszinsen Z = 125 €. Also betragen die Zinsen für ein
halbes Jahr 125 € : 2 = 62,50 €.
Antwort: Nach einem halben Jahr kann er also über einen
Betrag von 5062,50 € verfügen.
c) Wenn die Zinsen mitverzinst werden, hat Paul nach drei
Jahren ein Kapital von
K = (1 + p)x · G = (1 + 0,025)3 · 5000 € ≈ 5384,45 €
auf dem Konto.
13
individuelle Lösung, z. B.:
In jeder Ähre befinden sich etwa 30 bis 50 Roggenkörner
und auf einem Quadratmeter Feld wachsen etwa 400 bis
800 Halme. Ein Hektar entspricht 10 000 Quadratmetern, also
kann man pro ha etwa 40 · 600 · 10 000 = 240 000 000 Roggenkörner ernten.
Da 100 Roggenkörner etwa 3 g wiegen,
wiegen die Roggenkörner eines 1 ha großen Feldes
etwa 7 200 000 g = 7200 kg = 7,2 t.
Da ein Roggenbrot etwa 1 kg wiegt und aus etwa 500 g Roggenmehl hergestellt wird, kann man etwa 14 400 Brote aus
dem Korn eines 1 ha großen Feldes machen. Werte zwischen
7200 und 24 000 Broten werden als Lösung akzeptiert.
Seite 209
14
1 kg Reis nimmt ungefähr ein Volumen V = 1140 cm3 ein.
Da bis zu 15 % Luft in einer Schachtel erlaubt sind, darf das
maximale Schachtelvolumen Vmax = 1140 cm3 · 1,15 = 1311 cm3
betragen.
Volumen Schachtel 1 (unten links):
V = G · h = 0,5 · 26 cm · 10 cm · 12 cm = 1560 cm3.
Diese Schachtel ist also zu groß.
Volumen Schachtel 2 (unten rechts):
V=G · h
= (0,5 · 20 cm · 25 cm + 20 cm · 7 cm) · 8 cm
= (250 cm2 + 140 cm2) · 8 cm
= 390 cm2 · 8 cm
= 3120 cm3.
Diese Schachtel ist also viel zu groß.
Volumen Schachtel 3 (oben rechts):
V = VZ1 – VZ2 = G1 · h – G2 · h
= π (9,5 cm)2 · 8 cm – π (9,5 cm – 4,5 cm)2 · 8 cm
≈ 16 39,9 cm3
Die Schachtel ist also ebenfalls zu groß.
Volumen Schachtel 4 (oben links):
V = G·h
= (0,5 · 6 cm · (16 cm – 8 cm) · 0,5 · 2 + 8 cm · 6 cm) · 13 cm
= (24 cm2 + 48 cm2) · 13 cm
= 72 cm2 · 13 cm
= 936 cm3.
Die Schachtel ist also erlaubt.
b) Die Oberflächen der Körper 1 – 4 werden bestimmt. Alle
Längen sind in cm angegeben.
Oberfläche 1 (unten links):
O = 0,5 · 10 · 26 · 2 + 12 · 27,9 + 12 · 26 + 10 · 12 = 1026,8
Ohne Klebekanten werden also 1026,8 cm2 Material benötigt.
Oberfläche 2 (unten rechts):
O = (0,5 · 20 · 25 + 20 · 7) · 2 + 27 · 8 · 2 + 7 · 8 · 2 + 20 · 8
= 1484
Ohne Klebekanten werden also 1484 cm2 Material benötigt.
Oberfläche 3 (oben rechts):
O = 2 · π · 9,5 · 8 + 2 · π · 5 · 8 + 2 (π · 9,52 – π · 52) ≈ 1138,8
Ohne Klebekanten werden also etwa 1138,8 cm2 Material
benötigt.
Oberfläche 4 (oben links):
O = 2 (0,5 · 6 · (16 – 8) · 0,5 · 2 + 8 · 6) + 4 · 13 · 5 + 2 · 13 · 8
= 612
Ohne Klebekanten werden also 612 cm2 Material benötigt.
Für die vierte Verpackung wurde also am wenigsten Material
benötigt.
Lösungen
249
15
a) Monatliche Gesamtkosten y = a x + c, wobei c die Festkosten, x die Anzahl der gefahrenen Kilometer und a die
Kraftstoffkosten pro Kilometer sind.
I: 307,70 = a · 960 + c
II: 330,10 = a · 1240 + c
Gleichung I nach c auflösen:
I: 307,70 = a · 960 + c
| – a · 960
I a:
c = 307,70 – a · 960
I a in II einsetzen:
330,10 = a · 1240 + 307,70 – a · 960
330,10 = 307,70 + 280 · a
| – 307,70
280 a = 22,4
a = 0,08
a = 0,08 in I a einsetzen:
c = 307,70 – 0,08 · 960
c = 230,90
Bei der Dieselversion kostet der Kraftstoff pro Kilometer
0,08 €. (Die Festkosten betragen im Monat 230,90 €.)
b) Benzinversion: y = 0,12 x + 190,95
Dieselversion: y = 0,08 x + 230,90
(x sind hierbei die gefahrenen Kilometer und y die monatlichen Gesamtkosten)
Zur Kontrolle der zeichnerischen Lösung benutze den Funktionsplotter auf der Begleit-CD.
c) Aus der Zeichnung lässt sich entnehmen, dass es sich ab
etwa 1000 km pro Monat lohnt, die Dieselversion zu nehmen,
da dort der Schnittpunkt der beiden Graphen ist und ab da
die Dieselversion billiger wird.
Rechnerisch:
Die Gleichungen aus b) werden gleichgesetzt:
0,12 x + 190,95 = 0,08 x + 230,90
| – 0,08x
0,04x + 190,95 = 230,9
| – 190,95
0,04x = 39,95
| : 0,04
x = 998,75
Die Familie Hartung muss monatlich 998,75 km fahren, damit
sich die Dieselversion lohnt.
16
Sei t die Anzahl der Treffer und n die Anzahl der Nieten in
der Lostrommel mit insgesamt t + n Losen.
a) Die Gewinnwahrscheinlichkeit ändert sich von t : (t + n)
auf t : (t + 2n), verkleinert sich also um das (t + n) : (t + 2 n)
-fache.
Beispiel: 2 Treffer, 8 Nieten
5
2
2
1
_
_
_
p1 = _
10 = 0,2 und p2 = 18 = 9 (das 9 -fache der Gewinnwahrscheinlichkeit 1).
250
Lösungen
b) Die Gewinnwahrscheinlichkeit ändert sich von t : (t + n)
auf 2 t : (2 t + n), vergrößert sich also um das
(2 t : (2 t + n)) : (t : (t + n))-fache.
Beispiel: 2 Treffer, 8 Nieten
5
2
4
1
_
_
_
p1 = _
10 = 0,2 und p2 = 12 = 3 (das 3 -fache der Gewinnwahrscheinlichkeit 1).
c) Die Trefferwahrscheinlichkeit ändert sich nicht,
denn t : (t + n) = 2 t : (2 t + 2 n) = 2 t : (2 (t + n)).
Beispiel: 2 Treffer, 8 Nieten
2
4
_
p1 = _
10 = 0,2 und p2 = 20 = 0,2
Die Trefferwahrscheinlichkeit ändert sich also nicht.
17
individuelle Lösung, z. B.:
Der Radius der Schnurschnecke ist etwa 3,5 cm. Die Schnecke
besteht aus sechs „Kreisen“. Der kleinste Kreis hat etwa den
Radius r1 ≈ 0,6 der danach r2 ≈ 1,2, anschließend r3 ≈ 1,8,
r4 ≈ 2,4, r5 ≈ 3 und r6 ≈ 3,6.
Nun werden die Umfänge der sechs „Kreise“ berechnet und
anschließend addiert um die ungefähre Länge der Schnur zu
bestimmen.
U1 ≈ 2 π · 0,6 ≈ 3,8
U2 ≈ 2 π · 1,2 ≈ 7,5
U3 ≈ 2 π · 1,8 ≈ 11,3
U4 ≈ 2 π · 2,4 ≈ 15,1
U5 ≈ 2 π · 3,0 ≈ 18,8
U6 ≈ 2 π · 3,6 ≈ 22,6
Also ist die Gesamtlänge der Schnur etwa 79,1 cm. Werte zwischen 60 cm und 100 cm sind akzeptabel.
Teste dich selbst – Lösungen
Rechnen mit Zahlen und Variablen
1 Terme
a) falsch – Die Ausdrücke 5 x und 2 sind nicht gleichartig
und dürfen daher nicht zusammengefasst werden. Der Ausdruck 5 x – 2 lässt sich also nicht weiter vereinfachen.
b) richtig – Man muss den Term in Beziehung zur Fläche setzen und so argumentieren: Die blaue Fläche ist ein Rechteck
mit der Breite a – b und der Höhe c + d. Damit ergibt sich
die Fläche A = Breite · Höhe = (a – b) · (c + d).
c) richtig – Nun muss man so argumentieren: Die blaue
Fläche erhält man, indem man von der Fläche des großen
Rechtecks mit den Seitenlängen a und d + c die beiden gelben Rechtecke mit den Seitenlängen b und d bzw. b und c
subtrahiert: A = a · (d + c) – b · d – b · c.
d) falsch – Hier argumentiert man mit den Rechenregeln:
Das Quadrat aus einer Differenz ist nicht gleich der Differenz
der Quadrate. Hier muss die 2. binomische Formel angewendet werden: (3 – x)2 = 9 – 6 x + x2.
e) falsch – Die Ausdrücke a2 und a haben verschiedene Exponenten und sind daher nicht gleichartig, können also nicht
zusammengefasst werden.
f) falsch – Es gilt „Punktrechnung vor Strichrechnung“, daher muss zunächst der Term x · 4 x berechnet werden. Man
erhält mit x · 4 x = 4 x2 und 9 x eine Summe nicht gleichartiger Terme, die sich nicht weiter zusammenfassen lässt.
g) falsch – Man argumentiert mit den Rechenregeln für
Wurzeln: Die Wurzel aus____
einer Summe ist
__ nicht gleich der
__
Summe der Wurzeln: √a + b ≠ √a + √b . Es darf also nicht
für jeden
__ Summanden
__ unter dem Wurzelzeichen die Re√a2 = a bzw. √b2 = b angewendet werden. Der Term
gel
______
√a2 + b2 lässt sich nicht weiter vereinfachen.
h) richtig – Mit Wurzeln rechnet man wie mit reellen Zahlen,
mithilfe
des
__
__ Distributivgesetzes
__
__erhält man:
5 √3 – 2 √3 = (5 – 2) · √3 = 3 √3 .
__
i) richtig – Durch die Erweiterung des Bruches mit √2
lässt sich der__Nenner__„rational machen“ und der Bruch kür__
√2 · 2
√2 · 2
2__ _
√
zen: _
= √__ √__ = _
2 = 2.
√
2
2· 2
2 Gleichungen
a) falsch – Durch Äquivalenzumformungen erhält man:
0,5 + (2 – x) = 1 – (1 + x)
| Klammern auflösen
0,5 + 2 – x = 1 – 1 – x
| zusammenfassen
2,5 – x = – x
|+x
2,5 = 0 (falsch)
Die Gleichung hat keine Lösung. Man kann auch mit der
Einsetzprobe argumentieren: Sie bestätigt, dass – 2 keine
Lösung ist: 0,5 + (2 – (– 2)) = 1 – (1 + (– 2))
4,5 = 2 (falsch)
b) richtig – Durch Äquivalenzumformungen erhält man:
4 (y + 5) = 9 y + 5
| Klammer auflösen
4 y + 20 = 9 y + 5
| – 20
4 y = 9 y – 15
| –9y
– 5 y = – 15
| : (– 5)
y=3
3 ist ein Teiler von 15.
c) richtig – Durch Äquivalenzumformungen erhält man:
x – (x – 7) (x + 7) = 50 – x2 | Klammern ausmultiplizieren
x – (x2 – 49) = 50 – x2 | Klammer auflösen
x – x2 + 49 = 50 – x2 | + x2
x + 49 = 50
| – 49
x=1
1 ist eine einstellige Quadratzahl.
d) richtig – Durch Äquivalenzumformungen erhält man:
(8 – z) (2 + z) = (7 – z) (z + 1) | Klammern ausmultiplizieren
16 + 8 z – 2 z – z2 = 7 z + 7 – z2 – z | zusammenfassen
16 + 6 z – z2 = 6 z + 7 – z2
| + z2
16 + 6 z = 6 z + 7
| –6z
16 = 7 (falsch)
e) falsch – Die Situation muss in ein mathematisches Modell,
hier in einen Term, übersetzt werden: Wenn es 15-mal so viele Schüler wie Lehrer gibt, muss man die Anzahl der Lehrer
mit 15 multiplizieren, um auf die Anzahl der Schüler zu kommen, es gilt also: S = 15 · L.
Eine einfache Zahlenprobe bestätigt dies: Für L = 5
und S = 75 gilt: 75 = 15 · 5 (wahr).
f) falsch – Man kann mit den bei Gleichungen erlaubten
Operationen und einem Beispiel argumentieren: Das Multiplizieren beider Seiten einer Gleichung mit derselben Zahl
stellt eine Äquivalenzumformung dar, bei der die Lösung
der Gleichung unverändert bleibt. Multipliziert man z. B. die
Gleichung x = 10 mit 4, so erhält man 4 x = 40; auch diese
Gleichung hat die Lösung x = 10.
3 Lineare Gleichungssysteme (LGS)
a) falsch – Zur Lösung dieses Problems wählt man am besten das Additionsverfahren aus:
I + II:
– 3 y = 23 + y + 13 | zusammenfassen
– 3 y = 36 + y
| –y
– 4 y = 36
| : (– 4)
y = –9
Das Einsetzen von y = – 9 in II liefert:
– 2 x = – 9 + 13
| zusammenfassen
–2x = 4
| : (– 2)
x = –2
Die Lösung lautet also x = – 2 und y = – 9.
Man kann auch mit der Einsetzprobe argumentieren:
2 · (– 2) – 3 · 9 = 23
| zusammenfassen
– 31 = 23 (falsch)
Also kann x = – 2 und y = 9 keine Lösung sein.
Teste dich selbst – Lösungen
251
b) richtig – Bei der Lösung dieses Problems muss man die
geometrische und die algebraische Darstellung von Geraden
betrachten und so argumentieren: Hat man ein LGS mit zwei
Unbekannten und zwei Gleichungen, so lassen sich die Gleichungen als Geraden darstellen und ihr Schnittpunkt ist die
Lösung des LGS. Bei einer unterschiedlichen Steigung sind
die beiden Geraden nicht parallel, sie haben also genau einen Schnittpunkt. Damit hat das zugehörige LGS genau eine
Lösung.
c) richtig – Zur Lösung dieses Problems wählt man am besten das Einsetzungsverfahren: Mit dem Auflösen von II nach
x erhält man:
I: 2 y = 6 – 5 x
IIa: x = 4,5 – 1,5 y
Das Einsetzen von IIa in I liefert:
2 y = 6 – 5 (4,5 – 1,5 y) | Klammer auflösen
2 y = 6 – 22,5 + 7,5 y
| zusammenfassen
2 y = – 16,5 + 7,5 y
| – 7,5 y
– 5,5 y = – 16,5
| : (– 5,5)
y=3
Das Einsetzen von y = 3 in II liefert:
2x = 9 – 3·3
| zusammenfassen
2x = 0
|:2
x=0
Die Lösung lautet x = 0 und y = 3, damit gilt: x + y = 3.
d) richtig – Man kann dieses Problem lösen, indem man
zeigt, dass die Gleichungen die dargestellten Geraden beschreiben. Löst man die Gleichungen I und II nach y auf,
erhält man zwei Geradengleichungen:
I: y = 0,3 – 0,7 x; m = – 0,7 und n = 0,3
II: y = 0,6 – 0,4 x; m = – 0,4 und n = 0,6
Mithilfe des Gleichsetzungsverfahrens erhält man den
Schnittpunkt der Geraden bzw. die Lösung des LGS:
I = II: 0,3 – 0,7 x = 0,6 – 0,4 x | + 0,4 x
0,3 – 0,3 x = 0,6
| – 0,3
– 0,3 x = 0,3
| : (– 0,3)
x = –1
Das Einsetzen von x = – 1 in I liefert: y = 0,3 + 0,7 = 1.
Aus Fig. 1 kann man neben dem Schnittpunkt (– 1 | 1) der
Geraden jeweils für jede Gerade zwei Punkte ablesen und
daraus die Steigung berechnen:
Gerade 1:
– 2,5 – 1
7
P1 (– 1 | 1) und P2 (4 |– 2,5); m = _
= –_
10
4 – (– 1)
Gerade 2:
–1 – 1
4
Q1 (– 1 | 1) und Q2 (4 | – 1); m = _
= –_
10
4 – (– 1)
Nun argumentiert man: Da die in Fig. 1 und die durch die
Gleichungen I und II dargestellten Geraden dieselbe Steigung und denselben Schnittpunkt besitzen, ist Fig. 1 eine
Darstellung des LGS mit den Gleichungen I und II.
e) falsch – Bei der Lösung dieses Problems kann man
geschickt argumentieren, indem man die geometrische
Darstellung eines LGS betrachtet und zur algebraischen in
Beziehung setzt: Ein LGS mit zwei Gleichungen und zwei
Unbekannten lässt sich in einem Koordinatensystem durch
252
Teste dich selbst – Lösungen
zwei Geraden darstellen, wobei die gemeinsamen Punkte
der Geraden Lösungen des LGS sind. Zwei Geraden können
sich entweder in einem Punkt schneiden (genau eine Lösung
– im LGS: „x = a; y = b“), sie können identisch sein (unendlich viele Lösungen – im LGS: allgemeine wahre Aussage,
z. B. „0 = 0“), sie können aber auch parallel zueinander liegen
(keine Lösung – im LGS: allgemeine falsche Aussage, z. B.
„0 = 5“).
f) richtig – Hier kann man geschickt mit der geometrischen
Darstellung eines LGS argumentieren: Bei I und II handelt
es sich um zwei Geraden, die beide durch den Punkt (0 | – 5)
verlaufen (n = – 5) und nur diesen Punkt als Schnittpunkt
besitzen, da sie verschiedene Steigungen haben. Damit ist
(0 | – 5) die einzige Lösung des LGS.
g) falsch – Hier argumentiert man so: Es ist zwar richtig,
dass sich drei Geraden zweimal schneiden können; Lösung
des zugehörigen LGS kann jedoch nur ein Punkt sein, in dem
sich alle drei Geraden schneiden, da alle drei durch die (Geraden-)Gleichungen dargestellten Beziehungen für x und y
(gleichzeitig!) erfüllt sein müssen.
4 Zahlenbereiche
a) falsch – Hier argumentiert man mit einem Gegenbeispiel:
Periodische Dezimalzahlen besitzen unendlich viele Nachkommastellen, lassen sich jedoch als Bruch darstellen und
sind daher rational, z. B.: _31 = 0,333 333 333 …
b) richtig – Man argumentiert: Wenn der Nenner ein Teiler
des Zählers ist, dann ist der Zähler ein Vielfaches des Nenners und der Bruch lässt sich vollständig kürzen; man erhält
999 _
3 · 333
eine ganze Zahl, z. B.: _
= 333.
3 =
3
c) richtig – Hier argumentiert man mit Rechenregeln: Wegen
der Regel „Minus mal Minus ergibt Plus“ ist das Produkt
einer geraden Anzahl negativer Zahlen immer positiv; damit
ist das Produkt einer ungeraden Anzahl (z. B. 789) negativer
Zahlen stets negativ, denn „Minus mal Plus ergibt Minus“.
d) richtig – Hier muss man in mehreren Schritten argumentieren: Bei einem echten Bruch ist der Zähler kleiner als
der Nenner, der Wert des Bruches ist also kleiner als 1. Das
Produkt zweier Zahlen, die kleiner sind als 1, ist in jedem Fall
wieder kleiner als 1. Dadurch bleibt der Zähler, auch wenn
man kürzen kann, stets kleiner als der Nenner. Das Ergebnis
ist also ein echter Bruch.
__
e)__falsch – __Man argumentiert mit einem Gegenbeispiel: √2 ,
√__
3 , und
irrational, ___
__ √ 6__sind ______
√ 2 · √ 3 · √ 6 = √ 2 · 3 · 6 = √ 36 = 6 jedoch rational.
Funktionen
5 Prozent- und Zinsrechnung
5
a) richtig – _8 = 0,625 = 62,5 % (0,01 = 1 %).
b) richtig – G = 12 700; p = 7 %. Damit gilt:
W = p · G = 7 % · 12 700 = 0,07 · 12 700 = 889.
c) falsch – W = 49,00; p = 100 % – 30 % = 70 %. Damit gilt:
49
49
10
W _
_
G=_
p = 70 % = _
0,7 = 49 · 7 = 70. Die Hose hat also zuvor
70 Euro und nicht 69 Euro gekostet.
d) falsch – W = 84,49; p = 100 % + 19 % = 119 %. Damit gilt:
84,49 84,49
W _
G=_
p = 119 % = _
1,19 = 71. Der MP3-Player kostet ohne Mehrwertsteuer 71,00 Euro, nicht 68,44 Euro.
e) falsch – G = 4500; p = 3 %; t = 4 · 30 = 120. Man berechnet zunächst die Jahreszinsen W:
W = p · G = 3 % · 4500 = 0,03 · 4500 = 135. Für 4 Monate
120
1
_
erhält man 135 · _
360 = 135 · 3 = 45 Euro Zinsen. Damit erhält
man 4500 Euro + 45 Euro = 4545 Euro ausbezahlt.
f) falsch – G = x; pA = 2 %; pB = 4 %; t = 10;
Bank A: Kapital: KA = (1 + pA)t · G = 1,0210 · x ≈ 1,219 x
Zinsen: KA – G = 1,219 x – x = 0,219 x
Bank B: Kapital: KB = (1 + pB)t · G = 1,0410 · x ≈ 1,480 x
Zinsen: KB – G = 1,480 x – x = 0,480 x
0,480 x : 0,219 x ≈ 2,2 > 2
Bei der Bank B erhält man wegen des Zinseszinseffekts
mehr als doppelt so viele Zinsen wie bei der Bank A.
6 Zuordnungen
a) richtig – Man ordnet der Situation zunächst das richtige
mathematische Modell zu: Die Zuordnung Liter (= Anzahl der
Milchtüten) ¥ Preis ist proportional, man kann daher mit folgendem Dreisatz rechnen:
3 Liter
1,77 Euro
:3
:3
1 Liter
0,59 Euro
·5
·5
5 Liter
2,95 Euro
Fünf Liter Milch kosten also 2,95 Euro.
b) falsch – Hier argumentiert man mithilfe folgender Plausibilitätsüberlegung: Da die Dauer des Stücks nicht von der
Anzahl der Musiker abhängt, handelt es sich nicht um eine
antiproportionale Zuordnung, der Dreisatz kann hier also
nicht angewendet werden.
c) falsch – Man ordnet der Situation zunächst das richtige
mathematische Modell zu: Die Zuordnung Anzahl der Pferde
¥ Anzahl der Tage ist antiproportional, es kann daher mit
folgendem Dreisatz gerechnet werden:
12 Pferde
6 Tage
: 12
· 12
1 Pferd
72 Tage
·8
:8
8 Pferde
9 Tage
Für 8 Pferde reicht der Vorrat also nur 9, nicht 10 Tage.
d) falsch – Man argumentiert: Ein dickeres Buch kostet zwar
in der Regel mehr. Damit die Zuordnung proportional ist,
müsste jedoch immer gelten, dass ein Buch mit doppelter,
dreifacher etc. Dicke auch den doppelten, dreifachen etc.
Preis kostet. Dies ist nicht der Fall.
e) falsch – Man argumentiert: Der Graph einer proportionalen Zuordnung verläuft stets durch den Ursprung, hat also
den Achsenabschnitt n = 0. Eine beliebige Gerade mit n ≠ 0
ist also kein Graph einer proportionalen Zuordnung. Es gilt
allerdings die Umkehrung, dass jeder Graph einer proportionalen Zuordnung eine Gerade ist, nämlich eine Gerade mit
der speziellen Gleichung y = m x (da n = 0).
f) falsch – Die Gleichung y = _3x = _31 x gehört zu einer propory
tionalen Zuordnung der Form y = m x, der Quotient _x hat
1
den konstanten Wert _3 . Der zugehörige Graph ist eine durch
den Ursprung verlaufende Gerade mit der Steigung _31 . Die
Gerade in Fig. 1 hat die Steigung 3 und ist daher nicht der
Graph der genannten Zuordnung.
7 Geraden
a) falsch – Der Punkt (4 | 3) liegt dann auf der Geraden, wenn
die Gleichung y = 3 x – 5 für x = 4 und y = 3 erfüllt ist.
Durch Einsetzen erhält man: 3 = 3 · 4 – 5 = 7 (falsch).
Der Punkt (4 | 3) liegt also nicht auf der Geraden.
b) falsch – Die Gleichung y = 0,6 x + 1 beschreibt eine Gerade mit der positiven Steigung m = 0,6 und dem Achsenabschnitt n = 1. Die Gerade in Fig. 2 hat zwar ebenfalls den
Achsenabschnitt 1, die Steigung ist jedoch negativ. Die Gerade in Fig. 2 besitzt die Gleichung y = – 0,6 x + 1
(m = – 0,6 lässt sich aus den Punkten (– 2,5 | 2,5) und (0 | 1)
berechnen).
c) falsch – Die Steigung der Geraden lässt sich aus den
– 5 – (– 1) – 4
_
beiden Punkten berechnen: m = _
2 – 3 = – 1 = 4. Den Achsenabschnitt n erhält man durch Einsetzen z. B. des Punktes
(3 | – 1) in die Gleichung y = 4 x + n:
– 1 = 4 · 3 + n | – 12
– 13 = n
Die Geradengleichung lautet also y = 4 x – 13.
d) richtig – Man argumentiert: Die Gleichung x = 3 besagt,
dass für alle Werte von y der x-Wert konstant 3 ist. Die Gerade besteht also aus den Punkten (3 | y) für alle y. Diese Punkte liegen auf einer Geraden, die parallel zur y-Achse (mit der
Gleichung x = 0) liegt.
e) richtig – Zur Lösung dieses Problems muss man die relevanten geometrischen Eigenschaften der Gleichungen ermitteln: Die Gerade mit y = 3 x + 5 hat die Steigung m = 3,
die Gerade mit y = 2 x + 7 hat die Steigung m = 2. Während
die zweite Gerade je Einheit nach rechts um 2 Einheiten ansteigt, steigt die erste Gerade um 3 Einheiten an, sie verläuft
also steiler.
f) falsch – Man argumentiert mit einem Gegenbeispiel: Die
konstanten Funktionen der Form y = a (a konstant und
a ≠ 0, z. B. y = 1) schneiden die x-Achse gar nicht, die konstante Funktion y = 0 hat mit der x-Achse unendlich viele
gemeinsame Punkte. Richtig ist jedoch, dass jede lineare
Funktion genau einmal die y-Achse schneidet, und zwar in
dem Punkt (0 | n) mit dem Achsenabschnitt n.
Teste dich selbst – Lösungen
253
g) falsch – Hier kann man geometrisch argumentieren: Die
Geraden g und h besitzen dieselbe Steigung m = 4, sie verlaufen also parallel; da sie einen unterschiedlichen Achsenabschnitt n haben, sind sie nicht identisch, sondern liegen
wirklich parallel zueinander. Weil sich parallele Geraden nicht
schneiden, können sie in S (4 | – 1) auch keinen Schnittpunkt
haben.
G
c
E
c
C
c
b
a
A
B
D
Fig. 1
F
Geometrie
8 Winkelbeziehungen
a) richtig – Man argumentiert so: Da sich Nebenwinkel zu
180° ergänzen, müssen von je zwei nebeneinander liegenden
Winkeln beide 90° betragen. Damit schneiden sich die Geraden im rechten Winkel.
b) richtig – Man kann so argumentieren: Im Parallelogramm
gilt: Die Innenwinkelsumme beträgt 360° (gilt für alle Vierecke) und die gegenüberliegenden Winkel sind gleich groß
(Wechselwinkel). Wenn man zwei Winkel an benachbarten
Eckpunkten kennt, sind dies zugleich die Größen der jeweils
gegenüberliegenden anderen Winkel; kennt man zwei (dann
gleich große) gegenüberliegende Winkel, dann sind die beiden anderen Winkel gleich und so groß, dass sie sich jeweils
mit einem der bekannten Winkel zu 180° ergänzen. In einem
Parallelogramm wäre es sogar ausreichend, nur einen einzigen Winkel zu kennen.
c) falsch – Bei dieser Argumentation muss man die Begriffe
„Viereck“ und „Rechteck“ richtig einordnen. Da die Innenwinkelsumme in einem Viereck 360° beträgt, muss bei drei
rechten Winkeln auch der vierte Winkel 90° betragen. Ein
Viereck mit vier rechten Winkeln nennt man ein Rechteck (im
Spezialfall ein Quadrat).
d) richtig – Die gegebene Situation muss in einen Term (ein
mathematisches Modell) übersetzt werden.
Für a und seinen Nebenwinkel b gilt:
I:
a + b = 180°
II:
a = 4 b (a ist viermal so groß wie b)
Das Einsetzen von II in I liefert:
4 b + b = 180°
| zusammenfassen
5 b = 180°
|:5
b = 36°
Der Nebenwinkel b ist also 36° groß.
9 Dreiecke
a) richtig – Da die Summe der Innenwinkel im Dreieck 180°
beträgt, gilt für den gesuchten Winkel c bei gegebenen Winkeln a und b: c = 180° – a – b.
b) falsch – Man kann mit einem Gegenbeispiel argumentieren: Dreiecke mit den gleichen Winkeln a, b und c sind nicht
kongruent, sondern nur ähnlich. Man findet daher beliebig
viele Dreiecke mit jeweils gleichen Winkeln (z. B. die Dreiecke
ABC, ADE und AFG in Fig. 1).
254
Teste dich selbst – Lösungen
c) richtig – Man kann mit einem geometrischen Satz argumentieren: Mit den Seiten a und b sowie dem Winkel c
sind zwei Seiten und der von diesen eingeschlossene Winkel
gegeben. Nach dem Kongruenzsatz (sws) sind deshalb alle
Dreiecke mit denselben Werten für a, b und c zu einander
kongruent und damit ist die Konstruktion eines solchen Dreiecks eindeutig.
d) falsch – Man kann argumentieren: Grundsätzlich lässt
sich zwar nach dem Kongruenzsatz (sss) ein Dreieck mit drei
gegebenen Seiten eindeutig zeichnen, allerdings nur dann,
wenn die Summe zweier Seitenlängen stets größer ist als die
dritte – andernfalls entsteht kein Dreieck. Da die Summe von
a und b (a + b = 12) kleiner ist als c (c = 13), lässt sich kein
Dreieck konstruieren.
e) richtig – In einem gleichseitigen Dreieck sind alle Seiten
gleich lang und alle Winkel gleich groß. Da die Innenwinkelsumme im Dreieck 180° beträgt, sind alle Winkel 60° groß, es
kann keinen rechten Winkel geben.
f) falsch – Mithilfe der Problemlösestrategie, Hilfsfiguren
zu verwenden, kann man ein Gegenbeispiel finden und so
argumentieren: Der Schnittpunkt der Mittelsenkrechten ist
der Mittelpunkt des Umkreises des Dreiecks. Wählt man auf
einem Kreis nun drei Punkte, die alle auf derselben Seite
eines eingezeichneten Durchmessers liegen, erhält man ein
Dreieck, dessen Schnittpunkt der Mittelsenkrechten (dies ist
der Kreismittelpunkt) außerhalb des Dreiecks liegt (vgl. Fig. 2)
C
A
B
M
Fig. 2
g) richtig – Bei der Argumentation hilft der Satz des Thales:
Der der längsten Seite des Dreiecks gegenüberliegende
Punkt liegt auf dem Thaleskreis, sodass der Winkel bei diesem Punkt 90° beträgt. Hat man einen an die längste Seite
des Dreiecks angrenzenden Winkel gegeben, muss man nur
den zweiten angrenzenden Winkel berechnen, der sich nach
der Innenwinkelsumme im Dreieck mit dem ersten zu 90°
ergänzen muss.
10 Vierecke
a) falsch – Es hilft die Problemlösestrategie des Auspro__
bierens: Man zeichnet zunächst die Strecke BC mit der
Länge b = 5 cm ein und kann an C den Winkel c = 65° abtragen. Der Eckpunkt A ist der Schnittpunkt des Kreises um
B mit dem Radius 3 cm (wegen a = 3 cm) und einer Geraden,
die die Gerade CD im Winkel d = 100° schneidet. Da es viele
solcher Geraden CD gibt, die sich mit dem Kreis schneiden
(zumeist in zwei Punkten), ist das Viereck nicht eindeutig
konstruierbar (vgl. Fig. 1).
A’2
A2
A1
a2
a1
d
A’1
a’2
D2
d
D1
a’1
B
c = 65°
b
C
Fig. 1
b) richtig – Das Problem der Konstruktion lässt sich lösen,
indem man die Beziehung der gegebenen Größen im Trapez
beachtet. Da c im Abstand der Höhe ha parallel zu a liegt und
wegen der Gleichschenkligkeit die Mittelsenkrechte von a die
Symmetrieachse ist, ist die Konstruktion eindeutig (s. Fig. 2):
Man zeichnet die Strecke a mit den Eckpunkten A und B
und ihre Mittelsenkrechte ein, die a im Punkt E schneidet.
Die Höhe ha trägt man von E aus auf der Mittelsenkrechten
ab und erhält den Punkt F. Man kann nun von F aus auf der
Parallelen zur Seite a zu beiden Seiten die Hälfte der Strecke
c abtragen und erhält die beiden Eckpunkte C und D.
C
F
C
B
D
d
a
A
D
ha
a
A
a
E
Fig. 3
11 Flächeninhalte
a) falsch – Da der rechte Winkel an die beiden kürzeren Seiten des Dreiecks angrenzt, kann b als Grundseite und a als
Höhe des Dreiecks angesehen werden. Damit gilt:
A = _21 · Grundseite · Höhe = _21 · b · a = _21 · 5 cm · 3 cm = 7,5 cm2.
b) falsch – AQuadrat = a · a = 5 cm · 5 cm = 25 cm2
ATrapez = _21 · (a + c) · ha = _21 · (7 cm + 3 cm) · 5 cm = 25 cm2. Die
Flächeninhalte sind also gleich.
c) falsch – Mithilfe der Problemlösestrategie, eine geeignete
Hilfsfigur zu zeichnen (Fig. 4), kann man argumentieren:
Wenn ein Parallelogramm mit der Grundseite a = 2 cm den
Flächeninhalt 10 cm2 haben soll, muss wegen der Flächenformel A = Grundseite · Höhe die Höhe des Parallelogramms
5 cm betragen. Da aber die Seite b bereits 5 cm lang ist,
muss die Höhe ha in jedem Fall kleiner sein als b und damit
kleiner als 5 cm (vgl. Fig. 4). Damit ist auch die Fläche kleiner
als 10 cm2.
b
a
b
c
B
Fig. 2
c) richtig – Bei dieser Argumentation muss man die Begriffe
(Ober- und Unterbegriff) richtig einordnen. Ein Viereck ist ein
Trapez, wenn zwei gegenüberliegende Seiten parallel zueinander sind. Da dies beim Rechteck auch der Fall ist, ist das
Rechteck ein Trapez.
d) falsch – Bei dieser Argumentation muss man die Begriffe
richtig einordnen. Bei einem Parallelogramm sind, wie bei
einer Raute, die gegenüberliegenden Seiten parallel, sie müssen jedoch nicht gleich lang sein. Man wählt als Gegenbeispiel ein Parallelogramm, bei dem die Seiten a und b unterschiedlich lang sind. Dieses Parallelogramm ist keine Raute.
e) falsch – Man argumentiert mit einem Gegenbeispiel: Da
bei einem Drachen die Strecken a und d bzw. b und c gleich
lang sind, ist der Drachen achsensymmetrisch mit der Symmetrieachse AC (Fig. 3). Ein Drachen ist jedoch kein Trapez,
da er keine parallelen Seiten haben muss.
Fig. 4
d) falsch – Man argumentiert mit einem Gegenbeispiel:
Ein Quadrat mit Seitenlänge 2 cm hat den Flächeninhalt
A = 2 cm · 2 cm = 4 cm2; eine Raute hat den Flächeninhalt
A = Grundseite · Höhe. Bei gleicher Seitenlänge beträgt die
Grundseite ebenfalls 2 cm, die Höhe jedoch ist analog zur Begründung aus c) (vgl. Fig. 4) kleiner als 2 cm. Damit ist auch
der Flächeninhalt kleiner als 4 cm2.
e) richtig – Der Flächeninhalt eines Kreises beträgt A = p · r2.
Ein Kreis mit dem Radius r = 3 cm hat also den Flächeninhalt A = p · r2 = p · (3 cm)2 = p · 9 cm2 ≈ 28,3 cm2.
f) falsch – Der Flächeninhalt eines Kreises mit dem Radius r
beträgt Aklein = p · r2 und der eines Kreises mit dem Radius
2 r beträgt Agroß = p · (2 r)2 = p · 4 r2 = 4 · Aklein.
Damit vervierfacht sich der Flächeninhalt.
Teste dich selbst – Lösungen
255
12 Körper
a) falsch – Die Einheiten sind nicht korrekt. Das Prisma besitzt das Volumen V = Grundfläche · Höhe = 12 cm2 · 3 cm =
36 cm3 und nicht 36 m3.
b) richtig – Man argumentiert so: Ein Prisma ist ein Körper
mit zwei zueinander parallelen Flächen, den sogenannten
Grundflächen, und Rechtecken als Seitenflächen. Da die
Dreiecksflächen der Verpackung zueinander parallel liegen
und die Seitenflächen rechteckig sind, handelt es sich um ein
Prisma.
c) falsch – Ein Zylinder hat das Volumen V = Grundfläche · Höhe = p r2 · h. Schon ein Überschlagen (Problemlösestrategie) des Volumens zeigt, dass der Wert 137,1 cm3 zu
klein ist: V ≈ 3 · 52 · 2 = 150. Eine genauere Rechnung bestätigt dies: V = p · 52 · 2 = 50 p ≈ 157,1 cm3.
d) richtig – Ein Würfel mit Seitenlänge a hat das Volumen
Vklein = a3, ein Würfel mit der doppelten Seitenlänge 2 a hat
das Volumen Vgroß = (2 a)3 = 23 · a3 = 8 · a3 = 8 · Vklein .
e) richtig – Eine 1-Liter-Packung hat ein Volumen von 1 dm3
= 1000 cm3. Ein Würfel mit dem Volumen V = a3 = 1000 cm3
3 _____
3_
hat die Seitenlänge a = 9V = 91000 cm3 = 10 cm.
f) richtig – Mithilfe der Problemlösestrategie, ein geeignetes
Beispiel zu finden (hier ein Prisma mit minimaler Flächenanzahl), kann man so argumentieren: Ein Prisma besitzt zwei
zueinander parallele Grundflächen, die, damit sie ein Vieleck
darstellen, mindestens 3 Eckpunkte haben müssen. Daraus
folgt, dass zu einem Prisma mindestens 3 Seitenflächen (die
an das Dreieck der Grundfläche angrenzen) gehören, dass es
also insgesamt mindestens 5 Flächen besitzt.
Daten und Zufall
13 Wahrscheinlichkeiten
a) richtig – Das Ereignis „Würfeln einer geraden Zahl“ umfasst die drei Ergebnisse „2“, „4“ und „6“. Da es sich um ein
Laplace-Experiment handelt, haben alle drei Ergebnisse die
Wahrscheinlichkeit _61 . Nach der Summenregel beträgt die
Wahrscheinlichkeit für das Ereignis „Würfeln einer geraden
Zahl“ p = 3 · _61 = 0,5.
b) richtig – Wenn man die Problemlösestrategie anwendet, die Beziehungen der Flächen und Zahlen zueinander
zu untersuchen, kommt man zu folgender Argumentation:
Die drei verschieden großen Flächen liegen beim Würfeln
sicherlich mit unterschiedlich großen Wahrscheinlichkeiten
oben; da jedoch die Summe der Zahlen auf den gegenüber
liegenden Flächen stets 7 beträgt und die 7 sich aus einer
geraden und einer ungeraden Zahl zusammensetzt, verteilen
sich jeweils die drei geraden und die drei ungeraden Zahlen
auf diese drei Flächen. Da man für gleich große Flächen außerdem gleich große Wahrscheinlichkeiten annehmen sollte,
beträgt die Summe der Wahrscheinlichkeiten für die drei
verschieden großen Flächen und damit für das Ereignis „Würfeln einer geraden Zahl“ 0,5.
c) falsch – Die Wahrscheinlichkeit für „Wappen“ und „Zahl“
256
Teste dich selbst – Lösungen
beträgt je 0,5. Nach der Pfadregel gilt für die Wahrscheinlichkeit „zweimal Zahl“ p = _21 · _21 = _41 = 0,25.
Das Ereignis „einmal Zahl und einmal Wappen“ setzt sich zusammen aus den Ergebnissen „erst Zahl, dann Wappen“ und
„erst Wappen, dann Zahl“. Aus der Pfadregel und der Summenregel erhält man p = 2 · _21 · _21 = _24 = 0,5. Die Wahrscheinlichkeiten sind also unterschiedlich groß.
d) falsch – Das Ereignis „eine Zahl kleiner als 3 würfeln“ enthält die Ergebnisse „1“ und „2“; das Gegenereignis umfasst
alle übrigen Ergebnisse „3“, „4“, „5“ und „6“ und könnte daher
z. B. lauten „eine Zahl größer als 2 würfeln“; das Ereignis
„eine Zahl größer als 3 würfeln“ schließt die 3 aus und ist
daher nicht das Gegenereignis.
e) falsch – Man muss zwischen der Realität und dem mathematischen Modell unterscheiden: Relative Häufigkeiten sind
„reale“ in Zufallsexperimenten ermittelte Werte, die beschreiben, wie häufig ein bestimmtes Ergebnis in einem Experiment bezogen auf die Gesamtzahl der Versuche aufgetreten
ist, z. B.: Es trat bei 50 Münzwürfen 28-mal „Wappen“ auf, die
28
relative Häufigkeit für „Wappen“ beträgt _
50 = 0,56 = 56 %.
Wahrscheinlichkeiten hingegen sind „theoretische Größen“ eines mathematischen Modells, mit denen man
versucht, relative Häufigkeiten bei Zufallsexperimenten
vorherzusagen, z. B.: Die Wahrscheinlichkeit für „Wappen“
beträgt 50 % bedeutet, man erwartet bei 1000 Münzwürfen
etwa 1000 · 50 % = 500 „Wappen“.
f) falsch – Zum Ereignis „dreimal hintereinander eine 5 würfeln“ gehört nur das Ergebnis „5, 5, 5“ mit der Wahrschein3
lichkeit p = 2 _61 3 ≈ 0,46 % . Zum Ereignis „in drei Würfen die
Summe 15 würfeln“ hingegen gehören die Ergebnisse „5, 5,
5“, „6, 4, 5“, „4, 6, 5“, „4, 5, 6“, „6, 5, 4“, „5, 4, 6“, „5, 6, 4“, „6, 6, 3“,
„6, 3, 6“ und „3, 6, 6“. Damit ergibt sich die Wahrscheinlichkeit
3
p = 10 · 2 _61 3 ≈ 4,6 %. Die Wahrscheinlichkeiten sind also unterschiedlich groß.
14 Statistik
a) falsch – Man erstellt zunächst eine geordnete Liste: 2, 2,
3, 4, 5, 5, 6, 7, 8. Der Median der Liste mit 9 Werten ist der
mittlere, also der 5. Wert, er ist 5 und nicht 4.
b) falsch – Das arithmetische Mittel beträgt
1
42
_ · (2 + 8 + 5 + 3 + 2 + 6 + 7 + 4 + 5) = _ ≈ 4,7.
9
9
Anzahl der Treffer
34
_
c) falsch – p = __
Gesamtzahl der Würfe = 200 = 0,17 = 17 %.
d) richtig – Mithilfe der Problemlösestrategie, den allgemeinen Fall „Alle Werte betragen a“ zu betrachten, kann man
argumentieren: Der Mittelwert ist die Summe aller Werte
geteilt durch die Anzahl der Werte; bei n gleichen Werten a
gilt damit für den Mittelwert: _n1 · (n · a) = a.
e) richtig – Bei der Argumentation hilft die Problemlösestrategie, konkrete Werte zu betrachten; dabei zeigt sich,
dass das mathematische Modell der Kenngrößen „Median
und arithmetisches Mittel“ hier nicht angemessen ist: Bei
einer Bundestagswahl sehen die Ergebnisse so aus, dass
für die einzelnen Parteien angegeben wird, wie viel Prozent
der Wählerstimmen sie erhalten haben, man erhält einzelne
Zuordnungen (z. B. CDU ¥ 39,4 %; SPD ¥ 37,3 %; …). Um den
Median bestimmen oder das arithmetische Mittel berechnen
zu können, benötigt man jedoch eine Datenreihe mit (einheitlichen) Zahlenwerten.
f) richtig – Für das arithmetische Mittel aus den 5 Daten x1,
x2, x3, x4 und x5 gilt:
1
_ · (x + x + x + x + x ) = 3
| ·5
1
2
3
4
5
5
x1 + x2 + x3 + x4 + x5 = 15
Die Summe aller Daten muss also 15 sein.
15 Diagramme
In den folgenden Aufgaben muss das mathematische Modell der Diagrammform „Boxplot“ angemessen interpretiert
werden.
a) richtig – Das (zeitliche) Maximum bei den Mädchen liegt
oberhalb des Maximums bei den Jungen, das langsamste
Mädchen benötigt also insgesamt die längste Zeit und ist
damit langsamer als jeder Junge.
b) richtig – Die Box der Jungen umfasst die Zeiten zwischen
8,6 s und 9,5 s. Da in der Box eines Boxplots ca. die Hälfte
aller Daten liegen, laufen 50 % der Jungen zwischen 8,6 s und
9,5 s.
c) richtig – Bei den Mädchen umfasst die Box die Zeiten
zwischen ca. 8,9 s und 9,5 s. Da in dieser Box bereits 50 % der
Daten liegen, sind also mindestens 50 % der Mädchen 8,6 s
und 9,5 s gelaufen. Dass es mehr als 50 % sind, kann nicht
sicher gesagt werden, da sich aus dem Boxplot nicht ablesen
lässt, ob zwischen 8,6 s und 8,9 s auch ein Datenwert liegt.
d) richtig – Da das Minimum der Mädchen unterhalb dem
der Jungen liegt, ist ein Mädchen die beste Zeit gelaufen.
e) richtig – Das Maximum bei den Jungen liegt oberhalb von
10 s, damit ist der langsamste Junge über 10 s gelaufen.
f) richtig – Da zwischen dem Minimum und dem unteren
Quartil (bei ca. 8,6 s) immer ca. 25 % aller Daten liegen, sind
ca. 25 % der Jungen 8,6 s und schneller gelaufen.
Teste dich selbst – Lösungen
257