13. Ubungsblatt zur Experimentalphysik II


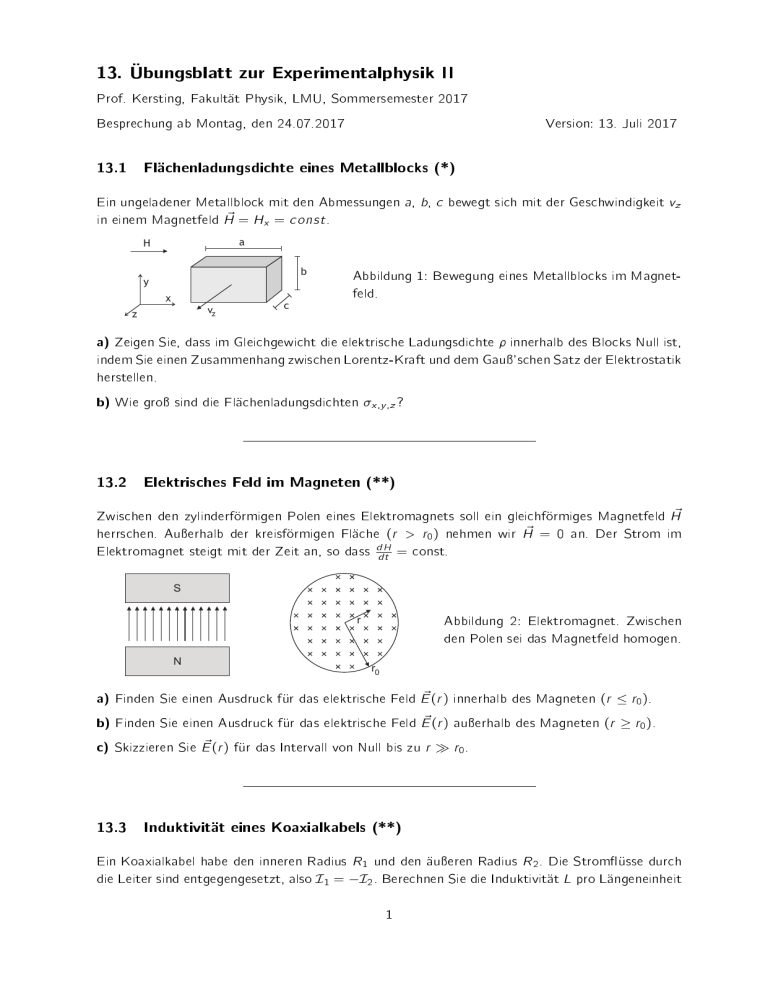
13. Ubungsblatt
zur Experimentalphysik II
Prof. Kersting, Fakultat Physik, LMU, Sommersemester 2017
Besprechung ab Montag, den 24.07.2017
13.1
Version: 13. Juli 2017
Fl
achenladungsdichte eines Metallblocks (*)
Ein ungeladener Metallblock mit den Abmessungen a, b, c bewegt sich mit der Geschwindigkeit v
in einem Magnetfeld H~ = H = c onst .
z
x
a
H
b
y
x
vz
z
c
Abbildung 1: Bewegung eines Metallblocks im Magnetfeld.
Zeigen Sie, dass im Gleichgewicht die elektrische Ladungsdichte innerhalb des Blocks Null ist,
indem Sie einen Zusammenhang zwischen Lorentz-Kraft und dem Gau'schen Satz der Elektrostatik
herstellen.
a)
b)
Wie gro sind die Flachenladungsdichten 13.2
x ;y ;z
?
Elektrisches Feld im Magneten (**)
Zwischen den zylinderformigen Polen eines Elektromagnets soll ein gleichformiges Magnetfeld H~
herrschen. Auerhalb der kreisformigen Flache (r > r0 ) nehmen wir H~ = 0 an. Der Strom im
Elektromagnet steigt mit der Zeit an, so dass
= const.
dH
dt
S
Abbildung 2: Elektromagnet. Zwischen
den Polen sei das Magnetfeld homogen.
r
N
r0
r0).
b) Finden Sie einen Ausdruck f
ur das elektrische Feld E~ (r ) auerhalb des Magneten (r r0 ).
~ (r ) f
c) Skizzieren Sie E
ur das Intervall von Null bis zu r r0 .
a)
Finden Sie einen Ausdruck fur das elektrische Feld E~ (r ) innerhalb des Magneten (r
13.3
Induktivit
at eines Koaxialkabels (**)
Ein Koaxialkabel habe den inneren Radius R1 und den aueren Radius R2 . Die Stromusse durch
die Leiter sind entgegengesetzt, also I1 = I2 . Berechnen Sie die Induktivitat L pro Langeneinheit
1
. Vernachlassigen Sie die Magnetfelder innerhalb der metallischen Leiter. Hilfreich ist eine innitesimale Flache, gegeben durch d r und .
L
2R2
I1
R1
dr
Abbildung 3: Koaxialkabel.
2R1
I2
r
R2
13.4
Beschleunigter Schlitten (*)
Ein leitender Schlitten mit elektrischem Widerstand R bende sich auf zwei Schienen, welche den
Abstand b haben und vom Strom I durchossen werden. Das Magnetfeld in der Umgebung der
Schienen soll als homogen angenommen werden. Der Stromuss durch den Schlitten beschleunigt
ihn nach rechts (Abb. 4).
bat
Welche Maximalgeschwindigkeit erreicht der Schlitten, wenn nur sein elektrischer Widerstand R
berucksichtigt wird, aber Reibungswiderstande und elektrische Widerstande der Schienen vernachlassigt werden?
Ubat
B
R
b
Ibat
13.5
Abbildung 4: Schlitten auf stromdurchossenen Schienen.
Geschlossene Leiterschleife (*)
Eine geschlossene Leiterschleife mit den Abmessungen a = 10 cm und b = 20 cm bende sich in
einem homogenen Magnetfeld von B = 2 T, welches parallel zur Flachennormalen der Leiterschleife
orientiert ist. Die Leiterschleife wird mit einer konstanten Geschwindigkeit von v = 2 in x Richtung bewegt und verlasst hierdurch den Feldbereich.
 nderung des magnetischen Flusses die induzierte Spannung U . Neha) Berechnen Sie aus der A
men Sie an, dass sich die Leiterschleife zum Zeitpunkt t = 0 gerade noch vollstandig im Magnetfeld
bendet.
cm
s
i nd
b) Geben Sie die technische Stromrichtung sowie deren Gr
oe an. Der Widerstand der Leiterschleife
sei R = 20 .
c) Welche Induktionsspannung Ui nd
wird?
liegt vor, wenn bei der Bewegung das Magnetfeld nicht verlassen
2
t=0
x
b
a
13.6
v
Verschiebestrom (*)
Ein Plattenkondensator habe den Radius R und einen Abstand d R. Der Kondensator wird mit
dem Strom I geladen. Zwischen den Platten wird das elektrische Feld als homogen angenommen.
Grundsatzlich gilt fur den Verschiebestrom:
I
D
= 0
d e l
(1)
dt
wobei der elektrische Fluss zwischen den Platten ist.
el
Abbildung 5: Schema zum Plattenkondensator,
nicht mastabsgetreu.
R
E
I
Zeigen Sie ausgehend von Gl. (1) uber die bekannten Zusammenhange aus der Elektrostatik zu
Flachenladungsdichte , Fluss und elektrischen Feld E , dass I = I gilt.
el
D
3