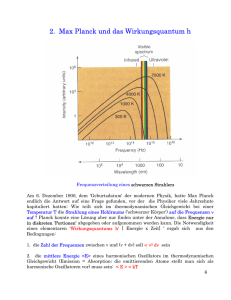
Thermodynamik und Statistik SS 1999

Thermodynamik und Statistik
SS 1999
W. Cassing
Institut fu
 r Theoretische Physik
Universit
at Giessen
1
Inhaltsverzeichnis
I Elementare Quantenmechanik der Vielteilchensysteme
1 Identische Teilchen
1.1
1.2
1.3
1.4
Konzept identischer Teilchen . . . . . .
Statistik . . . . . . . . . . . . . . . . .
Pauli-Prinzip fur N identische Teilchen
Zusammengesetzte Teilchen . . . . . .
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
. 8
. 10
. 11
. 12
Darstellung im Kongurationsraum . . . . . . . . . . . . . . . . .
Aufbau des Fock-Raumes . . . . . . . . . . . . . . . . . . . . . . .
Erzeugungs- und Vernichtungs-Operatoren . . . . . . . . . . . . .
Observable in der Teilchenzahl-Darstellung fur feste Teilchenzahl .
Anwendungsbeispiele . . . . . . . . . . . . . . . . . . . . . . . . .
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
3 Teilchenzahl-Darstellung fur Bosonen
3.1
3.2
3.3
3.4
3.5
Darstellung im Kongurationsraum . . . .
Fock-Raum fur Bosonen . . . . . . . . . .
Erzeugungs- und Vernichtungs-Operatoren
Observable . . . . . . . . . . . . . . . . . .
Anwendungsbeispiele . . . . . . . . . . . .
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
Energie des klassischen Strahlungsfeldes . . . .
Quantisierung . . . . . . . . . . . . . . . . . . .
Wechselwirkung von Strahlungsfeld und Materie
Die 0. Naherung . . . . . . . . . . . . . . . . . .
Absorption und Emission von Photonen . . . .
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
4 Quantisierung des Strahlungsfeldes: Photonen
4.1
4.2
4.3
4.4
4.5
8
.
.
.
.
2 Teilchenzahldarstellung fur Fermionen
2.1
2.2
2.3
2.4
2.5
7
II Grundlagen der statistischen Physik
5 Konzept der statistischen Gesamtheit
5.1
5.2
5.3
5.4
Mikro- und Makrozustande . . . .
Der statistische Operator . . . . .
Statistische Mittelwerte . . . . . .
Die klassische Dichtefunktion kl .
.
.
.
.
2
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
13
13
15
19
21
23
26
26
26
27
29
29
31
31
33
34
35
35
40
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
41
41
42
43
45
5.5 Zusammenfassung . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 48
6 Statistische Denition der Entropie
6.1
6.2
6.3
6.4
6.5
Entropie als Ma fur fehlende Information . . . . . . . . . . . . . . .
Ein einfaches Beispiel . . . . . . . . . . . . . . . . . . . . . . . . . . .
Zeitliche A nderung der Entropie . . . . . . . . . . . . . . . . . . . . .
Zeitumkehr-Invarianz: Mikro-Reversibilitat und Makro-Irreversibilitat
Die Postulate der statistischen Mechanik . . . . . . . . . . . . . . . .
7 Statistische Gesamtheiten im Gleichgewicht
7.1
7.2
7.3
7.4
7.5
7.6
Die uniforme Gesamtheit . . . . .
Die mikrokanonische Gesamtheit
Die kanonische Gesamtheit . . . .
Grokanonische Gesamtheit . . .
Der allgemeine Fall . . . . . . . .
Erganzungen . . . . . . . . . . .
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
Vorbemerkungen . . . . . . . . . . . . . . . . . . .
Mittlere Besetzungszahlen der Einteilchen-Zustande
Mittelwerte . . . . . . . . . . . . . . . . . . . . . .
Der klassische Grenzfall . . . . . . . . . . . . . . .
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
Einfuhrung . . . . . . . . . . . . . . . . . . . . . . . . . .
Fluktuationen . . . . . . . . . . . . . . . . . . . . . . . . .
Thermodynamische Storungstheorie . . . . . . . . . . . . .
Linear-Response . . . . . . . . . . . . . . . . . . . . . . . .
Beispiele . . . . . . . . . . . . . . . . . . . . . . . . . . . .
Fluktuations-Dissipations-Theorem . . . . . . . . . . . . .
Verallgemeinerung des klassischen Gleichverteilungssatzes .
Beispiele . . . . . . . . . . . . . . . . . . . . . . . . . . . .
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
Temperatur: Warmeaustausch . . . . . .
Chemisches Potential: Teilchenaustausch
Druck: Volumenaustausch, auere Arbeit
Einfache Beispiele . . . . . . . . . . . . .
Einstellung des Gleichgewichts . . . . . .
Thermodynamische Potentiale . . . . . .
Die Hauptsatze der Thermodynamik . .
Spezische Warme . . . . . . . . . . . .
Thermischer Ausdehnungskoezient . .
Das klassische ideale Gas . . . . . . . . .
10 Kleine Abweichungen vom Gleichgewicht
10.1
10.2
10.3
10.4
10.5
10.6
10.7
10.8
.
.
.
.
.
.
.
.
.
.
.
9 Statistische Mechanik und Thermodynamik
9.1
9.2
9.3
9.4
9.5
9.6
9.7
9.8
9.9
9.10
.
.
.
.
.
.
.
.
.
.
.
8 Unabhangige identische Teilchen
8.1
8.2
8.3
8.4
.
.
.
.
.
3
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
49
49
50
51
55
57
59
59
59
61
62
63
63
66
66
66
68
68
71
71
74
76
78
80
81
84
88
89
91
92
92
92
95
98
99
101
104
106
III Anwendungen der Statistischen Mechanik
107
11 Das ideale Fermi-Gas
108
11.1
11.2
11.3
11.4
11.5
11.6
Fermi-Verteilung . . . . . . . . . . . . . . . . . . . . . . . . .
Innere Energie und Teilchenzahl bei niedrigen Temperaturen T
Entartung des Fermi-Gases . . . . . . . . . . . . . . . . . . . .
Zustandsgleichung . . . . . . . . . . . . . . . . . . . . . . . . .
Schwankungen der mittleren Besetzungszahl . . . . . . . . . .
Gluhemission . . . . . . . . . . . . . . . . . . . . . . . . . . .
12 Das ideale Bose-Gas
12.1
12.2
12.3
12.4
12.5
12.6
12.7
Bose-Verteilung . . . . . . . . . . . . . . . .
Schwankungen der mittleren Besetzungszahl
Bose-Einstein-Kondensation . . . . . . . . .
Innere Energie und spezische Warme . . .
Photonen . . . . . . . . . . . . . . . . . . .
Detailed Balance . . . . . . . . . . . . . . .
Phononen in Festkorpern . . . . . . . . . . .
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
. . . . . . . 108
6= 0: . . . . 109
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
111
111
112
112
115
115
116
116
119
120
122
123
13 Magnetische und elektrische Eigenschaften der Materie
127
IV Nichtgleichgewichts - Dynamik
134
13.1
13.2
13.3
13.4
13.5
13.6
Denitionen . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
Theorem von Bohr - van Leeuwen . . . . . . . . . . . . . . . . . . . . . . .
Paramagnetismus . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
Klassische Theorie des Paramagnetismus und der Orientierungspolarisation
Magnetische Kuhlung . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
Negative Temperaturen . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
14 Kinetische Theorien fur Fermionen
14.1
14.2
14.3
14.4
14.5
14.6
14.7
14.8
Der Dichtematrix - Formalismus . . . . .
Separation von Korrelationsfunktionen .
Entwicklung in einer Einteilchenbasis . .
Erhaltungssatze . . . . . . . . . . . . . .
Die Vlasov Gleichung . . . . . . . . . . .
Der Stoterm nach Uehling-Uhlenbeck .
Die Vlasov-Uehling-Uhlenbeck Gleichung
Storaten, mittlere freie Weglange . . . .
4
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
127
128
128
131
131
132
135
135
137
139
140
142
144
148
149
Einfu
 hrung
Im Rahmen der klassischen Mechanik ist es prinzipiell moglich, die zeitliche Entwicklung
eines Systems von N Teilchen durch Losen der Bewegungsgleichungen (3N) vollstandig
und eindeutig zu berechnen, wenn die Anfangsbedingungen (6N) bekannt sind. Unter
Teilchen verstehen wir { je nach der physikalischen Problemstellung { sowohl Elementarteilchen wie Elektronen, Protonen etc. als auch zusammengesetzte Teilchen wie Atome,
Molekule, Ionen. Fur makroskopische Dimensionen (Teilchenzahl 1023) wird das obige
Verfahren der Losung von Bewegungsgleichungen fragwurdig:
1. Die Losung von 3N gekoppelten Dierentialgleichungen wird fur groe Werte N praktisch undurchfuhrbar.
2. Die notwendige Kenntnis der 6N Anfangsbedingungen wurde eine Unzahl von Messungen erfordern.
3. Die Losung der Bewegungsgleichungen liefert uberussige Information: interessant (weil
leicht mebar und/oder gezielt veranderbar) sind makroskopische Eigenschaften wie Volumen, Druck, Temperatur, elektrischer Widerstand, Polarisation, Magnetisierung etc.,
nicht jedoch Position und Geschwindigkeit eines jeden einzelnen Teilchens.
Dem Ziel der Berechnung makroskopischer Eigenschaften von Systemen mit sehr vielen
Teilchen auf der Basis des mikroskopischen Aufbaus der Materie dient die statistische
Mechanik. Angelpunkt ist das Konzept der statistischen Gesamtheit: anstelle des
tatsachlich vorliegenden Systems betrachtet man eine groe Anzahl von Kopien dieses
Systems, die sich in allen moglichen Zustanden benden konnen, welche die vorgegebenen
makroskopischen Bedingungen (z:B . konstante Gesamtenergie fur ein abgeschlossenes System) erfullen. Eine statistische Geamtheit ist dann charakterisiert durch die Angabe der
Wahrscheinlichkeiten, mit der die mit den makroskopischen Bedingungen vertraglichen
Zustande (oft auch Mikrozustande genannt) in der Gesamtheit vertreten sind. Makrokopische Eigenschaften, die eine zeitliche und raumliche Mittelung uber das betrachtete
System implizieren, werden dann als Mittelwerte uber die statistische Gesamtheit verstanden. Das Konzept der statistischen Gesamtheit setzt zusammen mit den klassischen
Bewegungsgleichungen den Rahmen der klassischen statistischen Mechanik.
Die Grenzen der klassischen statistischen Mechanik liegen dort, wo die Teilchen des zu untersuchenden Systems nach den Gesetzen der Quantentheorie beschrieben werden mussen,
denen grundsatzlich (unabhangig davon, ob das System aus sehr vielen oder nur einigen
wenigen besteht) Wahrscheinlichkeitscharakter anhaftet. Selbst bei maximaler Information uber das System, d:h bei Kenntnis der Wellenfunktion , erhalten wir nur Wahrscheinlichkeitsaussagen uber eine Gesamtheit von Systemen, welche gleichartig und in
gleicher Weise vollstandig prapariert sind. Wir sprechen in diesem Fall von einer reinen
Gesamtheit. Haug { insbesondere im Fall vieler Teilchen { kennen wir den Zustand des
Systems nicht vollstandig, wir wissen nur, das es sich mit gewissen Wahrscheinlichkeiten pm in den Zustanden jm > bendet. (Beipiel: Wahrscheinlichkeiten fur die beiden
Spineinstellungen in einem teilweise polarisierten Strahl freier Elektronen).
Eine solche
P
gemischte Gesamtheit wird durch den statistischen Operator = m pmjm >< mj
beschrieben. Den Erwartungswert einer Observablen A erhalt man, indem man zunachst
< m jAjm > bildet (quanten- mechanischer Mittelwert) und die erhaltenen Werte
5
mit den Gewichten pm aufsummiert (statistischer Mittelwert).
Dem statistischen Operator korrespondiert eine klassische Groe, die Dichtefunktion
kl im Phasenraum der klassischen Variablen qi, pi . Man kann daher auch direkt Quantenstatistik und klassische Statistik miteinander verknupfen. In dieser Vorlesung werden
wir, von der Quantenmechanik ausgehend, die Quantenstatistik aufbauen und daraus die
klassischen Begrie und Ergebnisse ableiten.
Schema
Die statistische Mechanik lat sich grob in zwei Gebiete aufteilen: die Behandlung des
statistischen Gleichgewichts (@=@t = 0) und die Beschreibung von Nichtgleichgewichtsphanomenen (@=@t 6= 0), insbesondere den U bergang ins statistische Gleichgewicht. Der Schwerpunkt dieser Vorlesung wird auf der Behandlung des statistischen
Gleichgewichts und der Berechnung konkreter, makroskopischer Eigenschaften wie spezischer Warme oder Suszeptibilitat liegen. Erst gegen Ende der Vorlesung werden Konzeptionen der Statistischen Mechanik fur dynamische Syteme weit ab vom Gleichgewicht
vorgestellt.
Die statistische Mechanik bringt gegenuber der phanomenologischen Thermodynamik einen wesentlichen Fortschritt: Die Thermodynamik liefert nur Relationen zwischen
verschiedenen makroskopischen Groen; die statistische Mechanik erlaubt die Berechnung
makroskopischer Groen direkt aus den zugrunde liegenden mikroskopischen (atomistischen) Eigenschaften des betrachteten Systems.
6
Teil I
Elementare Quantenmechanik der
Vielteilchensysteme
7
Kapitel 1
Identische Teilchen
Wir wollen uns im folgenden mit der Behandlung von Systemen identischer Teilchen
befassen, also von Systemen, die z:B . nur Elektronen, nur Nukleonen oder nur 4He-Atome
enthalten. Kompliziertere Systeme, wie z:B . ein Gasgemisch, konnen daraus aufgebaut
werden.
1.1 Konzept identischer Teilchen
a) Klassische Mechanik
Fur den prinzipiellen Vergleich zwischen der klassischen Mechanik und der Quantenmechanik genugt es, zwei identische Teilchen zu betrachten. Wir nennen zwei Teilchen
identisch, wenn alle Observablen symmetrisch gegen Teilchenvertauschung sind,
Akl:(1; 2) = Akl:(2; 1):
(1.1)
Im Rahmen der klassischen Mechanik bewegen die beiden identischen Teilchen sich auf
einzelnen Bahnen, die eindeutig festgelegt sind, sofern man die gema (1.1) symmetrische
Hamiltonfunktion
Hkl:(1; 2) = Hkl:(2; 1);
(1.2)
kennt, und Ort und Impuls beider Teilchen zu irgendeiner Zeit t = t0 vorgegeben sind. Aus
den Bewegungsgleichungen folgen dann in eindeutiger Weise die Bahnkurven r1(t) und
r2(t). Da es sich um identische Teilchen handelt, bleibt zunachst oen, welchem Teilchen
man welche Bahn zuordnet. Diese Willkur stellt aber keine Schwierigkeit dar: hat man zu
irgendeiner Zeit t die Zuordnung vorgenommen, so bleibt diese im Laufe der Zeit erhalten;
jedes Teilchen bewegt sich auf seiner Bahn weiter. In diesem Sinne sind identische Teilchen
in der klassischen Mechanik unterscheidbar.
b) Quantenmechanik
Da in der Quantenmechanik der Bahnbegri auf Grund des Zerieens von Wellenpaketen verloren geht, sind identische Teilchen in der Quantentheorie ununterscheidbar.
Um die Konsequenzen dieser Feststellung zu untersuchen, beachten wir, da { analog
8
der klassischen Mechanik { jede beliebige Observable eines Systems identischer Teilchen
symmetrisch bzgl. Teilchenvertauschung sein mu,
A(1 ; 2) = A(2 ; 1);
(1.3)
denn andernfalls gabe es eine Unterscheidungsmoglichkeit. 1; 2 steht fur die Koordinaten
der betrachteten Teilchen, -Ort, Spin, Isospin. Da speziell auch fur den Hamiltonoperator
gilt:
H (1; 2) = H (2; 1);
(1.4)
ist mit jeder Losung (1; 2; t) der Schrodinger-Gleichung
@ ( ; ; t) = H ( ; )( ; ; t)
ih @t
(1.5)
1 2
1 2
1 2
auch (2; 1; t) Losung von (1.5). Fur ein System identischer Teilchen gibt es also auer
den vom Einteilchenproblem bekannten Moglichkeiten der Entartung: die Austauschentartung.
Beispiel: Von zwei unabhangigen, identischen Teilchen, die sich in einem OszillatorPotential bewegen, kann z:B . ein Teilchen sich im 1s { Zustand, das andere im 1p {
Zustand benden. Die Wellenfunktion
und
(1; 2) = '1s(1)'1p(2)
(1.6)
(2; 1) = '1s(2)'1p(1)
(1.7)
[H; 12 ] = 0;
(1.10)
sind dann entartet.
Diese experimentell nicht behebbare Austauschentartung zerstort die Moglichkeit einer eindeutigen Beschreibung eines vollstandig praparierten Systems durch einen Hilbert
- Vektor. Um diese fundamentale Annahme der Quantentheorie beibehalten zu konnen,
mu man im Falle identischer Teilchen ein weiteres Postulat { das Pauli-Prinzip { hinzunehmen: Fur ein System identischer Teilchen sind nur solche Zustande realisierbar, die
entweder total symmetrisch oder total antisymmetrisch bzgl. Teilchenvertauschung sind.
Fur unseren Fall von zwei identischen Teilchen bedeutet dies, da als mogliche Zustande
nur die Kombinationen
s(1; 2) = (1; 2) + (2; 1)
(1.8)
fur Bosonen und
a(1; 2) = (1; 2) , (2; 1)
(1.9)
fur Fermionen in Frage kommen. Eine solche Einteilung der moglichen Zustande eines
Systems identischer Teilchen in zwei Klassen { Bosonen und Fermionen { gibt es in der
klassischen Mechanik nicht.
Die im Pauli-Prinzip ausgesprochene Einengung des Zustandsraumes auf total symmetrische oder total antisymmetrische Zustande ist mit der Dynamik kompatibel, d:h. ein
symmetrischer Zustand bleibt fur alle Zeiten symmetrisch, ein antisymmetrischer Zustand
bleibt antisymmetrisch. Aus (1.4) folgt namlich, da
9
wenn 12 den Operator der Teilchenvertauschung bezeichnet. Die Eigenzustande von H
lassen sich also stets so wahlen, da sie auch Eigenzustande von 12 sind: die Gleichungen
H (1; 2)(1; 2) = E (1; 2)
(1.11)
12(1; 2) = p (1; 2)
(1.12)
sind simultan losbar. Da zweimalige Permutation zum Ausgangszustand zuruckfuhrt,
212 (1; 2) = 12(2; 1) = (1; 2)
(1.13)
folgt
p2 = 1 ! p = 1:
(1.14)
Die Eigenwerte von p = 1 von 12 , die genau zu den nach dem Pauli-Prinzip einzig
moglichen Zustanden fuhren, sind wegen (1.10) gute Quantenzahlen. Das Pauli-Prinzip
ist also mit der Dynamik des Systems kompatibel. Auch durch einen Eingri von auen in Form einer Storung H 0 ist kein U bergang moglich zwischen symmetrischen und
antisymmetrischen Zustanden, denn
< sjH 0ja >=< sj12H 0ja >=< sjH 012 ja >= , < sjH 0ja >= 0; (1.15)
da analog (1.4) auch H 0(1; 2) = H 0(2; 1) sein mu. Damit ist die lineare Konsistenz
von Pauli-Prinzip und Quantentheorie nachgewiesen.
1.2 Statistik
Da der Unterschied des Konzepts identischer Teilchen in der klassischen Mechanik und
in der Quantenmechanik nicht rein akademisch ist, sondern handfeste Konsequenzen hat,
zeigt das folgende einfache Beispiel: Wir betrachten ein System aus zwei identischen
Teilchen, die sich nur in zwei moglichen Einteilchenzustanden , aufhalten konnen.
Dann gibt es folgende Verteilungsmoglichkeiten:
1. Klassische Teilchen
Hier konnen
(1) beide Teilchen im Zustand (2) beide Teilchen im Zustand (3) ein Teilchen in , das andere in sein. Fall (3) kann wegen der Unterscheidbarkeit auf zweierlei Weise realisiert werden.
Daher kommen den drei Moglichkeiten im statistischen Mittel folgende Gewichte zu:
(1) (2) (3)
1
4
1
4
1
2
2. Fermionen
10
(1.16)
Hier sind die Moglichkeiten (1) und (2) verboten, also lauten die Gewichtsfaktoren:
(1) (2) (3)
0 0 1
(1.17)
und Fall (3) ist realisiert durch die Wellenfunktion '(1)' (2) , '(2)' (1).
3. Bosonen
Die Anordnungen (1) und (2) sind moglich, jedoch kann im Unterschied zu 1. Fall (3) nur
auf eine Weise verwirklicht werden, da der Gesamtzustand symmetrisch sein mu. Die
Gewichtsfaktoren und Wellenfunktionen sind also:
1
(1)
3 ' (1 )' (2 )
1
(2)
(1.18)
3 ' (1 )' (2 )
1
'
(
)
'
(
)
+
'
(
)
'
(
)
(3)
1 2
1 2
3
1.3 Pauli-Prinzip fur N identische Teilchen
Analog dem Fall fur zwei Teilchen verlangen wir fur N identische Teilchen, da nur solche
Zustande moglich sind, fur die bei beliebig herausgegrienem Teilchenpaar (i; j ) entweder
oder
ij (1; ::::; N ) = +(1; ::::; N )
(1.19)
ij (1; ::::; N ) = ,(1; ::::; N )
(1.20)
12 = +
(1.21)
ij = 1j 2i12 1j 2i ;
(1.22)
gilt.
Diese Forderung ist in sich widerspruchsfrei: wenn fur irgendein Teilchenpaar (i; j )das +
(,) gilt, so auch fur jedes andere Teilchenpaar des betrachteten Systems. Wenn namlich
fur (1.2) gilt
so folgt mit
da
ij = 12 = +
(1.23)
unabhangig davon, ob 1j und 2i im Zustand den Eigenwert +1 oder -1 haben, da
diese Operatoren in (1.22) jeweils zweimal auftreten.
11
1.4 Zusammengesetzte Teilchen
Alle bislang bekannten Elementarteilchen lassen sich als Bosonen oder Fermionen klassizieren. Dabei gilt ohne Ausnahme, da Bosonen ganzzahligen Spin, Fermionen halbzahligen Spin haben. Beispiele: Fermionen sind z:B . Elektronen, Protonen, Neutronen, Neutrinos -Spin 1=2 -Teilchen -; dagegen sind Photonen, Pionen, Phononen (
Gitterschwingungen in Kristallen) Bosonen. Atomkerne sind Bosonen bei gerader, Fermionen bei ungerader Nukleonenzahl, vorausgesetzt, da man die 'Atomkerne' als Teilchen
behandeln darf. Dies ist der Fall in Molekul- und Festkorperphysik. Zum Beweis der oben
behaupteten Eigenschaft von Atomkernen betrachten wir zwei gleiche Kerne mit je Z
Protonen und N Neutronen, { insgesamt also 2Z + 2N = 2A Teilchen. Vertauschung
der beiden Kerne bedeutet dann Vertauschung der Nukleonen des einen Kerns mit denen
des anderen, { dies sind insgesamt A Vertauschungen. Da die Wellenfunktion bei jeder
einzelnen Vertauschung zweier Fermionen das Vorzeichen wechselt, gilt
12 = (,)A ;
(1.24)
wenn 12 der Operator der Vertauschung der beiden identischen Kerne ist. Die Erweiterung auf mehr als zwei identische Kerne ist trivial; es gilt also wie behauptet: Kerne
mit gerader Nukleonenzahl verhalten sich wie Bosonen (z:B . 3 He). Diese Eigenschaften
zusammengesetzter Teilchen werden sich z:B . bei der Berechnung der spezischen Warme
eines idealen Gases zweiatomiger Molekule als wesentlich erweisen.
12
Kapitel 2
Teilchenzahldarstellung fur
Fermionen
2.1 Darstellung im Kongurationsraum
Den Zustand eines Systems N identischer Teilchen mit Koordinaten (Ort, Spin, evtl.
Isospin) i ; i = 1; :::; N , kann man durch eine Wellenfunktion im Kongurationsraum
(1; ::::; N ; t)
(2.1)
beschreiben (vgl. Quantentheorie). Fur die Berechnung von aus der Schrodinger-Gleichung
des N - Teilchensystems
@ ( ; :::; ; t) = H ( ; ::::; ; t)
ih @t
(2.2)
1
N
1
N
ist man im allgemeinen auf Naherungsverfahren angewiesen. Die am haugsten benutzten
Naherungsverfahren beruhen letzten Endes alle darauf, da man den Hamiltonoperator
H aufteilt,
wobei
H := H0 + HR ;
H0(1; ::::; N ) =
N
X
i=1
h(i) =
N
X
(2.3)
i=1
[ti + U ( )]
(2.4)
ein System unabhangiger Teilchen in einem mittleren Potential U beschreibt und HR die
verbleibende Restwechselwirkung zwischen den Teilchen erfat.
Beispiel: Fur die Elektronen eines Atoms konnte man als U ( ) ein abgeschirmtes CoulombPotential benutzen, welches die Kern-Elektronen-Wechselwirkung exakt und die ElektronElektron-Wechselwirkung naherungsweise im Sinne eines mittleren Potentials erfat. Der
Ansatz (2.3) bildet dann zusammen mit dem Pauli-Prinzip die Grundlage des Schalenmodells der Atomphysik.
13
Die Schrodinger-Gleichung fur H0 lat sich streng losen (fur vernunftige Potentiale U ),
da die Aufgabe sich auf ein Einteilchenproblem
h '( ) = '( )
reduziert. Die Eigenfunktionen zu H0 sind dann einfach Produktfunktionen
(2.5)
fg = 'i1 (1) 'iN (N );
(2.6)
wobei fg die jeweils herausgegrienen Einteilchenzustande i1 :::::iN charakterisiert. Wenn
die Eigenfunktionen zu h ein vollstandiges System bilden (welches wir im folgenden
stets als orthonormiert annehmen wollen), so bilden die Produktfunktionen fg eine
vollstandige Basis im Kongurationsraum.
Die allgemeine N -Teilchen-Wellenfunktion (1; ::::; N ; t) kann dann als Linearkombination der Produktfunktionen fg aufgebaut werden.
=
X
fg
Cfg (t)fg:
(2.7)
Die Koezienten Cfg (t) sind dabei aus der Schrodinger-Gleichung (2.2) zu bestimmen.
Will man z:B . die stationaren Losungen von (2.2) berechnen, so besteht ein Verfahren
darin, die Koezienten Cfg durch Diagonalisieren von HR in der Basis fg zu bestimmen: man greift aus der Basis der fg endlich viele (die energetisch gunstigsten) heraus
und diagonalisiert die endlichdimensionale Matrix
< fgjHRjf0g >;
(2.8)
womit gema Konstruktion der fg die Diagonalisierung von H gesichert ist; durch
Hinzunahme weiterer Produktfunktionen lat sich dieses Naherungsverfahren systematisch verbessern.
Da wir Systeme identischer Teilchen betrachten, mu die resultierende N -TeilchenWellenfunktion - in jedem Schritt eines Naherungsverfahrens - dem Pauli-Prinzip genugen.
Dies ist z:B . in der oben skizzierten Methode nicht automatisch der Fall, da die Matrix
(2.8) nicht wei, ob wir Bosonen oder Fermionen betrachten. Es ist daher zweckmaig,
die erforderliche Antisymmetrisierung direkt an den Basisfunktionen vorzunehmen, nach
denen entwickelt wird. Analog dem Fall von zwei identischen Teilchen bilden wir antisymmetrisierte Produktfunktionen in Form von Slater-Determinanten
a fg = p1
(,)pP ['i1 (1) 'iN (N )];
(2.9)
N! p
wobei P alle moglichen Permutationen durchlauft. Nach den Regeln uber Determinanten ist a fg total antisymmetrisch bzgl. Teilchenvertauschung ( Vertauschung zweier
Spalten bzw. Reihen). Insbesondere ist a fg = 0 sobald irgend zwei Funktionen 'i aus
dem betrachteten Satz fg ubereinstimmen. Damit lat sich das Pauli-Prinzip fur ein System unabhangiger Fermionen auch so formulieren, da jeder Einteilchenzustand nur
einfach besetzt werden darf. Diese Formulierung des Pauli-Prinzips setzt allerdings
unabhangige Fermionen voraus (HR 0) und ist somit nur ein Spezialfall von (1.20)!
X
14
Die Entwicklung von in der Basis (2.9) garantiert, da die Losungen in jedem Schritt
eines darauf aufbauenden Naherungsverfahrens dem Pauli-Prinzip genugen; sie ist von
praktischem Vorteil, da die Entwicklung von in der Basis a fg weniger zu berechnende Entwicklungskoezienten enthalt als die Entwicklung (2.7). Als allgemeinen Ansatz
wahlen wir also
(1; ::::; N ; t) =
X
fg
Cfag (t)a fg:
(2.10)
Durch optimale Wahl von U ( ) kann man versuchen, HR so klein zu halten, da das
System in guter Naherung durch H0 beschrieben wird, da sich die Teilchen also naherungsweise unabhangig verhalten. Dies ist z:B . in der Atomphysik fur viele Fragestellungen (Beispiel: Aufbau des periodischen Systems der Elemente) eine gute Naherung. Der
Grundzustand des Systems wird dann approximiert durch den Grundzustand von H0, in
dem die niedrigsten N Einteilchenzustande 'i besetzt sind. Dieser Zustand ist nicht immer
eindeutig deniert: Wenn entartete Einteilchenzustande vorliegen (was z:B . in Zentralpotentialen stets der Fall ist), kann je nach der Teilchenzahl des Systems der niedrigste
Eigenzustand von H0 entartet sein, z:B . wenn beim Besetzen der Einteilchenzustande
fur das letzte Teilchen zwei oder mehr energetisch gleiche Niveaus zur Verfugung stehen.
Angeregte Zustande des N -Teilchen-Systems erhalt man { in der Naherung unabhangiger
Teilchen! { indem man ein oder mehrere Teilchen im Niveau anhebt, die im Grundzustand
unbesetzt sind (Teilchen-Loch-Anregungen), siehe Skizze.
2.2 Aufbau des Fock-Raumes
Die im folgenden zu besprechende Teilchenzahldarstellung besitzt gegenuber der Kongurationsraum-Darstellung zwei wesentliche Vorteile:
1. Wahrend die Wellenfunktionen (1; :::; N ; t) Systeme mit fester Teilchenzahl N beschreiben, erlaubt die Teilchenzahldarstellung die Beschreibung von Systemen, deren Teilchenzahl unscharf ist. Eine solche Darstellung ist im Rahmen der statistischen Mechanik von Bedeutung, da einerseits in der Praxis die Teilchenzahl eines makroskopischen
Systems nicht genau bekannt ist, andererseits auch solche Systeme interessieren, die mit
ihrer Umgebung Teilchen austauschen konnen (vgl. die Diskussion der grokanonischen
Gesamtheit in Teil II).
2. Die Antisymmetrisierung lat sich in der Teilchenzahldarstellung in Form weniger, einfacher Vertauschungsrelationen fur Teilchen-Erzeugungs | bzw. Vernichtungs- Operatoren erfassen. Dadurch entsteht ein Kalkul, welcher einfacher und sicherer zu handhaben ist als der Umgang mit Slater-Determinanten im Rahmen der KongurationsraumDarstellung.
Wir betrachten im folgenden ein System von Fermionen, dessen Teilchenzahl nicht
scharf ist. Ein solches System beschreiben wir im sogenannten Fock-Raum, der aus der
Gesamtheit der Hilbert-Raume HN zu fester Teilchenzahl wie folgt aufgebaut wird:
H1 sei der Hilbert-Raum eines 1-Fermionen-Systems, aufgespannt durch Vektoren ji >;
deren Darstellung im Kongurationsraum die Wellenfunktionen 'i( ) sind,
15
ji > 'i( ):
(2.11)
i steht hier fur einen vollstandigen Satz von Quantenzahlen fur ein Teilchen.
H2 sei der Hilbert-Raum eines 2-Fermionen-Systems, aufgespannt durch Vektoren ji1i2 > :
Ein solcher Vektor ji1i2 > beschreibt einen Zustand, in dem die Einteilchen- Zustande
i1, i2 besetzt sind; die Kongurationsraum-Darstellung dieser Zustande ji1i2 > sind 2x2
Slater-Determinanten, gebildet mit den Wellenfunktionen 'i1 , 'i2 ,
ji1i2 >= p12 ''ii1 ((11)) ''ii1 ((22)) :
2
2
(2.12)
Allgemein:
HN sei der Hilbert-Raum eines N -Fermionen-Systems, aufgespannt durch Vektoren ji1::::iN >.
Die Schreibweise ji1:::::iN > meint, da die Einteilchenzustande i1 , i2; :::, iN gema dem
Pauli-Prinzip je einfach besetzt sind. Im Kongurationsraum werden die Vektoren ji1:::::iN >
16
dargestellt durch N -Teilchen Slater-Determinanten, gebildet aus den Einteilchenfunktionen 'i1 ; ::::, 'iN :
X
ji1 ::::iN >= p1 (,)p P ['i1 (1):::::'iN (N )]:
(2.13)
N! p
Phasenfestlegung:
Um in der Determinante (2.13) das Vorzeichen eindeutig festzulegen, mussen die Funktionen 'i in beliebiger, aber fester Weise numeriert werden (Vertauschung zweier Indizes
bedeutet Zeilenvertauschung, also Vorzeichenwechsel!). Wir konnen z:B . die Funktionen
'i nach wachsender Einteilchenenergie i ordnen. Sind mehrere 'i entartet, so ordnen wir
bei fester Energie z:B . nach zunehmendem Drehimpuls j und Komponente mj , jeweils
bei ,mj beginnend. auf diese Weise schaen wir uns eine Standard-Ordnung
i1 < i2 < :::: < iN ;
(2.14)
die beliebig ist, aber innerhalb einer Rechnung konsequent beibehalten werden mu. Damit
ist auch die Index-Ordnung in ji1::::::iN > fest!
In jedem Hilbert-Raum HN sind die Vektoren ji1 ::::iN > auf Grund der Korrespondenz
mit Slater-Determinanten orthonormiert,
< i1 :::iN jj1::::jN >= i1 j1 :::::::in jn ;
wenn die Einteilchenfunktionen 'i orthonormiert sind.
Beweis: Wir schreiben
wobei der Operator
p
(2.15)
a fig = N ! A['i1 (1) 'iN (N )]
(2.16)
A := N1 ! (,)pP
(2.17)
X
p
auf den Raum der antisymmetrisierten N -Teilchen-Funktionen projiziert. Als Projektionsoperator hat er die charakteristischen Eigenschaften
A = Ay; A2 = A;
(2.18)
wie man auch explizit an Hand von (2.17) beweisen kann (vgl. etwa A. Messiah, Quantum
Mechanics II, p. 97). Wir bilden nun:
< a figjafj g >= N ! < A figjA fj g >
(2.19)
wobei fig = 'i1 (1) 'iN (N ), fj g = 'j1 (1) 'jN (N ) die reinen Produktfunktionen sind. Mit (2.18) wird
< a figjafj g >= N ! < figjA2fj g >= N ! < figjA fj g > :
Entwickelt man A fj g gema (2.17), so wird:
17
(2.20)
N ! < figjA fj g >= det(< 'in j'jm >):
(2.21)
Dieser Ausdruck ist nur 6= 0, wenn die Folgen fi1 ::::iN g und fj1 ::::jN g ubereinstimmen,
da andernfalls in jedem Produktterm der Entwicklung von det(< 'in j'jm >) mindestens
1 Faktor = 0 ist. Die Normierung der 'i garantiert dann, da auch
< i1 :::iN ji1 :::iN >= 1
(2.22)
wird.
Unter Hinzunahme des Raumes H0 fur das Teilchen-Vakuum mit dem einzigen Zustand
j0 > fassen wir nun die Raume H0 , H1; :::, HN als direkte Summe zusammen zum FockRaum H;
H = H0 H1 H2 ::::: HN ::::
(2.23)
Das in den einzelnen Raumen Hi schon denierte Skalarprodukt erganzen wir durch
< i1 :::iN jj1 :::jM >= 0
(2.24)
fur N 6= M:
Damit ist im gesamten Fock-Raum ein Skalar-Produkt eingefuhrt; die in (2.24) getroffene Wahl steht uns frei, weil ein Skalar-Produkt zwischen Slater-Determinanten a fg
mit unterschiedlicher Teilchenzahl nicht erklart ist. Wir sind also { im Gegensatz zu (2.15)
{ in Gl. (2.24) nicht durch die Korrespondenz zum Kongurationsraum gebunden.
Die in (2.24) getroene Wahl bedeutet, da wir die Unterraume Hi in orthogonaler
Weise zusammengesetzt haben. Diese Wahl ist auch die einzig sinnvolle im Hinblick auf
Operatoren, welche die Teilchenzahl erhalten, z:B . den Teilchenzahl-Operator N^ selbst.
Dieser Operator ist per Denition in jedem Unterraum Hi diagonal,
N^ ji1 :::iN >= N ji1 :::iN > :
(2.25)
Damit nun die Eigenschaft (2.25) auch in H gultig bleibt, mu gerade (2.24) gefordert
werden, womit
< i1 :::iN jN jj1::::jM >= N < i1 :::iN jj1 :::jM >= M < i1:::iN jj1 :::jM >
(2.26)
fur N 6= M . Damit sind alle Basisvektoren in H orthonormiert, wenn man noch hinzunimmt
< 0j0 >= 1;
(2.27)
da die Korrespondenz zwischen den Vektoren ji1:::iN > und den Slater-Determinanten
uber das Skalarprodukt < 0j0 > keine Aussage liefert. (Achtung: man verwechsle den
Vakuumzustand j0 > nicht mit dem Nullvektor).
18
2.3 Erzeugungs- und Vernichtungs-Operatoren
Wir fuhren nun in H lineare Operatoren ein. Die beiden Grundtypen, aus denen sich alle
anderen aufbauen lassen, sind Erzeugungs- bzw. Vernichtungs-Operatoren fur Teilchen.
Erzeugungs-Operatoren sollen die Unterraume HN fur verschiedene Werte N in folgender
Weise verknupfen:
aym ji1:::iN >= 0 falls m besetzt
(2.28)
aym ji1:::iN >= jmi1 :::iN >= (,)k ji1 ::i; im ; :::iN > sonst:
Die naturliche Zahl k bezeichnet die Zahl der in ji1 ::::iN > besetzten Zustande, welche
dem Zustand m in der verabredeten Standard-Ordnung vorangehen. Der Faktor (,)k
in (2.28) ruhrt also daher, da bei Vertauschung von je zwei Teilchen, d:h. von je zwei
besetzten Zustanden, der Vektor ji1:::iN > wegen der Antisymmetrie sein Vorzeichen
andert.
Die Interpretation von (2.28) liegt auf der Hand: Der Operator aym erzeugt ein Teilchen
im Zustand m, falls dieser in ji1 :::iN > nicht besetzt ist; die Operatoren aym fur verschiedene
m-Werte fuhren also von HN nach HN +1. Ist m in ji1:::iN > besetzt, so konnen wir wegen
des Pauli-Prinzips nicht noch ein zweites Teilchen in m erzeugen. Es gilt daher allgemein:
wegen des Pauli-Prinzips.
(aym )2 = 0 8m
(2.29)
Folgerungen aus der Denition (2.28):
1. Vernichtungs-Operatoren
Die zu den Operatoren aym adjungierten Operatoren am sind Teilchenvernichtungs-Operatoren. Zum Beweis zerlegen wir den Einheitsoperator in H gema der VollstandigkeitsRelation
X
X
jj1::::jM >< j1 :::jM j = 1H0 1H1 1H2 ::::::: = 1H:
(2.30)
M 0 fjM g
Dann konnen wir schreiben
am ji1:::iN >= 1Ham ji1 ::::iN >=
X
X
M 0 fjM g
jj1 :::jM >< j1 :::jM jamji1 :::iN >;
(2.31)
und fur die Koezienten < j1 :::jM jamji1:::iN > gilt
< j1 :::jM jamji1:::iN >=< i1 :::iN jaymjj1 :::jM >
(2.32)
nach Denition des adjungierten Operators. Weiter ist:
< i1 :::iN jaymjj1 :::jM > =< i1 :::iN jmj1 :::jM >= (,)k < i1:::iN jj1 ::jk m::jM > : (2.33)
Nun ist < i1:::iN jj1 ::jk m::jM >6= 0 nur dann, wenn a) N = M + 1 wegen der Orthogonalitat der Raume HN und b) die Folgen (i1:::iN ) und (j1 ::jk m::jM ) ubereinstimmen. Also
wird:
am ji1::::iN >= 0 falls m in ji1:::iN > leer
(2.34)
19
am ji1::::iN >= (,)k ji1 :::ik ; :; ik+2::iN > falls m besetzt und m = ik+1:
In (2.31) tragt von der Doppelsumme also nur ein Vektor aus HN ,1 bei und zwar gerade
derjenige, der (bis auf das Vorzeichen) aus dem Vektor ji1:::iN > hervorgeht, wenn man
den Zustand m = ik+1 auslat. Also: am vernichtet ein Teilchen im Zustand m, falls m in
ji1:::iN > besetzt ist.
2. Aufbau von N -Teilchen-Zustanden aus dem Vakuum
Einen N -Teilchen-Zustand ji1 :::iN > erhalten wir durch Anwendung von ErzeugungsOperatoren auf das Vakuum,
jiN :::i1
>= ay
iN
iN
Y
y
::::a j0 >=
ay
i1
m=i1
m j0 > :
(2.35)
Naturlich ist
ayi1 :::ayiN j0 >= (,)N (N ,1)=2 ayiN :::ayi1 j0 >;
(2.36)
wenn man die oben durchgefuhrten U berlegungen zur Phasenfestlegung beachtet. Das
Vakuum ist dadurch gekennzeichnet, da
am j0 >= 0 8m:
(2.37)
aym am ji1::::iN >= 0 falls m in ji1 ::iN > leer
(2.38)
3. Teilchenzahl-Operator N^
Aus (2.28) und (2.34) folgt
aym am ji1::::iN >= ji1 :::iN > falls m in ji1 ::iN > besetzt:
Der Operator aym am hat also die Zustande ji1 :::iN > als Eigenzustande mit den Eigenwerten 0 und 1,
aymam ji1 :::iN >= nm ji1 :::iN >; nm = 0; 1;
(2.39)
d:h. aym am gibt an (mit), ob der Zustand m besetzt ist (nm = 1) oder leer (nm = 0):
Der Operator m aym am fragt daher alle Einteilchenzustande ab, ob sie besetzt sind
oder nicht und addiert die Zahl der besetzten Zustande auf; er bestimmt also die Teilchenzahl des betrachteten Systems. Es ist somit
N^ = aym am
(2.40)
P
X
m
eine explizite Darstellung des Teilchenzahl-Operators, dessen Eigenwerte zu den Eigenvektoren ji1:::iN > die Teilchenzahl N des Systems ergeben. N^ ist gema (2.40) oensichtlich
hermitesch. In einem beliebigen Zustand aus H
j(t) >=
X X
N 0 fjN g
CfNjN g(t)jj1 ::::jN >
ist N^ allerdings unscharf.
20
(2.41)
4. Vertauschungsregeln
Aus der Denition der aym folgt
aym aynji1 :::iN >= 0 falls m; n besetzt oder n = m
aym aynji1 :::iN >= jmni1:::iN >
und umgekehrt,
(2.42)
sonst
aynaym ji1:::iN >= 0 falls n; m besetzt oder n = m
aynaym ji1:::iN >= jnmi1 ::iN >= ,jmni1 ::iN >
Addition von (2.42) und (2.43) ergibt
(2.43)
sonst:
aym ayn + aynaym = 0;
(2.44)
da (2.42) und (2.43) fur jeden beliebigen Vektor ji1:::iN > gilt. Analog beweist man (U B):
am an + anam = 0:
(2.45)
Schlielich gilt noch:
aym an + anaym = mn :
(2.46)
Anmerkung: Die Vertauschungs-Relationen (2.44), (2.45) und (2.46) werden komplizierter, wenn man eine nicht-orthogonale Basis von Einteilchen-Funktionen benutzt.
2.4 Observable in der Teilchenzahl-Darstellung fur
feste Teilchenzahl
Um im Fock-Raum Physik treiben zu konnen, mussen wir Operatoren wie kinetische
Energie T , potentielle Energie V oder Drehimpuls J explizit darstellen konnen. Wir wollen
zeigen, da Operatoren wie die oben erwahnten sich aus den ai, ayi aufbauen lassen.
Dabei nutzen wir aus, da uns die Darstellung der oben genannten Operatoren im
Kongurationsraum bekannt ist (vgl. Quantentheorie). Die korrespondierenden Operatoren im Fock-Raum H sind dann so zu denieren, da die Matrixelemente eines Operators
in den Unterraumen HN in beiden Darstellungen gleich sind. Es genugt, dies fur die
Basisvektoren zu zeigen:
Z
d a fiN gO(1; ::; N )a fjN g =< i1 :::iN jO^ (aym ; am )jj1:::jN > :
(2.47)
Da die uns interessierenden Operatoren wie Energie oder Drehimpuls die Teilchenzahl
erhalten, mu auer (2.47) noch gelten
< i1 :::iN jO^ (aym ; am )jj1:::jM >= 0
(2.48)
fur N 6= M . Durch die Gleichungen (2.47) und (2.48) ist der gesuchte Operator O^ (aym ; am)
vollstandig in H deniert.
21
Wir interessieren uns im folgenden fur additive Ein- und Zwei-Teilchen Operatoren
und behaupten, da ein beliebiger Einteilchen-Operator
f=
N
X
=1
f ()
und ein beliebiger Zweiteilchen-Operator
X
g = 21 g(; )
6=
die folgende Darstellung im Fock-Raum besitzen:
X
f^ = (mjf jn) aym an
m;n
mit
bzw.
mit
Z
(2.49)
(2.50)
(2.51)
(mjf jn) = d 'm( )f ( )'n( )
(2.52)
g^ = 21
(2.53)
(pqjgjmn) =
X
n;m;p;q
(pqjgjmn) aypayq anam
Z Z
d d 0 'p( )'q ( 0)g(; 0)'m( )'n( 0):
(2.54)
Wie gewunscht erhalten die Operatoren f^ und g^ die Teilchenzahl, da ay und a stets
paarweise auftreten. Also gilt:
[f;^ N^ ] = [^g; N^ ] = 0;
(2.55)
was auch explizit mit Hilfe der Vertauschungs-Relationen fur ay; a bewiesen werden kann.
Mit (2.55) folgt
^ O^ ]jj1:::jM >= (N , M ) < i1 :::iN jO^ jj1:::jM >= 0
< i1 :::iN j[N;
(2.56)
fur O^ = f;^ g^, so da (2.48) erfullt ist,
< i1::iN jO^ jj1 :::jM >= 0
(2.57)
fur N 6= M . Qualitativ ist die Struktur von f^ und g^ sofort verstandlich: Im Kongurationsraum greift jeder Summand von f = N=1 f () an nur ein Teilchen an und verandert
den Zustand dieses Teilchens gema
P
f ()'m() =
X
n
'n()(njf jm):
(2.58)
Genau analog arbeitet f^ im Fock-Raum: Jeder Summand von f^ andert den Zustand
ji1:::iN > derart, da im Zustand n ein Teilchen vernichtet, dafur in m wieder eines
erzeugt wird. Entsprechend: Ein Zweiteilchen-Operator g greift gleichzeitig an jeweils zwei
Teilchen an und andert deren Zustand. Das Gleiche erreicht g^, indem er zunachst zwei
22
Teilchen in den Zustanden m; n vernichtet, anschlieend zwei Teilchen in den Zustanden
p; q erzeugt.
Den Beweis fur (2.51), (2.52) wollen wir explizit durchfuhren, fur (2.53), (2.54) lauft der
Beweis entsprechend. Wegen (2.58) folgt bei Anwendung von f auf eine Produkt-Funktion:
f 'i(1)'j (2) =
(mjf ji)'m(1)'j (2) +
X
m
m
(mjf jj )'i(1)'m(2) + ::::
X
(2.59)
Da wegen der Teilchen-Identitat f in allen Teilchen symmetrisch aufgebaut ist { Andernfalls konnte die Observable f zur Unterscheidung der Teilchen benutzt werden im
Widerspruch zur Annahme identischer Teilchen { gilt
[f; A] = 0
(2.60)
mit A aus (2.17). Anwendung von A auf Gleichung (2.59) ergibt daher
f a fijk:::g =
(mjf ji)a fmjk:::g
X
m
+ (mjf jj )afimk:::g +
X
X
m
m
(mjf jk)afijm:::g + :::
Dieses Ergebnis vergleichen wir mit
X
f^jijk::: >= (mjf jn)ayman jijk::: >
m;n
=
(mjf ji)jmjk::: > +
(2.61)
(2.62)
(mjf jj )jimk::: > + (mjf jk)jijm:: > +::
X
X
X
m
m
m
(Man beachte hier die in (2.28) und (2.34) eingehenden Phasenfaktoren!) Man veriziert
nun leicht die denierende Gleichung (2.47), indem in (2.61) und (2.62) die benotigten
Matrixelemente gebildet und gliedweise verglichen werden.
2.5 Anwendungsbeispiele
1. Grundzustand und einfache Anregungen eines N -Fermionen-Systems
Den Grundzustand erhalten wir, indem wir die N tiefsten Einteilchen-Niveaus i1 , i2 , ...,
iN besetzen:
j0 >= ayiN ayi1 j0 > :
(2.63)
Einteilchen-Einloch-Anregungen haben dann die Form:
j1T ,1L >= aymai j0 >;
wobei m in j0 > leer, i besetzt ist.
23
(2.64)
2. Erwartungswerte
Fur den Erwartungswert der kinetischen Energie in einem N -Teilchen-Zustand ji1:::iN >
erhalt man unter Benutzung von (2.51) sowie (2.28) und (2.34):
X
< i1:::iN jT^ji1:::iN >= (mjtjn) < i1 :::iN jaym anji1:::iN >=
m;n
iN
X
m=i1
(mjtjm);
(2.65)
da erstens nur Werte n beitragen konnen, die in (i1 :::iN ) vorkommen und zweitens wegen der Orthogonalitat verschiedener Zustande ji1 :::iN > m = n sein mu. Der Erwartungswert der kinetischen Energie ist also (wie zu erwarten) die Summe der Beitrage
der vorhandenen Teilchen, d:h. der besetzten Zustande; die analoge Aussage gilt fur den
Drehimpuls, den Impuls oder andere Einteilchen-Operatoren.
Etwas komplizierter wird der Fall der potentiellen Energie (allgemein: eines ZweiteilchenOperators). In
X
< i1 :::iN jV^ ji1:::iN >= 21
(pqjV jmn) < i1 :::iN jaypayq an amji1 :::iN >
(2.66)
m;n;p;q
tragen nur die Werte n 6= m bei, die in ji1:::iN > besetzt sind. Weiterhin mu wegen der
Orthogonalitat der Basiszustande ji1 :::iN > des Fock-Raumes entweder p = m und q = n
oder q = m und p = n sein. Man erhalt daher:
X
< V^ >= 21
f(mnjV jmn) , (mnjV jnm)g;
(2.67)
m;n besetzt
wobei Terme mit m = n sich als Selbst-Wechselwirkungen automatisch wegheben.
Der direkte Term
1 X (mnjV jmn)
(2.68)
2 m;n besetzt
entspricht dem klassischen Wechselwirkungs-Integral:
1 X (mnjV jmn) = 1 X Z Z d d 0j' ( )j2V (; 0)j' ( 0)j2
(2.69)
m
n
2 m;n besetzt
2 m;n
Dabei ist
= 12
Z Z
d d 0 ( )V (; 0)( 0):
( ) =
X
m besetzt
j'm( )j2
(2.70)
die Wahrscheinlichkeitsdichte, ein Teilchen mit der Koordinate vorzunden; sie setzt
sich additiv aus den Beitragen j'm( )j2 der einzelnen Teilchen zusammen.
Beispiel: Coulomb-Energie einer durch beschriebenen Ladungsverteilung.
Der zweite Term in (2.69) ist ein typisch quantenmechanischer Eekt fur Systeme von
Fermionen (Austauschterm); er ist verantwortlich fur die homoopolare Bindung, z:B .
im H2-Molekul.
24
Bemerkung:
Aus historischen Grunden lauft der hier entwickelte Formalismus haug auch unter der Bezeichnung Zweite Quantisierung. Es sollte jedoch klar geworden sein, da die TeilchenzahlDarstellung { abgesehen von der Erweiterung auf Systeme mit unscharfer Teilchenzahl
{ nur eine andere Darstellung als die Kongurationsraum-Darstellung eines Systems N
identischer Teilchen ist. Von einer Zweiten Quantisierung der nichtrelativistischen Quantentheorie von N -Teilchen-Systemen kann nicht die Rede sein!
25
Kapitel 3
Teilchenzahl-Darstellung fur
Bosonen
Dieser Fall lauft weitgehend analog dem der Fermionen; wir werden uns daher auf eine
knappe Darstellung beschranken und nur die Unterschiede Bosonen - Fermionen herausarbeiten.
3.1 Darstellung im Kongurationsraum
N unabhangige Bosonen beschreiben wir im Kongurationsraum durch vollstandig symmetrisierte Produkt-Funktionen.
sfiN g = (N !n ! 1 n !)1=2 P ['i1 (1) 'iN (N )]:
(3.1)
1
N
p
Dabei ist es { im Gegensatz zu den Fermionen { moglich, da ein Einteilchen-Zustand
nj -fach besetzt ist; naturlich ist
nj = N
(3.2)
X
X
j
fur jeden moglichen Zustand (3.1).
Aus den Basiszustanden konnen durch Superposition (im Prinzip) die exakten N Teilchen-Zustande fur wechselwirkende Bosonen aufgebaut werden.
3.2 Fock-Raum fur Bosonen
Den symmetrisierten Produkt-Funktionen (3.1) ordnen wir in der Teilchenzahl-Darstellung
Vektoren
jni1 ni2 :::: >
(3.3)
zu, wobei die Zahlen ni1 , ni2 etc. angeben, welche Einteilchen-Zustande wievielfach besetzt sind. Naturlich gilt wiederum (3.2). Aus der (wie fur Fermionen zu beweisenden)
Orthonormierung der Funktionen sfiN g folgt in der Teilchenzahl-Darstellung
(3.4)
< ni1 ni2 :::jnj1 nj2 ::: >= ni1 nj1 ni2 nj2 :::
26
Die durch die Zustande (3.1) bzw. (3.3) mit der Nebenbedingung (3.2) aufgespannten
Hilbert-Raume HN zu fester Bosonenzahl N setzen wir nun zum Fock-Raum H fur Bosonen analog Kap. 2.1 zusammen: - Groen, die sich auf Fermionen bzw. Bosonen beziehen,
unterscheiden wir nur dort durch ihre Bezeichnungsweise, wo unbedingt notig. Naturlich
ist der Fock-Raum H fur Bosonen von dem fur Fermionen zu unterscheiden! -
H = H0 H1 H2 :::: HN :::
(3.5)
H0 erfat das Bosonen-Vakuum, beschrieben durch den Vektor j0 >; den wir im folgenden
als normiert annehmen,
< 0 j 0 >= 1:
(3.6)
Naturlich ist das Bosonen-Vakuum nicht mit dem Fermionen-Vakuum identisch, j0 >B 6=
j0 >F . Da in Kap. 2 nur Fermionen, hier nur Bosonen behandelt werden, lassen wir die
Indizierung weg (vgl. die vorherige Anmerkung).
Mit der gleichen Begrundung wie in Kap. 2.2 fuhren wir das Skalar-Produkt zwischen
Zustanden unterschiedlicher Teilchenzahl ein durch
< n1n2 :::nk ::jn01 n02:::n0k :: >= 0
falls
X
i
ni 6=
X
j
0
(3.7)
n0j :
(3.8)
Dabei haben wir zur Vereinfachung der Schreibweise die Einteilchen-Zustande mit 1; 2; :::k:.
durchnumeriert; n01 ; n02::. sind die zugehorigen Besetzungszahlen, die im Falle der Bosonen den N -Teilchenzustand eindeutig charakterisieren. (Fur Fermionen sind die Besetzungszahlen entweder 0 oder 1, so da ein N -Teilchenzustand durch die Reihenfolge der
Einteilchenzustande mit Besetzungszahl 1 eindeutig bestimmt ist.) In H sind also nach
Konstruktion alle Basiszustande jn1n2 :::nk ::: > zueinander orthogonal und normiert.
3.3 Erzeugungs- und Vernichtungs-Operatoren
Wir fuhren nun in H lineare Operatoren ein, welche Zustande aus HN mit solchen aus
HN +1 verknupfen:
p
byk j:::nk ::: >= nk + 1 j::::nk + 1:::: >
(3.9)
bk j:::nk ::: >= pnk j:::nk , 1::: > :
Die Operatoren byk erzeugen also jeweils ein Teilchen im Zustand k; bk p
wirkt entsprechend
p
als Vernichtungs-Operator. Mit den in (3.9) gewahlten Vorfaktoren nk bzw. nk + 1
sind - wie in der Schreibweise schon vorweggenommen - byk und bk adjungierte Operatoren.
Beweis: Wir bilden
q
< ::nk ::jbk j:::n0k :: >= n0k nk ;nk ,1
(3.10)
0
und
p
q
< :::n0k ::jbyk j::nk :: >= nk + 1 nk ;nk +1 = n0k nk ,1;nk
0
27
0
(3.11)
Folgerungen:
1. Bosonen-Vakuum
Das Bosonen-Vakuum ist (analog dem Fermionen-Fall) gekennzeichnet durch
bk j0 >= 0 8 k;
(3.12)
wie direkt aus (3.9) folgt. Ausgehend vom Vakuum lassen sich alle anderen Zustande
durch Anwendung von Erzeugungs-Operatoren aufbauen,
X
(byi )ni j0 >= jn1 n2n3 ::: >
(3.13)
mit
i ni
P
= N:
i
2. Teilchenzahl-Operator
Aus (3.9) folgt direkt
byk bk j:::nk ::: >= nk j:::nk :: >;
(3.14)
der Operator byk bk zahlt also die Teilchen im Zustand k. Der Operator der GesamtTeilchenzahl ist also
N^ = byk bk = N^k :
(3.15)
Da oensichtlich
X
X
k
k
^ N^k ] = 0;
[N;
(3.16)
gibt es Zustande in H, in denen sowohl die Gesamt-Teilchenzahl N als auch die Besetzungszahlen nk der Einteilchen-Zustande k scharf sind.
3. Vertauschungs-Relationen
Aus der Denitions-Gleichung (3.9) folgt
bk byk j:::nk ::: >= (nk + 1)j:::nk ::: >
(3.17)
sowie
byk bk j:::nk :: >= nk j:::nk ::: >
(3.18)
(siehe (3.14)), woraus durch Dierenzbildung
(bk byk , byk bk )j:::nk ::: >= j:::nk ::: >
(3.19)
wird. Da j:::nk ::: > beliebig gewahlt war, ergibt sich die Operator-Relation:
bk byk , byk bk = 1:
(3.20)
Alle anderen Kommutatoren verschwinden, wie man analog beweist (U B). Insgesamt
erhalt man als Boson-Vertauschungsregeln:
bk byk , byk bk = kk
(3.21)
bk bk , bk bk = 0
byk byk , byk byk = 0:
0
0
0
0
0
0
0
28
3.4 Observable
Wie in Kap. 2 beweist man, da ein Einteilchen-Operator f in der Teilchenzahl-Darstellung
die Form hat
X
f^ = (mjf jn) bym bn;
(3.22)
m;n
entsprechend gilt fur einen Zweiteilchen-Operator g in Teilchenzahl-Darstellung
X
(pqjgjmn) bypbyq bnbm :
(3.23)
g^ = 21
p;q;m;n
f^ und g^ haben formal die gleiche Struktur fur Bosonen und Fermionen; der Unterschied
liegt nur in den Vertauschungsregeln der Erzeugungs- und Vernichtungs-Operatoren und
den Zustanden, auf die f^ bzw. g^ wirken.
3.5 Anwendungsbeispiele
Die folgenden Beispiele sollen noch einmal konkret den Unterschied Fermionen - Bosonen
deutlich machen.
1. Grundzustand und einfache angeregte Zustande in N -Bosonen-Systemen.
Im Grundzustand eines Systems von N unabhangigen Bosonen benden sich alle N
Teilchen im niedrigsten Einteilchen-Niveau:
Einfache angeregte Zustande erhalt man, indem man ein (oder mehrere) Teilchen in ein
hoheres Niveau setzt, z:B:
2. Grundzustands-Erwartungswerte
29
Fur die kinetische Energie (oder andere Einteilchen-Operatoren) erhalt man
X
< 0 jT^j0 >= (mjtjn) < 0 jbym bnj0 >= N t0;
(3.24)
m;n
wo t0 die kinetische Energie eines Teilchens im tiefsten Einteilchen-Zustand '0 ist.
Fur die potentielle Energie (oder andere Zweiteilchen-Operatoren) wird
X
< 0 jV^ j0 >= 21
(kljV jmn) < 0 jbyk byl bnbm j0 >= 1 N (N , 1)V0
(3.25)
2
m;n;k;l
mit
Erganzung zu 3.3.2:
V0 =
Z Z
d d 0j'0( )j2V (; 0)j'0( 0)j2:
(3.26)
Die Eigenwerte zu N^k = byk bk sind reell, da N^k hermitisch. Sie sind uberdies nichtnegativ, denn
< :::nk :::jbyk bk j:::nk ::: >=
=
X
X
ni
ni
< :::nk :::jbyk j:::n0i :: >< :::n0i :::jbk j:::nk ::: >
(3.27)
0
j < :::n0i :::jbk j:::nk ::: > j2 0:
0
Die formalen Eigenschaften von N^k bzw. N^ sind also konsistent mit der physikalischen
Interpretation.
30
Kapitel 4
Quantisierung des Strahlungsfeldes:
Photonen
Bei der Entstehung der Quantentheorie spielte die elektromagnetische Strahlung (Planck'sche Strahlungsformel) eine wesentliche Rolle. Die von Planck implizit benutzte Beschreibung des Strahlungsfeldes durch Photonen werden wir nach Quantisierung im Rahmen der Teilchenzahl-Darstellung durchfuhren. Die Ergebnisse werden wir in Teil III
benutzen, um die statistischen Eigenschaften des Photonen-Gases zu behandeln.
4.1 Energie des klassischen Strahlungsfeldes
In Coulomb-Eichung (vgl. Elektrodynamik)
r A(r; t) = 0
(4.1)
beschreibt das aus der Wellengleichung
2
A(r; t) , 12 @ 2 A(r; t) = 0
(4.2)
c @t
zu berechnende Vektorpotential A(r; t) das freie Strahlungsfeld vollstandig. Mit dem Separationsansatz
A(r; t) = U(r)v(t)
(4.3)
geht (4.2) uber in
U + k2 U = 0
(4.4)
und
@2 v + !2v = 0
(4.5)
@t2
mit
2
k2 = !c2
(4.6)
als Separations-Konstante. Spezielle Losungen sind ebene Wellen
A(r; t) expfi(k r , !t)g;
31
(4.7)
aus denen durch Superposition bzgl. k die allgemeine Losung aufgebaut werden kann.
Denken wir uns das Strahlungsfeld in ein sehr groes, aber endliches Normierungsvolumen
V eingeschlossen, so erhalten wir die allgemeine Losung in Form einer Fourier-Reihe:
A(r; t) =
Dabei ist
v
u
Xu
t
;j
4c2 b (t) e expfik rg:
V ! ;j j
k = 2L (1; 2; 3); i ganze Zahl; V = L3
der Wellenvektor und
(4.8)
(4.9)
ej ; j = 1; 2
(4.10)
sind reelle Polarisations-Vektoren, welche senkrecht zueinander und, wegen der Transversalitat des Lichts, senkrecht zu k stehen. Die Darstellung (4.8) fur A ist reell, wenn man
verlangt
b;j = b,;j :
(4.11)
Wir wollen nun { im Hinblick auf die beabsichtigte Quantisierung des Strahlungsfeldes {
die Energie des Feldes berechnen, ausgehend von der bekannten Formel
Z
(4.12)
Hr;kl: = 81 d [E 2 + B 2 ] mit 41 = 0 :
Mit
B = r A; E = , 1c @t@ A
(4.13)
wird daraus
Z
@ A)2 + (r A)2]:
Hr;kl: = 81 d [ c12 ( @t
(4.14)
Setzt man (4.8) ein, so wird schlielich
X
Hr;kl: = 21 ! (b;j b;j + b;j b;j );
(4.15)
;j
wenn man beachtet, da
Z
(4.16)
d expfi[k + k ] rg = 0
auer fur k = ,k . Wie fur ein abgeschlossenes System zu erwarten, ist Hr;kl: unabhangig
von der Zeit, denn die b;j befolgen die Dierentialgleichungen
0
0
mit den Basislosungen
@2 b + !2b = 0
;j
@t2 ;j
(4.17)
b;j = expfi!tg:
(4.18)
32
4.2 Quantisierung
Fur die Quantisierung bemerken wir, da die klassische Energie gema (4.15) und (4.17)
sich additiv aus den Beitragen einzelner, durch die Amplituden b;j (t) beschriebener Oszillatoren zusammensetzt. Das gleiche gilt fur Impuls oder Drehimpuls des Feldes. Die
Quantisierung des harmonischen Oszillators ist bekannt (Quantentheorie): wir ersetzen die klassischen Amplituden b;j und b;j durch Operatoren b;j und by;j mit der
Vertauschungsregel
[b;j ; by ;j ] = h jj
(4.19)
fur t = t0 , alle ubrigen Kommutatoren sollen verschwinden. Zweckmaigerweise substituiert man noch
p
b;j = h ~b;j ;
(4.20)
so da der Kommutator (4.19) bei gleichen Zeiten ubergeht in
[~b;j ; ~by ;j ] = jj :
(4.21)
Von nun ab benutzen wir nur die Operatoren ~bj und ~byj , schreiben der Einfachheit halber
jedoch bj ~bj . Der Hamilton-Operator des Strahlungsfeldes lautet dann
X
X
Hr = 21 (b;j by;j + by;j b;j )h! = h !(by;j b;j + 12 ):
(4.22)
;j
;j
0
0
0
0
0
0
0
0
Das Strahlungsfeld kann also wie ein System entkoppelter harmonischer Oszillatoren behandelt werden. Vergleicht man (4.21) mit (3.21), so sieht man, da es sich um Bosonen
handelt. Diese Bosonen { Photonen { sind charakterisiert durch ihren Impuls h k , Energie h ! und Polarisationszustand j . In (4.22) ist
N^;j = by;j b;j
(4.23)
der Teilchenzahl-Operator fur den Schwingungstyp (; j ), dessen Eigenwerte angeben,
wieviel Photonen der Sorte (; j ) vorhanden sind; dazu tritt in jedem Schwingungstyp
eine Nullpunkt-Energie von 1=2h!. Die Eigenzustande zu Hr sind charakterisiert durch
Angabe der Zahl der Photonen der Sorte (; j ) :
X
Hr j:::n;j :: >= h ! n;j j:::n;j ::: > :
(4.24)
;j
nach Abzug der Nullpunktsenergie.
Bemerkungen:
1. Die klassische Energie in (4.15) hatten wir absichtlich symmetrisch in b, b geschrie-
ben, um den U bergang zum Hamilton-Operator eindeutig zu machen (vgl. hierzu auch:
Quantentheorie).
2. Anstelle der ebenen Wellen hatte man als Basislosungen von (4.2) auch Kugelwellen
benutzen konnen. Nach Quantisierung ware man dann zu Photonen gelangt, die auer
durch Energie und Polarisation durch ihren Drehimpuls gekennzeichnet sind. Den U bergang zwischen den beiden Darstellungen vermittelt die Entwicklung der ebenen Welle nach
33
Kugelfunktionen (vgl. Quantentheorie oder Elektrodynamik). Die Situation ist analog zum
Fall freier, materieller Teilchen (also Ruhemasse 6= 0), wo man je nach Problemstellung
die Impuls (ebene Welle)- oder Drehimpuls (Kugelwelle)-Klassikation benutzen kann.
Die Drehimpuls-Klassikation von Photonen ndet bei Strahlungsproblemen von Atomen
oder Atomkernen Anwendung, da Atom- und Kern-Zustande durch scharfen Drehimpuls
gekennzeichnet sind; in der Festkorperphysik ist die Impuls-Klassikation aus Grunden
der Geometrie angemessen.
3. Auer den oben eingefuhrten transversalen Photonen (transversal, da stets ej k =
0) gibt es noch longitudinale Photonen, welche man zur Beschreibung der CoulombWechselwirkung verwenden kann (Analogie: Erklarung der Kernkrafte durch Austausch
von Mesonen). Sie entsprechen einer Fourier-Zerlegung des skalaren Potentials , welches die Wechselwirkung in statischen Ladungsverteilungen erfat. Da uns oben nur das
Strahlungsfeld interessierte, haben wir 0 normiert; bei der Beschreibung der Wechselwirkung von Strahlung und Materie mussen wir die Coulomb-Energie dann als Beitrag
zur Energie der geladenen Teilchen behandeln.
4.3 Wechselwirkung von Strahlungsfeld und Materie
Der Hamilton-Operator eines Systems identischer Teilchen { die Verallgemeinerung auf
nicht-identische Teilchen erfordert nur die Indizierung von Masse, Ladung und magnetischem Moment { mit Masse m, Ladung e und magnetischen Moment lautet, bei
Anwesenheit des Strahlungsfeldes, inklusive der Feldenergie
N
N
X
X
X
(4.25)
H = 21m (pi , ec A(ri))2 + 12 Vij , (~i [r A(ri)]) + Hr :
i=1
i=1
i6=j
In Hinblick auf eine Storungsrechnung trennen wir auf
H = Hp + Hr + H 0;
(4.26)
wo Hr das freie Strahlungsfeld gema (4.22) beschreibt, Hp der Hamiltonoperator der
Teilchen bei Abwesenheit des A-Feldes ist
X
X
Hp = 21m p2i + 12 Vij ;
(4.27)
i
i6=j
und H 0 die Wechselwirkung zwischen Teilchen und Photonen beschreibt. In H 0 ist A(ri)
ein Operator:
s
X
A(ri) =
h c V 4h! ej fb;j exp(ik ri) + by;j exp(,ik ri)g;
(4.28)
>0;j
der in linearer Form Photon-Erzeugungs- wie Vernichtungsoperatoren enthalt. Im Einzelnen zerfallt H 0 in 3 Anteile:
i) einen uber die Ladung der Teilchen angreifenden Beitrag,
e X (p A(r ) + A(r ) p );
, 2mc
(4.29)
i
i
i
i
i
34
der die Operatoren b;j und by;j linear enthalt, also Prozesse ermoglicht, bei denen in
niedrigster Naherung 1 Photon erzeugt oder vernichtet wird.
ii) einen uber das magnetische Moment wirkenden Anteil,
,
X
i
(~i [r A(ri)]);
(4.30)
der bzgl. b;j und by;j den gleichen Aufbau wie i) hat,
iii) einen in b, by quadratischen Term,
e2
2mc2
X
i
A(ri) A(ri);
(4.31)
der in niedrigster Naherung zwei-Photonen-Prozesse ermoglicht.
4.4 Die 0. Naherung
Die Eigenfunktionen zu
H0 = Hp + Hr
wollen wir im folgenden als bekannt voraussetzen,
H0j; nj >= (E +
X
;j
nj h ! )j; nj > :
(4.32)
(4.33)
Dabei charakterisiert die (als zumindest approximativ bekannt angenommenen) Eigenzustande zu Hp mit der Energie E , z:B . die Eigenzustande des H -Atoms.
Bezogen auf (4.32), (4.33) als 0. Naherung werden wir nun versuchen, den Einu von
0
H im Rahmen einer Storungsrechnung zu erfassen.
4.5 Absorption und Emission von Photonen
Unter der Wirkung von H 0 konnen (siehe unter 4.3) Photonen erzeugt (vernichtet) werden.
Wegen der Erhaltungssatze fur das abgeschlossene System (Materie + Strahlungsfeld) mu
die vom Strahlungsfeld aufgenommene (abgegebene) Energie (ebenso Impuls, Drehimpuls)
von der Materie (z:B . Atomen, Molekulen) abgegeben (aufgenommen) werden. Bei der
Absorption von Photonen geht die Materie in einen angeregten Zustand uber:
35
umgekehrt kann die Materie aus einem angeregten Zustand unter Photonenemission in
einen tieferen Zustand (z.B. den Grundzustand) ubergehen.
Quantitativ mussen wir nun die Wahrscheinlichkeit dafur berechnen, da das durch H0
beschriebene, nicht wechselwirkende System vermoge der Wechselwirkung H 0 aus einem
Anfangszustand j; nj > in einen Endzustand j0; n0j > ubergeht. Dazu verwenden wir
die Zeitentwicklung eines Systems im Dirac-Bild.
Zur Zeit t = 0 liege das System im Zustand j; nj > vor; die Zeitentwicklung erfolgt
im Dirac-Bild gema
jD (t) >= UD (t; 0)j; nj >
(4.34)
mit
Z t
(4.35)
UD (t; 0) = 1 , hi dt0 HD0 (t0)UD (t0 ; 0);
0
wobei
(4.36)
HD0 (t0) = exp( hi H0t0 )H 0 exp(, hi H0 t0):
Der Operator H 0 ist im Schrodinger-Bild fur das betrachtete abgeschlossene System zeitunabhangig. Die Amplitude, mit der der gesuchte Endzustand j0; n0j > in jD (t) >
enthalten ist, wird
< 0; n0j jUD (t; 0)j; nj >;
(4.37)
ihr Betragsquadrat ergibt die Wahrscheinlichkeit, zur Zeit t das System in j0; n0j > als
Endzustand zu nden.
Wenn wir uns auf den einfachsten Proze { Absorption bzw. Emission von einem
Photon { beschranken, konnen wir fur UD (t; 0) die Naherung benutzen:
Z t
i
UD (t; 0) 1 , h dt0 HD0 (t0);
(4.38)
0
dabei tragt der 1-Term wegen der Orthogonalitat der j; nj > zur U bergangswahrscheinlichkeit nicht bei. Es bleibt also zu berechnen
Z t
Z t
0
0
0
0
0
0
0
0
dt < ; nj jHD (t )j; nj >=< ; nj jH j; nj > dt0 exp( hi t0[E 0 , E ]); (4.39)
0
0
wobei fur H 0 (4.29) und (4.30) einzusetzen sind; weiter ist abgekurzt
E = E +
X
;j
36
nj h !;
(4.40)
E 0 = E +
0
Die Zeitintegration in (4.39) ergibt
X
;j
n0j h !:
i
0
,ih exp( h tE[E0 ,,EE ]) , 1 :
(4.41)
W (t) = h ,2( sin(t ) )2 j < 0 ; n0j jH 0j; nj > j2
(4.42)
Fur die Wahrscheinlichkeit W (t), da das System nach der Zeit t aus dem Anfangszustand
j; nj > in den Endzustand j0; n0j > ubergegangen ist, erhalt man also
mit
0,E
= E 2
(4.43)
h :
Die Funktion (sin(t )= )2 hat die unten skizzierte Form; das Hauptmaximum bei = 0
wird mit wachsendem t immer scharfer, die Nebenmaxima werden abgebaut.
U bergange sind dann besonders wahrscheinlich, wenn
E 0 E:
(4.44)
Der Faktor (sin(t )= )2 in (4.42) beinhaltet also die Energieerhaltung im Rahmen der
Energie-Zeit-Unscharfe (vgl. Quantentheorie). Fur t ! 1 ist die Energieerhaltung streng
erfullt, d:h:E 0 = E:
Das Matrixelement < 0; n0j jH 0j; nj > aus (4.42) spaltet auf in Anteile, die nur die
Materie betreen, und solche, die nur die Strahlung betreen. Bei Beschrankung auf 1
37
- Photonen - Prozesse tragen aus H 0 nur die Terme (4.29) (4.30) bei. Die elektrischen
U bergange werden bestimmt durch
< 0 j
durch
X
l
pl exp(ik rl )j >;
< 0j (~i k) exp(ik ri)j >
X
i
(4.45)
(4.46)
die magnetischen U bergange. Eine Entwicklung der ebenen Welle nach Kugelfunktionen
liefert Dipol-Strahlung, Quadrupol-Strahlung etc. Zu (4.45) und (4.46) treten jeweils die
das Strahlungsfeld betreenden Anteile
< n0j jbj jnj >
(4.47)
< n0j jbyj jnj > :
Im Fall der Absorption von Strahlung wird
(4.48)
bzw.
j < nj , 1jbj jnj > j2 = nj :
(4.49)
Die Absorptionswahrscheinlichkeit ist also proportional zur Zahl der anfangs vorhandenen Photonen bzw. der Intensitat des Feldes. Die Emissionswahrscheinlichkeit
ist
j < nj + 1jbyj jnj > j2 = nj + 1:
(4.50)
An diesem Resultat ist bemerkenswert, da auch dann Photonen-Emission stattndet,
wenn im Anfangszustand nj = 0 ist: spontane Emission (im Gegensatz zu der mit
nj wachsenden induzierten Emission). Auf Grund dieser spontanen Emission sind alle
angeregten Zustande atomarer Systeme instabil, sie haben eine naturliche Linienbreite.
Die Tatsache, da atomare Systeme auf Grund der elektromagnetischen Wechselwirkung aus angeregten Zustanden spontan unter Photonenemission in den Grundzustand
ubergehen, ist im Rahmen der klassischen Physik unverstandlich. Klassisch ist der Grundzustand des Strahlungsfeldes dadurch gekennzeichnet, da
Ekl: = ~kl: 0:
(4.51)
Wo aber kein elektromagnetisches Feld vorhanden ist, kann es aber auch keine elektromagnetische Wechselwirkung mit Materie geben. Anders die Situation nach Quantisierung
des Strahlungsfeldes: der Grundzustand ist das Photonenvakuum j0 >; in diesem Zustand
ist zwar der Erwartungswert der Feldoperatoren A, E und B 0,
< 0jAj0 >=< 0jEj0 >=< 0jBj0 >= 0;
(4.52)
es bleiben aber von null verschiedene mittlere, quadratische Schwankungen (VakuumsFluktuationen), z:B:
(E)2 = (< 0jE2j0 > , < 0jEj0 >2) 6= 0;
38
(4.53)
da der Teilchenzahloperator N^j = byj bj mit den in den bj bzw. byj linearen Feldoperatoren nicht vertauscht:
[N^j ; byj ] = byj ; [N^j ; bj ] = ,bj :
(4.54)
Die Energie des Strahlungsfeldes (bzw. Teilchenzahl) und Feldstarken sind nicht simultan
scharf!
Auf Absorption und Emission von Photonen, insbesondere die spontane Emission,
werden wir in Teil III bei der Behandlung des Photonen-Gases zuruckkommen, wenn wir
die Planck'sche Strahlungsformel besprechen.
39
Teil II
Grundlagen der statistischen Physik
40
Kapitel 5
Konzept der statistischen
Gesamtheit
5.1 Mikro- und Makrozustande
Ein System N identischer Teilchen ist vollstandig beschrieben, wenn seine Wellenfunktion
(1:::N ; t) bekannt ist; in der klassischen Physik geben die Koordinaten qi(t) und Impulse pi (t) eine vollstandige Beschreibung. Einen solchen vollstandig determinierten Zustand
wollen wir im folgenden Mikrozustand nennen. Er beschreibt im Rahmen der Quantentheorie eine reine Gesamtheit (vgl. Quantentheorie). Fur makroskopische Dimensionen
(N 1023) ist eine solche vollstandige Beschreibung in der Praxis unmoglich. Ein makroskopisches System konnen wir praktisch nur durch makroskopische Megroen wie
Gesamtenergie E , Volumen V , Temperatur T etc. charakterisieren. Einen solchen durch
einige wenige makroskopische Groen bestimmten Zustand nennen wir Makrozustand.
Derselbe Makrozustand kann im allgemeinen durch eine groe Anzahl von Mikrozustanden realisiert werden. Beispiele: fur drei unabhangige, gleichartige Oszillatoren
kann ein Zustand mit vorgegebener Gesamtenergie E = h !(3=2 + 3) = 9=2h! auf verschiedene Weise realisiert werden:
oder: drei Teilchen mit Spin 1=2 seien an verschiedenen Raumpunkten lokalisiert (paramagnetischer Kristall); je nach Spinstellung ~ relativ zur Richtung eines aueren Magnet41
feldes sei das magnetische Moment +(,). Der Zustand mit Gesamtmoment , kann
auf folgende verschiedene Arten realisiert werden:
Oensichtlich nimmt die Zahl der Realisierungsmoglichkeiten mit wachsendem N zu.
Um die makroskopischen Eigenschaften eines Systems vieler identischer Teilchen zu bestimmen, geht man in der statistischen Mechanik nun wie folgt vor: Anstelle des tatsachlich
vorhandenen Systems (z:B . ein Gas mit N Molekulen), von dem man bestimmte makroskopische Eigenschaften (z:B . die spezische Warme) berechnen mochte, betrachtet man
eine groe Anzahl von gedachten Kopien dieses Systems, welche sich in all den Mikrozustanden benden konnen, die mit bestimmten makroskopisch vorgegebenen Bedingungen (z:B . konstante Gesamtenergie fur ein abgeschlossenes System) vertraglich sind. Eine
solche statistische Gesamtheit ist charakterisiert durch die Verteilung der einzelnen
Systeme auf die moglichen Mikrozustande. In der Quantentheorie benutzt man den statistischen Operator (auch die Bezeichnung Dichteoperator ist gebrauchlich) (vgl.
Quantentheorie), klassisch die Dichtefunktion kl: im 6N-dimensionalen Phasenraum, um
eine statistische Gesamtheit zu beschreiben.
Kennt man bzw. kl:, so berechnet man makroskopische Eigenschaften des tatsachlichen Systems durch Mittelwertbildung uber die statistische Gesamtheit. Als Ma dafur,
wie verlalich solche Mittelwerte sind, kann man die mittleren quadratischen Schwankungen betrachten. Es wird sich zeigen, da diese mit wachsender Teilchenzahl N abnehmen.
Bemerkung: Die N Teilchen eines Systems konnen miteinander wechselwirken (z:B . die
Atome oder Molekule eines realen Gases) oder auch nicht (ideales Gas). Dagegen impliziert
das Konzept der statistischen Gesamtheit, da die einzelnen Systeme der Gesamtheit sich
stets unabhangig voneinander bewegen.
5.2 Der statistische Operator
Wenn jm > die moglichen Mikrozustande sind und pm die relativen Wahrscheinlichkeiten
dafur, da sich Systeme der Gesamtheit im Zustand jm > benden, so lat sich der
statistische Operator schreiben als (vgl. Quantentheorie)
=
X
m
pmjm >< m j mit
X
m
pm = 1:
(5.1)
Im Schrodinger-Bild ist jm > und damit zeitabhangig. Schreiben wir die Zeitentwicklung von jm > als
jm(t) >= U (t; t0 )jm(t0 ) >;
(5.2)
so wird (Quantentheorie)
(t) = U (t; t0 )(t0)U y (t; t0)
(5.3)
42
oder nach Dierentiation bzgl. t
@ = [H; ]:
ih @t
(5.4)
Wichtige Spezialfalle:
1. Reine Gesamtheiten Wenn
= jm >< m j;
(5.5)
so liegt eine reine Gesamtheit vor; man besitzt die maximal mogliche Information uber
das System. Alle Systeme der Gesamtheit benden sich mit Sicherheit im Zustand jm > :
Aus (5.5) folgt
2 = (5.6)
fur reine Gesamtheiten. Umgekehrt ist durch (5.6) eine reine Gesamtheit charakterisiert,
wenn - wie ublicherweise angenommen - so normiert ist, da (vgl. (5.1))
Spfg = 1; d:h: pm = 1:
(5.7)
X
m
2. Statistisches Gleichgewicht
Von besonderem Interesse in der statistischen Mechanik ist der Fall des statistischen
Gleichgewichts, deniert durch
@ = 0:
(5.8)
@t
Er kann auf zweierlei Weise realisiert werden, namlich durch
= 0 1
(5.9)
oder durch
= (Q)
(5.10)
wenn Q eine Erhaltungsgroe ist; speziell also
= (H ):
(5.11)
Mit (5.4 folgt aus (5.9) bzw. (5.10) sofort (5.8). Bei der Besprechung der praktisch wichtigen Gleichgewichts-Gesamtheiten werden wir auf (5.9) bzw. (5.10) zuruckkommen.
5.3 Statistische Mittelwerte
Kennt man den statistischen Operator fur ein System unter bestimmten makroskopischen Bedingungen (z:B . feste Teilchenzahl, konstanter Druck, ...), so berechnet sich der
Mittelwert einer Observablen A uber die statistische Gesamtheit als
X
X
< A >= SpfAg = < ijm >< m jAji > pm = impm < m jAji > (5.12)
i;m
i;m
43
=
X
m
pm < m jAjm >= SpfAg:
Gleichung (5.12) zeigt, da in die Berechnung von < A > auer der statistischen Mittelwertbildung
X
< A >= pmAm
(5.13)
m
mit
Am =< m jAjm >
(5.14)
noch eine quantenmechanische Mittelwertbildung in Form des Erwartungswertes (5.14)
eingeht.
Um den Unterschied deutlich zu machen, vergleichen wir den statistischen Mittelwert
(5.13) fur die durch (5.1) beschriebene statistische Gesamtheit mit dem Erwartungswert
von A in dem reinen Zustand
jm (t) >=
namlich
< jAj >=
vorausgesetzt, da j > normiert ist:
X
X
m;n
X
m
m
cm (t)jm >;
cm cn < m jAjn >;
jcmj2 = 1
(5.15)
(5.16)
(5.17)
bei orthonormierten Zustanden m . Im Gegensatz zu (5.13), wo die pm als Wahrscheinlichkeiten reelle, positive Zahlen sind, sind die Koezienten in (5.16) im allgemeinen komplex;
sie hangen von den Phasen der Koezienten cm (t) ab. - Der Erwartungswert < jAj >
der Observablen A ist insgesamt naturlich reell! - Nur wenn die jm > Eigenzustande zu
A sind
Ajm >= am jm >;
(5.18)
erhalt (5.16) die Form eines statistischen Mittelwertes
< jAj >=
X
m
jcmj2am :
(5.19)
Die Form (5.19) fur den Erwartungswert einer Observablen A ist Ansatzpunkt zur statistischen Interpretation der Quantenmechanik (vgl. Quantentheorie).
Um Miverstandnisse zu vermeiden, sei nochmals betont: eine statistische (oder gemischte) Gesamtheit wird beschrieben durch die reellen Zahlen pm , welche die Wahrscheinlichkeiten dafur angeben, da in der Gesamtheit der Zustand jm > realisiert ist;
dagegen wird ein reiner Zustand j > charakterisiert durch seine komplexen Entwicklungskoezienten cm (t) in einer orthonormierten Basis jm > : Wahrend in einem
reinen Zustand auf Grund fester Phasenbeziehungen (gegeben durch die komplexen Zahlen cm(t)) Interferenz zwischen den jm > moglich ist (vgl. (5.16)!), ist dies fur eine
gemischte Gesamtheit nicht moglich, wie Gleichung (5.12) zeigt.
44
 berlaMit anderen Worten: eine statistische Gesamtheit wird durch eine inkoharente U
gerung von Zustanden beschrieben, eine reine Gesamtheit durch eine koharente U berlagerung.
Der statistische Mittelwert < A > mu naturlich unabhangig davon sein, in welcher
Basis die Spur-Bildung erfolgt. Dies ist in der Tat der Fall: wir entwickeln ji > in einer
vollstandigen orthonormierten Basis j >;
X
ji >= ai j >;
(5.20)
und nden wegen der Unitaritat der Matrix ai ,
X
XX
< ijAji >=
ai ai < jAj >
i i
=
X
< jAj >=
X
(5.21)
< jAj > :
Fur die in (5.8) denierten stationaren Gesamtheiten sind die statistischen Mittelwerte
(wie zu erwarten) unabhangig von der Zeit t, denn hangt nach (5.8) im statistischen
Gleichgewicht nicht von t ab. Observable sind im Schrodinger-Bild zeitunabhangig, und
die Spur-Bildung konnen wir uns in der Basis der stationaren Zustande zum HamiltonOperator H des Systems ausgefuhrt denken.
5.4 Die klassische Dichtefunktion kl
Wir wollen im folgenden kurz die klassische Beschreibung einer statistischen Gesamtheit
skizzieren und die Analogie zur Quantenstatistik deutlich machen.
Ein klassisches mechanisches System ist vollstandig beschrieben durch die Angabe der
Orts- und Impuls-Koordinaten der Teilchen als Funktion der Zeit,
fqi(t); pi(t)g; i = 1; :::; 3N:
(5.22)
In dem 6N - dimensionalen Raum der Koordinaten qi, pi wird das N -Teilchen-System zu
jedem Zeitpunkt t durch einen Punkt dargestellt; man nennt diesen Raum den Phasenraum. Im Laufe der Zeit bewegt sich der das System charakterisierende Phasenpunkt
gema den Bewegungsgleichungen
(5.23)
p_i = , @q@ Hkl:; q_i = @p@ Hkl:
i
i
mit Hkl: = Hkl:(qi ; pi) als Hamilton-Funktion, auf einer Trajektorie durch den Phasenraum, siehe Skizze.
Eine statistische Gesamtheit von Systemen beschreiben wir dann durch eine Dichtefunktion kl: = kl:(qi; pi; t) im Phasenraum, welche die Wahrscheinlichkeit angibt, zur Zeit t
ein System der Gesamtheit im Phasenpunkt fqi, pi g anzutreen.
Da die Zahl M der Systeme der Gesamtheit fest ist, konnen wir kl: so normieren, da
Z
Y
i
dqidpi kl:(qi; pi; t) = 1:
45
(5.24)
Trajektorie im Phasenraum; P (t) Zustand des betrachteten Systems zur Zeit t.
Momentaufnahme einer Gesamtheit vom Systemen im Phasenraum.
Wir untersuchen nun das Zeitverhalten von kl:. Da die Gesamtzahl der Systeme der Gesamtheit fest ist, ist die Zahl der Phasenpunkte, die ein bestimmtes Volumen im Phasenraum pro Sekunde verlassen, gleich der Abnahme der Phasenpunkte in diesem Volumen.
Diesen Erhaltungssatz fassen wir (etwa in Analogie zur Ladungserhaltung im R3 ) in
Form einer Kontinuitatsgleichung in 6N Dimensionen
@ + div( v ) = 0
(5.25)
kl: kl:
@t kl:
mit
vkl: =: (q_i; p_i);
(5.26)
div =: ( @q@ ; @p@ ):
(5.27)
i
i
Gleichung (5.25) lat sich in eine kompakte Form bringen, welche die Analogie zwischen
klassischer Verteilungsfunktion kl: und statistischem Operator deutlich macht. Dazu
46
formen wir um
N
( @q@ (kl:q_i) + @p@ (kl:p_i))
3
X
div(kl:vkl:) =
i=1
i
i
(5.28)
X
( @kl: q_i + @kl: p_i) + kl:( @ p_i + @ q_i )
@pi
@pi @qi
i @qi
i
und beachten, da der letzte Term in (5.28) vermoge der Bewegungsgleichungen verschwindet. Gleichung (5.25) lautet dann
@ + X @kl: q_ + X @kl: p_ = 0;
(5.29)
@t kl: i @qi i i @pi i
=
X
woraus mit Hilfe von (5.23) und der Denition der Poisson-Klammern folgt:
@ = fH ; g:
(5.30)
kl: kl:
@t kl:
Gleichung (5.30) entspricht Gleichung (5.4) und lauft unter dem Namen Liouville-Gleichung; im Hinblick auf (5.29) ndet man haug auch die Formulierung
d = 0:
(5.31)
dt kl:
Eine klassische statistische Gesamtheit bendet sich im statistischen Gleichgewicht, wenn
@ = 0:
(5.32)
@t kl:
Dieser Fall ist auf zweierlei Weise realisierbar, namlich durch
kl:(qi; pi; t) = const:
(5.33)
oder durch
kl: = kl:(Qkl:);
(5.34)
wenn Qkl: eine Erhaltungsgroe ist. Im Falle von (5.33) ist trivialerweise (5.32) erfullt; im
Fall (5.34) folgt zunachst aus der Eigenschaft von Qkl: als Erhaltungsgroe
d Q = ( @Qkl: q_ + @Qkl: p_ ) = 0:
(5.35)
dt kl: i @qi i @pi i
Aus (5.34) ergibt sich dann zusammen mit (5.31):
@ = , dkl: ( @Qkl: q_ + @Qkl: p_ ) = 0; q:e:d:
(5.36)
@t kl:
dQkl: i @qi i @pi i
Mit der Normierung (5.24) erhalten wir fur eine Observable Akl: als Mittelwert uber die
durch kl: beschriebene Gesamtheit
X
X
< Akl: >=
Z
Y
i
dqidpi kl:(qi ; pi; t)Akl:(qi ; pi):
47
(5.37)
5.5 Zusammenfassung
Als fundamentale Aufgaben der statistischen Mechanik ergeben sich:
1. Bestimmung von bzw. kl: in Abhangigkeit von dem betrachteten System unter
den jeweiligen makroskopischen Bedingungen. Auf diesen Punkt werden wir fur den Fall
des statistischen Gleichgewichts in Kap. 7. eingehen.
2. Berechnung makroskopischer Eigenschaften bei bekanntem bzw. kl::
Fur Groen, denen in der Quantentheorie eine Observable korrespondiert, dargestellt
durch einen selbstadjungierten Operator, benutzen wir das Verfahren der Mittelwertbildung aus Kap. 5.3. Die innere Energie U eines Systems z:B . berechnen wir als
U = SpfH g;
wo H der Hamiltonoperator des Systems ist. Ebenso fur die Magnetisierung
< M~ >= Spf~g:
(5.38)
(5.39)
Die zweite Klasse makroskopischer Groen sind Parameter wie Volumen, auere Felder
(hier sind makroskopische, klassische Felder gemeint), raumliche Position des zu untersuchenden makroskopischen Systems etc:; von solchen Parametern nehmen wir an, da
wir sie mit jeder gewunschten Genauigkeit bestimmen konnen. Die beiden wichtigsten Volumen, auere Felder - gehen als Parameter uber die Wellenfunktion in die Theorie
ein; Beispiele: Normierungsvolumen V , Magnetfeld B. Schlielich gibt es im Rahmen
der Thermodynamik Groen, die weder in der klassischen Mechanik noch in der Quantentheorie vorkommen, z:B . Entropie S , Temperatur T .
48
Kapitel 6
Statistische Denition der Entropie
6.1 Entropie als Ma fur fehlende Information
Statistik benutzt man dann, wenn man trotz unvollstandiger Information uber ein System
von makroskopischer Dimension Aussagen uber makroskopische Eigenschaften machen
mochte. Es liegt deshalb nahe, nach einem quantitativen Ma fur Information zu suchen.
U ber einen Gegenstand unseres Interesses (z:B . die Wetterlage) gewinnen wir Information in Form von Nachrichten (Angabe der Windstarke, Lufttemperatur etc.). Je
unwahrscheinlicher eine Nachricht ist, desto groer der Gewinn an Information, wenn
man diese Nachricht tatsachlich empfangt. Insbesondere bringt eine mit Sicherheit zu
erwartende Nachricht (Lufttemperaturen im August in Gieen oberhalb ,300 C ) keine
Information. Wenn die Wahrscheinlichkeit, die Nachricht i zu erhalten, pi ist (0 pi 1),
so mu die Information I ( 0); die wir durch Erhalt der Nachricht i erhalten wurden,
anwachsen, wenn pi abnimmt. In Formeln:
I (pi) = 0 falls pi = 1
(6.1)
und
I (pi) I (p0i) falls pi p0i:
(6.2)
Die konkrete Form der Funktion I (pi) ergibt sich aus der plausiblen Annahme, da die
Information bei voneinander unabhangigen Nachrichten additiv ist. Wenn pi, pj
die Wahrscheinlichkeiten der voneinander unabhangigen Nachrichten i; j sind, so ist die
Wahrscheinlichkeit, beide Nachrichten zu erhalten, das Produkt pipj . Die Additivitat
der Information besagt dann
I (pipj ) = I (pi) + I (pj ):
(6.3)
Losung der Gleichungen (6.1) - (6.3) ist
I (pi) = ,C ln pi
(6.4)
mit C > 0 als einer Konstanten und 0 pi 1:
Nach diesen Vorbemerkungen uber die Grundlagen der Informationstheorie betrachten wir eine statistische Gesamtheit, deren Systeme sich mit den Wahrscheinlichkeiten
49
pi in den Mikrozustanden ji > benden. Wurden wir bei einer vollstandigen Messung
an einem willkurlich herausgegrienen System der Gesamtheit feststellen, da es sich im
Zustand ji > bendet, so ware unser Informationsgewinn proportional ln pi; umgekehrt konnen wir ln pi als ein Ma fur unseren Mangel an Information ansehen, wenn
wir diese Messung nicht durchfuhren (was wir weder praktisch konnen noch wollen, vgl.
Einfuhrung). Die uns bzgl. des betrachteten Systems fehlende Information konnen wir
dann messen durch den statistischen Mittelwert
X
S = ,kB pi ln pi:
(6.5)
i
Die hier eingefuhrte Groe S wird sich als die Entropie des Systems erweisen; kB ist
die Boltzmann-Konstante.
Im Fall einer reinen Gesamtheit im Zustand jm >;
pi = 1 falls i = m; pi = 0 sonst;
(6.6)
wird oensichtlich S = 0. Dies ist vernunftig: wenn wir schon mit Sicherheit wissen, da
das betrachtete System sich im Zustand jm > bendet, so bringt uns die Bestatigung
dieser Tatsache durch eine Messung keinen Informationsgewinn.
Fur die folgenden U berlegungen ist es zweckmaig, S durch den statistischen Operator
auszudrucken. Wir behaupten, da
S = ,kB Spf ln g = ,kB < ln > :
(6.7)
Beweis:
X
X
X
Spf ln g = < ijm >< m j ln ji > pm = pi < ij ln ji >= pi ln pi;
i;m
i
i
(6.8)
da die Zustande ji > Eigenzustande zu mit den Eigenwerten pi sind:
X
ji >= pmjm >< m ji >= piji > :
(6.9)
m
Nach (6.7) ist die Entropie S der statistische Mittelwert des Operators ,kB ln :
6.2 Ein einfaches Beispiel
Drei Teilchen mit Spin 1=2 seien an verschiedenen Raumpunkten lokalisiert; zwischen den
Teilchen besteht keine Wechselwirkung. Je nach der Spinstellung zu einem konstanten,
homogenen Magnetfeld B sei das magnetische Moment eines einzelnen Teilchens .
Insgesamt gibt es 8 Mikrozustande, deren Eigenschaften in der Tabelle kurz zusammengestellt sind:
Zahl der Mikrozustande Gesamt-Moment Gesamt-Energie
1
3
,3B
3
,B
(6.10)
3
,
B
1
,3
3B
50
Wir wollen nun die Entropie des Systems gema (6.5) berechnen fur die folgenden
Falle:
1. Wenn wir uber das System keine weitere Kenntnis besitzen, so sind alle Mikrozustande
gleich wahrscheinlich (Annahme der geringsten Voreingenommenheit). Dann ist
(6.11)
pi = 18 8i;
so da
S = ,kB ln 81 = kB ln 8:
(6.12)
2. Es sei bekannt, da E = B fur das Gesamtsystem ist; dies ist nur durch drei Mikrozustande realisierbar, die ihrerseits wieder gleich wahrscheinlich sind. Also
(6.13)
pi = 31 ; i = 1; 2; 3 ;
so da
S = ,kB ln 31 = kb ln 3:
(6.14)
3. Es sei bekannt, da die Gesamtenergie E = ,3 B ist; diese Situation ist auf nur eine
Weise realisierbar; also besitzen wir vollstandige Kenntnis uber das System. Es wird
S = ,kb ln 1 = 0
(6.15)
wie erwartet.
6.3 Zeitliche A nderung der Entropie
Die Denition von S durch (6.5) zeigt, da S zeitlich konstant ist, da die Zahlen pm (vom
Konzept der statistischen Gesamtheit her) nicht von t abhangen. Wenn wir also S als
Entropie interpretieren wollen, so ist unsere Theorie auf reversible Prozesse bzw. die Beschreibung von Gleichgewichtszustanden beschrankt; irreversible Prozesse sind mit einer
Entropieanderung verbunden. Da wir im Rahmen der bisherigen Theorie irreversible Prozesse nicht erfassen konnen, ist nicht verwunderlich: Die klassischen Bewegungsgleichungen fur ein abgeschlossenes System sind invariant unter Zeitumkehr, d:h. zu jeder Losung
fqi(t), pi(t)g ist auch fqi (,t), ,pi(,t)g eine mogliche Losung der Bewegungsgleichungen;
eine entsprechende Aussage gilt in der Quantentheorie fur die Losungen der SchrodingerGleichung (vgl. Kap. 6.4!). Die Gleichungen (5.4) und (5.30) fur das zeitliche Verhalten
von bzw. kl: sind eine direkte und exakte Konsequenz der Schrodinger-Gleichung bzw.
der Bewegungsgleichungen, so da durch die Einfuhrung des statistischen Operators (5.1) bzw. der Dichtefunktion kl: (5.24) die Zeitumkehr-Invarianz nicht zerstort wird.
Unsere Theorie hat daher fur irreversible Prozesse in der bisherigen Form keinen Platz.
Wir wollen im folgenden andeuten, wie das bisherige Konzept zu erweitern ist, um
irreversible Prozesse erfassen zu konnen. Wenn unsere Identikation von Entropie und
Mangel an Information richtig ist, so mu die erweiterte Theorie die Moglichkeit beinhalten, da im Laufe der Zeit Information verloren geht; dies wurde dann der Moglichkeit
51
einer Entropiezunahme entsprechen. Wir suchen also eine schlechtere Theorie als die
bisherige, die auf dem statistischen Operator aufbaut und ihrerseits schlechter ist als
die exakte Beschreibung eines Systems durch seine Wellenfunktion j(1:::N ; t) > :
Wenn die Kenntnis von fur den Aufbau einer statistischen Begrundung der Thermodynamik zu gut ist, so liegt es nahe, nur noch den Erwartungswert des statistischen
Operators in irgendeiner Basis als bekannt anzusehen. Um diesen Gedanken quantitativ durchzufuhren, wollen wir von der Spektraldarstellung (vgl. Quantentheorie) des
statistischen Operators mit Hilfe der Mikrozustande ji >;
=
X
i
piji >< ij;
(6.16)
ubergehen zu einer Darstellung in einer festen, orthonormierten und vollstandigen Basis
j >; in der dann nicht mehr diagonal ist:
=
X
j >< j:
(6.17)
Die Koezienten sind dann gerade die Matrixelemente von in der Basis j >;
=< jj > :
(6.18)
Wenn wir in der Basis j > nur die Diagonalelemente kennen, so ist dies oensichtlich
weniger Kenntnis als in (6.16) enthalten.
Wir wollen nun das Zeitverhalten der Koezienten untersuchen, die im Gegensatz
zu den pi im allgemeinen von t abhangig sind. Wir greifen zuruck auf (5.4) und bilden
Matrixelemente in der Basis j >:
@ = X(H , H )
ih @t
(6.19)
mit
H =:< jH j > :
Dabei wurde die Vollstandigkeitsrelation
X
j >< j = 1
(6.20)
(6.21)
benutzt. Alternativ konnen wir (5.3) benutzen und nden die formale Losung von (6.19)
(t) =
X
U (t) (0)U (t)
mit
(6.22)
U (t) =:< jU (t; 0)j > :
(6.23)
Da (6.19) und (6.22) exakte Umformungen von (5.3) und (5.4) sind, haben wir gegenuber
(5.3) bzw. (5.4) keine Information verloren; die mit (6.22) berechnete Entropie S ist immer
noch zeitlich konstant.
52
Bemerkung: Es ist generell
( ln ) 6=
X
X
ln (6.24)
mit der Ausnahme, da diagonal in der Basis j > ist.
Wir wollen nun den Fall betrachten, da die statistische Gesamtheit nicht durch die
Eigenwerte pi von , sondern nur durch die Diagonalelemente von in der Basis j >
deniert ist. Es wird sich zeigen, da diese reduzierte Information zeitlich nicht konstant konstant ist, sondern abnimmt. Zur Berechnung der Diagonalelemente hat man zur
Verfugung (vgl. (6.19) bzw. (6.22))
@ = X(H , H )
(6.25)
ih @t
bzw.
X
X
X
(t) = U (t) (0)U (t) = jU j2 (0) + U (t) (0)U (t): (6.26)
6=
Oensichtlich reicht die Kenntnis von (0) als Anfangsinformation nicht aus, um (t)
exakt zu bestimmen. Eine Theorie, die nur mit den Diagonalelementen von arbeiten
will, mu also Approximationen bzgl. der Nichtdiagonal-Elemente machen.
In der statistischen Mechanik wird ad hoc die Annahme gemacht, da auf
Grund statistisch verteilter Phasen sich der Eekt der Nichtdiagonal-Elemente
in (6.25) bzw. (6.26) herausmittelt.
Diese Annahme hat den Charakter eines grundlegenden Postulats und kann nur durch
das Experiment bestatigt oder widerlegt werden. Als Startinformation benutzt man also
die Naherung
(0) = P (0)
(6.27)
und erhalt dann formal P(t) aus
X
P (t) = jU (t)j2P (0):
(6.28)
Die Groen P(t), deren tatsachliche Berechnung ein hier noch unvollstandig gelostes Problem der statistischen Mechanik ist, bestimmen approximativ die Wahrscheinlichkeiten,
die Systeme der statistischen Gesamtheit zur Zeit t in den Zustanden j > zu nden.
Daraus ergibt sich fur die uns fehlende Information
X
S (t) = ,kb P(t) ln P (t):
(6.29)
Sie ist - wie die obigen U berlegungen schon angedeutet haben - zeitabhangig. Wir wollen
unter Ruckgri auf die Naherung (6.28) zeigen, da S (t) in der Tat mit t anwachst. Wir
benutzen dazu die Ungleichung
x ln x , x ln y , x + y 0
(6.30)
53
fur reelle, nicht-negative x; y, welche darauf beruht, da ln x eine monoton anwachsende
Funktion ist. Dann gilt in unserem Problem
P (0) ln P (0) , P (0) ln P (t) , P (0) + P(t) 0:
(6.31)
Gleichung (6.31) multiplizieren wir mit jU (t)j2, summieren uber ; und beachten
X
U = U
(6.32)
als Folge der Unitaritat des Zeitentwicklungs-Operators. Benutzt man im 2. Term von
(6.31) nach Ausfuhrung der o:a. Operationen unsere fundamentale Gleichung (6.28), so
folgt direkt:
X
X
X
X
P (0) ln P (0) , P(t) ln P (t) , P (0) + P(t) 0:
(6.33)
Da auf Grund der Normierung der Wahrscheinlichkeiten P gilt
X
X
P (0) = P (t);
verbleibt
also mit (6.29)
X
P (0) ln P (0) X
P (t) ln P(t);
(6.34)
(6.35)
S (0) S (t):
(6.36)
Damit ist der Rahmen fur die statistische Mechanik irreversibler Prozesse abgesteckt.
Nachdem formal die Moglichkeit der Abnahme von Information (Zunahme von Entropie)
geklart ist, bleibt die Frage nach dem physikalischen Hintergrund. Warum ist unsere
Information in der Praxis so schlecht, da irreversible Prozesse auftreten konnen? Dafur
gibt es die folgenden Grunde:
1. Streng abgeschlossene Systeme sind nicht realisierbar, eine gewisse (wenn auch geringe)
Wechselwirkung W mit der Umgebung ist unvermeidbar. Eine solche Wechselwirkung ist
fur den Fall des thermischen Kontakts sogar notwendig! Da wir diese Wechselwirkung
nie exakt kennen, kennen wir den Hamilton-Operator des Systems nur approximativ; damit sind die Mikrozustande nur approximativ deniert. In der Basis der approximativen
Mikrozustande ist der statistische Operator nicht diagonal. Die Kenntnis der Wahrscheinlichkeitsverteilung - der Systeme der Gesamtheit auf approximative Mikrozustande - zur
Zeit t = 0 geht aber - wie wir oben bewiesen haben - im Laufe der Zeit verloren.
2. Selbst bei vollstandiger Kenntnis des Hamilton-Operators mussen wir davon ausgehen,
da jede Messung mit Ungenauigkeiten behaftet ist, so da wir den statistischen Operator
nie exakt kennen konnen. Neben praktischen Grunden (die wir im Gedankenexperiment
eliminieren konnten) sind dafur fundamentale Prinzipien der Quantentheorie verantwortlich: die Tatsache, da in der Quantentheorie die Meapparatur das Meobjekt beeinut,
und speziell, da die exakte Bestimmung der Energie eines Systems nach der Unscharferelation 1 lange dauern wurde. Dieser aus Meungenauigkeiten folgende Fehler hinsichtlich
der Bestimmung von wachst nach obigen allgemeinen U berlegungen im Laufe der Zeit:
unsere Information verschlechtert sich, d.h. die Entropie wachst.
54
6.4 Zeitumkehr-Invarianz: Mikro-Reversibilitat und
Makro-Irreversibilitat
Zunachst soll die schon erwahnte Mikro-Reversibilitat genauer formuliert werden. Fur
abgeschlossene Systeme sind die Bewegungsgleichungen
invariant unter der Operation
2
mi dtd 2 qi = ,Ki
(6.37)
t ! t0 = ,t:
(6.38)
Wenn also qi (t), pi(t) eine Losung von (6.37) ist, so auch die Kurvenschar qi (,t), ,pi(,t),
welche aus ersterer durch die Operation (6.38) hervorgeht. Anschaulich bedeutet Zeitumkehr, da die Bahnen in entgegengesetzter Richtung durchlaufen werden.
In der Quantentheorie tritt anstelle der Bewegungsgleichungen (6.37) die SchrodingerGleichung
@ ( ::: ; t) = H ( ::: ; t):
ih @t
(6.39)
1
N
1
N
Der Einfachheit halber nehmen wir Teilchen ohne Spin an, so da die Koordinaten i
die Ortskoordinaten der Teilchen bedeuten. Die Korrespondenz zwischen klassischen Observablen und Observablen der Quantentheorie erfordert nun, da bei Zeitumkehr die
Ortskoordinaten ri und die Impulse pi sich gema
ri ! ri; pi ! ,pi
(6.40)
transformieren. Da der Hamilton-Operator H fur ein abgeschlossenes System nur von den
ri und den pi (quadratisch!) abhangt, nicht jedoch von t, ist H invariant unter Zeitumkehr.
Unterziehen wir also die Schrodinger-Gleichung (6.39) der Operation (6.38), so folgt
,ih @t@ 0 (r1:::rN ; t0 ) = H (r1:::rN ; t0);
(6.41)
nach Komplex-Konjugieren
ih @t@ 0 (r1:::rN ; t0) = H (r1:::rN ; t0 )
(6.42)
erhalt man eine Schrodinger-Gleichung fur die Funktionen (r1:::rN ; t0). Also: wenn eine Losung von (6.39) im t-System ist, so ist eine mogliche Losung im t0 -System.
Beispiel: Ebene Welle in +k bzw. ,k Richtung.
Die oben bewiesene Aussage (die analog fur Teilchen mit Spin gultig ist), da zu
jedem Bewegungsablauf, der sich aus den Bewegungsgleichungen bzw. der SchrodingerGleichung ergibt, auch der zeitumgekehrte Bewegungsablauf moglich ist, bezeichnet man
als Mikro-Reversibilitat. Sie scheint auf den ersten Blick im Widerspruch zu stehen
zu der durch Gleichung (6.36) formulierten Makro-Irreversibilitat, durch die ja eine
Zeitrichtung bevorzugt wird. Der scheinbare Widerspruch von Mikro-Reversibilitat und
Makro-Reversibilitat lost sich jedoch, wenn man folgende Punkte beachtet:
55
1. Die Groe S wurde als statistischer Mittelwert eingefuhrt. Die Aussage (6.36) hat
daher nur den Charakter einer Wahrscheinlichkeitsaussage: Die wahrscheinlichste Zeitentwicklung eines makroskopischen Systems ist (bei Abwesenheit auerer Felder) durch
eine Zunahme von S (t) gekennzeichnet; dennoch sind Prozesse moglich, bei denen S (t)
abnimmt, da S statistischen Schwankungen unterworfen ist.
2. Mikro-Reversibilitat ist eine Aussage uber reine Zustande und setzt exakte Kenntnis
des Hamilton-Operators und der Anfangsbedingungen voraus. Makro-Irreversibilitat ist
eine Aussage uber das Verhalten eines Systems, das wir nur unvollstandig kennen und
dessen Eigenschaften wir als Mittelwerte uber eine statistische Gesamtheit erfassen. Beide
Aussagen beziehen sich also auf verschiedene Situationen.
Zur Veranschaulichung der Punkte 1. und 2. sei folgendes Beispiel betrachtet: Gegeben sei ein von seiner Umgebung isolierter Behalter, der durch eine Wand in zwei gleiche
Bereiche unterteilt sei; in der Wand bende sich ein kleines Loch (Skizze),
welches durch einen Schieber verschliebar ist. Die Anfangssituation sei dadurch gekennzeichnet, da sich im Bereich I ein Gas unter dem Druck PI bende, wahrend Bereich
II leer sei. Wenn nun der Schieber geonet wird, gleicht der Druck sich aus, bis sich bei
PI = PII statistisches Gleichgewicht eingestellt hat. Diese Endsituation unterscheidet sich
von der Anfangssituation dadurch, da unsere Information ungenauer geworden ist, die
Entropie gema (6.36) zugenommen hat. Dies schliet nicht aus, da im Verlauf des Druckausgleichs auf Grund statistischer Schwankungen von S kurzzeitig mehr Gasmolekule aus
II zuruck nach I iegen als umgekehrt! - Der Umkehrproze, der von PI = PII 6= 0 ausgehend zu PII = 0, PI 6= 0 fuhrt, ist im Prinzip moglich, allerdings extrem unwahrscheinlich,
da es praktisch unmoglich ist, die Positionen und Impulse der N Gasmolekule - im Sinne
einer Anfangsbedingung zur Losung der Bewegungsgleichungen - so zu adjustieren, da
sich eine Druckdierenz zwischen Bereich I und II aufbaut und im Endzustand Bereich II
leer ist.
Das betrachtete Beispiel zeigt, da das Auftreten von Irreversibilitat eng verknupft
ist mit dem Vorhandensein vieler Teilchen: Zum Beispiel fur N = 2 ist der Proze des
Druckausgleichs ebenso leicht durch Praparieren des Anfangszustandes realisierbar wie
der Umkehrproze.
3. Schlielich ist zu beachten, da die Quantentheorie - ungeachtet der ZeitumkehrInvarianz der Schrodinger-Gleichung - implizit eine Nichtaquivalenz der beiden Zeitrichtungen enthalt. Diese Nichtaquivalenz zeigt sich in Verbindung mit dem fur die Quantentheorie grundlegenden Proze der Wechselwirkung eines quantenmechanischen Systems
(z:B . H -Atom) mit einem klassischen System (z:B . Meapparatur fur Anregungsenergien). Finden zwei solche Prozesse A und B nacheinander statt (Beispiel: Stoe von Gasmolekulen mit den Wanden des Behalters), so sind die beiden Zeitrichtungen nicht mehr
56
Bei wenigen Teilchen ist der Proze des Druckausgleichs ebenso leicht zu praparieren wie
der Umkehrproze.
gleichwertig: Die Behauptung, da die Wahrscheinlichkeit eines bestimmten Resultats des
Prozesses B durch das Ergebnis des Prozesses A mitbestimmt ist, ist nur dann richtig,
wenn A vor B stattndet. Hier liegt vermutlich der Schlussel zu einem tieferen Verstandnis
des Anwachsens der Entropie bei Abwesenheit auerer ordnender Felder.
6.5 Die Postulate der statistischen Mechanik
Das Konzept der statistischen Gesamtheit und die Denition der Entropie (als Mangel an
Information) bieten eine ausreichende Grundlage fur die statistische Mechanik, inklusive
der Moglichkeit, irreversible Prozesse zu beschreiben. Dieser Rahmen gewinnt allerdings
erst dann praktischen Wert, wenn wir fur ein System von N Teilchen zu vorgegebenen
makroskopischen Bedingungen angeben konnen, mit welchen Wahrscheinlichkeiten die
Mitglieder der statistischen Gesamtheit sich auf die Mikrozustande des betrachteten Systems verteilen.
Da die Kenntnis einiger weniger makroskopischer Daten die statistische Gesamtheit im allgemeinen nicht eindeutig festlegt, mussen wir Postulate in die Theorie einbringen, die eine
Bestimmung der oben erwahnten Wahrscheinlichkeiten erlauben. Dabei werden wir versuchen, im Rahmen des Prinzips der geringsten Voreingenommenheit alle zur Verfugung
stehende Information uber das System auszunutzen: The whole truth, and nothing but the
truth. Die uns zur Verfugung stehende makroskopische Information konnen wir in Form
statistischer Mittelwerte erfassen
< Ri >= ri; i = 1; 2; 3; ::; n:
(6.43)
Gleichung (6.43) kann sowohl die Festlegung von Mittelwerten von Observablen bedeuten
als auch ihrer mittleren quadratischen Schwankungen.
Als fundamentale Postulate der statistischen Mechanik fuhren wir nun ein:
Postulat I
Alle Zustande j > einer vollstandigen, orthonormierten Basis haben gleiche
a-priori Wahrscheinlichkeit.
Damit ist gemeint, da die Quantentheorie als solche keine Tendenz hat, gewisse Zustande
(z:B . solche, die energetisch dicht beieinander liegen) gegenuber anderen (solche, die energetisch weniger dicht liegen) zu bevorzugen. Unterschiede in der Wahrscheinlichkeits57
verteilung entstehen erst durch makroskopische Bedingungen, die dem System auferlegt
werden. Speziell hat Postulat I zur Folge, da bei totaler Unkenntnis uber den Zustand des Systems alle Mikrozustande mit gleicher Wahrscheinlichkeit in der Gesamtheit
vertreten sind.
In der klassischen Physik ist Postulat I so zu formulieren, da gleiche Volumina im Phasenraum gleiche a-priori Wahrscheinlichkeiten zukommen.
Da die zur Verfugung stehende makroskopische Information im allgemeinen nicht zur
Bestimmung des statistischen Operators ausreicht, benotigen wir ein Kriterium, welches zwischen verschiedenen 0s, die alle den makroskopischen Bedingungen genugen, eine
Auswahl trit. Als Kriterium benutzen wir die fehlende Information S : Wenn fur zwei
statistische Operatoren 1 6= 2 , welche beide die makroskopischen Bedingungen erfullen,
S1 > S2 gilt, so enthalt 2 zusatzliche Information gegenuber 1 , welche nicht durch Messung gesichert ist. Wir geben daher 1 den Vorzug, um die Theorie so gut wie moglich
von Willkur freizuhalten. Damit ergibt sich
Postulat II:
Dem betrachteten physikalischen System wird der statistische Operator zugeordnet, der den makroskopischen Bedingungen genugt und dabei maximale
fehlende Information reprasentiert.
Postulate I und II wollen wir nun benutzen, um unter verschiedenen makroskopischen
Bedingungen den Fall des statistischen Gleichgewichts zu untersuchen.
58
Kapitel 7
Statistische Gesamtheiten im
Gleichgewicht
7.1 Die uniforme Gesamtheit
Sie ist deniert durch (0 = const.)
= 0 1
(7.1)
oder
= 0
(7.2)
und ist nach Kap. 5.2 im statistischen Gleichgewicht. (7.1) bzw. (7.2) entsprechen dem Fall
totaler Unkenntnis (Unkenntnis bezieht sich auf den Zustand des Systems, nicht auf
die Eigenschaften der Teilchen): alle Zustande sind gleich wahrscheinlich. Oensichtlich
ist
S = const;
(7.3)
totale Unkenntnis kann sich nicht noch verschlechtern. Zum Gluck ist dieser Fall sehr
selten. Hauger liegt vor:
7.2 Die mikrokanonische Gesamtheit
Von einem isolierten System wissen wir, da es scharfe Energie E , festes Volumen V
und scharfe Teilchenzahl N besitzt; die mit E , V und N kompatiblen Mikrozustande
bezeichnen wir mit ji >; i = 1; 2; :::zm. Dann hat der statistische Operator die Form
=
zm
X
i=1
piji >< ij
(7.4)
und es bleibt die Aufgabe, die Koezienten pi zu bestimmen. Dazu benutzen wir das
Prinzip (vgl. Kap. 6.5), da die fehlende Information maximal sein soll. Es mu daher das
Variationsproblem
S = 0
(7.5)
59
unter der Nebenbedingung
Sp() , 1 = 0;
(7.6)
der Normierung von , gelost werden. Gleichungen (7.5) und (7.6) sind aquivalent zu
(S , [Sp() , 1]) = 0;
(7.7)
dabei ist zu variieren bzgl. der pi und ist eine noch zu bestimmende Konstante (LagrangeParameter). Mit aus (7.4) wird
Sp() =
und
Also lautet (7.7):
Die Losung ist
S = ,kB
@ (k
@pj B
X
i
zm
X
pi
(7.8)
pi ln pi:
(7.9)
i=1
zm
X
i=1
pi ln pi + X
i
pi , ) = 0:
ln pj = , , 1 = const:
kB
(7.10)
(7.11)
Die noch freie Groe wird nun so bestimmt, da (7.6) erfullt ist, also:
(7.12)
pj = z1 :
m
Das Ergebnis bedeutet Gleichverteilung auf die moglichen Mikrozustande, im Einklang
mit dem Prinzip gleicher a-priori Wahrscheinlichkeiten (vgl. Kap. 6.5). Fur die Entropie
S erhalt man das Ergebnis
zm 1
X
(7.13)
S = ,kB z ln( z1 ) = kB ln zm :
m
i m
Gleichung (7.13) wird oft als Denition von Entropie benutzt, wobei zm nichts anderes
ist als die Zahl der Realisierungsmoglichkeiten des Makrozustandes. Es sollte jedoch klar
geworden sein, da S aus (7.13) sich auf den Fall des statistischen Gleichgewichts bezieht;
als allgemeine Denition ist (7.13) zu eng, da irreversible Vorgange nicht erfat werden.
Die Groe Zm , deniert durch
Zm =
zm
X
j =1
1 = Sp((E; V; N ));
(7.14)
wird auch mikrokanonische Zustandssumme genannt. In (7.14) bezeichnet (E; V; N )
den Projektor auf den Unterraum von Zustanden, die vorgegebene E , V , N haben. U ber
Zm wird gema (7.13) auch S eine Funktion von E , V , N :
S = S (E; V; N ):
(7.15)
60
Da exakte Energiemessungen auf Grund der Unscharferelation praktisch nicht durchfuhrbar sind, ist es zweckmaig, die Denition der mikrokanonischen Gesamtheit etwas aufzuweichen. Wir ersetzen (7.12) durch
pj = z1 falls E , E < Ej < E + E
(7.16)
m
pj = 0 sonst;
wo zm die Zahl der zwischen E , E und E + E liegenden Mikrozustande ist. E ist
groer als die experimentelle Energie-Unscharfe zu wahlen, jedoch klein verglichen mit
der Gesamtenergie E:
7.3 Die kanonische Gesamtheit
Wir fordern im Gegensatz zu Kap. 7.2 nicht mehr, da alle Systeme der Gesamtheit die
gleiche, konstante Energie E besitzen, sondern schreiben nur noch die innere Energie U
als Mittelwert vor:
U = Sp(H ) = const:
(7.17)
Dies entspricht der praktisch haug gegebenen Situation, da das betrachtete System eine schwache Wechselwirkung W mit seiner Umgebung besitzt. Dann ist die Energie des
Systems keine exakte Konstante der Bewegung; sie ist auf Grund der Wechselwirkung mit
der Umgebung Schwankungen unterworfen. Dieser Situation konnen wir im statistischen
Gleichgewicht durch die Bedingung (7.17) Rechnung tragen. Im statistischen Gleichgewicht hat die allgemeine Form
=
X
i
piji >< ij
(7.18)
mit
H ji >= Eiji > :
Unsere Aufgabe lautet nun, die Zahlen pi zu berechnen.
Dazu benutzen wir Postulat II: Wir losen das Variationsproblem
mit
unter den Nebenbedingungen
und
Dies fuhrt auf:
(,kB
X
i
(7.19)
S = 0
(7.20)
S = ,kB Sp( ln )
(7.21)
Sp() , 1 = 0
(7.22)
Sp(H ) , U = 0:
(7.23)
pi ln pi , kB ( piEi , U ) , ( pi , 1)) = 0:
X
X
i
i
61
(7.24)
Dabei sind und Lagrange-Parameter und Pi ist uber alle Zustande ji > zu erstrecken,
die zu festem Volumen V und fester Teilchenzahl N gehoren. Variation der pi ergibt analog
Fall 2):
ln pj = ,Ej , , 1;
(7.25)
kB
also
pj = const exp(,Ej ):
(7.26)
P
Die von abhangige Konstante ist so zu wahlen, da i pi = 1, also
pj = Z1 exp(,Ej );
(7.27)
k
wobei Zk die kanonische Zustandssumme ist:
Zk =
X
i
exp(,Ei):
Mit Hilfe von Zk konnen wir nun U und S ausdrucken:
X
@ ln Z
U = Z1 Ei exp(,Ei) = , @
k
k i
(7.28)
(7.29)
und
@ ln Z ):
(7.30)
S = kB (ln Zk , @
k
Auf diese Beziehungen werden wir in Kap. 9 zuruckkommen, wenn wir den Zusammenhang
von Thermodynamik und statistischer Mechanik herstellen. Dabei wird sich zeigen, da
direkt mit der Temperatur T uber T = 1= zu verknupfen ist.
Als letzte der praktisch wichtigen Gleichgewichts-Gesamtheiten betrachten wir die
7.4 Grokanonische Gesamtheit
Wir wollen ein System untersuchen, das mit seiner Umgebung nicht nur Energie (wie
im Fall 3) austauschen kann, sondern auch Teilchen. Beispiel: Gleichgewicht von Gasund Flussigkeitsphase einer bestimmten Substanz. Diesen Fall beschreiben wir, indem wir
auer der Energie nun auch die Teilchenzahl nur im statistischen Mittel festlegen, also
Sp(H ) = U
sowie
(7.31)
Sp(N^ ) = N;
(7.32)
wobei N^ der in Teil I eingefuhrte Teilchenzahl-Operator ist. In der allgemeinen Formel
fur ist jetzt uber alle Zustande zu summieren, die zu festem Volumen V gehoren, d:h.
uber alle moglichen Energien und Teilchenzahlen.
Analog dem Verfahren von 7.3 erhalten wir
pi = const exp(,Ei , Ni)
(7.33)
62
wobei mit ein weiterer Lagrange-Parameter
auftritt und Ni die Teilchenzahl im Zustand
ji > ist. Die Konstante ist wieder durch Pi pi = 1 bestimmt; mit
Zg =
X
i
exp(,Ei , Ni)
als der grokanonischen Zustandssumme wird
pi = Z1 exp(,Ei , Ni):
g
(7.34)
(7.35)
Die fundamentalen Groen U , S , N lassen sich analog 7.3 durch Zg ausdrucken:
@ ln Z
U = , @
(7.36)
g
@ ln Z
N = , @
(7.37)
g
sowie
@ ln Z , @ ln Z ) = k (ln Z + U + N ):
(7.38)
S = kB (ln Zg , @
g
g
B
g
@
7.5 Der allgemeine Fall
Im allgemeinen kann fur den Fall des statistischen Gleichgewichts von allen Erhaltungsgroen des Systems abhangen (vgl. Kap. 5.2): Energie, Impuls, Drehimpuls und Teilchenzahl; direkt verknupft mit der Teilchenzahl ist die Gesamtladung, die wir daher nicht
extra auuhren mussen. Da die uns interessierenden Systeme alle raumlich lokalisiert sind
(Beispiel: Gas im makroskopischen Behalter), entfallt der Impuls als Erhaltungsgroe des
Systems (= Gas ohne Behalter). Fur ein System in einem perfekt spharischen Behalter ist
der Drehimpuls eine Konstante der Bewegung. Da in der Praxis makroskopische Behalter
diese Forderung der spharischen Symmetrie nie hinreichend erfullen, entfallt auch der Drehimpuls als Erhaltungsgroe. Es bleiben Energie und Teilchenzahl; streng genommen sind
auch sie in der Praxis keine Erhaltungsgroen, da die Wechselwirkung zwischen System
und Umgebung nie exakt verschwindet (z:B . Wechselwirkung der Gasmolekule mit den
Wanden des Behalters). Dennoch ist die mikrokanonische Gesamtheit - der Fall des isolierten Systems - eine nutzliche Idealisierung. Realistischer sind die kanonische Gesamtheit,
wo nur die Erhaltung des Mittelwertes der Energie verlangt wird, und die grokanonische
Gesamtheit, wo schlielich Energie und Teilchenzahl nur noch im Mittel erhalten sind.
Weitere Modelle sind denkbar, in denen z:B . noch die mittlere quadratische Schwankung
von Energie und=oder Teilchenzahl fest vorgegeben ist.
7.6 Erganzungen
Im folgenden sollen einige nutzliche Formeln fur den praktischen Umgang mit der kanonischen und der makrokanonischen Gesamtheit zusammengestellt werden.
63
1. als Funktion von H und N^
Gema (7.18) und (7.27) wird
k =
da
X
i
X
i
,H ) ;
piji >< ij = Spexp(
(exp(,H ))
exp(,Ei)ji >< ij = exp(,H )
X
i
(7.39)
ji >< ij:
Entsprechend folgt fur die grokanonische Gesamtheit
^
g = exp(,H , N ^) :
Sp(exp(,H , N ))
(7.40)
(7.41)
2. Mittelwerte
In der kanonischen Gesamtheit hat ein statistischer Mittelwert die allgemeine Form
exp(,H )) ;
(7.42)
< A >k = SpSp(A(exp(
,H ))
die kanonische Zustandssumme ist
Zk = Sp(exp(,H )):
(7.43)
Bei der Spurbildung sind Zustande zu benutzen, die zu fester Teilchenzahl und festem
Volumen gehoren.
Die entsprechenden Ausdrucke fur den Fall der grokanonischen Gesamtheit lassen
sich auf (7.42) und (7.43) zuruckfuhren. Zunachst wird, da H und N^ kommutieren:
Zg = Sp(exp(,H , N^ )) = Sp(exp(,N^ ) exp(,H )) =
1
X
=0
exp(, )Zk ;
(7.44)
wobei Zk die kanonische Zustandssumme fur Teilchen ist. Die Spurbildung wird also
zunachst in den Unterraumen des Fock-Raumes (vgl. Teil I) zu fester Teilchenzahl durchgefuhrt, danach wird uber alle diese Unterraume aufsummiert. Ebenso ndet man
P1
=0 exp(, ) < A >k
< A >g = fP
(7.45)
;
=0 exp(, )Zk g
wobei < A >k der kanonische Mittelwert fur Teilchen ist. Alternativ:
^
< A >g = Sp(A exp(,^N , H )) :
(7.46)
Sp(exp(,N , H ))
3. Systeme mit makroskopisch vorgegebenem Volumen
Wahrend in der mikrokanonischen Gesamtheit E , N^ und V scharfe Werte haben, sind
in der kanonischen Gesamtheit nur noch N^ und V , in der grokanonischen nur V scharf.
64
Es liegt formal nahe, auch noch den Fall zu untersuchen, in dem auch das Volumen V
nur als Mittelwert vorgegeben ist. Wir beschranken uns der Einfachheit halber auf eine
Dimension: das Volumen werde festgelegt durch den Operator x^ der Koordinate eines
beweglichen Stempels in einem Zylinder, und der Mittelwert dieser Groe sei X . Nach
dem in 7.3 und 7.4 vorgefuhrten Verfahren erhalt man fur den statistischen Operator
^
(7.47)
= exp(,N ^, H , x^) :
Sp(exp(,N , H , x^))
Der zusatzliche Parameter wird sich im wesentlichen mit dem Druck des betrachteten
Systems verknupfen lassen. Fur S folgt analog (7.38):
S = kB (ln Z + N + U + X )
(7.48)
mit Z als der zu (7.47) gehorenden Zustandssumme. Gleichung (7.47) und (7.48) werden
sich als nutzlich erweisen, wenn wir den Zusammenhang von statistischer Mechanik und
Thermodynamik herstellen, da mit (7.47) und (7.48) auch der Fall auerer Arbeit erfat
werden kann.
65
Kapitel 8
Unabhangige identische Teilchen
8.1 Vorbemerkungen
Als ein Anwendungsbeispiel fur die Ergebnisse von Kap. 7 wollen wir ein System unabhangiger identischer Teilchen betrachten, charakterisiert durch seinen Hamilton-Operator
H=
N
X
=1
h( ):
(8.1)
Dabei haben alle Operatoren h( ) die gleiche Form und setzen sich aus kinetischer Energie
t und potentieller Energie u( ) zusammen,
h = t + u:
(8.2)
Die Eigenzustande zu H kann man sofort angeben, am bequemsten in der Teilchenzahldarstellung:
H jn1n2 :::nj :: >= E jn1 n2:::nj :: >
(8.3)
mit
X
E = ini ;
(8.4)
i
wenn i die Einteilchen-Energien (= Eigenwerte zu h) sind und ni angibt, wieviel Teilchen
sich im Einteilchen-Zustand i benden. Fur Bosonen sind fur ni die Werte 0, 1, 2,...
moglich, fur Fermionen nur 0 oder 1.
Wir wollen nun die wichtigsten statistischen Groen eines solchen Systems unabhangiger
Teilchen fur den Fall der grokanonischen Gesamtheit berechnen. Dieser Fall kommt der
Realitat am nachsten und ist uberdies rechentechnisch am einfachsten zu behandeln. Fur
groe Teilchenzahl N werden wir zeigen (Kap. 10), da man fur die mikrokanonische und
die kanonische Gesamtheit die gleichen Ergebnisse erhalt.
8.2 Mittlere Besetzungszahlen der Einteilchen-Zustande
Fur den Fall unabhangiger Teilchen erwarten wir, da sich statistische Mittelwerte des
Vielteilchensystems additiv aus Beitragen der Einteilchenzustande aufbauen lassen. Wir
66
beginnen daher mit der Berechnung der mittleren Besetzungszahlen der Einteilchenzustande
^
< ni >= Sp(^ni exp[,H , ^N ]) :
(8.5)
Sp(exp[,H , N ])
Die Auswertung von (8.5) fuhren wir in der Basis der Eigenzustande (8.3) von H durch,
in der n^i , N^ und H simultan diagonal sind. In dieser Basis wird mit (7.44)
Zg =
1
exp(, )f
X
=0
mit Pj nj = und (7.45)
< ni >= Z1
exp(,
X
1
nj
exp(, )f
X
g =0
X
nj ni
X
j
exp(,
j nj )g
X
j
j nj )g:
(8.6)
(8.7)
Kombination von (8.6) und (8.7) ergibt
(8.8)
< ni >= , ,1 @@ ln Zg ;
i
es genugt also die Berechnung von Zg als Funktion von i . Dazu schreiben wir (8.6) um:
Zg =
[(exp(,1 , ))n1 (exp(,j , ))nj ]
(8.9)
XXX
X
n1 n2 n3
nj
Wahrend in (8.6) zunachst uber die Beitrage aller -Teilchenzustande und anschlieend
uber alle Werte = 0, 1, 2,... summiert wird, werden in (8.9) die Beitrage aller Einteilchenzustande entsprechend ihrer Besetzungszahl aufsummiert. Gleichung (8.9) lat sich
noch auf Produktform umschreiben:
Y X
Zg = [ (exp(,i , ))ni ]
(8.10)
i ni
und kann nun fur Bosonen und Fermionen separat ausgewertet werden. Fur Fermionen
ist ni = 0, 1, also:
Y
Zg = f1 + exp(,i , )g:
(8.11)
i
Fur Bosonen durchlauft ni alle Werte ni = 0, 1, 2,... 1 . Damit Zg konvergiert, mussen
(bei positiv zu zahlenden i) und positiv sein, soda wir die geometrische Reihe in
(8.10) aufsummieren konnen:
Y
Zg = (1 , exp(,i , )),1:
(8.12)
i
Aus (8.11) bzw. (8.12) folgt uber (8.8)
< ni >= exp(+1+ ) + 1 fur Fermionen
i
(8.13)
< ni >= exp(+1+ ) , 1 fur Bosonen:
i
Dies sind die bekannten Bose- und Fermi-Verteilungen fur unabhangige Teilchen.
67
8.3 Mittelwerte
Fur Mittelwerte wie innere Energie U oder mittlere Teilchenzahl N des Gesamtsystems
erwartet man Ausdrucke der Form
X
U = < ni > i ;
(8.14)
i
N=
X
i
< ni > :
(8.15)
Dies ergibt sich formal aus (7.36) und (7.37) bei Benutzung von (8.11) fur Fermionen und
(8.12) fur Bosonen.
Die Gleichungen (8.14) und (8.15) legen die Lagrange-Parameter und fest: U und
N sind makroskopisch vorgegebene Groen, die Einteilchenenergien i durch die Quantentheorie (d:h. durch das Einteilchen-Potential u( )). Leider sind die Gleichungen (8.14)
und (8.15) zu kompliziert, um sie nach und auosen zu konnen.
Die Entropie lat sich ebenfalls additiv aus den Beitragen der Einteilchenzustande aufbauen, wie (7.38) direkt zeigt: auer U und N erscheint nur noch ln Zg in (7.38), und es
ist
X
ln Zg = ln(1 + exp(,i , ))
(8.16)
fur Fermionen und
i
ln Zg = ,
fur Bosonen.
X
i
ln(1 , exp(,i , ))
(8.17)
8.4 Der klassische Grenzfall
In der klassischen Physik gibt es keinen Spin. Eine klassische Naherung sollte daher so
aussehen, da der Unterschied zwischen Fermionen und Bosonen verschwindet. Betrachten
wir als eine typische Groe die mittleren Besetzungszahlen < ni >; so ergibt sich der
klassische Grenzfall, wenn
exp() 1:
(8.18)
Dann folgt aus (8.13) fur Bosonen und Fermionen
< ni >= exp(,) exp(,i ):
(8.19)
Dieses Ergebnis ist plausibel: das Pauli-Prinzip (also die Frage nach der Symmetrie der
Wellenfunktionen) wird fur Probleme der Statistik (man denke an die Zahl der Realisierungsmoglichkeiten eines bestimmten Makrozustandes) unbedeutend, wenn die Zahl der
Teilchen sehr viel kleiner ist als die Zahl der zur Verfugung stehenden Einteilchenzustande,
d:h. wenn < ni > klein ist.
Fur die durch (8.19) gegebene mittlere Besetzungszahl (Boltzmann-Statistik) kann bestimmt werden durch:
X
X
(8.20)
N = < ni >= exp(,) exp(,i);
i
i
68
also
1
exp() = N P exp(
,i) :
i
Es folgt
(8.21)
,i) :
< ni >= N exp(
(8.22)
i exp(,i )
Wir konnen die Bedingung (8.18) physikalisch interpretieren, indem wir zeigen, da fur
freie Teilchen (u( ) = 0) die Summe
P
X
i
exp(,i) V
(8.23)
wird mit V als dem vorgegebenen Volumen. Fur freie Teilchen sind die Einteilchenzustande
ebene Wellen mit Impuls p = h k und Energie = h 2 k2=(2m). Es bedeutet also, da wegen
des Spins s jede Energie noch (2s + 1)-fach entartet ist:
X
i
= (2s + 1) ;
X
k
(8.24)
dabei lauft k uber die im Normierungsvolumen V moglichen Werte. Wenn V gro ist, so
liegen die k-Werte sehr dicht und wir konnen
Z
X
V
! (2)3 d3k
(8.25)
k
ersetzen. Da in (8.23) die Energie = p2=(2m) auftritt, formen wir um
Z
Z
Z 1
1
4
3
3
d k = 3 d p = 3 p2dp
h
h 0
und erhalten schlielich (h = 2h ) :
X
i
Z 1
4
V
dp p2 exp(,p2=(2m))(2s + 1) = V (2s 3+ 1)
exp(,i) = h3
0
mit der Abkurzung
q
= h =(2m):
(8.26)
(8.27)
(8.28)
Die Groe nennt man auch thermische De-Broglie-Wellenlange. Damit lautet nun
(8.18) wie folgt:
V=N 1 : geringe Dichte!
(8.29)
Auer fur den Fall geringer Dichte erreicht man den klassischen Grenzfall (8.19) auch,
wenn klein ist. Dann wird namlich klein und somit gema (8.27) und (8.21) exp()
gro. Wenn wir aus Kap. 9 vorwegnehmen, da uber = 1=(kB T ) mit der Temperatur T
des Systems zusammenhangt, so wird der klassische Grenzfall auch fur hohe Temperaturen
erreicht.
Ergebnis: Fur niedrige Dichte und/oder hohe Temperatur gehen Bose-Statistik und
Fermi-Statistik, Gl. (8.13), in die klassische Boltzmann-Statistik uber.
69
Interessant ist noch die innere Energie fur freie klassische Teilchen. Es ist
P
X
exp(,i )
U = i < ni >= N Pi iexp(
,i)
i
i
(8.30)
X
= ,N @ ln( exp(,i ))
@
i
@ ln(V (2s + 1)=3) = 3N @ = 3 N = 3 N k T;
= ,N @
@ 2 2 B
so da im Mittel auf jedes Teilchen die Energie 3=2 kB T entfallt (Gleichverteilungssatz).
Die detaillierte Diskussion von Fermi- und Bose-Statistik werden wir im Zusammenhang
mit konkreten Beispielen (Leitungselektronen in Metallen, Gitterschwingungen Phononen, Photonen-Gas) in Teil III durchfuhren.
Warnung: Der Boltzmann-Faktor exp(,i) ist nicht zu verwechseln mit den relativen
Wahrscheinlichkeiten pj = exp(,Ej ) im statistischen Operator der kanonischen Gesamtheit! Denn: 1. ist i eine Einteilchenenergie, Ej die Energie eines Vielteilchenzustandes; 2.
gilt der obige Ausdruck fur pj generell fur eine kanonische Gesamtheit unabhangig davon,
ob unabhangige oder wechselwirkende Teilchen im System vorliegen und 3. gilt die in
Kap. 7.3 hergeleitete Form des statistischen Operators fur Fermionen wie Bosonen oder
klassische Teilchen!
70
Kapitel 9
Statistische Mechanik und
Thermodynamik
9.1 Temperatur: Warmeaustausch
Wir wollen im folgenden zeigen, da der Lagrange-Parameter mit der phanomenologischen Temperatur T uber die Relation
= k 1T
(9.1)
B
verknupft ist, wo kB die Boltzmann-Konstante ist.
Zunachst zeigen wir, da fur zwei Systeme, zwischen denen Energieaustausch moglich ist
(thermischer Kontakt), im statistischen Gleichgewicht
1 = 2
(9.2)
sein mu. Die beiden separaten Systeme 1 und 2 seien charakterisiert durch ihre Hamiltonoperatoren H1 und H2. Die vorgegebenen makroskopischen Daten seien die Teilchenzahlen N1, N2 und die Volumina V1, V2 sowie die Mittelwerte der Energie U1 = Sp(1 H1),
U2 = Sp(2H2), denen die Lagrange-Parameter 1 und 2 entsprechen (kanonische Gesamtheiten). Bringt man nun die beiden Systeme in thermischen Kontakt, so wird das
so entstehende Gesamtsystem im allgemeinen noch nicht im Gleichgewicht sein. Durch
Energieaustausch vermoge einer Wechselwirkung W zwischen den Systemen 1 und 2 wird
sich nach genugend langer Zeit ein Gleichgewicht einstellen, bei dem die Entropie S des
Gesamtsystems maximal ist. Wie wollen annehmen, da die Wechselwirkung W zwischen
den ursprunglichen Systemen so schwach ist, da sie in der Energiebilanz vernachlassigt
werden kann, obwohl sie fur die Einstellung des Gleichgewichts entscheidend ist. Unter
der Voraussetzung (s. Skizze), da N1, V1, U1 und N2 , V2, U2 bekannt sind, kennen wir
nach Einstellung des Gleichgewichts die Teilchenzahl
N = N1 + N2
(9.3)
und das Volumen
V = V1 + V2
(9.4)
71
Zwei Systeme H1 und H2 im Warmekontakt.
scharf sowie den Mittelwert der Energie des Gesamtsystems:
< H >=< H1 + H2 + W >< H1 + H2 >= U ;
(9.5)
die einzelnen Mittelwerte < H1 > und < H2 > kennen wir nicht, da zwischen den Systemen ja ein Energieaustausch stattgefunden hat. Die zu (9.3), (9.4) und (9.5) gehorende
Gesamtheit im Gleichgewicht wird durch den statistischen Operator
f, (H1 + H2)g
= Spexp
(9.6)
(expf, (H1 + H2)g)
beschrieben. Dabei ist der Lagrange-Parameter durch die Bedingung
Sp(H ) = U
(9.7)
expf, (H1 + H2 )g = exp(,H1) exp(,H2 );
(9.8)
festgelegt. Schreibt man
72
so kann man die Gleichgewichtsbedingung fur das Gesamtsystem auch formulieren als
1 = 2 = :
(9.9)
Ausgehend von den separaten Systemen mit 1 6= 2 ndet so lange Energieaustausch
statt, bis 1 = 2 = geworden ist. Genau die gleiche Eigenschaft kommt der phanomenologisch eingefuhrten Temperatur zu: Bringt man zwei Systeme mit T1 6= T2 in thermischen
Kontakt, so ndet Warmeaustausch statt, bis T1 = T2 = T geworden ist.
Aus den obigen U berlegungen folgt direkt (die Aussage wird oft als O. Hauptsatz der
Thermodynamik bezeichnet): Wenn zwei Systeme 1, 2 mit einem dritten System 3 im
thermischen Gleichgewicht sind,
1 = 3 ; 2 = 3 ;
(9.10)
so sind 1 und 2 auch untereinander im thermischen Gleichgewicht:
1 = 2 :
(9.11)
Darauf beruht die Moglichkeit der Temperaturmessung: Mit Hilfe eines Thermometers
(System 3) kann man die Temperaturen zweier Korper (Systeme 1 und 2) vergleichen.
Als Thermometer kann jedes makroskopische System dienen, welches die folgenden Voraussetzungen erfullt:
i) Bringt man das Thermometer mit dem zu untersuchenden System in thermischen Kontakt, so mu sich ein Parameter des Thermometers (z:B seine Lange oder sein elektrischer
Widerstand o.a.) monoton andern (auf Grund des zu erwartenden Energieaustausches),
bis thermisches Gleichgewicht erreicht ist.
ii) Das Thermometer mu viel kleiner sein (d:h. weniger Freiheitsgrade besitzen) als das
zu untersuchende System, damit der Energieaustausch und damit die Storung an dem zu
untersuchenden System moglichst gering ist.
Selbstverstandlich ist bei jeder Temperaturmessung so lange zu warten, bis sich thermisches Gleichgewicht zwischen Thermometer und dem zu untersuchenden System eingestellt hat.
Die obigen U berlegungen zeigen, da ein Zusammenhang zwischen der Temperatur T und
dem Lagrange-Parameter besteht,
= (T ):
(9.12)
U ber den Zusammenhang (9.12) konnen wir die folgende allgemeine Aussage beweisen: mu mit T abnehmen. Phanomenologisch wissen wir, da hohere Temperatur hohere
Energie bedeutet. Andererseits gilt im Rahmen der statistischen Mechanik (vgl. Kap. 10):
(H )2 =< H 2 > , < H >2= , @U
(9.13)
@ 0:
Um den genauen funktionalen Zusammenhang von und T zu nden, betrachten wir nun
ein ideales Gas. Dafur hatten wir in Kap. 8, Gl. (8.30), gefunden:
U = 23 N ,1;
(9.14)
73
wahrend die phanomenologische Thermodynamik liefert
(9.15)
U = 32 N kB T:
Wir identizieren daher
= k 1T :
(9.16)
B
Dabei haben wir (stillschweigend) davon Gebrauch gemacht, da die thermodynamisch
denierte innere Energie U mit Sp(H ) zu identizieren ist. Diese Identikation folgt
zwangslaug, wenn man die Beschreibung eines realen makroskopischen Systems durch
eine statististische Gesamtheit akzeptiert! In 9.5 werden wir anhand der idealen GasGleichung PV = NkB T die Relation (9.16) bestatigen.
Anmerkung: Die obigen U berlegungen uber die Temperatur eines Systems lassen sich
auch im Rahmen der mikrokanonischen Gesamtheit durchfuhren, wo zu Beginn die Systeme 1 und 2 als isoliert betrachtet werden, ebenso nach Einstellung des Gleichgewichts das
Gesamtsystem. Wenn W im Rahmen der Energiebilanz vernachlassigbar ist (wie oben
vorausgesetzt), so setzen sich Energie E (scharfer Wert!) und Entropie S des Gesamtsystems additiv aus den entsprechenden Groen der Einzelsysteme zusammen (Volumen
und Teilchenzahl sind ja fest!) Der Gleichgewichtszustand ist charakterisiert durch
@S )E + ( @S )E = 0
S = ( @E
(9.17)
1
@E2 2
1
unter der Nebenbedingung
E = 0 ! E1 = ,E2 :
(9.18)
Kombination von (9.17) mit (9.18) ergibt die Gleichgewichtsbedingung
@S = @S ;
(9.19)
@E1 @E2
welche zu Gl. (9.2) aquivalent ist in der Form
@S = @S = :
(9.20)
@U1 @U2
Die durch @S=@E denierte Temperatur der mikrokanonischen Gesamtheit ist nicht
identisch mit der durch @S=@U denierten Temperatur der kanonischen Gesamtheit;
der Unterschied verschwindet jedoch mit wachsender Teilchenzahl (vgl. Kap. 10).
9.2 Chemisches Potential: Teilchenaustausch
Wir untersuchen als nachstes zwei Systeme, die sowohl Energie als auch Teilchen austauschen konnen. Die Behandlung geschieht analog zum Warmeaustausch. Die beiden
separaten Systeme werden als grokanonische Gesamtheit beschrieben:
^
(9.21)
i = expf,iHi , iNi^g
Sp(expf,i Hi , iNig)
74
fur i = 1, 2, wobei im allgemeinen
1 6= 2; 1 6= 2
(9.22)
sein wird. Bringt man die Systeme in Kontakt, so da sie Energie und Teilchen austauschen
konnen, so stellt sich nach genugend langer Zeit ein Gleichgewicht fur das Gesamtsystem
ein. Der statistische Operator des Gesamtsystems, fur das
U = Sp(H )
(9.23)
und
N = Sp(N^ )
(9.24)
H = H1 + H2 (+W ); N^ = N^1 + N^2;
(9.25)
bekannt sind, hat die Form:
^ ^
= expf, [H1 + H2 ] , [N1^ + N2^]g :
(9.26)
Sp(expf, [H1 + H2] , [N1 + N2 ]g)
Da der exp- Operator in (9.26) sich aufspalten lat in
expf,H1 , N^1 g expf,H2 , N^2g;
(9.27)
lauten die Gleichgewichtsbedingungen:
1 = 2 ; 1 = 2 :
(9.28)
U blicherweise fuhrt man statt die Groe
= , (9.29)
ein, so da (9.28) ubergeht in
1 = 2; 1 = 2:
(9.30)
Da der Gleichgewichtsparameter bei chemischen Reaktionen (Beispiel: Dissoziation von
atomarem Wassersto: H $ p + e) eine wichtige Rolle spielt, nennt man ihn allgemein
chemisches Potential.
Die Gleichgewichtsbedingungen lassen sich auch fur den Fall formulieren, da sowohl die
separaten Systeme als auch das Gesamtsystem isolierte Systeme sind (mikrokanonische
Gesamtheit). Der Gleichgewichtszustand des Gesamtsystems ist dann, da V = V1 + V2
fest ist, charakterisiert durch
@S )E + ( @S )E + ( @S )N + ( @S )N = 0
S = ( @E
(9.31)
1
@E2 2 @N1 1 @N2 2
1
bei
N = 0 ! N1 = ,N2
(9.32)
und
E = 0 ! E1 = ,E2 :
(9.33)
75
Dies ergibt die Gleichgewichtsbedingungen
@S = @S ; @S = @S ;
(9.34)
@E1 @E2 @N1 @N2
welche - in U bereinstimmung mit (9.20) - fur den Fall der grokanonischen Gesamtheit
lauten:
@S = @S ; @S = @S :
(9.35)
@U1 @U2 @ N1 @ N2
Man beachte, da analog 9.1 nur fur groe Teilchenzahlen @S=@N = @S=@ N wird.
9.3 Druck: Volumenaustausch, auere Arbeit
Im allgemeinen Fall, wo fur die Einzelsysteme wie fur das Gesamtsystem nur die Mittelwerte von Energie, Teilchenzahl und Volumen festgelegt sind, hat der statistische Operator
des Gesamtsystems nach Einstellung des Gleichgewichts die Form (vgl. Gl. (7.47)):
^
(9.36)
= expf,N ^, H , x^g :
Sp(expf,N , H , x^g)
Dies entspricht der Situation, wo die beiden Systeme 1 und 2 durch einen in x-Richtung
(frei) beweglichen Stempel getrennt sind, welcher zugleich fur Energie und Teilchen durchlassig
ist.
Im Gleichgewicht mu entsprechend den U berlegungen zu 1) und 2) gelten:
und
1 = 2 (therm: Gleichgewicht)
(9.37)
1 = 2 (chemisches Gleichgewicht)
(9.38)
1 = 2 (mechanisches Gleichgewicht):
(9.39)
76
Mit (vgl. Gl. (7.48))
S = kB (ln Z + N + U + X )
(9.40)
konnen wir (9.37), (9.38), (9.39) auch schreiben als
@S = @S ; @S = @S ; @S = @S
(9.41)
@U1 @U2 @ N1 @ N2 @X1 @X2
in Analogie zu (9.35).
Um den Parameter mit dem Druck in Verbindung zu bringen, denken wir uns System
2 durch eine auere Kraft (Gewicht im Schwerefeld, vorgespannte Feder) ersetzt.
Beispiel fur ein System unter dem Einu einer aueren Kraft f = ,Mg.
Den statistischen Operator fur das Gleichgewicht erhalt man dann, indem man zum
Hamilton-Operator H des Systems die potentielle Energie ,f x^ des Stempels hinzufugt,
also ansetzt:
= (H , f x^; N^ ):
(9.42)
Der Vergleich mit (7.47) fuhrt dann auf
= , f;
(9.43)
wobei f die konstante auere Kraft ist. Wir konnen daher
@S = T @S = =: P
T @V
(9.44)
F @X F
als den Druck P des Systems auf den Stempel auassen; F sei die Flache des Stempels.
U bertragen wir dieses Ergebnis auf unser ursprungliches Beispiel, so sehen wir, da die
Gleichgewichtsbedingung @S=@V1 = @S=@V2 gerade P1 = P2 bedeutet. V bzw. Vi bedeuten
die Mittelwerte der Volumina der betreenden Systeme.
Ergebnis: Die formalen Lagrange-Parameter , und haben wir verknupft mit Tem-
peratur T , chemischem Potential und Druck P . Also: Zu vorgegebener innerer Energie
U gehort ein bestimmter Wert von T , zu vorgegebener mittlerer Teilchenzahl N ein bestimmter Wert von und zu vorgegebenem Mittelwert V des Volumens ein bestimmter
Druck P:
77
9.4 Einfache Beispiele
In diesem Abschnitt behandeln wir einige einfache Beispiele fur die oben hergeleiteten
Gleichgewichtsbedingungen (9.41)
T1 = T2 ; P1 = P2; 1 = 2 :
Dabei wird die Bedingung 1 = 2 im Vordergrund stehen, welche das chemische Gleichgewicht (Gleichgewicht gegenuber Teilchenaustausch) beschreibt. Die Systeme 1 und 2,
die miteinander im Gleichgewicht sein sollen, wollen wir als homogen annehmen (N =V =
const). Dann sind Teilchenzahl und Volumen keine unabhangigen Variablen des Systems,
was zur Folge hat, da die drei Bedingungen (9.42) nicht unabhangig sind. Man kann
daher z:B . als Funktion von P und T auassen
= (P; T );
womit in (9.41) die dritte Bedingung aus den beiden ersten folgt.
Beispiel 1: Phasengleichgewichte
Erfahrungsgema kann ein- und dieselbe Substanz, bestehend aus einer bestimmten Sorte
von Atomen oder Molekulen, in verschiedenen Modikationen (Phasen) vorkommen. Verschiedene Phasen besitzen verschiedene physikalische Eigenschaften wie Dichte, Kompressibilitat, Suszeptibilitat etc. Man unterscheidet zunachst grob feste, ussige und gasformige Phasen; feste und ussige Phasen konnen ihrerseits noch in verschiedenen Modikationen vorkommen, etwa als verschiedene Gitterstrukturen der gleichen Substanz, oder in
ferromagnetischen, supraleitenden, suprauiden Phasen.
Phasengleichgewicht liegt vor, wenn zwei oder mehrere Phasen miteinander in Kontakt
sind und die Gleichgewichtsbedingungen (9.41) erfullt sind. Es handelt sich dann insgesamt um ein inhomogenes System; jede einzelne Phase kann jedoch fur sich genommen
als homogen angesehen werden.
Fur ein Zweiphasensystem eines Stoes lautet Gleichung (9.41)
1(P; T ) = 2 (P; T );
(9.45)
wobei P und T die beiden Phasen gemeinsamen Groen Druck und Temperatur sind.
Durch (9.45) wird in der P , T -Ebene (siehe Figur) eine Kurve P = P (T ) festgelegt,
auf der zwei Phasen koexistieren konnen. Auf den beiden Seiten einer solchen Grenzkurve
kann dagegen jeweils nur eine Phase existieren.
Beispiel fur ein P , T -Diagramm
Beim Dreiphasensystem eines Stoes lauten die Gleichgewichtsbedingungen fur Teilchenaustausch
1(P; T ) = 2(P; T ) = 3(P; T ):
(9.46)
Durch (9:46) wird im P , T Diagramm ein Punkt festgelegt (tr ), der sog. Tripelpunkt,
in dem alle drei Phasen simultan existieren konnen. Oensichtlich konnen nicht mehr als
drei Phasen eines Stoes im Gleichgewicht sein. Oberhalb eines kritischen Punktes (kr )
ist eine eindeutige Unterscheidung von Flussigkeit und Gas nicht mehr moglich.
78
Beispiel fur ein P -T -Diagramm
Verallgemeinert man die obigen U berlegungen, so erhalt man die Phasenregel von
Gibbs:
Fur n verschiedene Stoe hangen die chemischen Potentiale ai(i = Phase, a = Sto) in
jeder Phase auer von P und T noch von den (n , 1) Konzentrationen der Stoe ab.
Sind r Phasen im Gleichgewicht, so erhalt man als Gleichgewichtsbedingungen (analog
(9.46)) n (r , 1) Gleichungen. Die Variablen, von denen die ai abhangen, sind P und
T sowie (n , 1) Konzentrationen fur jede Phase; dies sind 2 + r (n , 1) Variable. Bei
Berucksichtigung der n (r , 1) Gleichgewichtsbedingungen bleiben also
f = 2+n,r
(9.47)
freie unabhangige Variable ubrig. f gibt die Zahl der Variablen an, die man ohne Zerstorung
des Gleichgewichts beliebig andern darf. Ist f = 0, also r = n +2, so sind durch die Gleichgewichtsbedingungen alle Variablen festgelegt, - man kann keine der Variablen andern,
ohne das Gleichgewicht zu zerstoren. - Die Maximalzahl der Phasen eines Systems mit n
Komponenten (Stoen), die simultan im Gleichgewicht sind, ist also n + 2:
Beispiel 2: Chemische Reaktionen
Chemische Reaktionen, die in einer Mischung von miteinander reagierenden Stoen ablaufen, fuhren schlielich dazu, da sich ein Gleichgewichtszustand einstellt, in welchem
sich die Mengen der an der Reaktion beteiligten Stoe nicht mehr andern: chemisches
Gleichgewicht. Jede chemische Reaktion lauft im allgemeinen in beiden Richtungen; vor
Erreichen des Gleichgewichts uberwiegt eine Reaktionsrichtung, im Gleichgewicht laufen
die beiden entgegengesetzten Reaktionen mit solchen Geschwindigkeiten ab, da die Gesamtmenge eines jeden an der Reaktion beteiligten Stoes sich nicht mehr andert.
Gegenstand der Thermodynamik der chemischen Reaktionen ist nur die Untersuchung des Gleichgewichts, nicht die der Prozesse, die zum Gleichgewicht fuhren.
79
Bei einer chemischen Reaktion konnen sich die Teilchenzahlen der verschiedenen Reaktionspartner nicht beliebig andern. Zum Beispiel ist bei der Reaktion
stets
oder bei
ist
H + D , HD
(9.48)
NH = ND = ,NHD ;
(9.49)
2H2 + O2 , 2 H2 O
(9.50)
NH2 = ,NH2 O = 2 NO2 :
Schreibt man eine chemische Reaktion als
i Ai = 0;
X
i
(9.51)
(9.52)
wobei Ai das chemische Symbol der i , ten Teilchenart bedeutet, so ist
Ni = iN;
(9.53)
wenn N die Zahl der elementaren Reaktionen ist. Der Gleichgewichtszustand eines abgeschlossenen Systems besitzt dann ein Maximum der Entropie S bzgl. der A nderungen
der Ni unter den Nebenbedingungen (9.53). Setzt man also
@S )N = 0
S = ( @N
(9.54)
i
i
i
in Gleichung (9.53) ein, so entsteht als Bedingung fur chemisches Gleichgewicht:
i i = 0:
(9.55)
X
X
i
Kennt man die chemischen Potentiale i der Reaktionspartner
als Funktion von Druck
P
P , Temperatur T und der Konzentrationen ci = Ni=( i Ni), so ergibt Gleichung (9.55)
eine Relation zwischen den ci, P und T (Massenwirkungsgesetz).
9.5 Einstellung des Gleichgewichts
Gemessen an der Theorie des statistischen Gleichgewichts ist die Theorie thermodynamischer Prozesse - speziell die Einstellung des Gleichgewichts - eher noch in den Anfangen.
Daher werden zu diesem Thema hier nur einige qualitative Aussagen gemacht, welche die
in 9.1 - 9.3 besprochene Verknupfung thermodynamischer Groen (, T , P ) mit Groen
der statistischen Mechanik (Lagrange-Parameter , , ) bestatigen. Fur die Behandlung
thermodynamischer Prozesse sei auf Kap. 14 verwiesen.
Wir betrachten als erstes den Fall der Einstellung thermischen Gleichgewichts. Die beiden
Systeme 1, 2 seien anfangs gekennzeichnet durch 1 > 2. Bringt man das System in
80
thermischen Kontakt, so wird die Entropie von 1+2 anwachsen, da wir die Festlegung der
inneren Energien U1 und U2 durch nur noch eine Bedingung fur die gesamte innere Energie
U ersetzen, also Information verlieren. Nach Herstellung des thermischen Kontakts wird
also S zunehmen, so da bei quasi-statischer Prozefuhrung (s:u:) aus
folgt:
wenn man benutzt
S > 0
(9.56)
@S1 , @S2 )U > 0;
( @U
@U 1
(9.57)
1
2
U1 = ,U2 :
Mit 1 = @S1 =@U1 , 2 = @S2 =@U2 wird
(9.58)
(1 , 2)U1 > 0
(9.59)
U1 > 0:
(9.60)
oder, da 1 > 2 vorausgesetzt war,
Gleichung (9.60) besagt, da die Energie des Systems mit der tieferen Temperatur zunimmt, bis thermisches Gleichgewicht erreicht ist.
Wir betrachten nun 2 Substanzen, welche miteinander im thermischen Gleichgewicht sind,
jedoch noch nicht im mechanischen: 1 > 2(P1 > P2 ). Das Gesamtsystem entwickelt sich
dann so, da die Entropie anwachst, bis auch mechanisches Gleichgewicht herrscht. Nachdem man die Systeme in Kontakt gebracht hat, ist also entsprechend den U berlegungen
zu Fall 1:
(P1 , P2 )V1 > 0:
(9.61)
Da P1 > P2 vorausgesetzt war, folgt:
V1 > 0;
(9.62)
also: das System mit dem hoheren Druck expandiert, bis auch mechanisches Gleichgewicht
erreicht ist.
Nach dem gleichen Verfahren beweist man, da bei der Einstellung des chemischen Gleichgewichts das System mit dem hoheren chemischen Potential Teilchen an das System
mit niedrigerem chemischen Potential abgibt.
9.6 Thermodynamische Potentiale
In der phanomenologischen Thermodynamik kann jeder Gleichgewichtszustand durch genau 1 Funktion der naturlichen Variablen des Systems vollstandig beschrieben werden.
Eine solche Funktion, aus der sich durch Dierenziation alle weiteren thermodynamischen Groen bestimmen lassen, heit thermodynamisches Potential. Die naturlichen
81
Variablen sind die unabhangig experimentell vorgegebenen Variablen des Systems; bei
Abwesenheit auerer Felder und fur Systeme identischer Teilchen gibt es je nach den
makroskopischen Bedingungen 3 solche Variablen, z:B . E , V , N fur ein isoliertes System
oder T , V , N fur ein System in thermischem Kontakt mit einem Warmereservoir. Je nach
der Wahl der naturlichen Variablen gibt es verschiedene thermodynamische Potentiale.
So ist die freie Energie F =: U , TS das thermodynamische Potential der naturlichen Variablen T , V , N , wahrend zu T , P , N die freie Enthalpie G =: U , TS + PV
thermodynamisches Potential ist.
Die Bedeutung der naturlichen Variablen wird besonders klar aus der Sicht der statistischen Mechanik: Fur jedes System einer statistischen Gesamtheit haben die naturlichen
Variablen den gleichen, festen Wert, die anderen thermodynamischen Groen sind nur als
Mittelwerte zu verstehen und Fluktuationen unterworfen. Diesen Unterschied kennt die
phanomenologische Thermodynamik nicht; statistische Mechanik und phanomenologische
Thermodynamik konnen also erst dann miteinander voll in Einklang gebracht werden,
wenn die Fluktuationen der Mittelwerte verschwindend klein werden, d:h. fur sehr groe
Teilchenzahlen (vgl. Kap. 10).
In der folgenden Tabelle (*) sind die praktisch wichtigsten thermodynamischen Potentiale und ihre naturlichen Variablen zusammengestellt.
thermodyn. Potential naturliche Variable totales Dierential
I S
E; V; N
dS = T1 dE + PT dV , T dN
II F = U , TS
T; V; N
dF = ,SdT , PdV + dN
III G = U , TS + PV T; P; N
dG = ,SdT + V dP + dN (9.63)
IV J =: E , TS , N T; V; dJ = ,SdT , PdV , Nd
V U
S; V; N
dU = TdS , PdV + dN
mit der Entropie S , der freien Energie F , der freien Enthalpie G, dem grokanonischen Potential J und der inneren Energie U .
Die totalen Dierentiale geben an, wie die thermodynamischen Potentiale sich bei quasistatischen Prozessen andern auf Grund innitesimaler A nderung der naturlichen Variablen. Quasi-statische Prozesse sind solche, die langsam verglichen mit der Einstellzeit des
Gleichgewichts verlaufen; es wird also eine Kette von nahe beieinander liegenden Gleichgewichtszustanden durchlaufen. Quasi-statische Prozesse konnen sowohl reversibel als auch
irreversibel sein. Ein einfaches Beispiel ist der Warmeaustausch zwischen 2 Systemen mit
einer endlichen Temperaturdierenz durch einen sehr schlecht warmeleitenden Kontakt.
Ein solcher Proze ist quasi-statisch, jedoch irreversibel.
Wir beginnen mit der Diskussion von Fall I, in dem E , N , V die naturlichen Variablen sind. Dies ist der Fall eines abgeschlossenen Systems, den wir mit Hilfe der
mikrokanonischen Gesamtheit beschreiben konnen. Dafur hatten wir in Kap. 7.2 gefunden:
S = kB ln Zm;
(9.64)
wo die Zahl der Realisierungsmoglichkeiten des Makrozustandes Zm eine Funktion von E ,
V , N ist,
Zm = Zm (E; V; N ):
(9.65)
82
Also wird auch
S = S (E; V; N ):
(9.66)
S ist in der Tat das gesuchte thermodynamische Potential Entropie. Dazu bilden wir das
totale Dierential
@S )dE + ( @S )dV + ( @S )dN
(9.67)
dS = ( @E
@V
@N
und berucksichtigen die Ergebnisse aus 9.1 - 9.3. Bei quasi-statischer Prozefuhrung ist
@S=@E gerade uber
@S = 1
(9.68)
@E T
mit der Temperatur T (der mikrokanonischen Gesamtheit) verknupft; entsprechend
@S = , (9.69)
@N
T
und
@S = P ;
(9.70)
@V T
wobei P der Druck und das chemische Potential (der mikrokanonischen Gesamtheit)
ist. Damit wird wie gefordert (siehe Tabelle)
TdS = dE + PdV , dN ;
(9.71)
diese Relation wird uns bei der Diskussion des 1. Hauptsatzes der Thermodynamik wieder
begegnen. Es ist allerdings zu beachten, da die oben eingefuhrten Groen T , P und nur
dann mit den in 9.1 - 9.3 diskutierten Groen ubereinstimmen, wenn die Fluktuationen
von U , N und V verschwindend klein werden (vgl. Kap. 10).
Wir wahlen nun T; V; N als naturliche Variable. Da nach Abschnitt 9.1 T = 1=(kB ) ist
und da die innere Energie U eines Systems (als Mittelwert!) festlegt, konnen wir auch
U; V; N als gegeben ansehen, ,V und N als scharfe Werte, U als Mittelwert. - Dies ist
genau die Situation, die wir mit Hilfe der kanonischen Gesamtheit beschrieben haben.
Fur die Zustandssumme Zk hatten wir gefunden (Kap. 7):
Zk = expf,Eig;
(9.72)
X
i
zu summieren ist uber alle Mikrozustande zu fester Teilchenzahl N und festem Volumen
V ; Ei sind die zugehorigen Energien des Systems. Da die Energien Ei von N und V als
Parameter abhangen, ist
Zk = Zk (; N; V ):
(9.73)
Das gesuchte thermodynamische Potential ist
F =: kB T ln Zk = U , TS;
(9.74)
vgl. (7.30), in U bereinstimmung mit der phanomenologischen Thermodynamik. Fur das
totale Dierential erhalt man
dF = dU , TdS , SdT;
(9.75)
83
oder, wenn man die Fluktuationen von U vernachlassigt und dU aus der Tabelle (*)
ubernimmt:
dF = (TdS , PdV + dN ) , TdS , SdT = ,SdT , PdV + dN:
(9.76)
Entsprechende U berlegungen konnen auf die Falle III und V angewendet werden. Die
allgemeine Gleichgewichtsbedingung S = 0 geht fur die Falle II bis V uber in die entsprechende Bedingung fur F , U , G bzw. J .
Eine Reihe nutzlicher Relationen (die Maxwell-Relationen) ergeben sich aus den Integrabilitatsbedingungen fur die totalen Dierentiale fur S , F , G, U , J und weitere (praktisch weniger wichtige) thermodynamische Potentiale.
Beispiel: Damit (9.76) totales Dierential von F = F (T; V; N ) ist, mu u:a. erfullt sein:
@S ) = ( @P ) ;
( @V
(9.77)
T;N
@T V;N
wobei die Indizes angeben, welche Groen bei Bildung der partiellen Ableitung fest zu
halten sind. Weitere Maxwell-Relationen werden in den U bungen explizit diskutiert.
9.7 Die Hauptsatze der Thermodynamik
Der 1. Hauptsatz ist nichts anderes als eine fur die Zwecke der Thermodynamik geeignete
Formulierung des allgemeinen Energiesatzes:
1. Die Energie eines isolierten Systems ist zeitlich konstant.
Diese Aussage liefert auch die statistische Mechanik, denn ein isoliertes System wird
durch die mikrokanonische Gesamtheit beschrieben, fur die alle Systeme der Gesamtheit
die gleiche, zeitlich konstante Energie haben.
2. Die innere Energie eines Systems andert sich, wenn dem System Energie
zugefuhrt (entzogen) wird.
Die A nderung U zerlegt man in der Thermodynamik in 2 Anteile: die am (vom) System von (an) der Umgebung geleistete Arbeit W und die aufgenommene (abgegebene)
Warme Q;
U = Q + W:
(9.78)
Diese Aufteilung ist nicht durch Anfangs- und Endzustand des Systems bestimmt, sondern
hangt vom Charakter des Prozesses ab; die Groen W und Q sind also keine thermodynamischen Potentiale. Zur begriichen Unterscheidung von W und Q betrachten wir die
(aueren) Parameter des Systems wie Volumen, auere Felder, raumliche Position des
Systems etc.: W ruhrt her von der A nderung der aueren Parameter, z:B . dem Volumen, wahrend Q 6= 0 auch dann sein kann, wenn auere Parameter sich nicht andern.
Beispiel: Man nehme eine Flasche Sekt aus dem Kuhlschrank und stelle sie (auf gleicher
Hohe) auf einen Tisch. Dann ist W = 0, da keine Arbeit geleistet wird. Trotzdem wird
von der Umgebung Energie auf die Flasche Sekt ubertragen, namlich in Form von Warme:
84
U = Q 6= 0; dabei andert der Sekt seinen Zustand, - er wird warmer und schmeckt
schlechter. Um den 1. Hauptsatz in Form der Energiebilanz (9.78) aus der statistischen Mechanik herzuleiten, zerlegen wir den Proze der Energieanderung in lauter quasi-statische Schritte.
Fur jeden solchen Schritt gilt gema der Tabelle
dU = TdS , PdV + dN;
(9.79)
oder (wie in (9.78) stillschweigend angenommen) bei fester Teilchenzahl
dU = TdS , PdV:
(9.80)
Der 2. Term ist oensichtlich mit der geleisteten Arbeit zu identizieren
W = ,PdV:
(9.81)
Damit bleibt
Q = TdS:
(9.82)
(Bemerkung: Wir schreiben W und Q, um anzudeuten, da W und Q keine thermodynamischen Potentiale sind.)
Gleichung (9.82) ist in Einklang mit der im Rahmen des 2. Hauptsatzes ausgesprochenen
Verknupfung von Entropie und Warme, wenn wir die fehlende Information S mit der
Entropie identizieren. Bevor wir diesen Gedanken fortfuhren, wollen wir noch einmal
kurz auf die Aufspaltung von dU in die beiden Anteile Warme und Arbeit zuruckkommen.
Ausgehend von der allgemeinen Formel fur den Mittelwert der inneren Energie
U=
bilden wir
dU =
X
i
X
i
piEi
Eidpi +
X
i
(9.83)
pidEi:
(9.84)
Da Warme-Transfer bei festen aueren Parametern erfolgt, und da bei festen aueren
Parametern (z:B . Volumen) die Energieeigenwerte des Systems festliegen, stellt der 1.
Term in (9.84) den Warme-Transfer dar,
Q =
X
i
Eidpi;
(9.85)
herruhrend von einer A nderung der die Gesamtheit beschreibenden Wahrscheinlichkeiten
pi. Damit folgt fur die geleistete Arbeit
W =
X
i
pidEi;
(9.86)
sie ruhrt her von einer durch A nderung auerer Parameter bedingten A nderung der Energieniveaus des Systems.
85
Der 2. Hauptsatz der Thermodynamik besagt, da einem makroskopischen System
im Gleichgewicht eine Groe Entropie zugeordnet werden kann, welche folgende Eigenschaften besitzt:
1. Bei quasi-statischer Prozefuhrung ist die vom System aufgenommene Warme Q
mit einer Entropieanderung dS verknupft durch
dS = Q
(9.87)
T;
wobei T die Temperatur des Systems im Gleichgewicht ist.
2. Die Entropie eines isolierten Systems kann niemals abnehmen (S 0):
Die von uns eingefuhrte fehlende Information S besitzt nach Gleichung (9.82) und (6.36)
genau die oben geforderten Eigenschaften und kann daher endgultig mit der Entropie
identiziert werden. Prozesse, fur die S (0) = S (t) gilt, nennt man reversibel, solche mit
S (0) < S (t) irreversibel. Irreversible Prozesse sind also solche, die von allein nur in einer
Richtung laufen; reversible Prozesse sind Idealisierungen, die fur den Aufbau der Thermodynamik unentbehrlich sind (Beispiel: Carnot'scher Kreisproze). Jeder reale Proze
enthalt irreversible Anteile und lauft von selbst solange, bis die Entropie ein Maximum
erreicht: statistisches Gleichgewicht.
Anmerkungen:
) U bertragt man die obigen Aussagen naiv auf das gesamte Universum, so mute dessen
Entropie laufend ansteigen, bis totales Gleichgewicht erreicht ist (Warmetod). Diese
U berlegung ist jedoch nicht schlussig, da wir die statistische Mechanik im Rahmen einer
nichtrelativistischen Theorie aufgebaut haben, welche sicher nicht auf das Universum als
Ganzes anwendbar ist.
) Man beachte, da (9.71) nur fur quasi-statische Prozesse gilt. Ist diese Bedingung nicht
erfullt, so gilt stattdessen die Ungleichung
TdS > dE + PdV , dN:
(9.88)
3. Die Entropie ist eine extensive Groe.
Diese Eigenschaft der Additivitat gilt auch fur die fehlende Information S : Betrachtet
man 2 unabhangige Systeme 1, 2 mit den statistischen Operatoren 1 , 2 als ein neues,
kombiniertes System 1 + 2, so ist dessen statistischer Operator gegeben durch
1+2 = 1 2 = 2 1 ;
(9.89)
dazu beachte man, da die Mikrozustande des kombinierten Systems direkte Produkte
der Mikrozustande der einzelnen Systeme sind. Setzt man 1 , 2 als normiert voraus, so
folgt:
S1+2 = ,kB Sp(12 fln 1 + ln 2g) = S1 + S2
(9.90)
wie oben behauptet.
Anmerkung: In der Thermodynamik unterscheidet man extensive Groen (wie Volumen V , innere Energie U , Entropie S ) von intensiven Groen (wie Temperatur T , Druck
86
P , Dichte N =V ). Intensive Groen andern sich nicht, wenn man ein homogenes System
in kleinere (aber immer noch groe) Systeme unterteilt, extensive Groen nehmen ab im
Verhaltnis der Teilchenzahlen.
Beispiel: Ein homogenes System mit Teilchenzahl N , innerer Energie U und Druck P
werde halbiert: N1 = N2 = 1=2N ; dann ist P1 = P2 = P , aber U1 = U2 = 1=2U:
Der 3. Hauptsatz macht eine weitere Aussage uber die Entropie S : Fur jedes reine
System, welches nur 1 Sorte Teilchen enthalt, gilt
S (T = 0; ::::) = 0
(9.91)
unabhangig von den Werten anderer Groen (z:B . Druck oder aueres Magnetfeld), von
denen S noch abhangt. Fur Systeme mit mehreren Teilchensorten bleibt fur T ! 0 eine
von null verschiedene Mischungsentropie.
Die obige Aussage lat sich wie folgt aus der statistischen Mechanik ableiten: Der Hamiltonoperator besitzt ein diskretes und nach unten begrenztes Spektrum,
E0 < E1 < E2 < :
(9.92)
E1 , E0 kB T;
(9.93)
pi = g1
(9.94)
Wenn T genugend klein ist, d:h:
so folgt aus (7.27)
0
fur die zu E0 gehorenden Zustande,
pi = 0 sonst;
wobei g0 der Entartungsgrad des Grundzustandes ist. Also wird
lim S = kB ln g0;
T !0
(9.95)
so da fur Systeme mit nicht-entartetem Grundzustand, g0 = 1, gerade
lim S = 0
T !0
(9.96)
wird. Konkrete Beispiele sind freie Fermionen und freie Bosonen, wofur (9.96) direkt
bewiesen werden kann (vgl. Kap. 11 und Kap. 12). Dagegen ist fur ein klassisches ideales
Gas Gleichung (9.96) nicht erfullt (siehe Abschnitt 9) - die klassische Theorie ist bei
niedrigen Temperaturen nicht mehr anwendbar (vgl. Kap. 8.4) - .
Der 3. Hauptsatz ist in der oben gegebenen Formulierung experimentell nicht uberprufbar,
da nur Entropie-Dierenzen mebar sind. Er besitzt aber eine Reihe direkt uberprufbarer
Konsequenzen, von denen einige im folgenden besprochen werden.
87
9.8 Spezische Warme
Warmezufuhr erhoht die Temperatur eines Systems entsprechend seiner Warmekapazitat.
Letztere hangt sowohl von der Natur des Systems als auch der Art der Erwarmung ab.
Bei fester Teilchenzahl und ohne auere Felder mussen wir unterscheiden: Erwarmung bei
konstantem Volumen mit der Warmakapazitat
CV =: ( @U
(9.97)
@T )V
und Erwarmung bei konstantem Druck, wo man als Warmekapazitat CP deniert
+ PV ] ) ;
CP =: ( @ [U @T
(9.98)
P
die Groe U + PV heit Enthalpie.
Die Def. (9.97) wird sofort plausibel, wenn man das totale Dierential von U schreibt
als
dU = Q , PdV + dN
(9.99)
und auf den Fall konstanter Teilchenzahl (dN = 0) und konstantem Volumen (dV = 0)
spezialisiert. Um (9.98) zu begrunden, betrachtet man das totale Dierential von U + PV;
d[U + PV ] = Q + V dP + dN;
(9.100)
und spezialisiert auf konstanten Druck (dP = 0) und konstante Teilchenzahl (dN = 0):
Wir wollen nun zeigen, da die spezische Warme (=Warmekapazitat pro Masseneinheit) in beiden Fallen als Folge des 3. Hauptsatzes bei T = 0 verschwinden mu. Wir
fuhren den Beweis fur CV durch, fur CP verlauft er analog. Fur dV = dN = 0 lat sich
(9.99) mit (9.87) schreiben als
(9.101)
dS = CTV dT
oder in Integralform
Z T
(9.102)
S (T ) = CTV0 dT 0;
0
da ja S (T = 0) = 0. Damit S (T ) endlich bleibt, mu CV fur T 0 = 0 verschwinden, um die
von 1=T 0 herruhrende Singularitat zu beseitigen.
Damit konnen wir sofort beweisen, da das Modell des klassischen idealen Gases am
absoluten Nullpunkt falsch ist. Wir hatten in Kap. 8.4 fur den Mittelwert der inneren
Energie gefunden:
U = 23 N kB T;
(9.103)
so da folgt:
(9.104)
CV = 23 kB N 6= 0
unabhangig von T , im Widerspruch zum 3. Hauptsatz. In Teil III werden wir zeigen, da
das ideale Fermi-Gas und das ideale Bose-Gas mit dem 3. Hauptsatz in Einklang sind.
88
9.9 Thermischer Ausdehnungskoezient
Aus Fall III der Tabelle (*) folgt die Maxwell-Relation (fur dN = 0)
(9.105)
( @S )T = ,( @V )P :
@P
@T
Da nun S (T; P ) ! 0 fur T ! 0 fur alle Werte von P (oder sonstiger anderer Parameter,
von denen S abhangen kann), folgt
@V ) = 0;
lim
(
(9.106)
T !0 @T P
d:h. der thermische Ausdehnungskoezient bei konstantem Druck verschwindet am absoluten Nullpunkt. Damit lat sich am Beispiel einer adiabatischen Druckanderung die
Unerreichbarkeit des absoluten Nullpunkts demonstrieren.
Zunachst zeigen wir, da fur eine adiabatische (dS = 0) Druckanderung gilt
dT = ( @V
)P T dP:
(9.107)
@T CP
Beweis: Wir rechnen das totale Dierential
(9.108)
dS = T1 dU + PT dV
von den Variablen U , V auf T , P um:
dS = T1 [( @U
)P + P ( @V )P ]dT + 1 [( @U )T + P ( @V )T ]dP:
(9.109)
@T
@T
T @P
@P
Wir ersetzen in der ersten [..]:
(9.110)
( @U )P + P ( @V )P = CP
@T
@T
und bringen die zweite [..] mit Hilfe der Integrabilitatsbedingung
1 @ [( @U ) + P ( @V ) ] = @ f 1 [( @U ) + P ( @V ) ]g
(9.111)
T @P @T P
@T P T @T T @P T
@P T P
auf die gewunschte Form:
1 ( @V ) = , 1 [( @U ) + P ( @V ) ];
(9.112)
T @T P
T 2 @P T
@P T
alle restlichen Terme in (9.111) heben sich fort. Da fur einen adiabatischen Proze dS = 0,
folgt aus (9.109) mit (9.110) und (9.111):
CP dT = ( @V ) dP; q:e:d:
(9.113)
T
@T P
In einem zweiten Schritt beweisen wir, da der Quotient (@V=@T )P =CP fur T ! 0 endlich
bleibt. Daraus folgt dann in (9.107), da die gleiche Druckanderung mit abnehmender
89
Temperatur eine immer kleinere Temperatur-A nderung bewirkt. Da wir wissen, da CP !
0 fur T ! 0, konnen wir fur kleine Temperaturen schreiben
CP = T (a + bT + :::)
wobei > 0 und a; b Funktionen von P sind. (@V=@T )P konnen
verknupfen:
Z T
Z T
@S
@
C
@V
P
0
( )P = ,( )T = ,
dT
= , @CP
0
@T
@P
@P 0 T
@P
0
wenn wir (9.112) in (9.109) einsetzen. Mit
@CP = T (a0 + b0 T + :::)
@P
wird nach Ausfuhrung des Integrals in (9.115):
0
0
( @V )P = ,T ( a + b T + :::);
@T
+1
(9.114)
wir wie folgt mit CP
1 dT 0;
T0
(9.115)
(9.116)
(9.117)
also
a0 : endlich:
( @V
)
=C
=
,
(9.118)
@P P P
a
Das Ergebnis veranschaulicht die folgende (schematische) Darstellung von S = S (T; P ) :
Durch eine Folge isothermer und adiabatischer Druckanderungen kann man die Temperatur erniedrigen; da aber nach dem 3. Hauptsatz S (T; P ) = S (T; P 0) fur T = 0 ist,
erreicht man den absoluten Nullpunkt nicht mit endlich vielen Schritten bei endlicher
Druckdierenz. Analogie: Magnetische Kuhlung (vgl. Teil III).
90
9.10 Das klassische ideale Gas
erlaubt in einfacher Weise die konkrete Auswertung der vorangegangenen U berlegungen.
Zunachst wollen wir uns die ideale Gas-Gleichung verschaen. Nach der Tabelle (*) konnen
wir den Druck P berechnen als
@J )
(9.119)
P = ,( @V
T;
mit
J = U , TS , N = J (T; V; ):
(9.120)
Dies ist gerade das zur grokanonischen Gesamtheit passende thermodynamische Potential, also:
1 ln Z = ST , U + N = ,J
(9.121)
g
nach Gleichung (7.38). ln Zg konnen wir aber aus (8.16) bzw. (8.17) im klassischen Grenzfall berechnen:
X
X
ln Zg = lnf1 exp(,i , )g exp(,i , ) = exp(,) V3 (2s + 1): (9.122)
i
i
Also wird
oder schlielich,
@J ) = 1 exp(,) 2s + 1 = N k T
P = ,( @V
T;
3
V B
(9.123)
PV = N kB T:
(9.124)
Aus der inneren Energie U = 3=2N kB T (8.30) folgt sofort:
(9.125)
CV = 23 N kB ;
im oensichtlichem Widerspruch zum 3. Hauptsatz: => die klassische Naherung ist
bei tiefen Temperaturen unbrauchbar! CP folgt aus (9.98) mit (8.30) und (9.124)
CP = CV + N kB :
91
(9.126)
Kapitel 10
Kleine Abweichungen vom
Gleichgewicht
10.1 Einfuhrung
Wir wollen im folgenden zwei Dinge untersuchen, die auf den ersten Blick scheinbar nichts
miteinander zu tun haben: spontane Schwankungen (Fluktuationen) physikalischer
Groen um ihren Mittelwert im statistischen Gleichgewicht und erzwungene Abweichungen vom Mittelwert bei Storungen des Gleichgewichts durch auere Eingrie.
Es wird sich zeigen, da diese beiden Dinge eng miteinander verknupt sind bei schwachen aueren Eingrien und im Fluktuations-Dissipations-Theorem ihren Ausdruck
nden.
10.2 Fluktuationen
In Kap. 5 hatten wir die fundamentale Annahme gemacht, da makroskopische Daten
eines physikalischen Systems in Form von Mittelwerten uber die das System reprasentierende statistische Gesamtheit berechnet werden konnen. Als Ma fur die Gute dieser
Naherung kann man die relative quadratische Schwankung
A
(10.1)
<A>
bei
(A)2 =< A2 > , < A >2
(10.2)
betrachten. Schwankungen hoherer Ordnung werden nur in seltenen Fallen benotigt. Als
zwei wichtige konkrete Falle betrachten wir Energie- und Konzentrationsschwankungen.
Fur die innere Energie U einer kanonischen Gesamtheit hatten wir gefunden
exp(,H )) :
(10.3)
U = SpSp(H(exp(
,H ))
92
Die gesuchte mittlere quadratische Schwankung erhalten wir durch Dierenziation von
(10.3) nach :
@U = , Sp(H 2 exp(,H )) + [Sp(H exp(,H ))]2 = , < H 2 > + < H >2= ,(H )2
@
Sp(exp(,H ))
[Sp(exp(,H ))]2
(10.4)
also
(H )2 = , @U
(10.5)
@ :
Daraus wird mit (9.97)
2
[ H ]2 = kB T 2CV :
(10.6)
<H>
U
Nun wachsen U und CV als extensive Groen | im Gegensatz zu T | linear mit der
Teilchenzahl N ; die relative Schwankung hangt also gema
H p1
(10.7)
<H>
N
von der Teilchenzahl ab, so da bei groen Systemen die Energieschwankungen gegenuber
der Gesamtenergie vernachlassigbar sind, wenn man sich nicht in unmittelbarer Nahe
eines Phasenuberganges bendet, wo CV singular werden kann.
Beispiel: Fur das ideale klassische Gas hatten wir gefunden
< H >= U 23 N kB T;
(10.8)
so da
H = 2 p1 :
(10.9)
<H >
3 N
Analog berechnet sich die mittlere quadratische Schwankung der Teilchenzahl in der grokanonischen Gesamtheit aus
^
^
< N^ >= Sp(N exp(,^N , H )) ;
(10.10)
Sp(exp(,N , H ))
es wird entsprechend (10.5):
^
(N^ )2 = , @ <@N > :
(10.11)
Analog (10.6) lat sich N^ mit Hilfe der isothermen Kompressibilitat T =: ,1=V (@V=@P )T
ausdrucken. Es ist (Beweis siehe unten)
N2 ( @N
)
(10.12)
T =
@
V T
oder mit = ,
(N^ )2 = kB T T :
(10.13)
N2
V
s
93
Da V eine extensive Groe ist, T und T jedoch intensive Groen, bleibt (N =:< N^ >)
N^ p1 :
(10.14)
N
< N^ >
Erganzung: (Beweis von Gleichung (10.12))
Fur homogene Systeme gilt fur extensive Groen wie z:b. die mittlere Energie U =
U (S; V; N ) :
U = U (S; V; N );
(10.15)
da auch S; V; N extensiv sind. Ist speziell = 1 + , jj 1, so folgt durch TaylorEntwicklung in (10.15):
(1 + )U = U + (S [ @U ]V;N + V [ @U ]S;N + N [ @U ]S;V ):
(10.16)
@S
@V
@N
Vergleich der Faktoren von ergibt
U = TS , PV + N;
(10.17)
wenn man Fall V aus der Tabelle (*) beachtet. Vegleicht man das totale Dierential von U
gema (10.17) mit dem Ergebnis von Tabelle (*), so bleibt die Gibbs-Duhem-Relation:
SdT , V dP + N d = 0:
(10.18)
(Da in (10.18) T; P; die naturlichen Variablen sind, haben wir Volumen und Teilchenzahl
als Mittelwerte V , N geschrieben.) Fur isotherme, quasistatische Prozesse folgt:
V dP = N d
oder
(10.19)
V ( @@NP )T = N ( @@N )T :
(10.20)
Da P in homogenen Systemen auer von T nur noch von der Dichte N =V abhangt, ist
aber
V ( @@PV )T = ,N ( @@NP )T ;
(10.21)
@V ) = V ( @N ) :
(10.22)
T =: , V1 ( @P
T
N 2 @ T
Als Beispiel fur Formel (10.13) betrachten wir ein ideales klassisches Gas mit PV =
N kB T . Dann wird:
T = P1 ;
(10.23)
so da
(N^ )2 = kB T = 1 :
(10.24)
N 2 (P V ) N
Ergebnis: Fur makroskopische Systeme sind die Fluktuationen von Energie und Teilchenzahl vernachlassigbar gegenuber der Energie und Teilchenzahl des Systems.
94
Daher ist es fur makroskopische Systeme praktisch bedeutungslos, ob man ein System
durch die mikrokanonische, die kanonische oder die grokanonische Gesamtheit beschreibt,
solange man sich nur fur Aussagen uber das System im Gleichgewicht interessiert. Die
Wahl der das System beschreibenden Gesamtheit kann dann unter dem Gesichtspunkt der
bequemeren Rechentechnik erfolgen. Wichtig dagegen sind die Fluktuationen, wenn man
kleine Abweichungen vom Gleichgewicht durch auere Eingrie betrachtet. Beispiele dafur
sind die Gleichungen (10.6) und (10.13), in denen die spezische Warme bzw. die isotherme
Kompressibilitat mit den Fluktuationen von Energie und Teilchenzahl verknupft sind.
Spezische Warme und Kompressibilitat charakterisieren aber die Reaktion des Systems
auf aueren Eingri in Form von Warmezufuhr bzw. Druck.
Wir wollen nun den Zusammenhang von Fluktuationen und der Reaktion des Systems
auf (schwache) auere Eingrie allgemein untersuchen.
10.3 Thermodynamische Storungstheorie
Wir betrachten zunachst den Fall einer zeitunabhangigen Storung. Dabei zerlegen wir den
gesamten Hamiltonoperator
H = H0 + W;
(10.25)
wo H0 exakt behandelt werden kann und W eine kleine zeitunabhangige Storung ist. Wir
beschreiben das System als kanonische Gesamtheit. Dann ist es zweckmaig, von dem
Operator exp(, H ) den Faktor exp(, H0) abzuspalten, der ja nach Voraussetzung
exakt behandelt werden kann. Also:
expf, [H0 + W ]g = expf,H0g ( ):
(10.26)
Zur Bestimmung von ( ) dierenziert man (10.23) nach und erhalt:
@ : (10.27)
,[H0 + W ] expf, [H0 + W ]g = ,H0 expf,H0g( ) + expf,H0 g @
Nach Einsetzen von (10.26) in (10.27) entsteht die sogenannte Bloch-Gleichung
@ = ,W ( )( )
(10.28)
@
mit der Abkurzung
W ( ) = expfH0g W expf,H0 g:
(10.29)
Die Bloch-Gleichung ist formal analog zum Dirac-Bild der Quantentheorie aufgebaut.
Dementsprechend kann man die Dirac0sche Storungstheorie formal ubertragen: Man
uberfuhrt (10.28) mit der aus (10.26) folgenden Randbedingung
(0) = 1
(10.30)
in eine Integral-Gleichung
( ) = 1 ,
Z
0
W ( 0)( 0)d 0;
95
(10.31)
die man iterativ lost:
( ) = 1 ,
Z
0
W ( 0)d 0 +
Z
W ( 0)
0
Z
0
0
W ( 00)d 00d 0 , ::::
(10.32)
Zur Berechnung der kanonischen Zustandssumme Zk benutzen wir die Basis der Eigenzustande ji > von H0 mit den Energien i;
exp(,i )( )ii:
(10.33)
Wir benotigen also die Diagonalelemente von ( ) in der Basis der Eigenzustande von
H0. Dafur erhalt man aus (10.32):
Zk =
X
i
< i j expf,H0 g( )ji >=
( )ii = 1 , Wii + 21 2jWiij2 ,
X
i
exp(,i) < ij( )ji >=
X
i
f (i , j )g] ::: (10.34)
jWij j2f ( , ) + [1 , exp
(i , j )2 g
i
j
j 6=i
X
Dabei wurde die Vollstandigkeit der Eigenzustande ausgenutzt in:
Z
(
=
X
j
jWij j
2
Z
0
0
W ( 0)
Z
0
0
W ( 00)d 00d 0)ii
Z 0
exp( (i , j ))
0
0
(10.35)
exp( 00(j , i ))d 00d 0;
die verbleibenden Integrale sind trivial. Bei der Berechnung von Zk mit (10.34) fallt der
letzte Term von (10.34) exakt weg, da i, j die gleichen Werte durchlaufen und W = W y
gilt,
X
f (i , j )g] 0:
jWij j2 exp(,i) [1 , exp
(10.36)
( , )2
Es bleibt
i
i6=j
j
X jW j2
1
2
2
Zk = exp(,i)[1 , Wii + 2 jWiij , ( ,ij ) :::]
j
i
j 6=i i
oder mit den Abkurzungen
X
,i )
Zk0 = exp(,i); pi = (Pexp(
j exp(,j ))
i
X
(10.37)
(10.38)
eine fur die weitere Auswertung ubersichtlichere Form:
Zk = Zk0[1 , X
i
Wii pi + 21 2 fWii2 pi ,
X
i
jWij j2 (pi , pj ) g:
(i , j )
j 6=i
X
(10.39)
Der in W lineare Term ist gerade der Mittelwert von W in der durch H0 beschriebenen
Gesamtheit,
X
< W >0= pi Wii:
(10.40)
i
96
Zur Auswertung der restlichen Terme in (10.39) wollen wir die (in vielen praktischen
Fallen gut erfullte) Annahme (i , j ) 1 machen, so da
i ) , exp(,j )
pi , pj = exp(,exp(
, ) = pi(1 , exp[ (i , j )]) ,pi (i , j ); (10.41)
P
k
k
so da
jWij j2(pi , pj ) , p jW j2:
i ij
j 6=i [ (i , j )]
j 6=i
X
X
(10.42)
Nun ist aber aufgrund der Vollstandigkeit der Eigenzustande ji > zu H0 :
< i jW 2ji >=
X
j
< i jW jj >< j jW ji >= Wii2 +
X
j 6=i
jWij j2:
(10.43)
Damit erhalt (10.39) die ubersichtliche Form:
Zk = Zk0[1 , < W >0 + 21 2 < W 2 >0 :::]
(10.44)
und die freie Energie F = ,kB T ln Zk erhalt die Form
(10.45)
F = F 0 + < W >0 , 21 (< W 2 >0 , < W >20)::::
Wir konnen also die durch die Storung W bedingten Korrekturen zur freien Energie ausdrucken durch den Mittelwert von W und seine quadratische Schwankung im ungestorten
Gleichgewicht, beschrieben durch den statistischen Operator exp(,H0):
Wir wenden den obigen Formalismus an auf den Fall, da an einer Observablen q des
Systems (z:B . magnetisches Momemt oder elektrische Stromdichte) eine auere Kraft
f (z:B . ein homogenes magnetisches oder elektrisches Feld) angreift, und fragen, wie sich
(kleine) A nderungen von f auf das System auswirken. Wir setzen also in (10.25)
H0 = Hs , qf ;
W = ,q f:
(10.46)
Das zugehorige thermodynamische Potential ist die freie Enthalpie G, die sich von F durch
die von der aueren Kraft herruhrende potentielle Energie unterscheidet. Entsprechend
(10.45) erhalt man
G = G0 , < q >0 f , 21 (f )2:::;
(10.47)
wobei die verallgemeinerte Suszeptibilitat ist,
= < (q, < q >0)2 >0 = < q2 >0 ;
(10.48)
beschrieben durch die mittlere quadratische Schwankung von q der ungestorten Gleichgewichtsgesamtheit.
97
10.4 Linear-Response
Wir wollen nun untersuchen, welche A nderungen der Mittelwert einer Observablen < q >
erleidet, wenn an q eine zeitabhangige Kraft f (t) angreift. Beispiele: Stromdichte unter
Einu eines zeitabhangigen elektrischen Feldes; magnetisches Moment unter Einu eines
zeitabhangigen Magnetfeldes. Dann ist in
< q(t) >= Sp(q (t))
(10.49)
der statistische Operator zu bestimmen aus (vgl. Gl. (5.4)):
@ = , i [H , q f (t); (t)];
(10.50)
@t
h 0
wenn H0 der vollstandige Hamiltonoperator des Systems ohne auere Kraft ist.
Zur naherungsweisen Berechnung von (10.49) geht man uber ins Dirac-Bild:
q(t) = expf hi H0tg q expf, hi H0 tg;
(10.51)
(10.52)
(t) = expf hi H0tg (t) expf, hi H0tg;
und erhalt
< q(t) >= Spfq(t)(t)g;
(10.53)
dabei gehorcht (t) der Dierentialgleichung
@ (t) = i [q(t); (t)] f (t);
(10.54)
@t
h
wenn man f (t) klassisch behandelt. Als Anfangsbedingung wollen wir verlangen, da
das System vor Einschalten der Storung f (t) sich im thermischen Gleichgewicht bei der
Temperatur T bendet,
,H0) :
(,1) = (,1) = 0 = Spexp(
(10.55)
(exp(,H0))
Fur hinreichend schwache Krafte f (t) kann man sich auf die beiden ersten Terme der
Storungstheorie beschranken,
Z t
(t) = 0 + hi
[q(t0); 0 ]f (t0)dt0:::;
(10.56)
,1
und bekommt mit
Spfq(t)0q(t0)g = Spfq(t0)q(t)0g
(10.57)
(zyklische Invarianz der Spur) fur den gesuchten Mittelwert
Z 1
i
< q(t) >=< q >0 + h
(t , t0 ) < [q(t); q(t0)] >0 f (t0)dt0:
(10.58)
,1
98
bezeichnet die Sprung-Funktion:
(t , t0) = 1 falls t t0; (t , t0) = 0 sonst:
(10.59)
Man nutzt nun aus, da die ungestorte Gesamtheit 0 stationar ist,
< [q(t); q(t0)] >0 =< [q(t , t0); q(0)] >0 ;
(10.60)
und geht in (10.58) zur Fourier-Darstellung uber. Man fuhrt dazu ein:
q! =:
1
(< q(t) > , < q >0) exp(i!t)dt;
,1
Z 1
f! =:
f (t) exp(i!t)dt
,1
iZ1
Z
(10.61)
(10.62)
< [q(t); q(0)] >0 exp(i!t)dt
(10.63)
r(!) =: h
0
und erhalt mit diesen Bezeichnungen nach Multiplikation von (10.58) mit exp(i!t) und
Integration [,1, 1]:::dt die aquivalente Beziehung
q! = r(!) f! :
(10.64)
r(!) heit die Response-Funktion des Systems, die wir im folgenden etwas naher untersuchen wollen.
Anmerkung zum U bergang (10.58) ! (10.64) (Faltungstheorem).
Setzt man (10.60) in (10.58) ein, so erhalt man ein Faltungsintegral vom Typ:
a(t) =
Z
1
b(t , t0)c(t0 ) dt0:
,1
(10.65)
Nach einer Fourier-Transformation der Groen a(t), b(t) und c(t) erhalt man fur die
Fourier-Transformierten a! , b! und c! die einfache algebraische Relation (U B)
a! = b! c! :
(10.66)
Von diesem Faltungstheorem wurde beim U bergang von (10.58) zu (10.64) implizit Gebrauch gemacht. Hinsichtlich der Integrationsgrenzen in (10.63) ist zu bemerken, da
( =: t , t0 ) :
Z
1
< [q( ); q(0)] >0 exp(i! )( )d
,1
=
1
Z
0
< [q( ); q(0)] >0 exp(i! )d:
(10.67)
10.5 Beispiele
Um die Rolle der Response-Funktion r(!) zu veranschaulichen, seien einige einfache Beispiele betrachtet.
99
1. Die Bewegungsgleichungen eines gedampften harmonischen Oszillators unter dem Einu einer aueren Kraft lauten:
2
(10.68)
m( dtd 2 q + !02q) + dtd q = f (t):
Nach Fourier-Zerlegung von q(t) und f (t) wird daraus
fm(!02 , !2) , i!gq! = f! ;
(10.69)
oder nach Vergleich mit (10.64)
r(!) = m(!2 , !12) , i ! :
0
(10.70)
2. Bei der Brown'schen Bewegung untersuchen wir die Bewegung makroskopischer
Partikel (z:B . Staubteilchen) in einem Gas oder einer Flussigkeit aufgrund der thermischen Bewegung der Molekule des Gases bzw. der Flussigkeit, die mit den makroskopischen Teilchen zusammenstoen. Die auf ein makroskopisches Teilchen wirkende Kraft
teilt man auf in eine Reibungskraft und eine stochastische Kraft, deren zeitlicher
Mittelwert verschwindet:
2
(10.71)
m dtd 2 q + dtd q = f (t)
mit dem zeitlichen Mittelwert von f (t)
f = 0:
(10.72)
Fur diesen Fall wird analog Beispiel 1.
r(!) = ,m!21, i ! :
3. Wir betrachten ein einfaches Beispiel fur das Widerstandsrauschen:
(10.73)
Ein Stromkreis enthalte eine Kapazitat C und einen Ohm'schen Widerstand R, der auf
einer Temperatur T durch ein Warmebad gehalten werde (Skizze).
100
Herrscht an den Enden des Widerstandes R die Spannungsdierenz U , so iet im Stromkreis der Strom J = U=R. Nun mussen wir allerdings noch beachten, da die den Strom
tragenden Elektronen zusatzlich der thermischen Bewegung unterworfen sind: sie werden
in unregelmaiger Weise von den Atomen des Leiters gestreut. Daher wird der Strom
uktuieren um den Mittelwert U=R. Fur den wirklichen Verlauf des Stromes erwarten wir
also
U =J +J ;
(10.74)
th:
R
wobei Jth: von der thermischen Bewegung der Elektronen bei der Temperatur T herruhrt;
Jth: hat also mit der Spannung U nichts zu tun. U ber den Zusammenhang des Stroms mit
der zeitlichen A nderung der Ladung Q;
J = , dtd Q = ,C dtd U;
(10.75)
erhalt man
U + RC dtd U = Uth:
(10.76)
mit der ktiven Spannung
Uth: = R Jth:
(10.77)
Nach Fourier-Zerlegung von U und Uth: folgt
(1 , i!RC )U (!) = Uth:(!)
(10.78)
und durch Vergleich mit (10.64)
1 :
r(!) = 1 , i!RC
(10.79)
In allen drei Beispielen kommt die Statistik nur pauschal ins Spiel durch die Reibung
bzw. den Widerstand R; daher gelingt es auch auf so einfache Weise, die ResponseFunktion r(!) zu ermitteln.
10.6 Fluktuations-Dissipations-Theorem
Wir wollen nun den eingangs behaupteten Zusammenhang von Fluktuationen im Gleichgewicht mit erzwungenen Abweichungen vom Gleichgewicht aufgrund zeitabhangiger Storungen beweisen. Das Ergebnis wird eine einfache Beziehung sein zwischen den Fluktuationen der Observablen, an der die Storung angreift, und dem dissipativen Anteil der
Response-Funktion r(!), der fur die Umwandlung der von der aueren Kraft am System geleisteten Arbeit in innere Energie verantwortlich ist.
Zu diesem Zweck fuhren wir die Spektralfunktion s(!) ein durch
Z 1
s(!) = 2h
< q(t)q(0) >0 exp(i!t) dt:
(10.80)
,1
101
s(!) ist eine reelle Funktion, d.h. s(!) = s(!). Zum Beweis bilden wir < q(t)q(0) >0 in
der Energie-Darstellung,
f,i g
s(t) = h1 < q(t)q(0) >0= h1 ( expexp(
,k )) j < i jq(t)jj >< j jqji > (10.81)
k
i
X
X
P
X
f,i g j < jqj > j2 exp( i [ , ]t):
= h1 (Pexp
i
j
exp(, ))
h i j
i;j
k
k
Die t-Integration in (10.80) liefert dann gerade die -Distribution vom Argument (h! +
i , j ), also schlielich
X
,i) 0
(10.82)
s(!) = j < i jqjj > j2 (h! + i , j ) Pexp(
k exp(,k )
i;j
und reell wie behauptet. Es folgt direkt eine weitere zum Beweis des Fluktuations-Dissipations-Theorems notwendige Relation,
s(,!) = exp(, h !)s(!):
(10.83)
Zum Beweis beachte man, da
(,h ! + i , j ) = (h! + j , i );
(10.84)
sowie da j < i jqjj > j2 bzgl. i, j symmetrisch ist und da wegen der Anwesenheit der
-Distribution
exp(,i ) ! exp[, (j + h !)]
(10.85)
ersetzt werden kann.
Wir benotigen nun noch den Zusammenhang von s(!), s(,!) mit der ResponseFunktion r(!). Letztere zerlegen wir in Real- und Imaginaranteil
r(!) = d(!) + i a(!);
(10.86)
wobei d(!) der dispersive, a(!) der absorptive Anteil heit (Erlauterung siehe weiter
unten). Benutzt man (10.63), so wird
1
a(!) = 21i (r(!) , r(!)) = 21h
< [q(t); q(0)] >0 exp(i!t)dt = s(!) , s(,!);
,1
(10.87)
wenn man beachtet:
< q(t)q(0) >0 =< q(0)q(,t) >0
(10.88)
aufgrund der Invarianz gegen Zeittranslation bei der Spurbildung in der stationaren Gesamtheit 0 . Aus (10.86) und (10.83) wird nun
a(!) = s(!)[1 , exp(, h !)]
(10.89)
und
s(!) + s(,!) = s(!)[1 + exp(, h !)];
(10.90)
Z
102
deren Kombination das allgemeine Fluktuations-Dissipations-Theorem ergibt:
h !
h [s(!) + s(,!)] = a(!) [ h ! +
(10.91)
2
! 2 (exp( h !) , 1) ]:
Auf der linken Seite von (10.91) steht die Fourier-Transformierte der Schwankungsgroe
(beachte, da q(0) q und < f (q(t)) >0 =< f (q) >0 ))
< q(t)q + qq(t) >0 2 < q2 >0 , < (q(t) , q)2 >0 :
(10.92)
Auf der rechten Seite steht der dissipative Anteil der Response-Funktion r(!), -abgesehen
von temperatur- und frequenzabhangigen Termen. | Wir mussen uns noch uberzeugen,
da a(!) mit dem dispersiven Anteil zu identizieren ist.
Dazu untersuchen wir die von der aueren Kraft f (t) am System geleistete Arbeit, die
der inneren Energie des Systems zugute kommt. Wir bilden
d < H >= Sp(H_ ) = , i Sp([H , f (t)q; ]H )
(10.93)
0
0
0
0
dt
h
= , hi Sp([H0; H0 , f (t)q]) = hi Sp([H0; q]f (t)(t)) =< q_ > f (t);
daraus ergibt sich die insgesamt an das System abgegebene Energie nach t-Integration
1
< q_ > f (t)dt
(10.94)
,1
Z 1 Z 1
Z 1
i
i
=,
! q exp(,i!t)f (t)dt d! = , 2
! q! f,! d!
2 ,1 ,1 !
,1
Z 1
i Z 1 !jf j2r(!) d! = Z 1 !jf j2a(!)d! > 0;
!
q
=, i
! f! d! = ,
!
2 ,1
2 ,1 !
0
< H0(1) > , < H0 (,1) >=
Z
wenn man beachtet
f! = f,! ;
da f (t) reell ist, sowie die Tatsache (folgt direkt aus (10.63) und (10.88)), da
r(!) = r(,!):
(10.95)
(10.96)
Wegen
d(!) = d(,!); a(!) = ,a(,!)
(10.97)
tragt nur a(!) zum Integral (10.94) bei; die gerade Funktion liefert nach Multiplikation
mit !jf! j2 keinen Beitrag (ungerader Integrand).
Als ein instruktives Beispiel fur das Verstandnis von Real- und Imaginar-Teil der ResponseFunktion r(!) sei der Brechungsindex einer Substanz erwahnt: Der Realteil des Brechungsindex gibt an, wie ein Lichtstrahl beim U bergang Vakuum-Substanz gebrochen
wird; diese Brechung ist im allgemeinen frequenzabhangig: die Substanz zeigt Dispersion. Daher bezeichnet man den Realteil von r(!) generell als den dispersiven Anteil.
103
Beim Durchgang durch die Substanz wird der Lichtstrahl auerdem in seiner Intensitat
geschwacht, die Substanz absorbiert Strahlungsenergie. Diese Absorption ist ebenfalls
frequenzabhangig und wird durch den Imaginaranteil des Brechungsindex beschrieben.
Im klassischen Grenzfall h ! kB T wird
(1 + exp(, h !)) a(!) 2 kB T ;
(10.98)
s(!) + s(,!) = a(!) (1
, exp(, h !))
h !
so da (10.91) die Form annimmt
h (s(!) + s(,!)) = a(!) k T:
(10.99)
2
! B
10.7 Verallgemeinerung des klassischen Gleichverteilungssatzes
Aus (10.91) folgt durch Integration uber !
Z 1
2 a(!!) f h2! + exp(hh!!) , 1 gd!
0
= h
=
(nach (10.80))
=
Z
Z
0
1
fs(!) + s(,!)gd! = h
(10.100)
1
s(!)d!
,1
Z
1Z1
< q(t)q(0) >0 exp(i!t) d!
2 dt
,1 ,1
Z
1
< q(t)q(0) >0 (t)dt =< q(0)2 >0=< q2 >0 :
,1
Eine entsprechende Relation erhalt man fur den Mittelwert der zu q kanonisch konjugierten Variablen p. Zu ihrer Herleitung benutzen wir:
< i jq_(t)jj >= hi < i j[H0; q(t)]jj >= hi (i , j ) < ijq(t)jj >;
(10.101)
woraus durch Iteration folgt
2
< i j dtd q_(t)jj >= , (i ,2j ) < i jq(t)jj > :
(10.102)
h
Mit (10.81) folgt
2
exp(,i)
d2 s(t) = , 1 P
i;j
2 (i , j )
expf i (i , j )tg (10.103)
j
<
ijqjj > j
P
2
2
dt
h ( k exp(,k ))
h
h
P
exp(, )
1
= , h (Pi;jexp(, i)) j < i jq_jj > j2 expf hi (i , j )tg
k
k
104
= , h1 < q_(t)q_(0) >0
P
exp(,i )
1
= Pi;j
<
i j d q_jj >< j jqji > expfi=h (i , j )tg
h ( k exp(,k ))
dt
P
,i ) < j d q_(t)qj >= 1 < d q_(t)q(0) >
= h1 (P i exp(
i
i
0
dt
hbar dt
k exp(,k ))
und (10.80) (nach partieller Integration)
!2s(!) = , 21h
1
< ( dtd q_(t))q(0) >0 exp(i!t)dt:
,1
Z
Durch Integration uber ! gema (10.100) erhalten wir
Z 1
Z 1
h
!2s(!)d! = 2 ! a(!)f h2! + exp(hh!!) , 1 gd!
,1
0
=< q_2 >0 =:< p2 >0 =m2 ;
wenn man nach (10.103) beachtet
d q_(t))q(0) > = , < q_2 > :
lim
<
(
0
0
t!0
dt
Die Relationen
< q2 >0= h
Z 1
1
s(!) d! = 2 q(!!) f h2!
,1
0
Z
+ (exp(hh!!) , 1) g d!
(10.104)
(10.105)
(10.106)
(10.107)
und
h !
< p2 >0 = h 1 !2s(!) d! = 2 1 ! a(!)f h ! +
(10.108)
2
m
2 exp( h !) , 1 g d!
,1
0
kann man als quantenmechanische Verallgemeinerungen des Gleichverteilungssatzes ansehen.
Um uns davon zu uberzeugen, benutzen wir fur h ! kB T
a(!) s(!) kh !T = s(!) h !
(10.109)
B
aus (10.89) sowie
f h2! + (exp(hh!!) , 1 g kB T = ,1
(10.110)
Z
Z
entsprechend (10.98). Damit wird
h
Z 1
1 2
! s(!) d! 2 kB T !
,1
0
Z
a(!)d! = 2 kB T
= 2 kB T
1
!
,1
Z
105
1
Z
0
s(!) d!;
!(s(!) , s(,!)) d!
(10.111)
wenn man (10.87) einsetzt. Nun ndet man entsprechend den obigen Rechnungen zu
(10.107) bzw. (10.108)
Z
1
!
,1
s(!)d! = hi < [p;2mq] >0 = 21m
(10.112)
fur kanonisch konjugierte Variable. Also wird
< p2 >0 = 1 k T;
(10.113)
2m
2 B
wie es der Gleichverteilungssatz behauptet. Der Beweis der entsprechenden Aussage fur
< q2 >0 ist aufwendiger und wird hier nicht explizit vorgefuhrt.
10.8 Beispiele
Zur Veranschaulichung des Fluktuations-Dissipations-Theorems kommen wir noch einmal
auf das Widerstandsrauschen zuruck. Aus (10.79) folgt sofort
a(!) = 1 (1 +!RC
(10.114)
! 2 R2 C 2 ) ;
so da bei der klassischen Naherung h ! kB T nach (10.99)
h [s(!) + s(,!)] = 1 kB T RC :
2
(1 + !2R2C 2)
(10.115)
Bei der Interpretation der linken Seite von (10.115) ist zu beachten, da q f (t) eine
Energie sein mu und q eine zeitabhangige klassische Groe ist. Da Gleichung (10.79)
eine Identikation von f (t) und Uth: (t) impliziert, entspricht q der Ladung Q(t) = C U (t).
Auf der linken Seite der Nyquist-Formel (10.115) steht also die Fourier-Transformierte
der Schwankung der Ladung. Will man zur Spannung ubergehen, so ist (10.79) mit 1=C
zu multiplizieren und in (10.114) und (10.115) entfallt auf der rechten Seite der Faktor C
im Zahler. Integriert man die so entstehende Gleichung (10.115) analog (10.100) uber !,
so wird
Z 1
2
kB T R d!
2
(10.116)
< U (t) >0 = 0 (1 + ! 2 R2 C 2 )
Z
2
k
kB T
BT 1 1
= C
dx
=
(10.117)
2
1+x
C
0
fur x = !RC . < U (t)2 >0 ist also unabhangig von R; bei kleineren R-Werten wird in
(10.116) der Beitrag kleiner Frequenzen zwar geringer, dafur tragen aber hohere Frequenzen noch zum Integral bei.
106
Teil III
Anwendungen der Statistischen
Mechanik
107
Kapitel 11
Das ideale Fermi-Gas
Die Quantenmechanik von Fermi-Systemen wurde in Kap. 2 behandelt und in Kap. 8 fur
den Fall unabhangiger Fermionen benutzt als ein Anwendungsbeispiel fur die grokanonische Gesamtheit. Die Ergebnisse des Kap. 8 sollen nun im einzelnen diskutiert werden
und auf konkrete physikalische Probleme angewendet werden (Spezische Warme von
Metall-Elektronen bei tiefen Temperaturen, Gluhemission von Elektronen aus Metallen).
11.1 Fermi-Verteilung
Fur die mittlere Besetzungszahl des Einteilchenniveaus i hatten wir gefunden
< ni >= exp( [ 1, ]) + 1 ;
i
(11.1)
wobei = 1=(kB T ) und das chemische Potential ist. Fur den Grenzfall hoher Temperaturen (oder geringer Dichte) hatten wir in Kap. 8.4 schon gefunden, da < ni >
exponentiell mit der Energie abfallt,
< ni > exp(, [i , ])
(11.2)
fur V=N (2mkB T=h2)3=2 1. Im anderen Grenzfall niedriger Temperaturen (T ! 0,
! 1) mussen wir unterscheiden i > und i < . Fur i > und ! 1 gilt
oensichtlich < ni >! 0 exponentiell, dagegen wird < ni >! 1 fur i < und ! 1.
Fur i = nimmt < ni > den Wert 1=2 an; damit erhalt eine anschauliche Bedeutung:
T =0 gibt die Energie an, bis zu der die Einteilchen-Niveaus am absoluten Nullpunkt
voll besetzt sind; fur Energien oberhalb T =0 sind alle Zustande leer. T =0 =: F nennt
man entsprechend dem Verhalten von < ni > (siehe Skizze) die Fermi-Kante; sie ist
bestimmt durch die Forderung
X
< ni >= N ;
(11.3)
i
wobei N die vorgegebene mittlere Teilchenzahl des Systems ist. Die Fermi-Kante hangt
also von der Teilchenzahl des Systems ab. Die bei T = 0 scharfe Fermi-Kante weicht bei
T 6= 0 auf.
108
Fermi-Verteilung als Funktion der Einteilchenenergie fur T = 0 und T > 0.
11.2 Innere Energie und Teilchenzahl bei niedrigen
Temperaturen T = 0:
6
Bei der Berechnung von
N=
und
U=
ersetzen wir (vgl. Kap. 8.4)
X
i
X
i
< ni >
(11.4)
i < ni >
(11.5)
(11.6)
:::: ! (2V)3 d3k:::::
k
Da die uns interessierenden Groen (11.4) und (11.5) im nicht-relativistischen Limes nur
von
2 2
h
= 2mk
(11.7)
abhangen, rechnen wir um
d3 k::: = 4 k2 dk::: = 2( 2m2 )3=2 1=2 d:::
(11.8)
h
Die uns interessierenden Integrale sind dann von der Form
1
)
d
(11.9)
I = C expf( , f()=k
0
BT g + 1
mit (s bezeichne den Spin der Teilchen)
C = (2s + 1) 2( 2m2 )3=2 :
(11.10)
h
Fur die Berechnung von N ist f () = 1=2 , fur U entsprechend f () = 3=2 : Zur Berechnung
des Integrals (11.9) fur niedrige Temperaturen substituieren wir
, = kB T z;
(11.11)
Z
X
Z
Z
Z
Z
109
so da (Konstante C aus (11.9) weggelassen)
f ( + kB Tz) dz
exp(z) + 1
,1
=(kB T ) f ( , kB Tz )
1 f ( + kB Tz )
= kB T f
dz
+
exp(,z) + 1
exp(z) + 1 dzg:
0
0
Mit der Identitat
1
1
=1,
exp(,z) + 1
exp(z) + 1
Z
kB T
=kB T
Z
(11.12)
Z
(11.13)
konnen wir (11.9) in einen T = 0-Beitrag und eine Korrektur fur T 6= 0 aufspalten:
Z
0
f () d + kB T
1 [f ( + kB Tz ) , f ( , kB Tz )]
Z
exp(z) + 1
0
dz;
(11.14)
wobei im 2. Term fur =(kB T ) 1 die obere Integrationsgrenze nach 1 verschoben
werden kann. Entwickelt man im 2. Term den Zahler im Integranden nach Potenzen von
z, so wird
Z 1
Z 2 0
I = C f f () d + 2(kB T ) f () exp(zz) + 1 dz
(11.15)
0
0
Z 1
3
1
4 000
+ 3 (kB T ) f () exp(zz) + 1 dz + :::g;
0
alle geraden Ableitungen von f () heben sich heraus. Setzt man die Werte der Integrale
aus Tabellen ein, so erhalt man das Endergebnis
Z
I = Cf
0
f () d + 6 (kB T )2 f 0():::g:
2
(11.16)
Mit (11.16) und (11.6) wird aus (11.4)
2
N = 32 (2V)3 C 3=2 f1 + 8 ( kBT )2 + :::g;
benutzt man
)3 )2=3 ;
T =0 = F = (3N (2
2V C
so wird fur niedrige Temperaturen T 6= 0
2 ( kB T )2:::g:
= F f1 , 12
F
Entsprechend (siehe U B)
2 ( kB T )2:::g:
U = 53 N F f1 + 512
F
110
(11.17)
(11.18)
(11.19)
(11.20)
Wichtig an Gleichung (11.20) ist, da die Korrekturen zu T = 0 mit T 2, und nicht linear
mit T , beginnen. Aus (11.20) folgt namlich direkt das richtige Verhalten von CV fur
niedrige Temperaturen,
CV = const T + :::;
(11.21)
so da CV ! 0 bei T ! 0 in U bereinstimmung mit dem 3. Hauptsatz.
Ein praktisches Beispiel liefert die spezische Warme von Metallen. Tragt man CV =T
gegen T 2 auf, so ndet man bei tiefen Temperaturen ein lineares Verhalten,
CV = a + a T 2 + :::
(11.22)
1
2
T
Der quadratische Term ruhrt von den Gitterschwingungen her (vgl. Kap. 12), wahrend der
a1-Anteil von den (fast frei beweglichen) Leitungselektronen herruhrt. Der experimentelle
Wert von a1 ergibt sich fur viele Metalle in U bereinstimmung mit (11.21). Die spezische
Warme von Metallen bei tiefen Temperaturen zeigt deutlich das Versagen der klassischen
Theorie (wonach die spezische Warme pro Freiheitsgrad 1=2 kB ist, also 3=2 kB fur freie
Elektronen) und gibt eine klare Bestatigung der Quantenstatistik.
Der qualitative Grund fur den geringen Beitrag freier Elektronen zur spezischen
Warme bei tiefen Temperaturen ist klar: Die Einteilchenzustande weit unterhalb der
Fermi-Kante F sind voll besetzt (< n() >= 1) und geben zur inneren Energie (11.5)
einen temperaturunabhangigen Beitrag. Fur die spez. Warme CV tragen also nur die
Elektronen von Zustanden aus der Umgebung der Fermi-Kante bei, also mit abnehmender Temperatur immer weniger Elektronen, da die Fermi-Kante immer scharfer wird.
11.3 Entartung des Fermi-Gases
Der Begri tiefe Temperaturen mu noch prazisiert werden. Dies gelingt anhand von
Formeln wie (11.17), (11.19) oder (11.20), wo kB T=F als Entwicklungsparameter auftritt.
Deniert man durch
kB TF =: F
(11.23)
die Fermi-Temperatur (fur Metalle ist TF 105), die gema (11.18) dichteabhangig ist,
so bedeutet hohe Dichte und niedrige Temperatur, da
T TF
(11.24)
sein mu. In diesem Bereich nennt man ein Fermi-Gas entartet.
11.4 Zustandsgleichung
Fur die grokanonische Gesamtheit ist (vgl. Tabelle (*))
J = J (T; V; ) = U , TS , N
111
(11.25)
das thermodynamische Potential. Benutzt man die fur homogene Systeme gultige Relation
(10.17), so folgt
PV = ,J = kB T ln Zg ;
(11.26)
wenn man noch (7.38) beachtet. Weiter mit (8.11)
PV = kB T
X
i
lnf1 + exp(, (i , ))g
(11.27)
als Zustandsgleichung des idealen Fermi-Gases. Sie enthalt Abweichungen gegenuber der
klassischen Gleichung
(9.124), welche auf das Pauli-Prinzip zuruckzufuhren sind. Die Berechnung von Pi lnf::g in (11.27) lat sich analog Kap.11.2 auf eine Energie-Integration
zuruckfuhren. Das Resultat ist (U B)
2 ( kB T )2::::g;
PV = 52 N F f1 + 512
(11.28)
F
es zeigt, da auch fur T = 0 immer noch PV 6= 0 im Gegensatz zum klassischen idealen
Gas. Der bei T = 0 verbleibende Nullpunktsdruck ist eine direkte Folge des PauliPrinzips, nach dem nur zwei Teilchen mit Spin 1=2 den Impuls h k = 0 annehmen konnen;
alle anderen Teilchen mussen einen hoheren Impuls haben und erzeugen deren Nullpunktsdruck.
11.5 Schwankungen der mittleren Besetzungszahl
Nach Kap. 10.2, Gleichung (10.11), wird
(ni )2 = kB T ( @ <@ni > )
(11.29)
und es folgt mit (11.1)
(ni )2 =< ni > (1, < ni >):
(11.30)
Die Fluktuationen verschwinden fur Energien weit unterhalb der Fermi-Kante, wo <
ni > 1 und weit oberhalb, wo < ni > 0. Mit abnehmender Temperatur konzentrieren
die Fluktuationen sich immer starker in der Nahe der Fermi-Kante.
11.6 Gluhemission
Wir wollen den aus einer (ebenen) Metalloberache austretenden Elektronenstrom berechnen. Dazu nehmen wir an, da die aus dem Metall austretenden Elektronen eine
Potentialdierenz uberwinden mussen.
Das Gleichgewicht zwischen Elektronen im Metall und Elektronen im Vakuum ist dadurch
gekennzeichnet, da die chemischen Potentiale (Index m : Metall, Index v : Vakuum)
gleich sind,
m = v ;
(11.31)
112
Potentialverlauf an der Grenzache zwischen Metall und Vakuum.
fur normale Temperaturen (T 3000K ) konnen wir die Temperaturabhangigkeit von vernachlassigen, so da
m = v = F :
(11.32)
Fur die Teilchendichten erhalten wir
Z 1
1=2
2
m
3=2
d
(11.33)
nv = 4( h2 )
0 expf ( + , F )g + 1
und
Z 1
2
m
1=2
3=2
nm = 4( h2 )
d:
(11.34)
0 expf ( , F )g + 1
Damit das Metall uberhaupt Leitungselektronen halten kann, mu deutlich oberhalb F
liegen, so da wir bei normalen Temperaturen (d.h. F 1)
( , F ) 1
(11.35)
annehmen durfen. Dann kann in nv die 1 im Nenner des Integranden vernachlassigt werden; das Integral der Form
1=2 d = 2 1 x2 dx
(11.36)
0 exp(,x2 )
0 exp()
ist geschlossen losbar und man erhalt fur nv :
nv = 2( 2hm2 )3=2 exp(, (k,TF ) ) (kB T )3=21=2 :
(11.37)
B
Nun kann man die Stromdichte der vom Metall emittierten Gluhelektronen berechnen,
da im Gleichgewicht die Zahl der aus dem Metall austretenden Elektronen gleich der Zahl
der Dampf-Elektronen ist, die auf die Oberache des Metalls auftreen und wieder in die
Metall-Phase ubergehen. Also:
jm = env 21 < jvxj >;
(11.38)
Z
1
Z
113
da die Dichte der Elektronen in der Dampf-Phase gering ist, konnen wir < jvxj > klassisch
berechnen,
s
kB T :
< jvxj >= 2m
(11.39)
Wir erhalten damit als Endergebnis die Richardson-Formel.
jm = e 4hm
(kB T )2 exp(, [k,TF ] ):
(11.40)
3
B
114
Kapitel 12
Das ideale Bose-Gas
12.1 Bose-Verteilung
Die mittlere Besetzungszahl eines Einteilchenniveaus ist fur Bosonen nach (8.13)
< ni >= exp( [ 1, ]) , 1 :
(12.1)
i
Da stets < ni > 0 sein mu, folgt
exp( [i , ]) 1:
(12.2)
Wenn wir also die Skala der Einteilchenenergien so normieren, da der unterste Zustand
o = 0 hat, so mu
0
(12.3)
sein. Den Verlauf von < ni > hatten wir fur hohe Temperaturen (oder geringe Dichte) schon in Kap. 8.4 diskutiert: man erhalt eine exponentiell abfallende BoltzmannVerteilung exp(, [i , ]). Allgemein hat < n() > folgenden Verlauf:
Bose-Verteilung n() fur verschiedene Temperaturen.
Mit abnehmender Temperatur sinkt die Besetzungszahl der energetisch hoheren Zustande
zugunsten der niedrigen. Mit T ! 0 gehen alle Bose-Teilchen in den untersten Zustand
115
0 = 0 uber. Das chemische Potential mu sich dabei so verandern, da die vorgegebene
Teilchenzahl N erhalten bleibt. Fur T ! 0 ruckt immer mehr gegen seinen Grenzwert
0. Wegen der Singularitat von < n() > fur = 0 , T 6= 0, die man aus (12.1) oder
der obigen Skizze abliest, ist die Diskussion tiefer Temperaturen mit Vorsicht anzugehen.
Wir werden ihn in Abschnitt 12.3 diskutieren und dabei auf das Phanomen der BoseEinstein-Kondensation stoen.
12.2 Schwankungen der mittleren Besetzungszahl
Wie in (11.29) bilden wir
mit (12.1) ergibt sich direkt
(ni )2 = ,1( @ <@ni > );
(12.4)
(ni )2 =< ni > (1+ < ni >):
(12.5)
Den Unterschied zum Fermi-Gas, (11.30), sowie zum klassischen Grenzfall, der sich aus
(11.2) zu
(ni )2 =< ni >
(12.6)
ergibt, wird besonders deutlich, wenn man die relative Schwankung betrachtet
(ni)2 = 1 + 1 :
(12.7)
< ni >2
< ni >
Der bemerkenswerte Punkt an (12.7) ist, da fur groe Werte von < ni > die relative
Schwankung nicht wie im klassischen Fall verschwindet, sondern von der Ordnung 1 bleibt!
12.3 Bose-Einstein-Kondensation
Wir kommen nun auf das Verhalten von Bose-Systemen bei tiefen Temperaturen zuruck.
Um die Temperaturabhangigkeit des chemischen Potentials zu untersuchen, greifen wir
auf die Gleichung
X
X
N = < ni >= exp( [ 1, ]) , 1
(12.8)
i
i
i
zuruck, welche bestimmt bei vorgegebenen N und T . Zur Auswertung von (12.8) benutzen wir das gleiche Verfahren wie fur die Fermi-Statistik und die klassische Statistik,
wir ersetzen
Z
X
V
::: ! (2)3 d3k::::
(12.9)
k
Solange nur skalare Groen interessieren, kann die Impuls-Integration durch eine EnergieIntegration ersetzt werden. Wir erhalten so z:B:
N = (2VC)3
1
Z
0
1=2
expf [ , ]g , 1 d
116
(12.10)
mit C aus (11.10). Wenn wir nun bei konstanter Dichte N =V die Temperatur erniedrigen,
mu die (negative) Groe zunehmen, damit der Wert des Integrals in (12.10) konstant
bleibt. Der Grenzwert = 0 deniert dann eine Grenz-Temperatur Tc durch
Z 1
1=2
V
C
N = (2)3 0 expf=(k T )g , 1 d:
(12.11)
c
Um sie zu bestimmen, fuhrt man die dimensionslose Variable z = =(kB Tc) ein,
N = (k T )3=2 C
B c
V
(2)3
z1=2 dz = C 0 T 3=2:
c
0 exp(z ) , 1
Das Integral in (12.12) hat einen endlichen Wert 6= 0, so da
Z
1
2=3
Tc = const ( N
V) :
(12.12)
(12.13)
Auf den ersten Blick ist man versucht, das obige Ergebnis dahin zu interpretieren, da
man ein Bose-Gas nicht bei konstanter Dichte N =V auf Temperaturen T < Tc abkuhlen
kann. Diese U berlegung ist jedoch nicht stichhaltig, da die durch (12.9) gewonnene Formel
(12.10) nur fur T > Tc gultig ist: Der in der ursprunglichen Formel (12.8) divergente Term
mit 0 = = 0 wird in (12.10) durch den Faktor 1=2 unterdruckt.Fur hohe Temperaturen
sind alle Energien so gleichmaig schwach besetzt, da die Unterdruckung des Beitrages
von 0 = 0 bei der Berechnung der Gesamtteilchenzahl N durch (12.10) statthaft ist.
Dagegen halten sich bei niedrigen Temperaturen fast alle Teilchen im Zustand mit 0 = 0
auf, so da dieser Zustand beim U bergang (12.9) separat behandelt werden mu. Also:
1
VC
+
N = exp(,
) , 1 (2)3
1=2
d = N0 + NG
(12.14)
0 exp( [ , ]) , 1
fur T < Tc. Da bei niedrigen Temperaturen T < Tc sehr viele Teilchen im Zustand 0 = 0
sitzen, mu - 0 sein. Dann kann man NG approximieren durch
1=2
1
NG = (2VC)3 0 exp() , 1 d
(12.15)
oder mit z := (12.16)
NG = N ( TT )3=2
Z
1
Z
c
unter Benutzung von (12.12) bzw. (12.13). Dementsprechend wird
N0 = 1 , ( T )3=2 :
N
Tc
Insgesamt ergibt sich folgendes Bild (siehe nachste Seite):
(12.17)
Oberhalb Tc ist die Zahl der Teilchen im Zustand 0 = 0 vernachlassigbar relativ zu
N ; unterhalb Tc steigt N0 rapide an und fur T = 0 ist N0 = N . Diesen Proze der
Ansammlung vieler (schlielich aller) Teilchen im Zustand 0 = 0 bezeichnet man als
117
Die relative Anzahl der Teilchen im Bose-Einstein-Kondensat als Funktion der
Temperatur in Einheiten von Tc.
Bose-Einstein-Kondensation; Tc heit die Kondensations-Temperatur. NG gibt
die Zahl der Teilchen in der Gas-Phase, N0 die des Kondensats an. Bei der Benutzung
des Begries Kondensation mu man sich klar machen, da bei der Bose-EinsteinKondensation die Teilchen im Impuls-Raum getrennt sind, wahrend bei der gewohnlichen
Kondensation (Gas-Flussigkeit) eine Trennung der Phasen im Orts-Raum auftritt.
Ein konkretes Beispiel fur diesen Eekt der Bose-Einstein-Kondensation bietet das 4 HeSystem, welches bei Tc = 2:180K einen deutlichen Phasenubergang zeigt (vgl. 12.4).
Berechnet man Tc aus (12.13), so erhalt man 3:140K . Die U bereinstimmung ist erstaunlich
gut, wenn man bedenkt, da die obige Theorie alle intermolekularen Krafte vernachlassigt!
Anmerkung: Die in (12.14) vorgenommene Aufspaltung von N fordert geradezu die
Frage heraus, ob auer dem Zustand mit 0 = 0 nicht auch noch einige hohere Zustande
mit Energie 1 , 2 ; ::: 6= 0 in gleicher Weise separat behandelt werden mussen. Dies ist
nicht der Fall, wie die folgende U berlegung zeigt. Wir betrachten als typisches Beispiel
den Term
< n1 > = 1
g()
(12.18)
V
V exp( [ , ]) , 1
mit
2 2
2 2
h = 2h 2 V ,2=3
1 = h2mk1 = 2mL
(12.19)
2
2m
(allgemein: i = 2h 2 =(2mV 2=3 )(n2x + n2y + n2z ); V = L3; nx, ny , nz = 0, 1, 2, ..)
und
g(1) = (2s + 1) 3
(12.20)
,
als Entartungsfaktor des 1 -Zustandes. Da e 1, folgt fur V ! 1 (d.h. 1 ! 0)
< n1 > 1
g(1)
1 g(1)
(12.21)
V
V [exp(1) , 1] V 1
,1=3
= 3(2s + 1) 2mV
! 0:
(2h 2 )
118
Fur makroskopische Volumen V genugt es also, den 0 = 0 -Term gesondert zu betrachten.
12.4 Innere Energie und spezische Warme
Bei der Berechnung der inneren Energie U ist zu unterscheiden T > Tc und T < Tc:
Z 1
3=2
V
C
U = (2)3
d fur T > Tc
(12.22)
0 exp( [ , ]) , 1
und
Z 1
3=2
U = exp() , 1 d fur T < Tc:
0
Fur T < Tc konnen wir (wie in Abschnitt 3) dargelegt) , 0 setzen, wahrend fur
T > Tc zu beachten ist, da = (T ) 6= 0 ist. Fur Temperaturen T weit oberhalb Tc
konnen wir die klassische Naherung benutzen mit dem aus Kap. 8.4 schon bekannten
Resultat
U = 23 N kB T:
(12.23)
Fur T < Tc konnen wir die Integration durchfuhren; aus der Substitution z = =kB T ist
sofort abzulesen, da U T 5=2 wird. Das genaue Resultat ist
5=2
U = 0:77N kB T 3=2 ;
(12.24)
Tc
woraus sofort
(12.25)
CV = 1:93N kB ( TT )3=2
c
folgt. U und CV ruhren nur von den Teilchen mit k 6= 0 her. Fur CV erhalt man insgesamt
folgendes Bild:
Spezische Warme CV fur ein Bosonengas als Funktion der Temperatur.
Eine solche Spitze zeigt auch die spezische Warme von 4He bei 2:180K , allerdings in
Form einer Singularitat. Oensichtlich ist das ideale Bose-Gas ein zu einfaches Modell,
um 4He bei tiefen Temperaturen zu beschreiben. Dennoch besteht kein Zweifel, da bei
dem Phasenubergang in 4He bei 2:180K die Bose-Statistik eine wichtige Rolle spielt.
119
12.5 Photonen
Bei Temperaturen T 6= 0 emittiert und absorbiert jeder Korper elektromagnetische Strahlung. In einem evakuierten Hohlraum, dessen Wande auf fester Temperatur T gehalten
werden, wird sich daher ein Gleichgewicht zwischen der Strahlung im Hohlraum und den
Wanden einstellen. Fur einen genugend groen Hohlraum sollte die spezielle Geometrie
keine Rolle spielen. Wir wahlen der Einfachheit halber einen Wurfel mit V = L3 .
Die elektromagnetische Strahlung in einem solchen Hohlraum konnen wir durch ein Photonen-Gas beschreiben. Die Beschreibung des quantisierten elektromagnetischen Feldes durch
Photonen hatten wir in Kap. 4 durchgefuhrt. Die fur die folgenden Betrachtungen wesentlichen Punkte seien noch einmal kurz zusammengestellt:
1. Photonen sind charakterisiert durch ihren Impuls h k, ihre Energie h ! und den Polarisationszustand j . Der Zusammenhang zwischen Energie und Impuls folgt aus der Relativitatstheorie fur Teilchen der Ruhemasse 0,
oder
Die moglichen Werte k sind
E = pc
(12.26)
! = k c:
(12.27)
k = 2L (1; 2; 3); i Z:
(12.28)
2. Photonen haben Spin 1 (da sie einem Vektorfeld zugeordnet sind), sind also Boso-
nen, was sich in den Vertauschungsregeln fur Erzeugungs- und Vernichtungsoperatoren
niederschlagt,
[bj;by j ] = jj ;
(12.29)
alle restlichen Kommutatoren verschwinden.
3. Die Eigenzustande des Strahlungsfeldes sind charakterisiert durch die Angabe der Zahl
der vorhandenen Photonen einer jeden Sorte (; j );
0
0
0
j:::nj ::: > :
0
(12.30)
Eine direkte Photon-Photon-Wechselwirkung (in niedrigster Ordnung) gibt es nicht; Photonen sind unabhangige Teilchen. Die Gesamtenergie E des Strahlungsfeldes setzt sich
also additiv aus den Beitragen der einzelnen Photonen zusammen,
E=
X
;j
h !nj ;
(12.31)
wenn man E relativ zur Energie des Photonen-Vakuums angibt.
Die Hohlraumstrahlung konnen wir nun beschreiben als eine statistische Gesamtheit von
unabhangigen Bosonen (= Photonen), von der wir die Temperatur T und das Volumen
120
V kennen. Im Gegensatz zu einem gewohnlichen Gas kennen wir die Photonenzahl weder
scharf noch im Mittel. Damit hat der statistische Operator die Form
= exp(,Hr );
(12.32)
wobei Hr der Hamiltonoperator des Strahlungsfeldes ist; bei Spurbildung ist zu summieren
uber alle Basiszustande des Fock-Raumes bei festem Volumen. Damit ergibt sich z:B . fur
die mittlere Besetzungszahl der Mode (; j ) :
(12.33)
< nj >= exp( h1! ) , 1 :
Zur Berechnung der mittleren Energie ersetzten wir, da es zwei transversale Polarisationszustande gibt,
1 2
:::: ! (22V)3 4c3
! d!:::::
(12.34)
Z
X
;j
0
Im Gegensatz zu den U berlegungen unter 12.3 bedarf die Stelle ! = 0 (bzw. k = 0) keiner
Sonderbehandlung, da es unsinnig ist, von Photonen mit h ! = 0 und h k = 0 zu sprechen.
Fur die Energie folgt
Z 1
U = V u(!; T ) d!
(12.35)
0
mit der Energiedichte pro Frequenzeinheit
3
(12.36)
u(!; T ) = 2hc3 exp(!h !) , 1 :
Gleichung (12.36) ist das Planck'sche Strahlungsgesetz. Fur h ! kB T wird aus
(12.36)
2
u(!; T ) = kB T !2c3 ;
(12.37)
dies ist das von Rayleigh aus dem Gleichverteilungssatz abgeleitete klassische Gesetz. Es
fuhrt in (12.35) zu der als Ultraviolett-Katastrophe bekannten Divergenz. Im anderen
Extremfall h ! kB T erhalt man das (empirisch gefundene) Gesetz von Wien
3
u(!; T ) = h2!c3 exp(, h !):
(12.38)
Der Verlauf von u(!; T ) gema (12.36) ist unten fur verschiedene Temperaturen skizziert
und spiegelt das Wien'sche Verschiebungsgesetz wider.
Fur die totale Energiedichte schlielich wird
U = (kB T )4 Z 1 x3 dx = 2kB4 T 4:
(12.39)
V 2c3h 3 0 exp(x) , 1
15c3h 3
Gleichung (12.39) wird als Stefan-Boltzmann-Gesetz beteichnet.
Fur die spezische Warme pro Volumeneinheit folgt
CV T 3:
(12.40)
Der Unterschied zu (12.25) erklart sich dadurch, da verschiedene Energie-Impuls-Beziehungen vorliegen: = pc, fur Photonen aber = p2=(2m) fur nichtrelativistische Teilchen
der Masse m.
121
Wien'sches Verschiebungsgesetz
12.6 Detailed Balance
Wir wollen die Prozesse, die zu dem oben vorausgesetzten Gleichgewicht der Hohlraumstrahlung und seiner Umgebung fuhren, etwas genauer untersuchen. Dabei genugt es, die
Emission und Absorption von Photonen einer bestimmten Frequenz ! zu untersuchen.
Sie entspricht (vgl. Kap. 4.5) der Dierenz zweier Energien der Atome der den Hohlraum
begrenzenden Wande:
h ! = E2 , E1 :
(12.41)
Die Zahl der Absorptionsprozesse pro Zeiteinheit ist
d12 = B N u(!; T );
(12.42)
12 1
dt
wo N1 die Zahl der Atome im Zustand 1, u(!; T ) die Energiedichte der Photonen der
Frequenz !, und B12 die Wahrscheinlichkeit fur den elementaren Proze der Absorption
ist.
Fur die Zahl der Emissionsprozesse ist zu berucksichtigen, da es neben der induzierten
Emission (Umkehrung der durch B12 beschriebenen induzierten Absorption) noch die
spontane Emission (vgl. Kap. 4.5) gibt. Also:
d21 = B N u(!; T ) + A N ;
(12.43)
21 2
21 2
dt
wo B21 und N2 entsprechend zu (12.42) erklart sind und A21 die Wahrscheinlichkeit
des elementaren Prozesses der spontanen Emission ist. Solange der Hamilton-Operator
zeitumkehr-invariant ist, folgt aus der Mikro-Reversibilitat
B12 = B21 :
(12.44)
Diese generell als Detailed Balance bezeichnete Aussage folgt auch direkt aus (4.37)
und den folgenden Gleichungen. Im thermischen Gleichgewicht mu nun gelten
d12 = d21
dt
dt
122
(12.45)
oder
Weiter ist
B12 N1u(!; T ) = B12 N2u(!; T ) + A21 N2 :
(12.46)
N1 = exp(,E1 ) = exp(, (E , E )) = exp( h !);
(12.47)
1
2
N2 exp(,E2 )
da die Atome bei der Temperatur T durch den statistischen Operator exp(, H0) beschrieben werden; H0 sei der Hamilton-Operator der Atome. Man gelangt so zu
1
A21
(12.48)
u(!; T ) = B
!) , 1 :
21 exp( h
Benutzt man das fur hohe Frequenzen gultige Wien'sche Gesetz aus (12.38), so erhalt
man fur A21 =B21
A21 = h !3
(12.49)
B21 2 c3
und (12.48) geht in das Planck'sche Gesetz (12.36) uber.
Auf den ersten Blick scheint es so, als habe man das Planck'sche Strahlungsgesetz hergeleitet, ohne das Konzept der Photonen zu benutzen, d:h. im Rahmen der klassischen
Strahlungstheorie. Der scheinbare Widerspruch lost sich, wenn man sich erinnert, da die
oben benutzte spontane Emission direkte Konsequenz der Quantisierung des Strahlungsfeldes ist (Kap. 4.5).
Gleichung (12.48) zeigt, da das Planck'sche Gesetz materialunabhangig gilt. Die separaten U bergangswahrscheinlichkeiten A21 und B21 = B12 hangen uber (4.45) und (4.46)
von der Atomsorte ab; der Quotient A21 =B21 jedoch wird unabhangig von der Atomsorte.
12.7 Phononen in Festkorpern
Die Gitterbausteine eines Festkorpers konnen um ihre Gleichgewichtslagen Schwingungen
ausfuhren. Bei nicht zu hohen Temperaturen sind die Schwingungen klein, soda anharmonische Eekte vernachlassigt werden konnen. Die Hamilton-Funktion des Kristalls ist
dann eine quadratische Form,
N
N
2
X
X
Hkl: = 2pm + 21
K q q :
(12.50)
=1
; =1
Darin sind p , q die Impulse und Auslenkungen der Teilchen, m ihre Massen, und K
die Kraftkonstanten. Durch eine lineare Transformation der p , q ist es stets moglich,
die Schwingungen zu entkoppeln. Man erhalt dann 3N Normal-Schwingungen mit Frequenzen !i (Genau genommen 3N-6 nach Abzug der Freiheitsgrade der Translation und
Rotation; fur makroskopische Systeme ist diese Korrektur vernachlassigbar). Die Quantisierung eines solchen Systems entkoppelter harmonischer Oszillatoren gelingt, wie in Kap.
4.2 fur das elektromagnetische Feld vorgefuhrt. Die moglichen Energien des Kristalls bei
Schwingungsanregungen sind dann gegeben durch
N
X
E = E0 + h !i(ni + 21 ):
(12.51)
i=1
123
Die Schwingungsquanten nennt man Phononen; sie sind charakterisiert durch ihre Energie h !i, den Ausbreitungsvektor ki, der mit !i durch eine Dispersionsrelation verknupft
ist, und ihre Polarisation, entsprechend longitudinalen und transversalen Schwingungen.
In der harmonischen Naherung sind die Phononen unabhangige Teilchen, die der BoseStatistik gehorchen.
Wir betrachten nun einen Kristall mit Volumen V und Temperatur T . Wie beim Photonengas kennen wir die Gesamtzahl der Phononen nicht (Nicht zu verwechseln mit der
Zahl der Gitterbausteine N ; sie bestimmt die Zahl der moglichen Frequenzen !i!). Also
konnen wir sofort angeben
(12.52)
< ni >= exp( h1! ) , 1
i
fur die mittlere Anzahl von Phononen vom Typ i bei gegebener Temperatur kB T = 1=
und gegebenem Volumen V , welches in die Bestimmung der !i eingeht. Als charakteristische Eigenschaft wollen wir die spezische Warme des Kristalls berechnen. Dazu
benotigen wir
X
X
U = h !i < ni >= exp(hh!!i ) , 1 :
(12.53)
i
i
i
Die Berechnung der Frequenzen !i = !i(ki) ist ein kompliziertes Problem, welches von
der atomaren Struktur des Kristalls abhangt. Die Ergebnisse einer solchen Rechnung sind
nicht in Form einfacher Funktionen ! = !(k) angebbar. Wir betrachten daher ein Modell,
welches einfach genug ist, um Ausdrucke wie (12.53) ausrechnen zu konnen, und doch
hinreichend realistisch bleibt. In diesem Debye-Modell macht man zwei Naherungen:
1.) Da fur makroskopische Korper die !i dicht beieinander liegen, ersetzt man die Summanden durch eine Integration
Z
X
X
::: = (2s + 1) ::: = (2s + 1) (2V)3 d3k::::
(12.54)
i
k
Dabei ist die Integration so zu begrenzen, da die Zahl der Freiheitsgrade 3N erhalten
bleibt.
2.) Als Zusammenhang von ! und k nimmt man eine simple Dispersionsrelation an
! = c0k;
(12.55)
mit c0 als Ausbreitungsgeschwindigkeit der Schwingungen im Kristall. Diese Naherung
entspricht (12.27) fur Photonen und ist geeignet, langwellige akustische Schwingungen in
einem isotropen Medium zu beschreiben; c0 ist die gewohnliche Schallgeschwindigkeit.
Die fur kleine k-Werte gultige Relation (12.55) benutzt man im Debeye-Modell fur alle
Frequenzen bis zur Maximal-Frequenz !m, gegeben durch (2s + 1 = 3) :
Z k
X
m 2
3
V
= (2)3 4
k dk = (2V2) km3 = 3 N;
(12.56)
0
i
also
2
(12.57)
km = ( 3 NV 2 )1=3
124
oder
Damit wird
oder
1=3
!m = c0(62 N
V) :
U = (23V2c3)
0
!m
Z
0
!2 exp(hh!!) , 1 d!
(12.58)
(12.59)
U = 9(kB T )4 h!m
t3 dt:
(12.60)
N (h!m )3 0
exp(t) , 1
Deniert man die Debeye-Funktion durch
3
x
t
1
(12.61)
D(x) = x3 (exp(t) , 1) dt;
0
so wird
U = 9 k T D ( TD )
(12.62)
B
N
T
mit der durch
kB TD =: h !m
(12.63)
denierten Debeye-Temperatur TD . Fur die Grenzfalle T ! 0, T ! 1 lassen sich die
expliziten Werte von D(TD =T ) leicht angeben, und man erhalt
U = 3 k T fur T T ;
(12.64)
B
D
N
U = 3 4k T ( T )3 fur T T :
(12.65)
D
N
5 B T
Z
Z
D
Daraus folgt fur die spezische Warme pro Gitterbaustein
CV = 3 kB fur T TD
(12.66)
T 3 fur T T :
4
CV = 12
k
(12.67)
B( )
D
5
TD
Dabei ist in der Praxis TD 102. Bei niedrigen Temperaturen verschwindet CV mit T 3
in U bereinstimmung mit dem 3. Hauptsatz und dem experimentellen Befund.
Bei hohen Temperaturen wird das klassische Resultat (Regel von Dulong-Petit) mit
CV = 3kB bestatigt.
Das Debye-Modell hat sich bei einatomigen Kristallen bewahrt, wenn man sehr hohe
Temperaturen (in der Nahe des Schmelzpunktes) ausschliet, wo die harmonische Naherung versagt. | Schwache Anharmonizitaten kann man mit Hilfe der thermodynamischen
Storungsrechnung (Kap. 10.3) behandeln. | In mehratomigen Gittern versagt das einfache Modell, da dort zusatzlich optische Schwingungen auftreten. Beispiel: Schwingungen
der Na+-Ionen gegen die Cl, Ionen im Na Cl-Kristall.
125
Spezische Warme CV als Funktion der Temperatur fur einatomige Kristalle.
126
Kapitel 13
Magnetische und elektrische
Eigenschaften der Materie
Bringt man Materie in ein magnetisches (elektrisches) Feld, so entsteht eine makroskopische Magnetisierung (Polarisation). Dabei spielen die beiden folgenden Eekte eine gegenlauge Rolle:
1. Schon vorhandene Dipolmomente (permanente Dipolmomente) werden im aueren Feld
ausgerichtet. Dies fuhrt zum temperaturabhangigen Paramagnetismus bzw. dem entsprechenden elektrischen Analogon, der Orientierungspolarisation.
2. A uere Felder konnen Diplomomente induzieren: Ein elektrisches Feld kann die Schwerpunkte positiver und negativer Ladungen in Atomen und Molekulen gegeneinander verschieben und so elektrische Dipole erzeugen (oder verandern). Magnetische Felder andern
die Elektronenzustande, insbesondere den Bahndrehungsimpuls; damit verknupft ist eine
A nderung der atomaren magnetischen Momente: Diamagnetismus.
In der Praxis treten beide Phanomene simultan auf; die Aussage, eine Substanz sei paramagnetisch, besagt also, da der Paramagnetismus den Diamagnetismus uberdeckt.
Das an einem atomaren Moment angreifende Feld setzt sich zusammen aus dem aueren
Feld umd dem von den atomaren Momenten der Umgebung erzeugten Feld. Wir
werden im folgenden den zweiten Anteil vernachlassigen; dies ist z:B . fur die Behandlung
des Paramagnetismus von Gasen legitim im Gegensatz zum Ferromagnetismus, wo
gerade der zweite Anteil essentiell ist.
Wir wollen im folgenden einige einfache Falle untersuchen und dabei zeitlich und raumlich
konstante Felder voraussetzen.
13.1 Denitionen
Als Betrag der Magnetisierung M denieren wir (die Feldstarke B ist hier als klassische
Groe gemeint)
M = jM~ j = , < @H
(13.1)
@B >;
127
wo B der Betrag des Magnetfeldes ist und H der Hamilton-Operator des Systems bei
Anwesenheit des aueren Feldes. Eine solche Denition ist plausibel, da ,~ B die Energie
eines magnetischen Moments ~ im Feld B darstellt.
Entsprechend hat man
@H >
(13.2)
P =: , < @E
l
fur den Betrag der Polarisation; El ist dabei der Betrag des elektrischen Feldes El.
13.2 Theorem von Bohr - van Leeuwen
Im Rahmen einer streng klassischen Theorie ist die Magnetisierung stets null.
Der Beweis fur dieses Theorem ist auerst einfach: Da es in der klassischen Physik keinen
Spin gibt, ist das Magnetfeld in Hkl: nur in der Form
X 1
e
2
(
p
(13.3)
i , A(ri ; t))
2
m
c
i
i
vertreten. Die mit Hkl: gebildete Zustandssumme Zg;kl: (vgl. Kap. 5.4) ist aber gegen die
Transformation
pi ! pi , ec A(ri)
(13.4)
invariant, da die klassische Verteilungsfunktion kl: fur die harmonische Gesamtheit auch
nur uber Hkl: vom Magnetfeld abhangt und das Volumenelement in (5.37) sich unter (13.4)
nicht andert. Magnetismus ist also ein typisch quantenmechanisches Phanomen.
13.3 Paramagnetismus
Um den Paramagnetismus in Reinkultur untersuchen zu konnen, betrachten wir ein System von N lokalisierten magnetischen Momenten in einem aueren Feld
B = (0; 0; B ):
(13.5)
Dabei ruhren die magnetischen Momente vom Spin der betrachteten Teilchen her, z:B .
von Atomen oder Atomkernen mit Gesamtdrehimpuls J 6= 0:
Der Hamilton-Operator eines solchen Systems hat dann die einfache Form (Wechselwirkungen zwischen den einzelnen Spins seien vernachlassigt):
mit
H = ,B g J B = ,B g B Jz
(13.6)
h ;
B = 2emc
(13.7)
128
wo m die Elektronen- oder Nukleonenmasse ist, g der gyromagnetische Faktor (= 2 fur
Elektronen-Spins) und
N
X
J = ji
(13.8)
i=1
der Gesamtdrehimpuls des Systems (in Einheiten von h ). Die moglichen Energien des
Systems sind
EmJ = ,B g M mJ
(13.9)
bei
mJ = ,J; ,J + 1; :::::; +J:
(13.10)
Bei gegebener Temperatur T ist der statistische Operator
,H )
(13.11)
= Spexp(
(exp(,H ))
und es wird, da < H > sich additiv aus den Beitragen der einzelnen Momente zusammensetzt:
X
Km)
< H >= ,K N m Pexp(
(13.12)
m exp(Km)
m
mit der Abkurzung
K =: B g B;
(13.13)
und
m = ,j; ,j + 1; ::::; +j
(13.14)
wenn j der Spin der einzelnen Teilchen ist. Aus (13.12) folgt mit (13.1)
X
Km) ;
M = B g N m Pexp(
(13.15)
m exp(Km)
m
also gerade der Mittelwert des Operators
Mz = B g Jz
wie zu erwarten.
Die Summation in (13.15) kann direkt ausgefuhrt werden. Mit der Abkurzung
=: K = kB gTB
B
wird zunachst (geometrische Reihe!)
X
exp(m) = [exp(,j ) , expf(j + 1)g]
1 , exp()
m
oder symmetrischer
X
j + 1=2)] :
exp(m) = sinh[(
sinh(1=2)
m
129
(13.16)
(13.17)
(13.18)
(13.19)
Schreibt man die Zustandssumme als
X
Zg = ( exp(m))N ;
m
(13.20)
so wird
ln Zg = N fln[sinh((j + 1=2))] , ln[sinh(1=2)]g:
(13.21)
Daraus erhalt man mit
(13.22)
M = kB T @ ln@BZg
schlielich durch Dierentiation von (13.21)
M = N B g j Bj ();
(13.23)
wenn man die Brillouin-Funktion
Bj =: 1j f(j + 21 ) coth([j + 12 ]) , 12 coth( 12 )g
(13.24)
einfuhrt.
Wir diskutieren fur das Verstandnis des Verlaufs von Bj () die Grenzfalle 1 und
1:
1. 1 : Starke Felder/niedrige Temperaturen; da
coth(x) ! 1 fur x ! 1
(13.25)
wird
Bj () ! 1j f(j + 12 ) , 21 g = 1
(13.26)
fur ! 1. Entsprechend wird
M = N B g j:
(13.27)
Alle elementaren Momente sind in Feldrichtung ausgerichtet; M nimmt seinen Maximalwert an.
2. 1 : Schwache Felder/hohe Temperaturen. Benutzt man
coth(x) x1 + 13 x fur x 1;
(13.28)
so wird
(13.29)
Bj () (j +3 1) ;
also
M =B
(13.30)
mit der magnetischen Suszeptibilitat
2 2
= N g B3kj (jT+ 1) = T :
(13.31)
B
Gleichung (13.31) ist das Curie'sche Gesetz.
130
13.4 Klassische Theorie des Paramagnetismus und
der Orientierungspolarisation
Permanente magnetische Momente konnen klassisch jede beliebige Orientierung zu einem aueren Magnetfeld einnehmen. Der Mittelwert des magnetischen Moments einer
Substanz kann daher durch Mittelung uber alle moglichen Richtungen berechnet werden,
Mkl: =
,1 dR(cos #)0 cos # exp(0B cos #) :
1
,1 d(cos #) exp(0B cos #)
R1
(13.32)
Dabei ist # der Winkel zwischen B und ; ,~ B = ,0 B cos # ist die Energie des
Moments im Magnetfeld B; jedes Moment liefert im Mittel den gleichen Beitrag, daher
der Faktor N . Die Integrale in (13.32) sind elementar losbar, das Resultat ist (U B):
(13.33)
Mkl: = N0fcoth(0B ) , 1 B g:
0
Zum gleichen Ergebnis gelangt man, wenn man in (13.23) bei der Identikation
0 B g j
(13.34)
den Grenzfall j ! 1 untersucht. Dies ist plausibel, da mit wachsendem j die Zahl der magnetischen Zustande zunimmt, von denen jeder einer bestimmten klassischen Orientierung
entspricht.
Entsprechend (13.32) kann man die Polarisation eines Dielektrikums berechnen. Fur den
Mittelwert des elektrischen Dipolmoments P im Feld El erhalt man
Pkl: = N P0 fcoth(P0El ) , P1 E g:
(13.35)
0 l
Dabei ist P0 der Betrag des elementaren Dipolmoments.
13.5 Magnetische Kuhlung
Aus (13.21) lat sich uber (7.30) die Entropie des betrachteten Spin-Systems berechnen.
Das Resultat ist in der Skizze qualitativ dargestellt:
Die wesentlichen Punkte sind auch ohne Rechnung klar: nach dem 3. Hauptsatz gilt S ! 0
fur T ! 0 unabhangig davon, welche Werte andere Parameter annehmen, von denen S
abhangt, z:B . das Magnetfeld B; nach unserer statistischen Einfuhrung der Entropie ist
klar, da bei sonst gleichen Parametern S mit wachsender Feldstarke B abnimmt.
An dem Diagramm (obige Skizze) kann man das Prinzip des Verfahrens zur Erzeugung tiefer Temperaturen durch adiabatische Entmagnetisierung ablesen: Man schaltet
zunachst ein Magnetfeld isotherm ein; durch adiabatisches Ausschalten (S =const.) erreicht man dann eine Temperaturerniedrigung, die umso groer ist, je groer das Magnetfeld war. Wie in Kap. 9.9 sieht man, da der absolute Nullpunkt mit endlich vielen
solchen Schritten nicht zu erreichen ist.
131
Beispiel fur die magnetische Kuhlung.
13.6 Negative Temperaturen
Normalerweise erwartet man, da die Entropie eines Systems mit wachsender Energie
monoton zunimmt, da die Zahl der Realisierungsmoglichkeiten eines Makrozustands mit
der Energie gewohnlich wachst. Aus
1 = ( @S )
(13.36)
T @U V;N
folgt dann, da T positiv ist.
Nun gibt es aber Systeme (wie die in 13.3 besprochenen Spin-Systeme), deren Energie
nicht nur eine untere, sondern auch eine obere Grenze besitzt. Fur Teilchen mit Spin
1=2 ist z:B . 1=2 NK die obere, ,1=2 NK die untere Grenze. Beide Zustande haben die
gleiche Zahl von Realisierungsmoglichkeiten (namlich genau 1 -alle Spins parallel bzw.
antiparallel zum Magnetfeld- ); also kommt beiden Zustanden die gleiche Entropie zu, da
die gleiche Information vorliegt. Man erhalt daher qualitativ die folgende Kurve:
Fur U < 0 ist die Ableitung von S und damit von T positiv, dagegen fur U > 0 negativ.
Zur Parametrisierung der obigen Kurve ware es sinnvoll, nicht T , sondern = ,1=T
einzufuhren; mit U wachst dann auch :
Zustande negativer Temperatur konnen experimentell bei Kernmomenten in Kristallen
realisiert werden, vorausgesetzt, da die Spin-Gitter-Wechselwirkung schwach ist gegenuber
der Spin-Spin-Wechselwirkung (die in 13.3) nicht erfat war), welche die Einstellung des
thermischen Gleichgewichts im Spin-System besorgt. Man magnetisiert die Kernspins dabei zunachst in einem starken Magnetfeld und dreht dessen Richtung dann so schnell um,
da die Spins nicht folgen konnen. Dadurch entsteht aus der ursprunglichen Verteilung
n expf,En =kB T g eine neue mit einer Besetzungsinversion 0n expfEn=kB T g =
132
Entropieverlauf S als Funktion der inneren Energie U fur ein Spinsystem in aueren
Magnetfeld.
expf,En=(,kB T )g. Zustande mit Besetzungsinversion spielen in der Maser- und LaserPhysik eine wichtige Rolle.
133
Teil IV
Nichtgleichgewichts - Dynamik
134
Kapitel 14
Kinetische Theorien fur Fermionen
Wahrend wir bisher physikalische Systeme von Fermionen, Bosonen oder klassischen Teilchen im thermodynamischen Gleichgewicht betrachtet haben, bzw. deren Response unter kleinen aueren Storungen (Kap. 10), bleibt weiterhin ungeklart, wie diese Systeme
den endgultigen Gleichgewichtszustand erreichen. Dazu ist die Formulierung einer konsistenten Nichtgleichgewichts - Dynamik erforderlich, die die explizite Zeitentwicklung
des physikalischen Systems beschreibt. Einerseits kann man dafur auf die zeitabhangige
Schrodingergleichung (2.3) zuruckgreifen und mit Hilfe Green'scher Funktionen ein System kinetischer Gleichungen ableiten, andererseits kann auch die Zeitentwicklung der
N -Teilchen Dichtematrix in geeigneten Naherungen direkt betrachtet werden.
14.1 Der Dichtematrix - Formalismus
Ausgangspunkt einer entsprechenden Theorie ist die von-Neumann Gleichung (5.4) fur
den Dichteoperator N , der ein N -Teilchen Fermionensystem in einem reinen oder
gemischten Zustand beschreibt,
@ (1; ::; N ; 10::N 0 ; t) = [H ; ];
ih @t
(14.1)
N
N N
wobei HN den N -Teilchen Hamiltonoperator darstellt, und wir zur Abkurzung i i fur
den Variablensatz von Teilchen i benutzt haben (z:B : i ri; i ; i Ortskoordinate,
Spin, Ispspin etc.). Falls das System von Fermionen nur uber eine Zwei-Teilchen Wechselwirkung v(ij ) zwischen Teilchen i und j wechselwirkt, was naherungsweise fur die meisten
physikalischen Falle zutrit, so lautet der Hamiltonoperator explizit
HN =
wobei
N
X
i=1
h (i) +
0
NX
,1
i<j
v(ij );
(14.2)
h0(i) = t(i) + U 0 (i)
(14.3)
den Einteilchenanteil von HN , bestehend aus dem Operator der kinetischen Energie des
Teilchens i und einem aueren mittleren Feld U 0 (i), darstellt. Gleichung (14.1) ist allerdings in der obigen Form fur ein Vielteilchensystem praktisch nicht losbar, so da man
auf Naherungslosungen angewiesen ist.
135
Zu diesem Zweck fuhren wir reduzierte Dichtematrizen n (1:::n; 10:::n0 ; t) ein, die uber
Spurbildung der Teilchen n + 1; ::; N aus der N -Teilchendichte N deniert sind:
n = (N ,1 n)! Spn+1;:::;N N = n +1 1 Spn+1fn+1g:
(14.4)
Wahrend die relative Normierung zwischen n und n+1 festliegt, konnen wir die absolute
Normierung von N frei wahlen. Zweckmaigerweise wahlt man nicht die Normierung
auf 1 { wie in den vorhergehenden Kapiteln { sondern auf N !, so da die Spur uber die
Einteilchen-Dichtematrix
X
Sp1=1 (110; t) = < ayi ai >= N
(14.5)
0
i
ergibt, wobei ayi und ai die Fermionen Erzeugungs- und Vernichtungsoperatoren mit den
bekannten Vertauschungsrelationen (2.44) - (2.46) darstellen. Fur die Zweiteilchen- Dichtematrix folgt dann die Normierung
X
X
X
Sp(1;2) 2 = < ayi ayj aj ai >= , < ayi ayj ai aj >= f< ayi aiayj aj > , < ayi aj > ij g
i;j
i;j
i;j
(14.6)
X
y
= (N , 1) < aj aj >= N (N , 1):
j
Analog ergeben sich die Spuren der Dichtematrizen n (fur n N ) zu (U B)
Sp(1;::;n)n = (N N,! n)! ;
(14.7)
da fur n = N die Dichtematrix N nach (14.7) auf N ! normiert ist.
Wendet man die partielle Spurbildung (d.h. Sp(n+1;::;N )) auf die von-Neumann Gleichung
(14.1) an, so erhalt man ein gekoppeltes System von Dierentialgleichungen 1. Ordnung
in der Zeit, das als BBGKY-Hierarchie (nach den Autoren Bogolyubov, Born, Green,
Kirkwood und Yvon) benannt ist,
@ = [ N h0 (i); ] + [ n,1 v(ij ); ] +
ih @t
n
n
n
N
X
X
X
i=1
1=i<j
i=1
Spn+1[v(i; n + 1); n+1]
(14.8)
fur 1 n N mit N +1 = 0. Explizit lauten die Gleichungen fur n = 1 und 2, die wir im
folgenden lediglich benotigen:
@ = [h0(1); ] + Sp [v(12); ];
ih @t
(14.9)
1
1
2
2
2
@ = [X
ih @t
h0(i); 2 ] + [v(12); 2] + Sp3[v(13) + v(23); 3];
(14.10)
2
i=1
die fur sich noch nicht geschlossen sind, da die Zeitentwicklung von 2 noch durch die
3-Teilchen Dichtematrix 3 bestimmt wird. Um ein geschlossenes Gleichungssystem zu
erhalten, mu daher eine Naherung fur 3 durchgefuhrt werden.
136
14.2 Separation von Korrelationsfunktionen
Da bei unabhangigen Teilchen (ohne Restwechselwirkung) N -Teilchenzustande als antisymmetrische Produkte von Einteilchenwellenfunktionen (Slater-Determinanten, siehe
(2.13)) geschrieben
werden konnen, womit N zu einer Bilinearform von Slater- DeterP
minanten N = i;j pij ji >< j j wird, stellt man zunachst die reduzierten Dichtematrizen n als antisymmetrisierte Produkte von Einteilchen-Dichtematrizen dar und
fuhrt fur wechselwirkende Teilchen Korrekturen in Form von Korrelations-Funktionen
oder -Matrizen ein. Dieses Verfahren ist in der Literatur als Cluster-Entwicklung bekannt. Von Interesse ist im gegenwartigen Zusammenhang lediglich die explizite ClusterEntwicklung bis zur 3. Ordnung, die wie folgt eingefuhrt wird,
1 (110) = (110);
(14.11)
2 (12; 1020) = (110)(220) , (120)(210) + c2 (12; 1020)
(14.12)
= 20 (12; 1020) + c2 (12; 1020) = A12(110 )(220) + c2(12; 1020);
mit dem 2-Teilchen Antisymmetrisierungsoperator Aij = 1,Pij , wahrend die Entwicklung
von 3 neben den dreifachen Produkten von noch die symmetrisierten Produkte (bzgl.
der Indexpaare (ii0)) und antisymmetrischen Produkte (bzgl. der Permutationen Pij oder
Pi j ) von c2 enthalt,
0
0
3 (123; 102030) = (110)(220)(330) , (120)(210)(330)
(14.13)
,(130)(220)(310) , (110)(320)(230)
+(130)(210)(320) + (120)(310 )(230)
+(110)c2(23; 2030 ) , (120)c2 (23; 1030)
,(130)c2 (23; 2010) + (220)c2 (13; 1030)
,(210 )c2(13; 2030) , (230)c2(13; 1020)
+(330)c2(12; 1020 ) , (310)c2 (12; 3020)
,(320 )c2(12; 1030) + c3(123; 102030):
Vernachlassigt man in (14.12) die 2-Teilchen Korrelationsfunktion c2 und in (14.13) sowohl
c2 als auch c3 , so erhalt man gerade den bekannten Limes unabhangiger Teilchen; dies
besagt andererseits, da alle Eekte der Restwechselwirkung durch c2 beschrieben werden.
Die 2-Teilchen Korrelationsfunktion c2 besitzt die gleichen Symmetrien unter Teilchenaustausch wie die hermitesche 2-Teilchen Dichtematrix 2 , d:h:
c2(12; 1020) = ,c2 (12; 2010) = ,c2 (21; 1020) = c2 (1020; 12) u:s:w:
(14.14)
Der entscheidende Schritt in den hier benotigten Cluster-Entwicklungen ist nun die Vernachlassigung der 3-Teilchen Korrelationsfunktion c3 in (14.13), da bei moderaten Restwechselwirkungen die 3-Teilchen Dichtematrix 3 recht gut durch die verbleibenden Terme
in (14.13) dargestellt wird. Mit der Naherung c3 = 0 wird das Gleichungssystem (14.9)
137
und (14:10) geschlossen und wir erhalten durch Einsetzen von (14.12) und (14.13) in (14.9)
und (14.10) die ersten Gleichungen der Korrelationsdynamik fur die Zeitentwicklung
von (110; t)
@ (110 ; t) = [h0(1) , h0(10)](110; t)
ih @t
(14.15)
+Sp(2 = 20)[v(12)A12 , v(1020)A1 2 ](110; t)(220; t) + Sp2=2 [v(12) , v(1020 )]c2(12; 1020; t)
sowie (nach etwas langerer Rechnung) fur die Zeitentwicklung von c2 ,
0
0
0
@ c (12; 1020; t) = [h0(1) + h0 (2) , h0 (10) , h0(20)]c (12; 1020; t)
ih @t
2
2
(14.16)
+Sp(3=3 )[v(13)A13 + v(23)A23 , v(1030)A1 3 , v(2030)A2 3 ](330 ; t)c2(12; 1020; t)
+[v(12) , v(1020)]20 (12; 1020)
,Sp(3=3 ) fv(13)(230; t)20(13; 1020; t) , v(1030)(320; t)20 (12; 1030; t)
+v(23)(130; t)20 (32; 1020; t) , v(2030)(310; t)20 (12; 3020; t)g
0
0
0
0
0
0
+[v(12) , v(1020)]c2(12; 1020; t)
,Sp(3=3 )fv(13)(230; t)c2(13; 1020; t) , v(1030)(320; t)c2 (12; 1030; t)
+v(23)(130; t)c2(32; 1020; t) , v(2030)(310; t)c2(12; 3020; t)g
0
+Sp(3=3 ) f[v(13)A13A1 2 , v(1030)A1 3 A12](110; t)c2(32; 3020; t)
+[v(23)A23A1 2 , v(2030)A2 3 A12 ](220; t)c2(13; 1030; t)g:
0
0
0
0
0
0
0
0
0
Die obigen Gleichungen (14.15) und (14.16) sind bisher nur fur spezielle Probleme numerisch gelost worden, so da eine explizite Diskussion uber den Rahmen der Vorlesung
hinausgeht. Zur Kompaktizierung und Verdeutlichung der physikalischen Terme fuhrt
man zweckmaigerweise den Einteilchen-Hamiltonoperator
h(i) = h0 (i) + U s (i) = h0(i) + Sp(n=n )v(in)Ain(nn0 ; t);
0
(14.17)
h(i0 ) = h0(i0 ) + U s(i0 ) = h0 (i0) + Sp(n=n ) v(i0n0 )Ai n (nn0 ; t)
0
0
0
ein, der nicht nur die Wechselwirkung mit dem aueren Feld U 0 enthalt, sondern auch
die mittlere Selbstwechselwirkung U s(i) der Teilchen untereinander. Weiterhin fuhrt man
den Pauli-Blocking Operator
Q=ij = 1 , Sp(n=n ) (Pin + Pjn)(nn0 ; t); Q=i j = 1 , Sp(n=n ) (Pi n + Pj n )(nn0 ; t); (14.18)
0
0
0
0
0
0
0
0
sowie die eektive Wechselwirkung im Medium V =(ij ) ein uber
V =(ij ) = Q=ij v(ij ); V =(i0j 0) = Q=(i0j 0 )v(i0j 0);
138
(14.19)
wobei die Austauschoperatoren in Q= (14.18) auf alle Terme nach rechts wirken.
Die Gleichungen fur und c2 lassen sich dann in der kompakteren Form schreiben,
@ (110; t) = [h(1) , h(10)](110; t) + Sp [v(12) , v(1020)]c (12; 1020 ; t); (14.20)
ih @t
(2=2 )
2
und
2
2
X
@ c (12; 1020; t) = [X
h
(
i
)
,
h(i0)]c2 (12; 1020; t)
(14.21)
ih @t
2
0
0
i=1
i =1
0
0
0 0
+[V (12) , V
20 (12; 1 2 ; t)
+[V =(12) , V =(1020)]c2(12; 1020 ; t)
+Sp(3=3 ) f[v(13)A13A1 2 , v(1030)A1 3 A12](110; t)c2(32; 3020; t)
+[v(23)A23A1 2 , v(2030)A2 3 A12 ](220; t)c2(13; 1030; t)g:
=
=
0
0
0
(1020)]
0
0
0
0
0
0
Gleichung (14.20) beschreibt die Propagation eines Teilchens im mittleren Feld U 0 (i) +
U s(i) unter Einbeziehung der Zweiteilchendynamik, die in (14.21) naher speziziert wird.
Wahrend in (14.21) die Terme mit h(i) nun die Propagation von 2 Teilchen im mittleren Feld beschreiben, lassen sich die Terme mit V = auf 2-Teilchenstoe im Medium
zuruckfuhren (kurzreichweitige Korrelationen). Die Wechselwirkungsterme in den letzten
beiden Zeilen sind vorwiegend fur die langreichweitigen Korrelationen des N -Teilchensystems zustandig.
14.3 Entwicklung in einer Einteilchenbasis
Die Ortsraumdarstellung der gekoppelten Gleichungen fur und c2 (14.20) und (14.21) ist
in der gegenwartigen Form fur eine numerische Integration sowie fur weitere analytische
Naherungen nicht besonders geeignet. Daher entwickeln wir und c2 nach einer zunachst
beliebigen Einteilchenbasis ' j >;
(110; t) =
c2(12; 1020; t) =
0
(t)'(r)' (r0);
0
0
(14.22)
0
C (t)' (r1)' (r2)' (r01)' (r02);
X
X
0
0
0
0
0
(14.23)
und setzen diese Entwicklungen in (14.20) und (14.21) ein. Durch Multiplikation von
links mit '(r1)' (r1 ) bzw. ' (r1)' (r2)' (r1 )' (r2 ) fur (14.21) und Integration uber
d3r1d3r1 bzw. d3r1d3 r2d3r1 d3r2 erhalten wir die Gleichungen fur die Zeitentwicklung der
Koezienten (t),
@ = X[h , h ]
ih @t
(14.24)
X
+ f< jvj > C , C < jvj0 >g
0
0
0
0
0
0
0
0
0
0
0
0
bzw. C (t)
0
0
0
139
0
@ C
ih @t
=
0
fhC + hC , h C , h C g
X
+
X
0
mit
0
0
0
0
0
0
0
0
fQ= < 0 0 jvj > (20 ) , (20 ) < 0 0 jvj > Q= g
0
0
(14.25)
0
0
0
0
0
0
0
Q= = , , ;
und dem Einteilchen-Hamiltonoperator (vgl. (14.17))
0
0
0
0
0
h =< jtj > + < jU 0j > +
0
X
0
(14.26)
0
< 0jvj >A :
0
0
0
(14.27)
In (14.25) haben wir dabei alle Matrixelemente von der Ordnung v c2 vernachlassigt
(Born'sche Naherung), was durchaus legitim ist, wenn wir uns entweder auf schwache
Restwechselwirkungen v(12) oder Fermionensysteme geringer Dichte beschranken. Weiterhin wurde benutzt
(20) = , = A 0
0
0
0
0
0
0
0
(14.28)
und
< jvj0 0 >A=< jvj0 0 > , < jvj 00 >
(14.29)
fur das antisymmetrische Matrixelement der Wechselwirkung v:
Die Gleichungen (14.24) und (14.25) bilden den Ausgangspunkt fur die weiterhin zu betrachtenden kinetischen Theorien; sie sind vollstandig antisymmetrisch in den Matrixelementen, geschlossen in und c2 und erlauben die quantenmechanische Beschreibung
von Fermionsystemen geringer Dichte oder schwacher Restwechselwirkung weit ab vom
Gleichgewicht. Wie im nachsten Abschnitt zu zeigen sein wird, erfullen sie die Erhaltungssatze von Fermionenzahl, Impuls, Drehimpuls sowie totaler Energie.
14.4 Erhaltungssatze
i) Teilchenzahlerhaltung
Die Teilchenzahl des Systems ist gegeben durch die Spur von oder in der diskreten Basis
durch
X
N (t) = (t):
(14.30)
Ableiten nach der Zeit und Einsetzen der Bewegungsgleichung fur (t) ergibt
d N (t) = X _ (t) = , i fX[h , h ]
(14.31)
dt
h +
[< jvj > C , C < jvj >]g = 0;
X
140
wie man leicht durch Umbenennen der Summationsindizes sieht. Damit ist die Teilchenzahl immer eine Erhaltungsgroe.
ii) Impuls- (Drehimpuls)-Erhaltung
Der Erwartungswert des Gesamtimpulses des Systems ist gegeben durch
< P >= Sp(p ) =
< jp j >=
X
X
< jpj > ;
(14.32)
da der Impuls p ein Einteilchenoperator ist. Zum Beweis der Impulserhaltung bildet man
die Zeitableitung von (14.32) und setzt erneut die Bewegungsgleichung fur (t) ein;
X
(14.33)
ih dtd < P >= < jpj > ih _
=
+
X
< jpj > [h , h ]
X
0
0
0
0
0
< jpj > [< jvj0 > C , C < 0 jvj >] = 0;
0
0
0
wie man erneut durch Umbenennen der Summationsindizes zeigt. Analog zum Impuls P
beweist man auch die Erhaltung des Gesamtdrehimpulses L, der sich aus der Summe der
Einteilchendrehimpulse li zusammensetzt, unter der Voraussetzung [v; li] = 0:
iii) Energieerhaltung
Fur jedes abgeschlossene System (hier U 0 0) mu die Gesamtenergie eine Erhaltungsgroe darstellen. Sie setzt sich zusammen aus der kinetischen Energie
X
Ekin =
< jtj > ;
(14.34)
der Energie des Mittleren Feldes
EMF = 21
X
0
0
< 00jvj >A ;
(14.35)
< jvj00 > C :
(14.36)
0
0
sowie der Korrelationsenergie
EKor = 21
X
0
0
0
0
Da die Gesamtenergie ein Zweiteilchenoperator ist, benotigt man nun zum Beweis der
Energieerhaltung die explizite Bewegungsgleichung fur die Matrixelemente von C ,
d.h.
d E = d fE + E + E g
(14.37)
dt
dt kin MF Kor
X
X
= < jtj > _ + 1
< 00 jvj >A [_ + _ ]
2
0
0
0
0
141
0
0
0
0
+ 21
X
0
0
< 00jvj > C_ = :::: = 0;
0
0
wie durch Einsetzen von _ aus (14.24) und C_ aus (14.25) nach kurzerer Rechnung ersichtlich wird. Damit ist auch die Energie fur alle Zeiten eine Erhaltungsgroe im Rahmen der
gekoppelten Gleichungen (14.24) und (14.25).
Bemerkung: Die hier gezeigten Erhaltungssatze gelten auch fur die nicht- storungstheoretischen gekoppelten Gleichungen (14.20) und (14.21) (in denen Terme der Ordnung v c2
nicht vernachlassigt werden), die vor allem in der Physik der starken Wechselwirkung eine
besondere Rolle spielen.
14.5 Die Vlasov Gleichung
Um den physikalischen Gehalt der Gleichungen (14.24) und (14.25) naher zu verdeutlichen, betrachten wir zunachst Gleichung (14.24) im Grenzfall C 0, d.h.
0
0
@ + i [ h , h ] = 0;
@t h X
0
0
0
(14.38)
und transformieren auf die Ortsdarstellung (x; x0 ; t) =< xj(t)jx0 > : Um die Notation
zu vereinfachen, lassen wir im folgenden (wie in (14.38)) die expliziten Indizes fur Spin
(Isospin etc.) weg, da sie fur die physikalischen Betrachtungen zunachst ohne Bedeutung
sind.
Weiterhin beschranken wir uns auf lokale Potential U (x; t), die sowohl aus einem aueren
Feld U 0 (x; t) bestehen konnen als auch durch die Selbstwechselwirkung der Fermionen
U s(x; t) (siehe (14.17)),
U (x; t) = U 0 (x; t) +
Z
X
Spin; Isospin
d3x2 v(x , x2 )(x2 ; x2; t);
(14.39)
wobei der Austauschterm der Wechselwirkung (Fock-Term) der Einfachheit halber vernachlassigt wurde.
In der Ortsraumdarstellung fur lokale Potentiale U (x; t) lautet (14.38) wie folgt,
@ (x; x0 ; t) + i f h 2 r2 + U (x; t) , h 2 r2 , U (x0 ; t)g(x; x0; t) = 0;
(14.40)
@t
h 2m x
2m x
was das Verstandnis allerdings noch nicht sonderlich erleichtert. Zweckmaigerweise transformiert man noch auf die Phasenraumdarstellung mittels einer Wigner-Transformation
(r; p; t) = d3s exp( hi p s) (r + s=2; r , s=2; t)
(14.41)
mit
x = r + s=2; x0 = r , s=2 oder r = (x + x0 )=2; s = x , x0 :
(14.42)
0
Z
142
Die quantenmechanische Phasenraumdichte (r; p; t) geht im klassischen Grenzfall uber
in die Wahrscheinlichkeit, ein Teilchen am Ort r mit Impuls p zur Zeit t zu nden.
Unabhangig vom klassischen Limes liefert die Integration von (14.41) uber den Impuls
Z
1
(14.43)
(r; t) = (2h )3 d3p (r; p; t)
die Ortsraumdichte (r; t), wahrend Integration uber den Ort die Impulsraumdichte (p; t)
liefert,
Z
(p; t) = d3r (r; p; t);
(14.44)
der Faktor 1=(2h )3 = h,3 in (14.43) ist dabei verantwortlich fur die Quantisierung im
Phasenraum pro intrinsischem Freiheitsgrad der Teilchen (Spin, Isospin, etc).
Bemerkung: Die Wignertransformierte (14.41) ist fur quantenmechanische Systeme im
allgemeinen nicht eine positiv denite Funktion auf den reellen Zahlen, sondern ein hermitescher Operator mit komplexen Werten in der Phasenraumdarstellung. Fur Systeme
hinreichend groer Teilchenzahl werden allerdings die Imaginarteile von (r; p; t) beliebig
klein, so da man von einer Annaherung an den klassischen Grenzfall sprechen kann.
Fuhrt man nun eine Wignertransformation von (14.40) durch, so erhalt man nach wenigen
Zeilen unter Verwendung von r2r+s=2 , r2r,s=2 = 2rs rr und partieller Integration [U B]:
@ (r; p; t) + p r (r; p; t)
@t
m r
(14.45)
[U (r + s=2) , U (r , s=2)] s rrU (r)
(14.46)
+ i d3s exp( i p s)[U (r + s=2; t) , U (r , s=2; t)] (r + s=2; r , s=2; t) = 0:
h
h
Diese Gleichung ist aufgrund der Unitaritat der Wigner Transformation aquivalent zu
(14.40). In (14.45) kann man nun fur den Fall kleiner 3. Ableitungen von U (r; t) im
Ortsraum die Naherung
Z
einsetzen | was fur den harmonischen Oszillator exakt ist | und erhalt nach partieller
Integration die Vlasov Gleichung:
@ (r; p; t) + p r (r; p; t) , r U (r; t) r (r; p; t) = 0:
(14.47)
r
p
@t
m r
Sie ist aquivalent zu
d = 0 = f @ + r_ r + p_ r g (r; p; t);
(14.48)
r
p
dt
@t
woraus durch Vergleich mit (14.47) die klassischen Bewegungsgleichungen fur r_ und p_
folgen,
(14.49)
r_ = mp ; p_ = ,rrU (r; t):
143
Folglich ist im Limes A ! 1 die Distribution
N A
t (r; p; t) = A1 (r , ri(t))(p , pi(t))
X
(14.50)
i=1
eine Losung der Vlasov Gleichung (14.47), falls ri(t), pi (t) Losungen der klassischen Bewegungsgleichungen (14:49) sind.
Der Ansatz (14.50) mit (14:49) wird in der Physik allgemein als Testteilchen-Methode
bezeichnet und erlaubt die dynamische Simulation von Vielteilchensystemen in einem
zeitabhangigen (selbstkonsistenten) mittleren Feld U (r; t), das durch die ZweiteilchenWechselwirkung v(r , r2) in (14.39) aufgebaut wird.
Wie man leicht zeigt, erhalt die Vlasov Gleichung wiederum die Teilchenzahl, den Gesamtimpuls und Drehimpuls sowie die totale Energie. Allerdings werden Relaxationsphanomene im Rahmen von (14.47) nicht korrekt beschrieben, da diese vorwiegend auf den hier
vernachlassigten 2-Teilchen Korrelationen beruhen.
14.6 Der Stoterm nach Uehling-Uhlenbeck
Wahrend die Ableitung der Vlasov Gleichung in Kap. 14.5 noch relativ einfach durchzufuhren war, erfordert der Stoterm in (14.20)
I (110; t) := , hi Sp(2=2 ) [v(12); c2(12; 1020; t)]
(14.51)
oder in einer Einteilchenbasis
XX
f< jvj > C , C < jvj0 >g
(14.52)
I (t) = , hi
0
0
0
die explizite Kenntnis der 2-Teilchen Korrelationsfunktion in einer beliebigen Basis j > :
Zu ihrer Berechnung verwenden wir zunachst zweckmaigerweise eine diskrete Basis, in
der der Einteilchen-Hamiltonoperator h (t) sowie insbesondere (t) diagonal ist, d.h.
0
h (t) (t) ; (t) = n (t) :
0
(14.53)
0
In dieser Basis reduziert sich die Bewegungsgleichung fur die Entwicklungskoezienten
C (t) nach (14.25) zu:
(14.54)
fih @t@ , [ + , , ]gC (t)
X
= f< jQ=vj > (20 ) , (20 ) < jvQ=j0 0 >g
0
0
0
0
0
0
0
0
=< jvj0 0 >A [n n (1 , n , n ) , n n (1 , n , n )]
=:< jVB (t)j0 0 >;
0
0
0
144
0
wobei wir ausgenutzt haben, da Q= in dieser Basis ebenfalls diagonal wird,
Q= = [1 , n , n ]:
(14.55)
Gleichung (14.54) ist eine Dierentialgleichung 1. Ordnung in der Zeit, die direkt integriert werden kann. Im Hinblick auf spater (im Rahmen der Energieerhaltung von 2Teilchenstoen) durchzufuhrende Naherungen setzen wir im folgenden bereits voraus, da
insbesondere die Einteilchenenergien (t) schwach veranderliche Funktionen der
Zeit sind. { Diese Naherung ist insbesondere fur die Elektronenzustande in Festkorpern
wie auch fur die Einteilchenzustande in einem hinreichend groen Normierungsvolumen
sehr gut bzw. exakt erfullt. { Fur eine verschwindende homogene Losung von (14.54) ist
C (t) dann gegeben durch
Z t
i
C (t) = , h
dt0 expf, hi [ + , , ](t , t0 )g < jVB (t0)j0 0 >; (14.56)
,1
wie man leicht durch Einsetzen in (14.54) veriziert.
Fur die Diagonalelemente des Stoterms (14.52) erhalten wir mit (14.56)
XX
f< jvj > C , C < jvj >g
(14.57)
I (t) = , hi
Z t
XX
1
=, 2
dt0 fexpf, hi [ + , , ](t , t0)g
h ,1
< jvj >< jVB (t0 )j >
, expf, hi [ + , , ](t , t0)g < jVB (t0)j >< jvj >g
Z t
XX
1
= 2
dt0 2 cosf h1 [ + , , ](t , t0 )g
h ,1
< jvj >< jvj >A [n(t0 )n (t0 )n(t0 )n (t0 ) , n (t0 )n (t0)n (t0)n (t0)]
0
0
0
0
0
0
mit n (t0 ) = 1 , n (t0) und VB (t0) aus (14.54).
Der letztere Ausdruck lat sich weiterhin auswerten unter der Annahme, da die Besetzungszahlen n(t0 ) n (t) schwach veranderliche Funktionen der Zeit sind. In diesem
Fall kann man fur Systeme geringer Dichte oder schwacher Restwechselwirkung die Zeitintegration in (14.57) durchfuhren und erhalt mit
Z t
dt0 cos( h1 [ + , , ](t , t0)) h ( + , , )
(14.58)
,1
die Energieerhaltung im 2-Teilchensto. | Anschaulich bedeutet (14.58), da die Zeit
zwischen zwei aufeinanderfolgenden Stoen s gro ist im Vergleich zu der konkreten
Stozeit c, so da die mit dem Sto verknupfte Energieunscharfe h =s hinreichend
klein wird. | Fur die Diagonalelemente des Stoterms erhalten wir damit
XX
I (t) 2h
( + , , ) < jvj >< jvj >A
(14.59)
145
[nn n n , nn n n ](t)
in der Basis j >; welche die Einteilchendichtematrix diagonalisiert.
Die weitere Auswertung von (14.59) fuhren wir nun durch fur hinreichend ausgedehnte
Systeme in der Basis ebener Wellen j > expfip rg, so da die Dichtematrix diagonal
im Impuls h p wird;
0
(p; p0 ) =
Z
d3 r expfi(p , p0) rg '(p)'(p0 ) = (2)3(p , p0)n(p):
(14.60)
In (14.60) hat damit n(p) die physikalische Bedeutung einer Besetzungswahrscheinlichkeit
fur den Zustand mit Wellenzahl p (oder Impuls h p):
Weiterhin nehmen wir der Einfachheit halber an, da die Matrixelemente der Wechselwirkung v in (14.59) unabhangig vom Spin (und Isospin ) sind als auch Spin und Isospin
nicht andern, d.h. in der Ortsraumdarstellung gelte:
< r1r21 2 1 2jvj1 2 1 2 r1 r2 >= 1 1 2 2 1 1 2 2
0
0
0
0
0
0
0
0
0
(14.61)
0
(r1 , r1 )(r2 , r2 )v(r1 , r2 );
0
0
oder in der Impulsraumdarstellung
< p1p2 1 2 1 2jvj1 2 1 2 p1 p2 >= 1 1 2 2 1 1 2 2
0
0
0
0
0
0
0
0
0
0
(14.62)
(2)3(p1 + p2 , p1 , p2 )v(p2 , p2 );
0
0
0
welche die Impulserhaltung im 2-Teilchensto zum Ausdruck bringt.
Unter den obigen Annahmen konnen wir den Ausdruck (14.59) unmittelbar auswerten
und erhalten mit (p) = h 2=2m p2
Z
2
1
I (p1; p1 ; t) = h (2s + 1)(2 + 1) (2)9 d3p2 d3p3d3p4
(14.63)
2
( 2hm [p21 + p22 , p23 , p24 ])(p1 + p2 , p3 , p4 )(2)6(p3 + p4 , p1 , p2 )v(p2 , p4 )vA (p4 , p2 )
fn(p3 ; t)n(p4 ; t)n(p1; t)n(p2 ; t) , n(p1 ; t)n(p2; t)n(p3 ; t)n(p4 ; t)g:
Gleichung (14.63) beschreibt Streuprozesse p1 +p2 ! p3 +p4 ('loss'-Term) sowie p3 +p4 !
p1 + p2 ('gain'-Term) unter Energie- und Impulserhaltung (siehe Skizze):
Weiterhin durfen die durch die Impulse p3 , p4 beschriebenen Endzustande (fur die 'loss'Terme) bzw. p1 , p2 (fur die 'gain'-Terme) nicht vollstandig besetzt sein aufgrund der
Faktoren n(pi ; t), welche das Pauli Prinzip fur Fermionen beinhalten.
Die Faktoren (2s + 1) fur die Summation uber Spin von Teilchen 2 und (2 + 1) fur die
Summation uber Isospin (oder weitere innere Freiheitsgrade) von Teilchen 2 fassen wir
zusammen in einen Faktor g; im Falle von Elektronen haben wir (s = 1=2, = 0) g = 2,
wahrend fur Nukleonen (s = 1=2, = 1=2) g = 4 resultiert.
146
Beispiel fur einen Stoprozess p1 + p2 ! p3 + p4 im Schwerpunktsystem unter
Erhaltung von Energie und Impuls.
Der Zusammenhang mit 2-Teilchenstreuprozessen wird unmittelbar deutlich, wenn wir das
Produkt v vA mit dem dierentiellen Wirkungsquerschnitt d=d
in Born'scher Naherung
(vgl. Quantentheorie) in Verbindung bringen,
d (p + p ; p , p ) = m2 v(p , p )v (p , p );
(14.64)
d
1 2 2 4 (162h 4) 2 4 A 4 2
was auf
Z
2 3
(14.65)
I (p1 ; p01; t) = (2)3(p1 , p01) 16m 2h (2g)5 d3p2d3p3 d3p4
2
( 2hm [p21 + p22 , p23 , p24 ]) (p1 + p2 , p3 , p4 ) dd
(p1 + p2 ; p2 , p4)
fn(p3; t)n(p4 ; t)n(p1 ; t)n(p2 ; t) , n(p1 ; t)n(p2 ; t)n(p3 ; t)n(p4; t)g
fuhrt, wobei wir in einer der beiden -Funktionen im Impuls die Hilfsvariable p01 eingefuhrt
haben. Gleichung (14.65) lat sich weiter vereinfachen, indem wir (nach Transformation
auf Relativ- und Schwerpunktsimpulse) uber die -Funktionen in (14.65) integrieren. Mit
dem Betrag der Relativgeschwindigkeit
h jp , p j
v12 = m
(14.66)
1
2
erhalten wir schlielich [U B]
I (p1 ; p01; t) = (2)3(p1 , p01) (2g )3 d3p2 d
v12 dd
(p1 + p2; p2 , p4) (14.67)
fn(p3 ; t)n(p4 ; t)n(p1; t)n(p2 ; t) , n(p1 ; t)n(p2; t)n(p3 ; t)n(p4 ; t)g;
wobei den Streuwinkel im Schwerpunktsystem bezeichnet und zu beachten ist, da
die Impulse p3 und p4 nach wie vor uber Energie- und Impulserhaltung mit p1 und p2
verknupft sind.
Z
Z
147
Den U bergang von der hier untersuchten Impulsraumdarstellung zur Phasenraumdarstellung (siehe Kap. 14.5) erfolgt nun durch eine inverse Wigner- Transformation,
Z
I (r; p; t) = (21)3 d3q expfiq rgI (p + q=2; p , q=2; t)
(14.68)
Z
= d3q expfiq rg(q)Icoll(p; t) = Icoll (p; t)
Z
Z
g
3
= (2)3 d p2 d
v12 dd
(p1 + p2 ; p2 , p4 )
fn(p3 ; t)n(p4 ; t)n(p1; t)n(p2 ; t) , n(p1 ; t)n(p2; t)n(p3 ; t)n(p4 ; t)g;
womit wir das Endresultat fur alle weiteren Anwendungen erreicht haben.
Im Falle des thermodynamischen Gleichgewichts (fur t ! 1), d.h. Icoll (p; t) ! 0 fur alle
p, erfullt die Fermi Verteilung n() (11.1) die notwendige Bedingung
fn(p3; t)n(p4 ; t)n(p1 ; t)n(p2 ; t) , n(p1 ; t)n(p2 ; t)n(p3 ; t)n(p4; t)g = 0
(14.69)
und ist damit Losung von (14.68) fur Icoll = 0:
Beweis: 2
Mit (p) = h =2m p2 und die fur die Fermi Verteilung fur alle und gultige Identitat
f ( , )g
n () = 1 , n() = 1 +expexp
f ( , )g
(14.70)
fuhrt (14.69) auf die Bedingung
expf ((p1 ) , )g expf ((p2 ) , )g , expf ((p3) , )g expf ((p4) , ) = 0; (14.71)
welche aquivalent ist zu
expf ((p1) + (p2 ))g = expf ((p3 ) + (p4 )g:
(14.72)
Diese letztere Indentitat ist nach (14.65) jedoch aufgrund der Energieerhaltung im 2Teilchensto (d.h. ((p1)+ (p2 ) , (p3 ) , (p4 ))) immer erfullt, womit die obige Aussage
bewiesen ist.
14.7 Die Vlasov-Uehling-Uhlenbeck Gleichung
Mit den Ergebnissen von Kap. 14.5 und Kap. 14.6 konnen wir nun den semiklassischen
Limes der Gleichung (14.24) in der Phasenraumdarstellung angeben, wenn wir n(p; t)
mit der lokalen Phasenraum-Besetzungswahrscheinlichkeit (r; p; t) bei hinreichend ausgedehnten Systemen identizieren. Die Kombination der Vlasov Gleichung (14.47) und
des Stoterms Icoll (14.68) liefert dann die Vlasov-Uehling-Uhlenbeck (VUU) Gleichung,
148
die in der Literatur auch unter den Namen Vlasov-Nordheim oder Boltzmann-UehlingUhlenbeck Gleichung bekannt ist,
(14.73)
f @t@ + pm1 rr , rrU (r; t) rp1 g(r; p1; t) = Icoll(r; p1 ; t)
Z
Z
= g 3 d3p2 d
v12 d (p1 + p2 ; p2 , p4 )
(2)
d
f(r; p3; t)(r; p4 ; t)(r; p1; t)(r; p2; t) , (r; p1; t)(r; p2; t)(r; p3; t)(r; p4; t)g;
welche die Zeitentwicklung eines Systems von Fermionen unter dem Einu eines zeitabhangigen selbstkonsistenten mittleren Feldes U (r; t) sowie Energie- und Impulserhaltenden
2-Teilchenstoen beschreibt. Sie dient als Ausgangsbasis fur verschiedene TestteilchenSimulationen in der Festkorper-, Atom- und Kernphysik und hat entscheidend zum Verstandnis der Dynamik von Fermi-Systemen weit ab vom Gleichgewicht beigetragen.
Bemerkung:
Im Falle von klassischen Teilchen vereinfacht sich (14.73) insoweit, da die Pauli-Blocking
Faktoren (r; pi; t) = 1 gesetzt werden und die Antisymmetrisierung im Wirkungsquerschnitt (14.64) vernachlassigt wird. Die weitere Naherung rrU (r; t) = 0 liefert dann die
Boltzmann Gleichung
f @ + p1 r g(r; p ; t) = g
@t
m
r
1
(2)
Z
3
d p2 d
v12 dd
(p1 + p2)
3
Z
(14.74)
f(r; p3; t)(r; p4; t) , (r; p1; t)(r; p2; t)g;
die zur Beschreibung der Dynamik klassischer Gasteilchen verwendet wird.
14.8 Storaten, mittlere freie Weglange
Um eine Abschatzung der Zeitskalen zu erhalten, die fur ein Erreichen der Gleichgewichtskonguration oder des statistischen Gleichgewichts notwendig sind, betrachten wir
den Spezialfall eines Teilchens mit Impuls p, welches in einem hinreichend (bzw. unendlich) groen und homogenen Fermi-System propagiert, das fur Temperatur T = 0 im
Impulsraum durch eine Fermikugel mit Radius pF dargestellt werden kann. Einen solchen
Fall kann man experimentell dadurch realisieren, da man entweder ein Elektron auf einen
metallischen Festkorper oder auch ein Proton auf einen groen Atomkern wie Pb schiet.
Die entsprechende Konguration im Impulsraum ist in der folgenden Skizze dargestellt:
Aufgrund der Homogenitat des Systems hangt die Phasenraumdichte nicht vom Ort r ab
und die A nderung der Besetzungszahl des Zustandes mit Impuls p aufgrund von Stoprozessen von p mit p2 wird beschrieben durch den 'loss'-Term
d n(p; t) = , g Z d3p Z d
v d (p + p ; p , p )
(14.75)
2
12
2
2
4
dt
(2)3
d
n(p; t)n(p2 )n(p3)n(p4);
149
Beispiel fur die Impulsraumkonguration bei der Streuung von einem Proton mit Impuls
p an einem 'Atomkern' mit Fermi-Impuls pF .
wobei die Ruckwirkung der Streuprozesse auf das System vernachlassigt wurde. Wegen
der Linearitat von (14.75) in n(p; t) konnen wir auch schreiben
d n(p; t) = , 1 n(p; t)
(14.76)
dt
r (p)
mit der Storate
Z
Z
r (p),1 = (2g )3 d3p2 d
v12 dd
(p + p2 ; p2 , p4 )n(p2 )n(p3)n(p4):
(14.77)
Die Groe r (p) wird auch als Relaxationszeit bezeichnet, da die Losung der DierentialGleichung (14.76) mit der Randbedingung n(p; t = 0) = 1 gegeben ist durch
n(p; t) = expf, (tp) g:
(14.78)
r
Die Relaxationszeit gibt daher an, innerhalb welcher Zeit ein Einteilchenzustand, der im
thermodynamischen Gleichgewicht nicht besetzt ist, uber Streuprozesse auf die Wahrscheinlichkeit 1=e abfallt.
Wie eine Betrachtung der obigen Skizze sofort verdeutlicht, ist wegen der Energierhaltung
in 2-Teilchenstoen bei der Temperatur T = 0 die Relaxationszeit r (p) = 1 fur alle
p < pF aufgrund des Pauli-Blockings, d.h. trotz moglicherweise starker Wechselwirkung
konnen die Teilchen im Grundzustand keine Stoe ausfuhren! Erst fur p > pF onet sich
der erlaubte Phasenraum und die Storate wachst quadratisch (ohne Beweis) mit der
Energie oberhalb der Fermienergie, d.h.
2
r ((p)),1 ((p),2 F )
(14.79)
F
mit F = h 2=2m p2F : Fur p pF schlielich verliert das Pauli-Blocking an Bedeutung und
wir erhalten das klassische Ergebnis fur die Storate mit v = p=m =< v12 >;
Z
Z
g
,
1
3
r (p) (2)3 v d p2 d
dd
(p)n(p2 )
(14.80)
150
= g 3v
(2)
Z
d3 p2 (p)n(p2 ) = v (p)
mit der Dichte = g=(62)p3F . Im klassischen Grenzfall ist { wie zu erwarten { die
Storate direkt proportional zur Relativgeschwindigkeit v, dem totalen Querschnitt und der Dichte des Systems.
Mit der fur homogene Systeme gultigen Relation,
d n(p; t) = v @ n(p; r);
(14.81)
dt
@r
erhalten wir alternativ
@ n(p; r) = , 1 n(p; r)
(14.82)
@r
(p)
mit der mittleren-freien-Weglange
(p) = (p1 )
(14.83)
fur klassische Teilchen.
Mit der VUU Gleichung (14.73) bzw. der Boltzmann Gleichung (14.74) ist damit der
Rahmen abgesteckt fur die Beschreibung von Fermi-Systemen bzw. klassischen Teilchen
weit ab vom Gleichgewicht bis hin zum thermodynamischen Gleichgewicht fur t ! 1.
Ohne expliziten Beweis sei noch das vergleichbare Ergebnis fur Bose-Systeme erwahnt:
man setze in (14.73) (r; p; t) = 1 + (r; p; t), wobei (r; p; t) in diesem Fall die Phasenraumdichte der Bosonen darstellt. In Analogie zu Gleichung (14.69) ergibt sich dann als
Gleichgewichtslosung die Bose-Verteilung (8.13).
151