1. Mengenlehre

1. Mengenlehre
Grundbegriffe
Definition
Eine Menge ist eine Zusammenfassung von
verschiedenen Elementen. Dabei muss genau festgelegt
sein, welche Elemente zu der Menge gehören.
Beispiele:
• Die Menge aller Buchstaben
• Die Menge aller ganzen Zahlen zwischen 2 und 10
„Vokabeln“
Symbol
Begriff
Erläuterungen/Sprechweisen
Mengenklammer
Für die Mengendarstellung in aufzählender und
beschreibender Form
G
Grundmenge
Menge der zur Verfügung stehenden Elemente für eine
bestimmte Aufgabenstellung
∈
Element
„… ist Element von …“
∉
nicht Element
„… ist nicht Element von …“
⊂
Teilmenge
„… ist Teilmenge von …“
∩
Schnittmenge
„… geschnitten mit …“
∪
Vereinigungsmen
ge
„… vereinigt mit …“
\
Restmenge
„… ohne …“
{…}
Merke
Mengen werden in der Regel mit großen Buchstaben benannt, A, B, C,
…
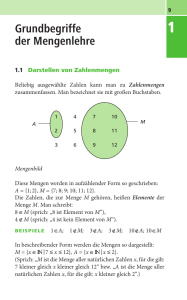
Mengen lassen sich auf drei verschiedene Weisen darstellen:
• Mengendiagramm (Mengenbild)
2 4 6
A
• Aufzählende Form
• Beschreibende Form
3 12 8 10
A = {2, 4, 6, 8, 10, 12}
A = {x |x ist gerade Zahl und kleiner als 13}
Aufgaben
• Stellen Sie die nachfolgenden Mengen als Mengenbild, in
aufzählender Form und in beschreibender Form dar:
a. die Menge der Buchstaben des Wortes „Kinderpflegerin“
b. die Menge der Buchstaben des Wortes „Hauswirtschaft“
c. die Menge der Lehrer Ihrer Klasse
d. die Menge der Zahlen zwischen 1 und 10
e. die Menge der Primzahlen zwischen 1 und 20
Aufgaben
• Die Grundmenge sei G = Menge aller Buchstaben des Alphabets.
Geben Sie als Mengenbild und in aufzählender Form an:
a. V = {x |x ist ein Vokal}
b. M = {x |x kommt in dem Wort Mathematik vor}
• Die Grundmenge sei G = Menge der natürlichen Zahlen. Schreiben Sie
in aufzählender Form:
c. Q = Menge aller zweistelligen Zahlen mit der Quersumme 10
Aufgaben
• Geben Sie folgende Mengen in beschreibender Form an:
a. B = {Januar, März, Mai, Juli, August, Oktober, Dezember}
b. C = {3, 4, 5, 6}
c. D = {3, 6, 9, 12, 15, 18}
Merke
• Will man ausdrücken, dass ein Element zu einer bestimmten Menge
gehört, benutzt man das Zeichen ∈. Gehört das Element nicht dazu,
wird das Zeichen ∉ verwendet.
A = {4, 5, 6}
4∈A
„4 ist Element der Menge A“
7∉A
„7 ist nicht Element der Menge A“
5∈A
„5 ist Element der Menge A“
Unterscheidung von Mengen nach der Menge
ihrer Elemente
• unendliche Menge: eine Menge mit einer unbegrenzten Anzahl von
Elementen
Beispiel: Menge der natürlichen Zahlen
A = {1, 2, 3, 4, …}
• endliche Menge: eine Menge mit einer begrenzten Anzahl von
Elementen
Beispiel: Menge der natürlichen Zahlen zwischen 4 und 7
B = {5, 6}
• leere Menge: eine Menge, die keine Elemente enthält
Beispiel: Menge der natürlichen Zahlen zwischen 5 und 6
C={}
Teilmenge
• Eine Menge B heißt Teilmenge einer Menge A, wenn jedes Element
von B auch Element von A ist.
B⊂A
{1, 3} ⊂ {1, 2, 3, 6}
denn alle Elemente von B
gehören auch zu A
6
1
3
B
A
2
Schnittmenge
• Die Schnittmenge A ∩ C zweier Mengen A und C ist die Menge aller
Elemente, die zu A und zu C gehören.
A = {1, 2, 3, 6}
C = {2, 3, 5, 7}
A ∩ C = {2, 3},
denn 2 und 3 sind genau
die Elemente, die sowohl
zu A als auch zu C gehören
Vereinigungsmenge
• Die Vereinigungsmenge A ∪ C zweier Mengen A und C ist die Menge
aller Elemente, die zu A oder zu C oder auch zu beiden gehören.
A = {1, 2, 3, 6}
C = {2, 3, 5, 7}
A ∪ C = {1, 2, 3, 5, 6, 7}
Restmenge
• Die Restmenge A \ C zweier Mengen A und C ist die Menge aller
Elemente, die nur zu A, aber nicht zugleich auch zu C gehören.
A = {1, 2, 3, 6}
C = {2, 3, 5, 7}
A \ C = {1, 6}
Aufgaben
• B sei die Menge der durch 7 teilbaren Zahlen. A sei die Menge der
Primzahlen zwischen 1 und 50.
a. Welche Mengenarten liegen vor?
b. Welche der folgenden Zahlen sind Elemente von A, welche von B?
9, 13, 7, 22, 17, 49, 50, 109, 36, 37
Aufgaben
• Sind die folgenden Mengen unendlich, endlich oder leer?
a. Menge aller Altenpflegeheime in Brandenburg
b. Menge der Buchstaben des Wortes „Kindergarten“
c. Menge der Schülerinnen dieser Klasse
d. Menge aller Multiplikationsaufgaben
e. Menge der Primzahlen zwischen 24 und 28
f. Menge alle Teiler von 24
Aufgaben (S. 15 Nr. 11)
• Geben Sie bei den folgenden Mengen jeweils die
Teilmengenbeziehungen an und begründen Sie.
a. A = Menge der Personen im Kindergarten X
B = Menge der Erzieherinnen im Kindergarten X
C = Menge der 5jährigen Mädchen im Kindergarten X
A
B
C
• Geben Sie bei den folgenden Mengen jeweils die
Teilmengenbeziehungen an und begründen Sie.
b) A = {2, 3, 4, 5}
B = {1, 2, 3, 4, …}
C = {2, 4, 6, 8}
3
5
B
A
2
4
6
8
C
• Geben Sie an, welche Teilmengenbeziehung zwischen den folgenden
Mengen besteht:
A = {1, 2, 3, 4, …}
B = {2, 4, 6, 8, …}
C = {4, 8, 16, 24, …}
A ⊂ A aber auch A ⊆ A
B ⊂ A, B ⊂ B, B ⊆ B
C ⊂ A, C ⊂ B, C ⊂ C, C ⊆ C
Grundmenge G
G = Menge der ungeraden Zahlen unter 10
A = Menge der Primzahlen
Übertragen Sie das Mengenbild in Ihr Heft. Ergänzen Sie die Elemente
der Grundmenge G und der Menge A.
9
1
G
3 5 7
A
G = {1, 2, 3, 4, 5, 6, 7, 8, 9}
A = Menge aller Primzahlen
B = Menge aller ungeraden Zahlen
C = Menge aller durch 3 teilbaren Zahlen
2
57
1
3
A
9
a) Schreiben Sie die Mengen in
aufzählender Form.
b) Übertragen Sie das Mengenbild und
ergänzen Sie die Elemente.
6
4
G
C
B
• Gegeben: G = {a, b, c, d, e}
A = {a, b, c}
B = {b, c}
C=
{c, d, e}
D = {b, c}
E = {a, b, c}
G
A
B
C
G⊂
A⊂
B⊂
C⊂
D⊂
E⊂
Tragen Sie in die Tabelle „wahr“ ein, wenn die angegebene Beziehung richtig ist.
Tragen Sie „falsch“ ein, wenn sie nicht richtig ist.
D
E
G
A
B
C
D
E
G⊂
wahr
falsch
falsch
falsch
falsch
falsch
A⊂
wahr
wahr
falsch
falsch
falsch
wahr
B⊂
wahr
wahr
wahr
falsch
wahr
wahr
C⊂
wahr
falsch
falsch
wahr
falsch
falsch
D⊂
wahr
wahr
wahr
falsch
wahr
wahr
E⊂
wahr
wahr
falsch
falsch
falsch
wahr
Welche Mengen sind „gegenseitig“ Teilmengen?
A ⊂ E und E ⊂ A
B ⊂ D und D ⊂ B
Welche Mengen enthalten dieselben Elemente und sind deshalb
gleiche Mengen?
A = E, B = D
Vervollständigen Sie nun die folgende Aussage: „Zwei Mengen sind
genau dann gleich, wenn … sie gegenseitig Teilmengen sind.“
Aufgaben
• Wie lauten die Schnittmenge, die Vereinigungsmenge und die
Restmenge A\B?
a. A = Menge aller Getränke
B = Menge aller Obstsäfte
b. A = {1, 2, 3, …, 100}
B = {9, 18, 27, …, 99}
c. A = Menge aller Teiler der Zahl 20
B = {1, 2, 4, 5, 10, 20}
Gesetze für Mengenverknüpfungen
A
B
1
2
6
3
4
5
7
C
A = {1, 2, 3, 4 }
B = {2, 3, 5, 6 }
C = { 3, 4, 5, 7}
a.
b.
c.
d.
A∪B=B∪A
{1, 2, 3, 4, 5, 6, 7} = {1, 2, 3, 4, 5, 6, 7}
A ∩ (B ∩ C) = (A ∩ B) ∩ C
{3} = {3}
A ∩ (B ∪ C) = (A ∩ B) ∩ (A ∩ C)
{2, 3, 4} = {2, 3, 4}
A ∪ (B ∩ C) = (A ∪ B) ∩ (A ∪ C)
{1, 2, 3, 4, 5} = {1, 2, 3, 4, 5}