Grundbegriffe der Mengenlehre

9
1
Grundbegriffe
der Mengenlehre
1.1 Darstellen von Zahlenmengen
Beliebig ausgewählte Zahlen kann man zu Zahlenmengen
zusammenfassen. Man bezeichnet sie mit großen Buchstaben.
1
4
7
10
2
5
8
11
3
6
9
12
A
M
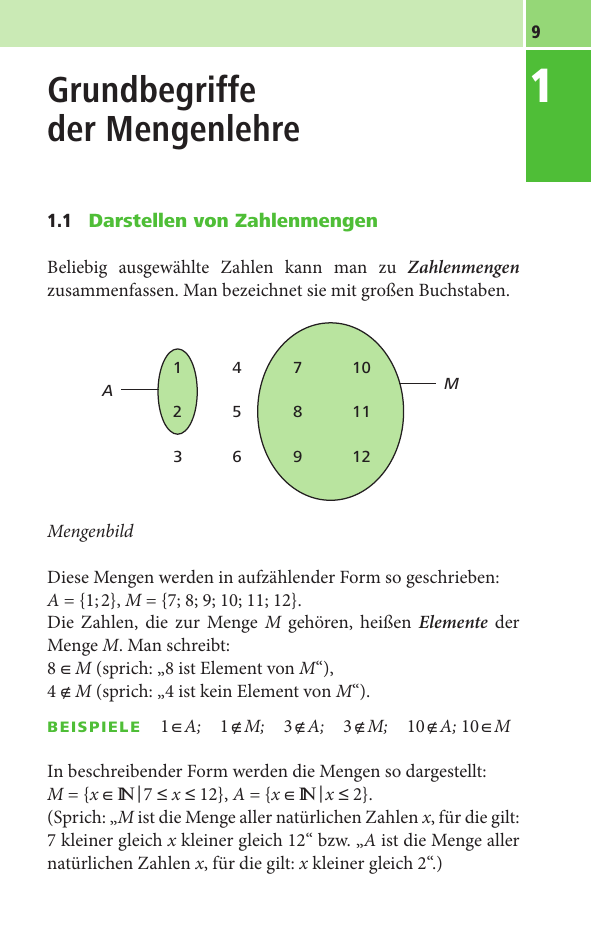
Mengenbild
Mengenbild
Diese Mengen werden in aufzählender Form so geschrieben:
A = {1; 2}, M = {7; 8; 9; 10; 11; 12}.
Die Zahlen, die zur Menge M gehören, heißen Elemente der
Menge M. Man schreibt:
8 ∊ M (sprich: „8 ist Element von M“),
4 ∉ M (sprich: „4 ist kein Element von M“).
Beispiele 1 ∊ A; 1 ∉ M; 3 ∉ A; 3 ∉ M; 10 ∉ A; 10 ∊ M
In beschreibender Form werden die Mengen so dargestellt:
M = {x ∊ N ∣ 7 ≤ x ≤ 12}, A = {x ∊ N ∣ x ≤ 2}.
(Sprich: „M ist die Menge aller natürlichen Zahlen x, für die gilt:
7 kleiner gleich x kleiner gleich 12“ bzw. „A ist die Menge aller
natürlichen Zahlen x, für die gilt: x kleiner gleich 2“.)
10
Grundbegriffe der Mengenlehre
1.2 Bezeichnungen
Die Anzahl der Elemente der Menge M heißt Mächtigkeit der
Menge M. Man schreibt: ∣ M ∣ (sprich: „Mächtigkeit von M“).
Beispiele
▪▪ M = {7; 8; 9; 10; 11; 12}, ∣ M ∣ = 6
▪▪ A = {1; 2}, ∣ A ∣ = 2
▪▪ ∣{1; 2; 3; 4}∣ = 4
Diese Mengen heißen endliche Mengen, da sie endlich viele Elemente besitzen. Mengen, die unendlich viele Elemente besitzen,
heißen unendliche Mengen. Wir geben in solchen Fällen mindestens die ersten fünf Elemente an und kennzeichnen durch
drei Punkte am Ende in der Mengenklammer, dass die Menge
unendlich ist.
Beispiele
▪▪ Die Menge der natürlichen Zahlen: N = {1; 2; 3; 4; 5; …}
▪▪ Die Menge der ungeraden Zahlen: U = {1; 3; 5; 7; 9; 11; …}
▪▪ Die Menge der geraden Zahlen: G = {2; 4; 6; 8; 10; 12; …}
Die Menge, die kein Element enthält, heißt leere Menge.
Man schreibt dafür { } oder ∅. Hier gilt: ∣ { } ∣ = 0.
1.3 Teilmenge
Eine Menge B heißt Teilmenge einer Menge A, wenn alle Elemente der Menge B auch zur Menge A gehören. Man schreibt:
B ⊂ A (sprich: „B ist Teilmenge von A“),
D ⊄ C (sprich: „D ist keine Teilmenge von C“).
Schnittmenge, Vereinigungsmenge, Restmenge
11
Beispiele
▪▪ A = {1; 2; 3; 4; 5; 6}
B = {2; 4; 6}
B⊂A
▪▪ C = {1; 2; 3; 4; 5}
A
1
3
5
B
2
4
6
D
D = {0; 1; 2}
D⊄C
C
0
1
3
2
4
5
  B e ac h t e Die Zeichen ⊂ und ⊄ stehen zwischen Mengen,
die Zeichen ∊ und ∉ zwischen Elementen und Mengen.
1.4 Schnittmenge, Vereinigungsmenge,
Restmenge
A = {1; 2; 3; 4; 6; 12}, B = {1; 2; 4; 8; 16}
Gemeinsames Mengenbild:
A
6
3
12
2
1
4
8
B
16
A ∩ B = {1; 2; 4}, A ∪ B = {1; 2; 3; 4; 6; 8; 12; 16}
A\B = {3; 6; 12}, B\A = {8; 16}
1
12
Grundbegriffe der Mengenlehre
Die Schnittmenge A ∩ B (sprich: A
„A geschnitten B“) enthält alle
Elemente, die zugleich zur Menge
A und zur Menge B gehören.
B
Die Vereinigungsmenge A ∪ B
(sprich: „A vereinigt B“) enthält
alle Elemente, die zur Menge A
oder zur Menge B gehören.
A
B
Die Restmenge A\B (sprich:
„A ohne B“) enthält alle Elemente,
die zur Menge A, aber nicht zur
Menge B gehören.
A
B
Grundbegriffe der Mengenlehre
13
Teste dein Wissen!
Kapitel
„Grundbegriffe der Mengenlehre“
O. K.
✔
Das muss ich
noch mal lesen
Ich kann Zahlenmengen in aufzählender
und in beschreibender Form angeben.
S. 9
Ich kann die Zeichen „∊“ und „∉“ erklären und sicher anwenden.
S. 9
Ich kann den Begriff Mächtigkeit erklären.
S. 10
Ich kann entscheiden, ob eine Menge
Teilmenge einer anderen Menge ist.
S. 10, 11
Ich kann zu zwei Mengen die Schnittund die Vereinigungsmenge bestimmen.
S. 11, 12
Ich kann zu zwei Mengen die Restmengen bestimmen.
S. 11, 12
Ich kann die Zeichen „⊂“„∩“„∪“ und „\“
erklären und sicher anwenden.
S. 11, 12
1