5 KRÄFTEGLEICHGEWICHT
Werbung

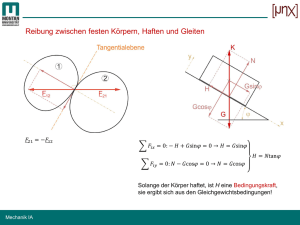
10TG - MECHANIK 5 KRÄFTEGLEICHGEWICHT P. Rendulić 2012 31 KRÄFTEGLEICHGEWICHT 5.1 Definition In einem gegebenen Bezugssystem ist ein Körper im Kräftegleichgewicht, wenn alle Punkte, die den Körper bilden, sich in diesem Bezugssystem nicht bewegen. 5.2 Zwei Kräfte stehen im Gleichgewicht 5.2.1 Versuch 9,8 N FKraftmesser FG FKraftmesser m = 1kg Wir befestigen ein Wägestück von 1 kg Masse an einem Kraftmesser. Wir stellen fest, dass das Wägestück sich im Kräftegleichgewicht befindet. Dabei wirken 2 gleich große Kräfte am Wägestück. Die Gewichtskraft zieht es nach unten und der Kraftmesser zieht es nach oben, wodurch es nicht fallen kann und sich im Gleichgewicht befindet. Wenn wir beide Kräfte addieren, so stellen wir fest, dass die resultierende Kraft null ergibt. 9,8 N FG 5.2.2 Formulierung der Gleichgewichtsbedingung r r Wirken die Kräfte F1 und F2 auf einen Körper, so befindet sich r r r dieser im Kräftegleichgewicht wenn F1 + F2 = 0 . Wenn Gleichgewicht herrscht dann gilt: • • • Beide Kräfte besitzen die gleiche Richtung und die gleiche Wirkungslinie. Beide Kräfte besitzen den gleichen Betrag. Beide Kräfte besitzen den entgegengesetzten Richtungssinn. r r r r Man sagt, dass F1 und F2 entgegengesetze Kräfte sind: F1 = −F2 . Dadurch ist ihre resultierende Kraft gleich Null. 5.2.3 F2 Anmerkung: F1 r r Unter dem Einfluss von F1 und F2 wird sich der Körper drehen; er befindet sich nicht im Gleichgewicht, denn beide Kräfte haben nicht die gleiche Wirkungslinie. Man sagt, dass beide Kräfte ein Drehmoment auf den Körper ausüben. Hätten beide Kräfte die gleiche Wirkungslinie, so wäre das dazugehörige Drehmoment gleich null. 10TG - MECHANIK 5.3 Drei Kräfte stehen im Gleichgewicht 5.3.1 Versuch Kräfteplan Krafteck F2 F1 F1 = 1,9 N F2 = 1,35 N 32 KRÄFTEGLEICHGEWICHT P. Rendulić 2012 F2 F1 FG FG FG = 1,96 N F1 F2 Wir befestigen einen Körper von 200 g Masse an 2 Kraftmessern. Wir stellen fest, dass sich der Körper im Kräftegleichgewicht befindet. Dabei wirken 3 Kräfte auf den Körper: r • Die Gewichtskraft FG zieht ihn lotrecht nach unten. r • Die Kraft F1 zieht ihn schräg nach links oben. r • Die Kraft F2 zieht ihn quer nach rechts. Wenn wir die am Körper wirkenden Kräfte maßstabstreu und winkeltreu addieren (parallel verschieben), so stellen wir fest, dass die resultierende Kraft null beträgt. Das dazugehörige Krafteck ist geschlossen. 5.3.2 Formulierung der Gleichgewichtsbedingung r r r Wirken die Kräfte F1 , F2 und F3 auf einen Körper, so befindet r r r r sich dieser im Kräftegleichgewicht wenn F1 + F2 + F3 = 0 Man kann den Zusammenhang auch folgendermaßen formulieren: Wenn ein Körper sich unter Einfluss von 3 Kräften im Kräftegleichgewicht befindet, dann bilden die Kraftpfeile ein geschlossenes Krafteck. 5.4 Allgemeiner Fall Versuche zeigen, dass die vorherigen Resultate verallgemeinert werden können: Ein Körper befindet sich im Kräftegleichgewicht, wenn die Summe aller auf ihn wirkender Kräfte gleich null ist. r r F ∑ =0 Die Kräfte bilden dabei ein geschlossenes Krafteck. Die Kräfteaddition wurde bereits behandelt. Wiederholung: Um Kräfte zu addieren, werden die Kraftpfeile so angereiht, dass jeweils die Pfeilspitze das Pfeilende des nächsten Pfeils berührt. 10TG - MECHANIK 5.4.1 P. Rendulić 2012 KRÄFTEGLEICHGEWICHT 33 Beispiele Bilderrahmen F2 F1 Wandkran F1 Kräfteplan F2 F2 FG F1 FG F1 FG Kräfteplan P F2 ^ 0,5 cm 10 N = FG Ein Bild von 3,77 kg Masse (Gewichtskraft: FG = 37 N) ist über 2 Fäden an einem Haken aufgehängt. Die Fadenkräfte können bestimmt werden, indem man vom Anfangs-, beziehungsweise r Endpunkt der Gewichtskraft FG ausgehend. Parallelen zu den Wirkungslinien der Haltekräfte einzeichnet. So findet man das geschlossene Krafteck und kann die Haltekräfte durch Vermessen der Kraftpfeile bestimmen. In diesem Fall gilt F1 = F2 = 35,5 N . ^ 1 cm 10 kN = Ein Wandkran trägt eine Last von 15 kN. Welche Kräfte müssen die Haltestangen aushalten? Im Punkt P greifen 3 Kräfte an: die r Gewichtskraft der Last FG , sowie die r r Stangenkräfte F1 und F2 . Alle Wirkungs– linien sind bekannt, somit können wir die Kraftpfeile im Kräfteplan parallel verschieben. r Wir zeichnen durch die Spitze von FG einen r Kraftpfeil parallel zur Wirkungslinie von F2 r und durch den Endpunkt von FG einen r Kraftpfeil parallel zur Wirkungslinie von F1 . Somit erhalten wir ein geschlossenes Krafteck und die Beträge der gesuchten Kräfte sind gegeben. Durch eine Messung finden wir: F1 = 27 kN und F2 = 17 kN . 10TG - MECHANIK KRÄFTEGLEICHGEWICHT P. Rendulić 2012 34 5.5 Zerlegen von Kräften Um Gleichgewichtssituationen zu analysieren, ist es oft sinnvoll, Kräfte entlang von gegebenen Richtungen zu zerlegen. Das heißt, dass eine Kraft in ihre Komponenten zerlegt wird (vom lat. componere = zusammensetzen). 5.5.1 Zerlegen einer Kraft in 2 Komponenten r Jede Kraft kann in 2 Komponenten zerlegt werden. Man fasst F r F als Diagonale eines Parallelogramms auf und zeichnet das Kräfteparallelogram mithilfe der Richtungen der Teilkräfte. Methode x1 F O x2 r Gegeben sind die Kraft F , die zerlegt werden soll, sowie die 2 Richtungen Ox1 und Ox2, nach denen die 2 Komponenten r r F1 und F2 gefunden werden sollen, sodass r r r F = F1 + F2 . x1 r Die Kraft F dient als Diagonale eines Parallelogramms von dem 2 Seiten sich auf den gegebenen Richtungen Ox1 und Ox2 befinden. F1 F O x2 F2 r r Physikalisch gesehen, rufen die Komponenten F1 und F2 genau die gleiche Wirkung r hervor wie die Kraft F . Man kann die Kraft also durch ihre Komponenten ersetzen, oder die Komponenten durch die Kraft ersetzen. 5.5.2 Sonderfall: die Kraftkomponenten stehen senkrecht zueinander r Ein Sonderfall liegt vor, wenn die Kraft F nach zwei senkrecht zueinander stehenden Richtungen Ox und Oy zerlegt wird. y F2 F Diese Situation ist interessant, weil sie rechnerisch einfach ist. F1 O x 10TG - MECHANIK P. Rendulić 2012 5.6 Aufgaben 5.6.1 Spaziergang mit Hunden KRÄFTEGLEICHGEWICHT 35 Eine Frau führt zwei Hunde spazieren. Bestimme die Kraft, welche die Frau aufbringen muss, damit die Hunde ihr nicht weglaufen. Auf der Zeichnung entspricht 1 cm Länge 100 N Kraft. 5.6.2 Aufgehängte Last C Eine Last von 100 N Gewicht wird durch 2 Seile AB und BC gehalten. Sie befindet sich im Gleichgewicht. A 30° 60° B 5.6.3 Gesucht sind die Kräfte, mit denen die Seile an der Mauer bzw. an der Decke ziehen. Straßenlaterne 80° 80° Eine Laterne der Masse 5 kg wird durch 2 Drahtseile gehalten, wie untenstehende Skizze zeigt. Wie groß ist die Spannung in den Seilen? 5.6.4 Bogenschütze Ein Bogenschütze spannt die Sehne eines Bogens mit der Kraft F = 120 N so weit, dass ihre beiden Hälften den Winkel θ = 140° miteinander bilden. Wie groß sind die Kräft e in der Sehne? (Skizze!) 10TG - MECHANIK 5.6.5 P. Rendulić 2012 Schild Ein Werbeschild der Masse 15 kg wird durch ein Drahtseil gehalten, wie nebenstehende Skizze zeigt. Wie groß ist die Spannung im Draht, und mit welcher Kraft drückt das Schild gegen die Wand? 5.6.6 KRÄFTEGLEICHGEWICHT 30° CAFE Kugel und Magnet Eine kleine Stahlkugel von 5 ⋅ 10 −2 N Gewicht hängt an einem dünnen Faden aus Nylon. Ein Magnet übt eine horizontale Anziehungskraft auf die Kugel aus, sodass der Winkel zwischen Mauer und Faden 20° beträgt. a. Wie groß ist die Anziehungskraft des Magneten? b. Wie groß ist die Spannung im Nylonfaden? S N 36 10TG - MECHANIK 6 37 ROLLEN UND FLASCHENZÜGE P. Rendulić 2012 ROLLEN UND FLASCHENZÜGE Ein Flaschenzug ist eine einfache Maschine, die den Betrag der aufzubringenden Kraft zum Bewegen oder Heben von Lasten verringert. Der Flaschenzug besteht aus festen und/oder losen Rollen sowie einem Seil oder einer Kette. 6.1 Beispiele aus dem Alltag Flaschenzug bei einem Kran. Rollenlose Flaschenzüge auf einem Boot. Spannvorrichtung für die Oberleitung bei der Eisenbahn. Flaschenzug zum Heben eines Schülers 6.2 Funktionsprinzip 5N 5N F = m·g 5N 5N 5N 5N m = 1kg 10N Um einen Körper zu heben, muss man eine Hubkraft aufbringen, welche vom Betrag her der Gewichtskraft des Körpers entspricht. 10N Eine einzelne Person kann Kraft sparen, indem der Körper zu zweit gehoben wird. Dabei kann der Körper auch teilweise durch eine Aufhängung festgehalten werden. 10N 10N Durch Anbringen von Rollen lässt sich der Körper auch heben. Da die Last an mehreren (hier 2) Seilstücken hängt, und nur eins von diesen angehoben wird, kann das Heben mit geringerer Kraft erfolgen. Die zum Heben aufzubringende Kraft kann noch weiter verringert werden, indem der Körper von noch mehr Seilstücken getragen wird. 10TG - MECHANIK 6.3 ROLLEN UND FLASCHENZÜGE P. Rendulić 2012 38 Versuche Feste Rolle Lose Rolle Flaschenzug 4N 4N 4N FZ FZ sZ sZ sZ FZ sL FL sL Bei einer festen Rolle ist die Zugkraft FZ genauso groß wie die Gewichtskraft der Last FL. Zugweg sZ und Lastweg sL sind gleich groß. FZ = FL sZ = sL FL Bei einer losen Rolle verteilt sich die Gewichtskraft der Last gleichmäßig auf 2 Seile. Die Zugkraft FZ ist daher nur halb so groß wie die Gewichtskraft der Last FL. Der Zugweg sZ ist doppelt so groß wie der Lastweg sL. FZ = 1 FL 2 sZ = 2 sL sL FL Bei einem Flaschenzug verteilt sich die Gewichtskraft der Last auf die Anzahl der tragenden Seile, in diesem Fall auf 4. Die Zugkraft FZ beträgt ein Viertel der Gewichtskraft der Last FL. Der Zugweg sZ ist viermal so groß wie der Lastweg sL. FZ = 1 FL 4 sZ = 4 sL Die angegebenen Formeln für die Kräfte gelten nur exakt, wenn die Masse der losen Rollen, sowie die Reibung vernachlässigbar sind. 10TG - MECHANIK ROLLEN UND FLASCHENZÜGE P. Rendulić 2012 39 6.4 Allgemeine Formulierung Um bei einem beliebigen Flaschenzug den Zusammenhang zwischen Zugkraft FZ und Lastkraft FL, sowie Zugweg sZ und Lastweg sL zu formulieren, reicht es die Anzahl n der tragenden Seile zu bestimmen. Beträgt die Anzahl der tragenden Seile bei einem Flaschenzug n, 1 so gilt: und s Z = n ⋅ sL FZ = ⋅ FL n n: Anzahl tragender Seilstücke 6.5 Arbeit beim Flaschenzug Man kann sich die Frage stellen, ob mit Hilfe eines Flaschenzugs Arbeit beim Heben eines Körpers gespart werden kann. Zur Veranschaulichung soll ein Körper einerseits ohne Flaschenzug, andererseits mit einem Flaschenzug senkrecht auf die Höhe h gehoben werden. In beiden Fällen soll die verrichtete Arbeit berechnet und verglichen werden. ► Fall 1 ► Fall 2 Der Körper wird senkrecht gehoben. Der Der Körper wird mit einem Flaschenzug Betrag der Hubkraft entspricht dem Betrag gehoben. der Gewichtskraft. n: Anzahl tragender Seile (hier: n = 4) FL mit: FZ= n FZ FHub sL= h FL sL= h Die verrichtete Arbeit beträgt: W1 = FHub ⋅ h = FG ⋅ h W1 = m ⋅ g ⋅ h sZ= n·h FL Die verrichtete Arbeit beträgt: F W2 = FZ ⋅ sZ = L ⋅ (n ⋅ h ) = FL ⋅ h = FG ⋅ h n W2 = m ⋅ g ⋅ h Wir stellen fest, dass in beiden Fällen die Arbeit gleich groß ist ( W1 = W2 )! Mit einem Flaschenzug kann keine Arbeit gespart werden! 10TG - MECHANIK ROLLEN UND FLASCHENZÜGE P. Rendulić 2012 40 6.6 Goldene Regel der Mechanik (erste Formulierung) Die vorherige Feststellung kann dazu genutzt werden die goldene Regel der Mechanik zu formulieren: Was man an Kraft spart, das muss man am Weg zulegen. Arbeit kann nicht gespart werden. 6.7 Weitere Flaschenzüge Potenzflaschenzug Differenzialflaschenzug ** r R 25 N FZ FZ sZ sZ 50 N 100 N sL sL FL FZ = FL 2n s Z = sL ⋅ 2 n n: Anzahl der losen Rollen Beim Potenzflaschenzug wird die Krafteinsparung ausschließlich mittels loser Rollen erzielt. Das Seil jeder Rolle ist an der Stütze und der nächsten Rolle befestigt. Während auf die untere lose Rolle noch die volle Lastkraft wirkt, wird diese beim unteren Seil schon halbiert. Am Seil der letzten Rolle wirkt schließlich die Zugkraft, die durch eine feste Rolle nach unten umgelenkt wird. Die Wirkung der losen Rollen potenziert sich. FZ = FL R − r ⋅ 2 R FL s Z = sL ⋅ 2⋅R R−r Der Differenzialflaschenzug besteht aus zwei fest miteinander verbundenen festen Rollen mit unterschiedlichen Durchmessern (r und R). Die Last hängt an einer losen Rolle. Bei diesem Flaschenzug wird ein durchgehendes Seil verwendet, in dem die Spannung nicht überall gleich ist. Durch die Anordnung wird das Drehmoment der kleinen Rolle dem der großen entgegen, sodass nur die Differenz als Zugkraft angewandt werden muss. Hinzu kommt die Halbierung der Lastkraft durch die lose Rolle. Je kleiner der Durchmesserunterschied zwischen den beiden Rollen ist, desto effektiver arbeitet der Differenzialflaschenzug. Ein wichtiger Vorteil dieses Flaschenzugs ist die Material- und Gewichtsersparnis. Da für die Funktion ein rutschfester Kontakt der beiden Seile mit den Rollen erforderlich ist, wird meistens anstatt eines Seils eine Kette verwendet die über verbundene Zahnräder läuft. 6.8 Reibungsverluste und Wirkungsgrad Alle bis jetzt genannten Formeln zur Berechnung der Zugkraft gelten nur unter der Voraussetzung, dass keine Verluste durch Reibung auftreten. In der Praxis sind die Reibungsverluste des Seils an den Rollen, bzw. die Reibung an den Rollen selbst, sowie 10TG - MECHANIK ROLLEN UND FLASCHENZÜGE P. Rendulić 2012 41 die Tatsache, dass die beweglichen Rollen, die untere Aufhängung und nicht zuletzt das Seil eine Masse besitzen, die mit angehoben werden muss, nicht zu unterschätzen. Es gilt daher: FZug Pr axis > FZug Theorie ** Der Wirkungsgrad des Flaschenzugs kann berechnet werden, indem der Quotient der nutzbaren Arbeit durch die zugeführte Arbeit berechnet wird: η= 6.9 Aufgaben 6.9.1 Flaschenzüge (1) (2) WNutz FL ⋅ sL = ** WZu FZ ⋅ sZ (3) (4) (5) (6) (7) Gib für die abgebildeten Flaschenzüge jeweils das Verhältnis zwischen der Zugkraft und der Lastkraft an! 10TG - MECHANIK 6.9.2 P. Rendulić 2012 ROLLEN UND FLASCHENZÜGE 42 Lastkran Eine Last wird mit Hilfe eines elektrischen Motors gehoben. Dieser wickelt ein Seil auf eine Trommel auf. Die Last soll um 3 m gehoben werden. Ihre Masse beträgt 120 kg, die Masse der losen Rolle beträgt 10 kg, die Masse des Motors beträgt 30 kg. a. Berechne die Zugkraft F1, die der Motor auf das Seil ausübt! b. Berechne den Kraftweg ∆s1! c. Wie groß ist die Last, die von der Schiene getragen wird ? 6.9.3 Flaschenzüge Berechne in jedem der Fälle A, B, C die aufzubringende Kraft, damit die Last im Gleichgewicht ist! Die Masse der Kiste beträgt 100 kg, die Masse des Menschen 80 kg. (A) 6.9.4 Baukran Ein Ingenieur will einen Baukran konstruieren. Der Kran soll eine maximale Last von 3 000 kg heben können. Verwendet wird ein Motor, der eine maximale Zugkraft von 6 500 N beim Aufwickeln eines Stahlseils aufbringen kann. a. Wie muss der Ingenieur vorgehen? b. Welche Leistung muss der Motor haben, wenn die Last in 50 Sekunden um 30 Meter gehoben werden soll? Gib die Leistung in PS an. c. Wie groß müsste die Leistung sein, wenn der Wirkungsgrad der Anlage nur 75% beträgt? * (B) (C) Gegengewicht Motor 10TG - MECHANIK P. Rendulić 2012 ROLLEN UND FLASCHENZÜGE 6.9.5 Duell Wer gewinnt das Duell? m1 = 95 kg m2 = 75 kg 43 10TG - MECHANIK P. Rendulić 2012 ROLLEN UND FLASCHENZÜGE 44 10TG - MECHANIK 7 P. Rendulić 2012 GENEIGTE EBENE 45 GENEIGTE EBENE Was ist einfacher? Ein schweres Bierfass auf die Ladefläche eines LKW’s zu heben, oder das Bierfass über eine Rampe auf die Ladefläche hinaufzurollen? Aus dem Alltag wissen wir, dass mit einer Rampe weniger Kraft aufgebracht werden muss. Durch einen Versuch und theoretische Überlegungen soll eine Formel hergeleitet werden, die es erlaubt den Betrag der Kraft zu bestimmen, die aufgebracht werden muss, um einen Körper mit der Hilfe einer Rampe zu heben. 7.1 Kräftediagramm Zur Analyse der Situation ist es sinnvoll, zu untersuchen, welche Kräfte an einem Körper (hier ein Wagen) wirken, der eine geneigte Ebene hinaufgezogen wird. FUnt. Wenn man davon ausgeht, dass die Reibungskräfte vernachlässigbar sind, dann wirken am Körper 3 Kräfte: r • FG : die Gewichtskraft des Körpers r • FZug : Kraft, mit welcher der Körper L FZug h FH FN α FG parallel zur Ebene hinaufgezogen wird, r • FUnt . : Kraft, mit welcher die Unterlage senkrecht gegen den Körper drückt. L bezeichnet die Länge der Ebene, h ist die Höhe der Ebene, α ist der Winkel zwischen der Horizontalen und der Ebene (Neigungswinkel oder Steigungswinkel). r Die Wirkung der Gewichtskraft FG kann in 2 senkrecht zueinander stehende Teile zerlegt r werden. Ein Teil von FG drückt senkrecht gegen die Unterlage. Dieser Kraftteil entspricht r der Normalkraft FN . Der andere Teil wirkt parallel zur Unterlage. Dieser Kraftteil r entspricht der Hangabtriebskraft FH . Diese Kraft ist dafür verantwortlich, dass der Körper beim Loslassen die Ebene hinunterrutscht und beschleunigt. Man kann schreiben: r r r FG = FN + FH * Wenn der Körper die Ebene mit konstanter Geschwindigkeit hinaufgezogen wird, dann ist die Hangabtriebskraft der Zugkraft entgegengesetzt. Beide Kräfte haben dann den gleichen Betrag: 10TG - MECHANIK GENEIGTE EBENE P. Rendulić 2012 r r FH = −FZug 46 FH = FZug und Zur Bestimmung der Hangabtriebskraft kann daher einfach die Zugkraft am Körper gemessen werden. 7.2 Versuch Es soll eine Formel zur Berechnung der Hangabtriebskraft exerimentell hergeleitet werden. 7.2.1 Versuchsdurchführung und Messwerte Für unterschiedlich schwere Körper wird der Betrag FH der Hangabtriebskraft in Abhängigkeit von der Länge L und der Höhe h der geneigten Ebene, sowie des Neigungswinkels α gemessen (→ Abbildung: siehe Abschnitt 7.1). Die Werte werden in eine Tabelle eingetragen. Länge der geneigten Ebene: L = ________ cm FG (N) h (cm) α (°) F H (N) h/L 7.2.2 Versuchsauswertung Der Versuch zeigt, dass: FH h = FG L und FH = sin α FG Durch eine Formelumstellung gilt für die Hangabtriebskraft: FH = FG ⋅ h L und FH = FG ⋅ sin α FH / FG sin α 10TG - MECHANIK GENEIGTE EBENE P. Rendulić 2012 47 Die Formeln zeigen: • FH ~ FG : • FH ~ h : • FH ~ 1 : L Wenn die Gewichtskraft (oder Masse) des Körpers verdoppelt wird, dann verdoppelt sich die Hangabtriebskraft. Wenn bei gleicher Länge die Höhe der geneigten Ebene verdoppelt wird, dann verdoppelt sich die Hangabtriebskraft. Wenn bei gleicher Höhe die Länge der geneigten Ebene verdoppelt wird, dann halbiert sich die Hangabtriebskraft. Die Hangabtriebskraft ist nicht proportional zum Neigungswinkel! • 7.3 Neigung und Steigung Man soll darauf achten, dass Neigung und Steigung unterschiedliche Größen sind. Die Neigung entspricht dem Quotienten aus Höhe und Länge der geneigten Ebene: Neigung = h L und h = sin α L Steigungen und Gefälle werden im Straßenverkehr in Prozent angegeben. Bei einer Steigung von 12 % gewinnt man 12 m an Höhe, wenn man in waagerechter Richtung 100 m zurücklegt. L h α Es gilt die Definition: b Steigung = h b und h = tan α b 7.3.1 Beispielwerte Die folgende Tabelle gibt die Neigung und den Neigungswinkel als Funktion der Steigung in Prozent an. Steigung (h/b in %) Steigung (h/b) Neigung (h/L) Steigungs– winkel (°) 0 0 0 0 5 0,050 0,050 2,9 10 0,100 0,099 5,7 15 0,150 0,148 8,5 25 0,250 0,243 14,0 50 0,500 0,447 26,7 100 1,000 0,707 45,0 500 5,000 0,980 78,7 Eine Steigung von 100 % entspricht einem Steigungswinkel von 45°. Entgegen der geläufigen Meinung entspricht eine Steigung von 100 % nicht einem Steigungswinkel von 90° (senkrecht nach oben)! 10TG - MECHANIK GENEIGTE EBENE P. Rendulić 2012 48 7.4 Arbeit an der geneigten Ebene Man kann sich jetzt die Frage stellen, ob an der geneigten Ebene Arbeit gespart werden kann. Zur Veranschaulichung soll ein Körper einerseits über eine geneigte Ebene, andererseits senkrecht auf die Höhe h gehoben werden. In beiden Fällen soll die verrichtete Arbeit berechnet und verglichen werden. ► Fall 1 ► Fall 2 Der Körper wird über die geneigte Ebene Der Körper wird senkrecht gehoben. Der gehoben. Der Betrag der Zugkraft Betrag der Hubkraft entspricht dem Betrag entspricht dem Betrag der der Gewichtskraft. Hangabtriebskraft. 1 2 L FHub h FZug α Die verrichtete Arbeit beträgt: h W1 = FZug ⋅ L = FH ⋅ L = FG ⋅ ⋅ L L W1 = m ⋅ g ⋅ h Die verrichtete Arbeit beträgt: W2 = FHub ⋅ h = FG ⋅ h W2 = m ⋅ g ⋅ h Wir stellen fest, dass in beiden Fällen die Arbeit gleich groß ist ( W1 = W2 )! An der geneigten Ebene kann keine Arbeit gespart werden! 7.5 Goldene Regel der Mechanik (zweite Formulierung) Die vorherige Feststellung kann dazu genutzt werden die goldene Regel der Mechanik zu formulieren: Was man an Kraft spart, das muss man am Weg zulegen. Arbeit kann nicht gespart werden. Die goldene Regel der Mechanik wurde bereits beim Flaschenzug kennengelernt. 10TG - MECHANIK 7.6 P. Rendulić 2012 GENEIGTE EBENE 49 Aufgaben 7.6.1 Kabelrolle Ein Bauarbeiter will eine Kabelrolle von 200 kg Masse um 2 m nach oben transportieren. Er kann beim Rollen maximal mit 500 N gegen die Rolle in Steigungsrichtung drücken. Welche Länge muss das Brett für die geneigte Ebene haben? 7.6.2 Geländewagen Der Geländewagen vom Typ Landrover Defender kann laut Herstellerangaben eine Steigung von 100 % bewältigen. a. Berechne die aufzubringende Antriebskraft, wenn die Masse des Fahrzeugs 2,8 Tonnen beträgt. b. Wie lange braucht das Fahrzeug um unter diesen Verhältnissen 100 m senkrecht zu steigen, wenn die maximale Motorleistung 120 PS beträgt? c. Welche Strecke ist das Fahrzeug dann gefahren? 7.6.3 Schrägaufzug Bei einem Schrägaufzug beträgt die zum Hochziehen eines gefüllten Wagens angesetzte Kraft 1 800 N. Bei einer Fahrbahnlänge von 20 m wird ein Höhenunterschied von 5 m überwunden. Welche gesamte Masse m kann ohne Berücksichtigung der Reibung mit konstanter Geschwindigkeit hochgezogen werden? 7.6.4 Bremsberg „am Wenschel“ Ab 1876 wurde am Beleserberg gefördertes Eisenerz über einen Bremsberg von der auf dem Hochplateau gelegenen Grube zur Ladestelle Wenschel gebracht. Bei dieser Beförderunggsart lagen zwei Gleise nebeneinander und der bergab, mit Erz beladene Förderwagen zog einen auf dem Parallelgleis laufenden leeren Förderwagen bergauf. Beide Förderwagen waren über ein langes Seil miteinander verbunden. Ab 1927 erwies der Bremsberg eine Steigung von 17,7 % bei einer Länge von 139,5 m auf (Quelle: Korspronk 20/2005). a. Worin liegt der Vorteil dieser Beförderungsart? b. Welche Bremskraft muss auf das Seil wirken, wenn der bergab fahrende Wagen mit 10 Tonnen Erz beladen ist? 10TG - MECHANIK 7.6.5 GENEIGTE EBENE P. Rendulić 2012 50 Geneigte Ebene und Flaschenzug Man möchte die folgende Anordnung benutzen, um einen Körper mit einer Kombination aus geineigter Ebene und Flaschenzug zu heben. Folgende Größen sind bekannt: L h • L=8m • m1 = 120 kg • m2 = 40 kg a. Berechne die maximale Höhe h, auf die der Körper m1 gehoben werden kann! Man geht davon aus dass die Reibung vernachlässigbar ist. Die Masse eines Rollenpaares mit Haken beträgt 6 kg. b. Wie ändert sich die Höhe h, wenn die Reibungskräfte berücksichtigt werden? m1 m2 7.6.6 Geneigte Ebene und Flaschenzug ** Ein Geländewagen steht auf einer geneigten, trockenen Straße aus Beton. Die Haftreibungszahl zwischen den Luftreifen und der Straße beträgt 0,55. a. Wie groß darf der Neigungswinkel der Straße maximal sein, damit der Wagen nicht ins Rutschen kommt? Wie groß ist dann die Steigung der Straße? b. Wie groß muss die Haftreibungszahl zwischen Reifen und Straße mindestens sein, damit der Wagen auf einer Straße mit 24 % Steigung sicher steht? α 7.7 Beispiele aus der Technik ◄ Serpentinen– straße ► Plan incliné d’Arzwiller 10TG - MECHANIK 8 P. Rendulić 2012 HEBEL UND DREHMOMENT 51 HEBEL UND DREHMOMENT 8.1 Hebel Ein Hebel ist ein Kraftwandler, bestehend aus einer steifen Stange, die um einen Drehpunkt bewegt werden kann. Meistens benutzt man ihn zum Verstärken von Kräften. Man unterscheidet zwischen dem zweiseitigen und dem einseitigen Hebel. 8.1.1 Zweiseitiger Hebel Beim zweiseitigen Hebel liegt der Drehpunkt innerhalb der Stange. Beispiele: Schraubenzieher zum Öffnen einer Farbdose Spielwippe Kneifzange 8.1.2 Einseitiger Hebel Beim einseitigen Hebel liegt der Drehpunkt an einem Ende der Stange. Beispiele: Nussknacker Schubkarre 8.1.3 Weitere Beispiele Die Photos zeigen weitere Beispiele aus dem Alltag. Entscheide jeweils selbst, um welche Hebelart es sich handelt! verschiedene Flaschenöffner Schraubschlüssel Bremshebel 10TG - MECHANIK HEBEL UND DREHMOMENT P. Rendulić 2012 8.2 Hebelgesetz beim zweiseitigen Hebel und 2 wirkenden Kräften 8.2.1 Versuch 52 An einer Seite des Hebels wird durch Anhängen einer Masse eine vertikale Kraft nach unten ausgeübt. An der anderen Seite wird an unterschiedlichen Stellen mit einem Kraftmesser nach unten gezogen sodass die Stange wieder horizontal (im rGleichgewicht) r steht. Gemessen werden die Beträge der beiden Kräfte F1 und F2 , sowie die dazugehörigen Hebelarme a1 und a2 . Darunter versteht man die Entfernung zwischen der Wirkungslinie der Kraft und dem Drehpunkt des Hebels. A a1 B a2 O m F2 F1 8.2.2 Messwertetabelle F1 (N) a1 (m) F2 (N) a2 (m) F1·a1 (N·m) F2·a2 (N·m) 8.2.3 Versuchsauswertung Zur Auswertung berechnen wir jeweils das Produkt aus Kraft und dem dazugehörigen Hebelarm. Wir stellen fest, dass das Produkt jeweils gleich ist. F1 ⋅ a1 = F2 ⋅ a2 Außerdem stellen wir fest: • • Je größer der Hebelarm ist, desto weniger Kraft braucht man, um den Hebel im Gleichgewicht zu halten. Je kleiner der Hebelarm ist, desto mehr Kraft braucht man, um den Hebel im Gleichgewicht zu halten. 10TG - MECHANIK P. Rendulić 2012 HEBEL UND DREHMOMENT 8.3 Hebelgesetz beim einseitigen Hebel und 2 wirkenden Kräften 8.3.1 Versuch 53 Am Hebel wird durch Anhängen einer Masse eine vertikale Kraft nach unten ausgeübt. An unterschiedlichen Stellen wird mit einem Kraftmesser nach oben gezogen sodass die Stange wiederr horizontal (im Gleichgewicht) steht. Gemessen werden die Beträge der r beiden Kräfte F1 und F2 , sowie die dazugehörigen Hebelarme a1 und a2 . A a2 a1 F2 B O m F1 8.3.2 Messwertetabelle F1 (N) a1 (m) F2 (N) a2 (m) F1·a1 (N·m) F2·a2 (N·m) 8.3.3 Versuchsauswertung Zur Auswertung berechnen wir jeweils das Produkt aus Kraft und dem dazugehörigen Hebelarm. Wir stellen fest, dass das Produkt jeweils gleich ist. F1 ⋅ a1 = F2 ⋅ a2 Wir stellen fest, dass das gefundene Hebelgesetz sowohl für den zweiseitigen als auch den einseitigen Hebel gilt. Da das Produkt aus Kraft und Hebelarm ausschlaggebend ist, wie groß die Drehwirkung einer Kraft ist, definieren wir im nächsten Abschnitt die physikalische Größe Drehmoment einer Kraft. 10TG - MECHANIK HEBEL UND DREHMOMENT P. Rendulić 2012 54 8.4 Drehmoment Eine Kraft kann bei einem drehbar gelagerten Körper eine Drehbewegung um den Drehpunkt hervorrufen. Die Wirkung der Kraft hängt dabei von ihrem Angriffspunkt ab. 8.4.1 Definition des Drehmoments Unter einem Drehmoment M versteht man das Produkt aus einer Kraft F und dem senkrechten Abstand a ihrer Wirkungslinie vom Drehpunkt O. M = F ⋅a 8.4.2 Hebelarm Den senkrechten Abstand zwischen der Wirkungslinie der Kraft und dem Drehpunkt bezeichnet man auch als Hebelarm. Die folgenden Beispiele zeigen wie der Hebelarm bestimmt wird: O a F O a a F F O 8.4.3 Einheit des Drehmoments Die SI-Einheit des Drehmoments ist das Newtonmeter (Nm): [M ] = [F ⋅ a] = 1N ⋅ 1m = 1Nm Das Newtonmeter darf man in diesem Fall nicht mit dem Joule gleichsetzen. Das Drehmoment hat in der Tat nichts mit der mechanischen Arbeit zu tun! 8.4.4 Spezialfälle * Der Versuch zeigt dass: • • • Eine Kraft, deren Wirkungslinie parallel zur Drehachse ist, bewirkt keine Drehbewegung. Eine Kraft, deren Wirkungslinie durch die Drehachse geht, bewirkt keine Drehbewegung. In beiden Fällen ist das Drehmoment dieser Kräfte null. 10TG - MECHANIK HEBEL UND DREHMOMENT P. Rendulić 2012 55 8.5 Hebel bei nicht senkrecht angreifenden Kräften Bei den bisherigen Beispielen standen die Wirkungslinie der Kraft und die Hebelstange jeweils senkrecht zueinander. In diesem Fall entspricht der Hebelarm einem Teil der Hebelstange. Man kann aber auch Kräfte in einem beliebigen Winkel zur Hebelstange wirken lassen: a2 A a1 B O m α F2 In diesem Fall entspricht der Hebelarm nicht mehr einem Teil der Hebel– stange sondern er liegt außerhalb von ihr und muss entweder graphisch oder durch eine Rechnung bestimmt werden. F1 r Der Versuch zeigt, dass je größer (oder kleiner) der Winkel α zwischen der Kraft F2 und der Hebelstange wird, desto größer muss der Betrag dieser Kraft gewählt werden, damit der Hebel im Gleichgewicht bleibt. In der Tat zeigt die Figur, dass in diesem Fall der Hebelarm a2 der Kraft kleiner wird. Dadurch wird natürlich auch das entsprechende Drehmoment kleiner. Damit der Hebel im Gleichgewicht bleibt muss der Betrag der Kraft erhöht werden. 8.5.1 Beispiel* r Für die folgende Versuchsanordnung soll der Betrag der Kraft F2 zuerst vorausgesagt werden und dann durch einen Versuch überprüft werden. C Das Hebelgesetz ergibt: F1 ⋅ a1 = F2 ⋅ a2 ⇔ F2 = F1 ⋅ a2 A a1=10cm β O Im Punkt B gilt: β + 130° = 180° ⇔ β = 50° B α=130° m=200g F2 L=25cm F1 a1 a2 Im rechtwinkligen Dreieck OBC gilt: a sin β = 2 ⇔ a2 = L ⋅ sin β L Schließlich können wir schreiben: a1 a1 = m⋅g ⋅ L ⋅ sin β L ⋅ sin β N 10 cm ⇔ F2 = 0,2 kg ⋅ 9,81 ⋅ kg 25 cm ⋅ sin 50° F2 = F1 ⋅ ⇔ F2 = 1,02 N Der Versuch zeigt, dass der experimentelle und der theoretische Wert übereinstimmen. 10TG - MECHANIK HEBEL UND DREHMOMENT P. Rendulić 2012 56 8.6 Allgemeines Hebelgesetz An einem beliebigen Hebel können auch mehrere Kräfte Drehmomente auf die Hebelstange ausüben. Es soll untersucht werden, wie das allgemeine Hebelgesetz in diesem Fall formuliert werden kann. 8.6.1 Versuch Wir versuchen am zweiseitigen Hebel ein Gleichgewicht herzustellen, indem wir bis zu 4 Massen an unterschiedlichen Stellen an die Hebelstange hängen. Wir bestimmen die Beträge der wirkenden Kräfte, sowie die dazugehörigen Hebelarme und tragen die Werte in die Tabelle ein. linksdrehend rechtsdrehend O a1 a2 F1 8.6.2 a4 a3 F2 F3 F4 Messwertetabelle Linksdrehende Kräfte Rechtsdrehende Kräfte F1 a1 F2 a2 F3 a3 F4 a4 (N) (m) (N) (m) (N) (m) (N) (m) 8.6.3 Versuchsauswertung Zur Auswertung berechnen wir jeweils die Summe der linksdrehenden Drehmomente Mlinks und die Summer der rechtsdrehenden Drehmomente Mrechs. Wir stellen fest, dass beide Werte jeweils gleich sind. Daraus formulieren wir das allgemeine Hebelgesetz, das für beliebig viele Kräfte gilt. 10TG - MECHANIK 8.6.4 HEBEL UND DREHMOMENT P. Rendulić 2012 57 Allgemeines Hebelgesetz Wenn der Hebel im Gleichgewicht ist, dann ist die Summe der linksdrehenden Drehmomente gleich der Summe der rechtsdrehenden Drehmomente. 8.6.5 Beispiel Das Beispiel zeigt den zweiseitigen Hebel mit Kräften, die senkrecht zur Hebelstange sind: rechtsdrehend O a1 F1 F2 a2 F3 linksdrehend a3 a4 F4 Im Fall für den gezeigten Hebel gilt daher durch Anwenden des allgemeinen Hebelgesetzes: F1 ⋅ a1 + F2 ⋅ a2 + F3 ⋅ a3 = F4 ⋅ a4 r r r r denn die Kräfte F1 , F2 und F3 bewirken eine Drehung nach links, der die Kraft F4 nach rechts entgegenwirkt. 10TG - MECHANIK 8.7 P. Rendulić 2012 HEBEL UND DREHMOMENT 58 Aufgaben 8.7.1 Schraubenschlüssel An einem Schraubenschlüssel mit dem wirksamen Hebelarm a1 = 22 cm wirkt eine Kraft F1 von 60 N. Durch Aufstecken eines Rohres wird der Hebelarm um 200 mm verlängert. Wie groß ist das Hebeldrehmoment a. des einfachen Schlüssels? b. mit dem Aufsteckrohr? 8.7.2 Güterwagen Ein Güterwagen der Eisenbahn von der Länge L = 12 m und einer Masse von 27 t ist mit dem vorderen Räderpaar entgleist und soll wieder auf die Schienen gehoben werden. Der Achsenabstand beträgt d = 8 m, der Schwerpunkt liegt in der Mitte. Welche Kraft ist am vorderen Ende des Wagens anzusetzen? 8.7.3 Unterschiedliche Hebel a. Benennen die untenstehenden Hebelarten und ermittele jeweils die erforderliche Kraft F2, damit Gleichgewicht herrscht. b. Wie ändert sich die erforderliche Kraft F2 für jeden der gezeichneten Hebel, wenn der Hebelarm L1 doppelt so lang wird? 8.7.4 Zange Eine Zange wird nach der Skizze am langen Zangenschenkel mit einer Kraft F1 = 180 N betätigt. Der Schenkel des Zangenmaules misst bis zum Drehpunkt L2 = 20 mm. Wie lang muss der Hebelarm L1 gemacht werden, wenn an der Schneide eine Kraft F2 = 1200N wirken soll? 10TG - MECHANIK P. Rendulić 2012 HEBEL UND DREHMOMENT 59 8.7.5 Mehrere angreifende Kräfte Ein einseitiger und ein zweiseitiger Hebel sind nach Skizze mit den Kräften F1 bis F4 belastet. Ermittele mithilfe des verallgemeinerten Hebelgesetzes die Kraft F3. 8.7.6 Bockgerüst Das Bockgerüst (siehe Abbildung) ist mit einem Mörtelkübel von 100 kg Masse und 25 Ziegelsteinen belastet (Masse eines Ziegelsteins: mZ = 3,5 kg). a. Welche Kraft FA wirkt auf Bock A? b. Welche Kraft FB wirkt auf Bock B? Gegeben: L1 = 80 cm, L2 = 120 cm, L3 = 60 cm