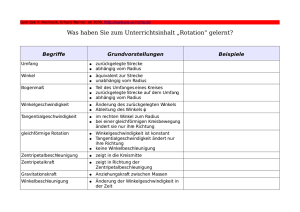
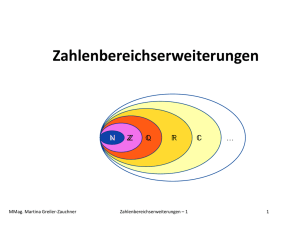
Grundvorstellungen mathematischer Inhalte

Rudolf vom Hofe
Grundvorstellungen
mathematischer Inhalte
Spektrum Akademischer Verlag Heidelberg • Berlin • Oxford
Inhalt
Einleitung: Ausgangspunkt und Ziel der
Untersuchung
1 Ursprünge des Grundvorstellungskonzepts
in der deutschen Mathematikdidaktik
1.1 Ausgangsüberlegungen 15
1.2 "Vorstellungen" bei Euler 19
1.3 Überblick 22
1.4 "Anschauungen" und "Vorstellungen" in der Ära
Pestalozzi 24
1.4.1 Pestalozzi 24
1.4.2 Herbart 27
1.4.3 Diesterweg und Hentschel 29
1.4.4 Didaktischer Fortschritt und seine Grenzen 31
1.5 "Vorstellungen" bei Kühnel 34
1.5.1 Pädagogische und psychologische Ausgangsposition 34
1.5.2 Genese mathematischer Begriffe 36
1.5.3 Zahl- und Operationsvorstellungen 38
1.5.4 Tragfähigkeit mathematischer Begriffe 40
1.5.5 Psychologische und didaktische Modellierung 41
1.5.6 Die Entwicklung nach Kühnel 42
1.6 "Anschauungen" bei Johannes Wittmann 44
1.6.1 Theoretische Ausgangsposition 44
1.6.2 Begriffsgenese und Anschauung 45
1.6.3 Ganzheitliches Rechnen 47
1.6.4 Mengenanschauungen als Grundlage der Zahl- und
Operationsbegriffe 48
1.6.5 Tragfähigkeit des Begriffes 51
1.6.6 Didaktische und psychologische Modellierung 52
1.7 "Vorstellungen" und "Verinnerlichungen" bei Piaget 54
1.7.1 Psychologie der Intelligenz 54
1.7.2 Vorstellungsbilder 56
1.7.3 Der Prozeß der Verinnerlichung 58
1.7.4 Beschreibung von Pseudokommunikation 60
1.7.5 Psychologisches Modell und didaktische
Konsequenzen 62
1.8 "Vorstellungsgrundlagen" bei Breidenbach 64
1.8.1 Theoretische Ausgangspositionen 64
1.8.2 Genese mathematischer Begriffe 66
1.8.3 Spielhandlung und Vorstellungsgrundlage 67
1.8.4 Vorstellungsgrundlage der Multiplikation 68
1.8.5 Didaktisches Modell 71
1.9 "Grundvorstellungen" bei Oehl 74
1.9.1 Herauslösen und Wiedererkennen 74
1.9.2 Grundvorstellungen und operatives Denken 76
1.9.3 Grundvorstellungen der Multiplikation 77
1.9.4 Erweiterung von Grundvorstellungen 79
1.9.5 Didaktisches Modell 81
1.10 "Grundvorstellungen" bei Griesel 83
1.10.1 Theoretische Ausgangspositionen 83
1.10.2 Zahlen und Mengen - Grundvorstellungen der
elementaren Verknüpfungen von natürlichen Zahlen 84
1.10.3 Größen und Repräsentanten - Grundvorstellungen beim
Rechnen mit Größen 87
1.10.4 Operatoren - Grundvorstellungen der Multiplikation von
Bruchzahlen 90
1.10.5 Grundvorstellungen als didaktische Kategorie 93
1.11 Zusammenfassung und Ausblick 95
1.11.1 Kontinuität und didaktischer Fortschritt 95
1.11.2 Grundvorstellungsidee 97
1.11.3 Weitere Konzepte im Bedeutungsfeld von
Grundvorstellungen 98
1.11.4 Perspektiven 100
2 Grundvorstellungen als didaktisches Modell normative, deskriptive und konstruktive Aspekte
2.1 Konflikte zwischen formalem und intuitivem Bereich 103
2.2 Individuelle Prägungen begrifflicher Strukturen und
"Subjektive Erfahrungsbereiche" 107
2.3 Vorschläge für eine konstruktive Analyse von
Schülerstrategien auf der Basis eines erweiterten
Grundvorstellungskonzepts 113
2.3.1 Erste Fallstudie: Ingo und die Temperatur 113
2.3.2 Zweite Fallstudie: Melanie und der Operator 119
2.4 Ausbilden von Grundvorstellungen 123
2.4.1 Normative Leitlinien und individuelle
Erklärungsmodelle 123
2.4.2 Grundvorstellungen und "Subjektive
Erfahrungsbereiche" 126
2.4.3 Grundvorstellungen und "fundamentale Ideen" 128
2.4.4 Ausblick 129
Schluß: Zusammenfassung und Ausblick
Literatur