8C 2

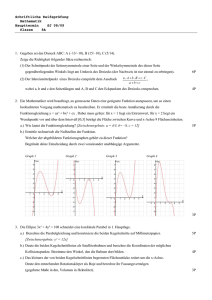
Viel Erfolg!
NAME:
8C
1
Nachtrag zur 3. SCHULARBEIT
13. 4. 2012
WAHRSCHEINLICHKEITSRECHNUNG - Karateturnier
24 P.
Ein Trainer weiß aus Erfahrung, dass seine Damen wie z. Bsp. Ulli nur mit 20 %
Wahrscheinlichkeit ihren Gegnerinnen unterliegen.
a)
Berechne die Wahrscheinlichkeit, dass Ulli von 40 Kämpfen höchstens 3 verliert.
5
b)
Unter wie vielen Kämpfen gewinnt sie mit einer Wahrscheinlichkeit von 99 % mindestens einen?
4
c)
Wie groß ist die Wahrscheinlichkeit, dass es unter den 1000 Turnieren der letzten Jahre
höchstens 275 Niederlagen für diese Damenmannschaft gab? (Skizze)
5
d)
Mit wie vielen Siegen kann der Trainer mit 95% W. bei diesen 1000 Kämpfen rechnen?
In welchem symmetrischen Intervall um  liegen diese? (Skizze)
5
e)
Beim letzten Auslandsaufenthalt hatten sie Pech: Nicht alle bekamen ein Zimmer.
Das Hotel mit 250 Betten hatte zu 4% überbucht, da 7% der Gäste erfahrungsgemäß nicht
anreisen. Mit welcher Wahrscheinlichkeit passiert es dann leider, dass mehr als
250 Personen einchecken und nicht alle ein Zimmer bekommen?
2
5
18 P.
WACHSTUMSMODELLE
Die Tabellen beschreiben das rapide Ansteigen der Jungscharkinder in Ilz und Umgebung, seit
Anita Gruppenleiterin ist.
Stelle fest, welche der Tabellen ein a) lineares, b) exponentielles oder c) ein anderes Wachstum
beschreibt. Stelle für die Fälle a) und b) die Gleichungen auf.
A
M1
B
t
N(t)
1
M2
t
N(t)
120
1
3
270
4
405
M3
t
N(t)
120
1
120
3
270
3
270
4
420
4
345
Für a) und b): (i) Wie viele Jungscharkinder gab es bei Anitas Beginn (t=0)?
8
6
(ii) Wann wird sich die Anzahl verzehnfacht haben?
C
Welches Wachstum hältst du für wahrscheinlicher: a) oder b) Wahrscheinlich wäre ein drittes Modell besser. Wie würde dieses deiner Meinung nach
verlaufen? (keine Gleichung, nur Modellbeschreibung!)
4
3
30 P.
DIFFERENTIAL- UND INTEGRALRECHNUNG
2
Gegeben ist der Graph der Funktion f mit f(x ) = 4x ex
Begründe, woran man erkennen kann, dass f1 der Graph dieser Funktion sein muss.
a)
f1
f2
4
f3
f4
b)
Gib je eine mögliche Funktionsgleichung für die restlichen Graphen an.
4
c)
Welche Symmetrieeigenschaft tritt beim Graphen f1 auf?
 symm.bez. der x-Achse
 symm. bez. der y-Achse
2
 symm. bez. (0/0)
d)
Begründe, warum N(0/0) einzige Nullstelle dieser Funktion ist.
Die Funktion ist im Nullpunkt streng monoton fallend.
In welchem Bereich ist der Graph streng monoton fallend? Bestimme diese Punkte exakt.
e)
Uneigentliches Integral:
Zeige, dass der Graph mit der x-Achse eine endliche Fläche einschließt.
f)
8
6
Aus der Physik: Im Gravitationsfeld der Erde wird ein Raumschiff von der Umlaufbahn im
Abstand r1 vom Erdmittelpunkt auf die Umlaufbahn im Abstand r2 vom Erdmittelpunkt gehoben.
r2

Für die dafür notwendige Arbeit W gilt: W  F(r) dr .
r1
F(r) ist die auf das Raumschiff wirkende Gravitationskraft.
 Kreuze jene Aussagen über diese Arbeit W an, die richtig sind.
 Die Arbeit ist das Produkt aus aufgewendeter Kraft mal zurückgelegtem Weg.
 Die Arbeit kann als Summe vieler Teilarbeiten gesehen werden.
Dabei wird angenommen, dass die Kraft innerhalb sehr kleiner
Wegstücke jeweils konstant bleibt.
 Bewegt sich das Raumschiff in konstanter Höhe r1, ist die Arbeit null.
 Die Arbeit lässt sich mit F(r2) – F(r1) berechnen.
 Die Arbeit entspricht zahlenmäßig dem Flächeninhalt jener Fläche, die die
Funktion F(r) im Intervall [r1, r2] mit der r- Achse einschließt.
6
Viel Erfolg!
NAME:
4
14 P.
ANALYTISCHE GEOMETRIE
E1: 6x + 3y + 2z = 11 E2: X = (6/2/2) + t(-1/2/0) + s(-2/2/3)
a)
Zeige auf zwei verschiedene Arten, dass die Ebenen E1 und E2 disjunkt parallel sind.
5
b)
Berechne ihren Normalabstand.
3
c)
Gib die Gleichung jener Kugel an, die E1 und E2 als Tangentialebenen hat und E1 in T(1/1/1)
3
berührt.
d)
Begründe, warum die Gerade g: X = (1/2/3) + m(1/2/-6) parallel zu E1 ist.
5
SPAREN UND KREDITE
a)
Kosi weiß noch nichts davon, aber eine gute Fee hat seit ihrer Geburt zu Beginn jedes Monats
100 € auf ein mit 4% verzinstes Sparbuch eingezahlt.
Diese inzwischen beträchtliche Summe wird ihr zur bestandenen Matura ausbezahlt werden 
Wie viel wird das sein? (Rechne mit peff und der Einfachheit halber mit 18 Jahren!)
b)
3
14 P.
Umgekehrter Fall:
Jemand nimmt einen Kredit über 30 000 € zu 6% Jahreszinssatz auf und will ihn innerhalb von 10
Jahren durch monatliche Tilgung abbezahlen. Wie hoch ist eine Monatsrate?
Wie hoch ist die offene Restschuld nach 5 Jahren Laufzeit bei monatlicher Rückzahlung?
(Ersatzlösung: R= 340 €)
4
5
5
100 P.
1
92 - 100
2
79 - 91
3
62 - 78
4
50 - 61
5
0 - 49