Heidelberger Taschenbücher Band 56

Heidelberger Taschenbücher Band 56
M. J. Beckmann . H. P. Künzi
Mathematik für Ökonomen I
Mit 103 Abbildungen
Springer-Verlag Berlin Heidelberg New York 1969
Prof. Dr. M. J.
BECKMANN
Institut für Ökonometrie und Unternehmensforschung
der Universität Bonn
Prof. Dr. H. P.
KÜNZI
Institut für Operations Research und elektronische Datenverarbeitung
der Universität Zürich
ISBN 978-3-540-04551-9
ISBN 978-3-662-00504-0 (eBook)
DOI 10.1007/978-3-662-00504-0
Alle Rechte vorbehalten.
Kein Teil dieses Buches darf ohne schriftliche Genehmigung des Springer- Verlages übersetzt oder in irgendeiner Form vervielfaltigt werden.
Library of Congress
© by Springer-Verlag Berlin· Heidelberg 1969.
Catalog Card Number 79-83679
Titel-Nr.7586
G. B. und M. K.
gewidmet
Vorwort
Die mathematischen Methoden, die in der Ökonomie und
Unternehmensforschung verwendet werden, ändern und erweitern
sich beständig. Die Analysis (Differential- und Integralrechnung)
gehört aber zu dem Grundstock der mathematischen Hilfsmittel,
deren jeder Wirtschaftswissenschaftler bedarf, um schon so einfache Begriffe wie Elastizität der Nachfrage, spezielle Produktionsfunktionen, Stabilität des Gleichgewichts etc. anwenden zu
können. Die Analysis ist auch nicht durch die Möglichkeit überholt worden, die Preistheorie auf ganz anderem Fundament aufzubauen wie der Punkt-Mengenlehre bei DEBREU 1 . Für alle Fragen
der ökonomischen Dynamik, also auch der Wachstumstheorie, ist
die Analysis auch heute noch unentbehrlich.
In diesem einleitenden Band wird versucht, die relevanten Teile
der Analysis im Hinblick auf ökonomische Anwendungen zu entwickeln. Dabei beschränken wir uns zunächst auf die Analysis in
einer Variablen. In einem zweiten Bande sollen die Funktionen
mehrere Variablen und ihre Anwendungen in der Wirtschaftswissenschaft behandelt werden. Im dritten Band wird die lineare
Algebra, soweit sie den Ökonomen interessiert, dargestellt.
Diese drei Bände sind als Lehrbücher für einführende Vorlesungen in die Mathematik für Ökonomen und Unternehmensforscher gedacht, zugleich auch als Nachschlagebücher über die
wichtigsten mathematischen Hilfsmittel des Wirtschaftswissenschaftlers. Auch können die hier entwickelten ökonomischen Beispiele dienen, Mathematikern einen ersten Überblick über die
Anwendungsmöglichkeiten der Mathematik auf dem Gebiet der
Wirtschaftswissenschaften zu bieten.
Bei der Einteilung des Stoffes und in der mathematischen Darlegung haben wir uns in verschiedenen Kapiteln durch die pädagogisch hervorragenden Vorlesungsnachschriften von Prof. Dr.
WALTER SAXER, Honorarprofessor der Eidg. Techn. Hochschule
Zürich, leiten lassen, dem an dieser Stelle für seine freundliche
Genehmigung dazu herzlichst gedankt sei. Den Herren Prof. Dr.
1 DEBREU, G., Theory of Value. An Axiomatic Analysis of Economic
Equilibrium, New York 1965.
VII
G. HAUSER, Prof. Dr. R. HENN und Dr. K. PETERS vom SpringerVerlag danken wir für die zahlreichen Anregungen.
Bei der Redaktion des vorliegenden ersten Bandes haben sich
die beiden Herren Dr. E. BLUM und R. LANDTWING besonders
verdient gemacht. Ihnen verdanken wir auch verschiedene Verbesserungsvorschläge.
Dem großen Interesse und Entgegenkommen des Springer-Verlages bei der Herausgabe dieses Werkes gebührt ebenfalls aufrichtiger Dank.
Wir glauben, daß wir mit der projektierten Reihe eine Lücke
in der deutschsprachigen Literatur ausfüllen können. Für Vorschläge aus dem Kreis der Leser zu Verbesserungen oder Erweiterungen sind wir jederzeit dankbar.
MARTIN J. BECKMANN und HANS P. KÜNZI
VIII
Inhaltsverzeichnis
1. Mengen, Zahlen und Funktionen
1
1.1 Mengen . . . . . . .
1.1.1 Der Mengenbegriff
1.1.2 Definitionen .
1
1
1
1.2 Zahlen. . . . . . . . .
1.2.1 Einleitung. . . . . . . . . . .
1.2.2 Über das System der reellen Zahlen
1.2.3 Einiges über Ungleichungen und den absoluten
Betrag . . . . . . . . . . . . .
a) Ungleichungen . . . . . . . .
b) Intervalle. . . . . . . . . . .
c) Vorzeichen und absoluter Betrag .
1.2.4 Beschränkte Zahlenmengen . . . .
1.2.5 Zahlen und Größen in der Ökonomie
2
2
3
1.3 Funktionen. . . . . . . .
1.3.1 Der Funktionsbegriff .
1.3.2 Graphische Darstellung
1.3.3 Die elementaren Funktionen .
a) Die rationalen Funktionen
b) Algebraische Funktionen .
c) Die trigonometrischen Funktionen
d) Die Exponentialfunktion und die Logarithmusfunktion . . . . . . . . . . . . . .
1.3.4 Folgen (Funktionen mit ganzzahligen Veränderlichen) . . . . . . . . . . . . .
10
10
12
17
17
17
18
20
1.4 Funktionen in der Wirtschaftswissenschaft
1.4.1 Die Nachfragefunktionen
1.4.2 Produktionsfunktionen
1.4.3 Kostenfunktionen . .
1.4.4 Die Angebotsfunktion .
1.4.5 Die Konsumfunktion .
1.4.6 Die Investitionsfunktion .
1.4.7 Die aggregierte Produktionsfunktion
1.4:8 Die aggregierte Angebotsfunktion . .
1.4.9 Die Nachfrage nach Transaktionskasse
22
22
24
26
27
28
29
29
29
30
5
5
6
6
7
8
18
IX
1.4.10 Die Liquiditätspräferenzfunktion (Liquidity pre30
ference) . . . . . . . . . .
1.5 Grenzwerte von Zahlenfolgen . . . . . . . . .
1.5.1 Die beschränkten Zahlenfolgen. . . . . .
1.5.2 Definition des Häufungspunktes einer Folge
1.5.3 Monotone und konvergente Zahlenfolgen
1.5.4 Die Zahl e. . . . . . . . .
1.5.5 Das Rechnen mit Grenzwerten
31
31
31
32
33
35
1.6 Grenzwerte von Funktionen.
37
1.7 Stetige Funktionen. . . . .
1.7.1 Definition der Stetigkeit
1.7.2 Eigenschaften stetiger Funktionen.
1.7.3 Die Stetigkeit ökonomischer Funktionen
41
41
1.8 Anhang zum 1. Kapitel. . .
1.8.1 Die Polarkoordinaten .
1.8.2 Kurvenscharen . . . .
1.8.3 Die komplexen Zahlen
.
Der Begriff der komplexen Zahl.
1.8.4 Das Rechnen mit komplexen Zahlen.
a) Addition und Subtraktion.
b) Multiplikation.
c) Division . . .
d) Das Potenzieren
e) Das Radizieren
50
50
51
53
54
55
55
56
56
57
58
2. Differentialrechnung.
2.1 Einleitung
. . .
44
48
60
60
2.2 Der Differentialquotient
60
2.2.1 Definition des Differentialquotienten
60
2.2.2 Stetigkeit und Differenzierbarkeit einer Funktion 62
2.2.3 Ein physikalisches Beispiel. . . . . . . . . . 63
2.2.4 Ein ökonomisches Beispiel. . . . . . . . . . 64
2.2.5 Direkte Berechnung der ersten Ableitung. . . . 65
2.2.6 Ökonomische Begriffe, die auf Ableitungen beruhen. . . . . . . . . . . . . . . . . . . 65
2.3 Differentiationsregeln . . . . . . . . . . . . . .
2.3.1 Die Differentiation der Funktionenfix)=c=const.
undg(x)=x . . . . . . . . . . . . . . . .
2.3.2 Die Differentiation der Summe zweier Funktionen
x
66
66
67
2.3.3 Die Differentiation eines Produktes zweier Funktionen. . . . . . . . . . . . . . . . . . .
2.3.4 Die Differentiation der Potenzfunktionf(x)=x".
2.3.5 Die Differentiation des Quotienten zweier Funktionen. . . . . . . . . . . . . . . . . . .
2.3.6 Die Differentiation der inversen Funktion . . .
2.3.7 Die Kettenregel oder die Differentiation von zusammengesetzten Funktionen. . . . . . . . .
67
69
70
71
73
2.4 Die Exponentialfunktion und die Logarithmusfunktion
2.4.1 Eigenschaften der Exponentialfunktion . . . .
2.4.2 Eigenschaften der Logarithmusfunktion . . . .
2.4.3 Beziehungen zwischen Logarithmusfunktionen mit
verschiedener Basis . . . . . . . . . . . .
2.4.4 Die Differentiation der Logarithmusfunktion .
2.4.5 Die Differentiation der Exponentialfunktion
76
76
76
2.5 Wachstumsraten. . . . . . . . . . . . .
2.5.1 Stetiges Wachstum mit konstanter Rate . .
2.5.2 Zins und Zinseszins. . . . . . . . . . .
79
79
81
77
78
79
2.6 Die logarithmische Ableitung und die Elastizität einer
Funktion. . . . . . . . . . . . .
83
2.6.1 Die logarithmische Darstellung. .
83
2.6.2 Die logarithmische Ableitung. . . . . . . . . 84
2.6.3 Die Elastizität einer Funktion . . . . . . . . 86
2.6.4 Die Preiselastizität der Nachfrage. . . . . . . 88
2.6.5 Die Elastizität anderer ökonomischer Funktionen 91
2.7 Die trigonometrischen Funktionen. . . . . . . . .
2.7.1 Zusammenstellung einiger wich tiger Eigenschaften
der trigonometrischen Funktionen . . . . . .
2.7.2 Die Differentiation der trigonometrischen Funktionen. . . . . . . . . . . . . . . . .
92
92
93
2.8 Die zyklometrischen Funktionen. . . . . . . . . .
2.8.1 Der Begriff der zyklometrischen Funktionen . .
2.8.2 Die Differentiation der zyklometrischen Funktionen. . . . . . .
95
95
2.9 Hyperbolische Funktionen .
99
2.10 Der Mittelwertsatz der Differentialrechnung
2.10.1 Der Satz von Rolle. .
2.10.2 Der Mittelwertsatz . .
2.10.3 Monotone Funktionen
98
101
101
102
103
XI
2.11 Das Differential . . . . . . . . . . . . .
2.11.1 Der Begriff des Differentials. . . . . .
2.11.2 Regeln für die Bildung des Differentials.
2.11.3 Eine Anwendung des Differentials auf die Fehlerrechnung. . . . . . . . . . . .
2.12 Höhere Ableitungen. . . . . . . . . .
2.12.1 Der Begriff der höheren Ableitungen
2.12.2 Die n-te Ableitung eines Produktes.
2.12.3 Ein physikalisches Beispiel . . . .
2.12.4 Ökonomische Beispiele . . . . . .
2.13 Konvexe und konkave Funktionen . . .
2.13.1 Der Begriff der konvexen Funktion.
2.13.2 Eigenschaften konvexer Funktionen
Der Stützgeradensatz für konvexe Funktionen
. ..... .
2.13.3 Konvexe Bereiche . . . .
2.13.4 Konkave, quasikonkave und quasikonvexe
Funktionen. . . . . .
2.13.5 Ökonomische Beispiele .
3. Diskussion von Funktionen. . .
104
104
106
107
107
107
108
108
109
111
111
112
113
114
114
115
117
3.1 Allgemeine Kurvendiskussion
3.1.1 Erste Stufe. . . . . .
3.1.2 Zweite Stufe. . . . .
a) Das lokale Verhalten einer Funktion
b) Eine globale Eigenschaft . . . . .
3.1.3 Dritte Stufe . . . . . . . . . . . .
3.1.4 Ein Beispiel . . . . . . . . . . . .
3.1.5 Mathematische Beispiele zur Optimierung
120
120
122
122
125
127
3.2 Ökonomische Beispiele zur Optimierung . . .
3.2.1 Gewinnmaximierung . . . . . . . . . . .
3.2.2 Die optimale Einsatzmenge in der Produktion.
3.2.3 Stückkostenminimierung . . . .
129
129
132
133
3.3 Spezielle Funktionen in der Ökonomie .
3.3.1 Engel-Funktionen . . . . . . .
3.3.2 Produktionsfunktionen . . . . .
a) Die lineare Produktionsfunktion
.
b) Die Cobb-Douglas-Produktionsfunktion
c) Die gebrochene rationale Produktionsfunktion
d) CES-Produktionsfunktion. . . . . . . . .
135
135
138
139
140
141
142
XII
117
117
4. Die Integralrechnung
. . . . . . . .
146
4.1 Der Begriff des bestimmten Integrals
4.1.1 Einleitung. . . . . . . . .
4.1.2 Die Definition des bestimmten Integrals
4.1.3 Sätze über das bestimmte Integral.
146
146
148
151
4.2 Mittelwertsätze der Integralrechnung. . . .
153
4.3 Das unbestimmte Integral. . . . . . . . .
4.3.1 Der Begriff des unbestimmten Integrals
4.3.2 Zusammenstellung unbestimmter Integrale .
155
155
155
4.4 Der Hauptsatz der Integralrechnung . . . . . .
156
4.5 Die Substitutionsmethode . . . . . . . . . . .
158
4.5.1 Die Substitutionsmethode für unbestimmte Integrale . . . . . . . . . . . . . . . . . . . 158
4.5.2 Die Substitutionsmethode für bestimmte Integrale 162
4.6 Die Methode der partiellen Integration . .
165
4.7 Die Integration rationaler Funktionen . .
4.7.1 Eigenschaften rationaler Funktionen.
4.7.2 Partia1bruchzerlegung rationaler Funktionen
4.7.3 Die Integration der rationalen Funktionen .
167
167
168
172
4.8 Uneigentliche Integrale. . . . . . . . . . . .
4.8.1 Die Integration von Funktionen mit SprungsteIlen
4.8.2 Die Integration von Funktionen mit Polen . . .
4.8.3 Unendliche Integrationsintervalle . . . . . . .
176
176
177
178
4.9 Einige ökonomische Anwendungen der Integralrechnung. . . . . . . . . . . . . .
4.9.1 Kapitalisierung. . . . . . .
4.9.2 Konstante Abschreibungsrate.
4.9.3 Interner Zinssatz . . . . . .
4.9.4 Der Produktpreis bei räumlichem Marktgleichgewicht . . . . . . . .
4.9.5 Die Konsumentenrente . . . . . . . . . . .
a) Lineare Nachfrage. . . . . . . . . . . .
b) Nachfragefunktion mit konstanter Elastizität.
180
180
182
182
183
184
185
185
5. Reihen. . . . . . . . . . .
187
5.1 Begriffe und Definitionen.
187
5.2 Reihen mit positiven Gliedern.
5.2.1 Das Wurzelkriterium . .
191
192
XIII
5.2.2 Das Quotientenkriterium . .
5.2.3 Kriterien für die Divergenz. .
193
193
5.3 Absolute und bedingte Konvergenz.
194
5.4 Ökonomische Beispiele. . . . . .
5.4.1 Der Multiplikatoreffekt bei einmaliger Investition. . . . . . . . . . . . . . . . . . . .
5.4.2 Der Multiplikatoreffekt bei andauernder Investition. . . . . . . . . . . . . . . . .
5.4.3 Zinseszins . . . . . . . . . . . . . .
5.4.4 Der Kapitalwert eines Einkommenstromes
5.4.5 Annuitäten . . . .
195
5.5 Gleichmäßige Konvergenz
196
196
196
197
198
. . . . . . . .
198
5.6 Potenzreihen . . . . . . . . . . . . . .
199
5.7 Taylorsche Formeln und Taylorsche Reihen.
203
5.8 Die Berührung von Kurven und ein Kriterium für Extremalstellen . . . . . . . . . . . . . . . . . . .
209
5.9 Unbestimmte Ausdrücke (die L'Hospitalsche Regel)
Namen- und Sachverzeichnis
XIV
. . . . . . . . . . . ..
212
219
Mathematik rur Ökonomen I
1. Mengen, Zahlen und Funktionen
1.1 Mengen
1.1.1 Der Mengenbegriff
Der Begriff der Menge ist grundlegend für die ganze Mathematik. Wir können eine Menge als "die Zusammenfassung von wohlbestimmten und wohlunterschiedenen Dingen zu einem Ganzen"
definieren. Diese Dinge werden Elemente der Menge genannt. Ist
A eine Menge, so schreiben wir für die Aussage, a sei ein Element
von A (a sei in A enthalten) symbolisch: aEA. Das Symbol a$A
bedeutet: a ist nicht in A enthalten.
Wir geben einige Beispiele von Mengen, wie sie im folgenden
immer wieder auftreten, an:
1. Die Menge N der natürlichen Zahlen. Es gilt dann etwa:
lEN, 5EN, ±$N.
2. Die Menge G der geraden natürlichen Zahlen. Es gilt zum
Beispiel: 2EG, 3$G.
3. Die Menge U der ungeraden natürlichen Zahlen.
4. Die Menge C, die aus den Elementen 1, 2, 5 und 7 besteht.
Wir schreiben dafür: C={l,2,5,7}.
5. Der Einheitskreis K ist die Menge der Punkte P=(x,y),
deren Koordinaten die Gleichung x 2 + y2 = 1 erfüllen. Man schreibt
dafür abkürzend: K = {P=(x,y) I x 2 + y2 = l}.
6. Die Menge, die kein Element enthält, die leere Menge, bezeichnen wir mit dem Symbol(/).
1.1.2 Definitionen
Die Menge A heißt Teilmenge von B, wenn für jedes aEA gilt:
aEB. Wir schreiben dafür Ac BI oder B:::J A. Gibt es ein bEB,
so, daß b$A, so heißt A eine echte Teilmenge von B.
Das Symbol A q: B bedeutet: A ist nicht Teilmenge von B. Ist
A c Bund B cA, so heißen die beiden Mengen gleich: A = B.
1
I
Lies: Die Menge A ist enthalten in der Menge B.
BeckmannjKünzi I
Für die oben definierten Mengen N, G, U, C gelten die Beziehungen:
GeN;
C c N;
U c N, G<t U, C<t G.
Ist Ac B; so heißt die Menge der Elemente bEB, die nicht zu A
gehören, die Komplementärmenge von A in B, in Zeichen: B - A.
Es gilt zum Beispiel G = N - U.
Die Menge der Elemente, die sowohl in A als auch in B liegen,
bezeichnen wir mit An B und nennen sie den Durchschnitt von
A und B. Man sagt auch, A werde mit B geschnitten (vgl. Abb. 1).
Die Menge der Elemente, die mindestens in einer der beiden
Mengen A und B enthalten sind, heißt die Vereinigung von A und B.
Man bezeichnet sie mit dem Symbol: Au B (A vereinigt mit B)
(vgl. Abb. 2).
Es gelten zum Beispiel die folgenden Beziehungen:
GnN=G;
GnU=(/J;
CnG={2}.
Um zu zeigen, daß zwei Mengen A und B gleich sind, weist man gewöhnlich nach, daß sowohl A c B als auch B c A ist.
Auf diese Weise lassen sich leicht die folgenden Regeln beweisen:
Au (Bu C)=(Au B)u C,
An (B n C) = (A n B) n C,
An (Bu C)=(A n B)u (A n C),
Au (Bn C)=(A u B)n(A u C).
Abb,2
Abb. I
1.2 Zahlen
1.2.1 Einleitung
Die mathematischen Methoden der Wirtschaftswissenschaften
gehen aus vom Operieren mit Zahlen und Größen wie Absatz und
Preis. Die Zahlen bilden auch das Fundament der Analysis. Es
kann nicht unsere Aufgabe sein, in erkenntnistheoretischer Weise
die Grundlagen des Zahl begriffs zu erörtern. Diese Aufgabe soll
2
dem Mathematiker oder noch eher dem Philosophen überlassen
bleiben 1. Uns kommt es vor allem darauf an, mit den gegebenen
Zahlen richtig zu operieren unter Verwendung bestimmter Gesetze.
1.2.2 Über das System der reellen Zahlen
Die natürlichen Zahlen 1,2,3, ... entstehen durch die Operation
des Abzählens. Sie können ohne Einschränkung addiert und multipliziert werden. Um auch Gleichungen der Form a+x=b, wobei
a und b beliebige, gegebene natürliche Zahlen sind, allgemein lösen
zu können, muß die Menge der natürlichen Zahlen durch Hinzunahme der Null und der negativen Zahlen -1, -2, -3, ... zur
Menge der ganzen Zahlen erweitert werden. Die Gleichung a + x = b
ist auch dann immer eindeutig lösbar, wenn a und b beliebige ganze
Zahlen sind, oder anders ausgedrückt: Die Subtraktion läßt sich im
Bereich der ganzen Zahlen unbeschränkt durchführen.
p und q seien beliebige ganze Zahlen. Erweitert man die Menge
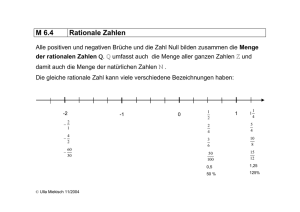
der ganzen Zahlen durch Einführen der rationalen Zahlen
E,
q
q =1= 0, so besitzt jede Gleichung der Form a x = b (zum Beispiel
2 x = 3), wobei a =1= 0 und b beliebige rationale Zahlen sind, eine
eindeutig bestimmte rationale Lösung. Die Umkehroperation der
Multiplikation, die Division, ist also in der Menge der rationalen
Zahlen allgemein definiert.
Es ist zweckmäßig und üblich, die rationalen Zahlen anschaulich
durch Punkte einer geraden Linie, der Zahlengeraden, darzustellen,
indem man auf dieser Geraden einen beliebigen Punkt als den Nullpunkt festsetzt, einen andern als Punkt 1. Die Strecke zwischen 0 und I
dient dann als Maßstab, um jeder positiven oder negativen rationalen Zahl eine bestimmte Stelle auf der Zahlengeraden zuzuordnen.
Es ist üblich, die positiven Zahlen rechts von 0 und die negativen
links davon anzuordnen.
!
!
-3 -2
! !
-1
0
!
j
2
3
Abb.3
Denkt man sich auf obige Weise die rationalen Zahlen auf der
Zahlengeraden dargestellt, so haben diese die Eigenschaft, daß sie
1 R. DEDEKIND, Was sind und was sollen die Zahlen. 4. Auflage. Braunschweig 1918.
H. WEYL, Philosophie der Mathematik und Naturwissenschaft. München
1927.
I"
3
die Gerade "überall dicht" belegen. Das besagt, daß es zwischen zwei
beliebig nahe aneinanderliegenden rationalen Zahlen immer noch
weitere rationale Zahlen gibt. So liegt zwischen 0 und /0 sicher
noch die rationale Zahl 150' Zwischen 0 und 150 liegt die rationale
Zahl 10100 usw.
Stellt man die rationalen Zahlen, wie oben beschrieben, durch
Punkte der Zahlengeraden dar, so stellt man fest, daß der Bereich der
rationalen Zahlen abermals auf natürliche Weise erweitert werden
kann, indem man jedem Punkt der Zahlengeraden eine Zahl zuordnet. Durch diese eindeutige Zuordnung wird der Bereich der rationalen Zahlen auf den Bereich der reellen Zahlen erweitert. Beispielsweise
keine
entspricht der geometrisch wohldefinierten Strecke
rationale Zahl. Das gleiche gilt für den Umfang n eines Kreises mit
dem Radius t. Reelle Zahlen, die nicht rational sind, nennt man
irrationale Zahlen. Die irrationalen Zahlen liegen wie die rationalen
Zahlen überall dicht auf der Zahlengeraden.
Man kann zeigen, daß sich jede irrationale Zahl beliebig genau
durch rationale Zahlen approximieren läßt. Jede reelle Zahl läßt
sich nämlich durch einen Dezimalbruch darstellen. Abbrechende
und periodische Dezimalbrüche entsprechen dabei rationalen Zahlen, die übrigen den irrationalen Zahlen. Jeder nichtabbrechende
Dezimalbruch läßt sich aber durch abbrechende Dezimalbrüche
beliebig gut annähern.
läßt sich zum Beispiel von unten her
Die irrationale Zahl
durch kleinere rationale Zahlen und von oben her durch größere
rationale Zahlen beliebig gut approximieren.
Wir verzichten hier auf einen allgemeinen Beweis, geben aber
einige Approximationsschritte an.
z~ = 1 <0<z'{ =2,
da 1 <2<4;
z~=1,4<0<z;=1,5,
da (l,4)2<2<(l,W;
z~ = 1,41 <0 <z'~ = 1,42, da (1,41)2 <2< (1,42)2. 1
Die Zahlen z; und z;' bestimmen eine Zahlen strecke, ein Intervall
h Man sieht, daß jedes Intervall I i + 1 ganz im vorangehenden
Intervall I i enthalten ist. Die Länge der Intervalle I i strebt mit
wachsendem Index i gegen Null. Eine solche Intervallfolge
I 1,I2, ... ,Ii,'" nennt man eine Intervallschachtelung. Die Intervalle ziehen sich immer mehr auf einen bestimmten Punkt Z zusammen, der allen Intervallen zugleich angehört. Dieser innerste
Punkt Z erscheint einerseits als Grenzpunkt der aufsteigenden Folge
rationaler Punkte Z'l, z~, z~, ... , z~, ... , andererseits als Grenzpunkt
V2
0
1 Das Symbol a < b bedeutet: a ist kleiner als b. Ist mindestens eine der
Beziehungen a<b, a=b erfüllt, so schreibt man dafür a:::;;b.
4
der absteigenden Folge rationaler Punkte z'~, z;, z;, .... Der Punkt Z
ist somit gemeinsamer Grenzpunkt zweier rationaler Punktfolgen.
Man schreibt dafür:
lim z~ = !im z~ . 1
Da für jedes i gilt: z; <
n~
0
n- 00
00
< z~, folgt daraus:
lim z~ = lim z~ =
n-+oo
n-w
0.
0
Die oben beschriebene Approximation der irrationalen Zahl
durch rationale Zahlen führt uns zur folgenden analytischen Definition der reellen Zahlen: Ist Z der Grenzpunkt einer Intervallschachtelung mit rationalen Endpunkten, so nennen wir Zeine
reelle Zahl.
Von entscheidender Wichtigkeit ist die Tatsache, daß in der
erweiterten Menge der reellen Zahlen alle wesentlichen Rechengesetze der rationalen Zahlen weiterhin gelten.
1.2.3 Einiges über Ungleichungen und den absoluten Betrag
a) Ungleichungen
Zwischen zwei reellen Zahlen a und b besteht immer eine und
nur eine der drei Größenbeziehungen: a kleiner b, a gleich b oder
a größer b. Abgekürzt schreibt man dafür a < b, a = b, a> b (bzw.
b<a).
Ist entweder die erste oder die zweite Relation erfüllt, so schreiben
wir dafür:
a~b
(bzw. b'2:a).
Für das Rechnen mit Ungleichungen gelten die folgenden
Regeln:
1. Aus a~b und b~c folgt a~c.
2. Aus a~b und c~d folgt a+c~b+d.
a
b
3. Aus a~b und c>O folgt: ca~cb; - ~ -.
c
c
a
b
4. Aus a~ bund c <0 folgt: ca'2:cb; - '2: -.
c
c
5. Aus a~b folgt -a'2: -b.
I
I
6. Aus O<a~b folgt 0<
7. Aus
1
a~b<O
folgt
I
b ~ ~.
I
b ~ ~ < O.
Vgl. Abschn. 1.5.3.
5
b) Intervalle
Unter einem Intervall verstehen wir die Menge aller reellen
Zahlen x, welche eine der folgenden doppelten Ungleichungen erfüllen:
a ::; x ::; b,
a< x < b,
a::; x < b,
a < x::; b.
Man unterscheidet die folgenden Typen von Intervallen:
a::;x:S;b: Endliches abgeschlossenes Intervall (die Endpunkte x=a
und x = b gehören zum Intervall).
a < x < b: Endliches offenes Intervall (die Endpunkte gehören nicht
zum Intervall).
a:S; x < b: Endliches halboffenes Intervall.
a<x<co: }
- co < x:s; b: Unendliche Intervalle!.
-co<x<oo:
c) Vorzeichen und absoluter Betrag
Das Vorzeichen einer reellen Zahl x, das wir mit sign x bezeichnen, ist wie folgt definiert:
signx= +1
signx= -1
°
für
für
x>o,
x<O.
Für x = ist sign x nicht definiert.
Der absolute Betrag Ix I einer reellen Zahl x ist wie folgt definiert:
Ixl=x
Ixl= -x
falls
falls
x~O
ist,
x<o ist.
Es gilt zum Beispiel:
171=7
1-71=7,
101=0.
Jede reelle Zahl läßt sich also wie folgt darstellen:
x = sign x Ix!Für das Rechnen mit absoluten Beträgen seien einige Regeln angegeben, die man leicht verifizieren kann:
1. l-xl=lxl
2. Aus lxi = a, wobei a >
ist, folgt entweder x = a oder
x = - a. Ix 1= a ist gleich bedeutend mit der Gleichung x 2 = a2 •
°
1
6
Das Symbol
00
bezeichnet die "unendlich große Zahl".
3. Für beliebige reelle Zahlen x und Y gelten die sogenannten
Dreiecksungleichungen
Ix+yl::; Ixl+lyl;
Ix+ YI~llxl-IYII;
Es gilt zum Beispiel:
Ix-yl::; Ixl+lyl,
Ix - Yl ~ Ilxl-IYII·
110-31=7 <1101 +1-31 = 13,
1-3 -81= 11 >5= 11-31-1-811.
a
4. Für das Produkt ab und den Quotienten - zweier beliebiger
reeller Zahlen a und b, h '*' 0, gilt:
b
labl = lallbi,
lil= : :.
1.2.4 Beschränkte Zahlenmengen
Eine Menge A von reellen Zahlen heißt nach oben (bzw. nach
unten) beschränkt, wenn es eine reelle Zahl M gibt, so, daß x::; M
(bzw. x ~ M) ist für jedes XE A.
M heißt eine obere (bzw. untere) Schranke von A.
Ist eine Menge B gleichzeitig nach oben und nach unten beschränkt, so sagen wir, B sei beschränkt. Es gibt dann eine positive
reelle Zahl N so, daß für jedes XE B gilt: Ix I::; N. Wir nennen N
eine Schranke von B.
Das Intervall a::; x::; b ist zum Beispiel beschränkt. a und a - 1
sind untere Schranken des Intervalls, während bund b + 2 obere
Schranken sind. Die Menge der natürlichen Zahlen ist nach unten,
aber nicht nach oben beschränkt.
Die folgenden Sätze über beschränkte Mengen sind von großer
Bedeutung für den Aufbau der Differentialrechnung.
Satz 1: Ist A eine nach oben (bzw. nach unten) beschränkte
Menge von reellen Zahlen, so gibt es unter allen oberen (bzw. unteren) Schranken von A eine kleinste (bzw. größte) obere (bzw. untere)
Schranke.
Die kleinste obere Schranke von A nennt man auch die obere
Grenze oder das Supremum von A und bezeichnet sie mit sup x.
XEA
Die größte untere Schranke von A heißt untere Grenze oder das
Infimum von A und wird mit inf x bezeichnet.
XEA
7