Addition und Subtraktion von Brüchen - matheguru.one

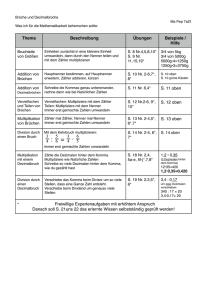
Textscript zum Aufgabenvideo „Addition und Subtraktion von Brüchen“ - Seite 1 von 4
Folie 1
Willkommen zu einem Aufgabenvideo von matheguru.one.
Folie 2
In diesem addiere und subtrahiere ich Brüche und gemischte Zahlen. Ich
erläutere dir auch Arten von Brüchen, so den echten Bruch, den unechten
Bruch und den Scheinbruch. Ich zeige dir, wie man unechte Brüche in
gemischte Zahlen umwandelt und umgekehrt, wie man Brüche erweitert und
kürzt, wie man das kleinste gemeinsame Vielfache und den größten
gemeinsam Teiler bildet, zum Beispiel auch mit der Primfaktorenzerlegung.
Folie 3
Ich habe die Nummer 6 f auf der Seite 47 der Allgemeinen Ausgabe des
Schnittpunkt-Buches für die Klasse 6 ausgewählt. Der Aufgabentext lautet:
Wandle das Ergebnis der Rechnung wenn möglich in die gemischte
Schreibweise um oder kürze. Die Aufgaben lauten 21 Zwanzigstel plus 15
Sechzehntel, 2 2 Neuntel plus ein 11 Fünfzehntel und ein 24
Fünfundzwanzigstel minus 19 Zwanzigstel.
Folie 4
Zunächst erläutere ich dir die verschiedenen Arten von Brüchen. Beim echten
Bruch ist der Zähler kleiner als der Nenner und der Bruchwert kleiner als 1,
hier rund 0,67. Beim unechten Bruch ist der Zähler größer als der Nenner, der
Bruchwert ist größer als 1, hier 2,6 und beim Scheinbruch ist der Zähler ein
Vielfaches des Nenners und der Bruchwert ist eine natürliche Zahl, hier 3.
Jetzt zeige ich dir, wie man unechte Brüche in gemischte Zahlen umwandelt
und umgekehrt. Der Bruch 13 Fünftel soll in eine gemischte Zahl umgewandelt
werden. Eine gemischte Zahl ist die Summe aus einer ganzen Zahl und einem
Bruchteil. Ich frage mich, wie oft die 5 ganz in die 13 passt. Das ist 2 mal;
dann, wie groß der Rest ist. Das ist hier 3, weil 2 Ganze sind 10 Fünftel, es
bleiben 3 Fünftel übrig und zum Schluss, wie der alte Nenner heißt. Das ist 5.
Dies ist auch den neue Nenner im Bruch. Somit sind 13 Fünftel 2 3 Fünftel. Ich
kann dies auch an der Geteiltaufgabe 13 geteilt durch 5 zeigen. Das Ergebnis
ist 2 Rest 3.
Jetzt zur Umwandlung einer gemischten Zahl in einen unechten Bruch. Zuerst
multipliziere ich die ganze Zahl mit dem Nenner des Bruchteils, also 2 mal 5,
das ergibt 10. Dieses Ergebnis addiere ich mit dem Zähler des Bruchteils. Das
ergibt den neuen Zähler, also in unserem Beispiel 10 plus 3 ergibt 13. 13 ist
der Zähler des unechten Bruches. Der Nenner des Bruchteils der gemischten
Zahl ist auch der neue Nenner, in unserem Fall 5.
Folie 5
Jetzt etwas zum Erweitern und Kürzen von Brüchen. Ich habe hier den Bruch 2
Drittel dargestellt. Ich will ihn mit 4 erweitern. Dazu teile ich jedes der
Teilrechtecke in vier gleich große neue Rechtecke beziehungsweise Quadrate.
Rechnerisch multipliziere ich den Zähler und den Nenner mit derselben Zahl.
© 2017 - matheguru.one
Textscript zum Aufgabenvideo „Addition und Subtraktion von Brüchen“ - Seite 2 von 4
Als nächstes möchte ich den Buch 3 Zwölftel durch 3 kürzen. Ich füge immer
nach drei kleinen Quadraten eine neue Teilung ein, sodass 4 gleich große
Rechtecke entstehen. Rechnerisch dividiere ich Zähler und Nenner durch
dieselbe Zahl.
Folie 6
Nun etwas zur Bildung des kleinsten gemeinsamen Vielfachen und des größten
gemeinsamen Teilers. Das kleinste gemeinsame Vielfache (kgV) ist hilfreich für
das Ordnen und Vergleichen von Brüchen und die Addition und Subtraktion von
Brüchen. In unserem Beispiel bilde ich das kgV von 15 und 18. Als erstes bilde
ich Vielfachenmengen. Dies erfolgt durch Multiplizieren der gewünschten Zahl
mit 1, 2, 3 und so weiter. Ich mache dies für 15 und erhalte als erste Vielfache
15, 30, 45, 60, 75, 90 und 105 und bei der 18 erhalte ich die Vielfachemenge,
deren erste Elemente die 18, 36, 54, 72, 90, 108 und 126 sind. Jetzt schaue
ich, welche kleinste Zahl in beiden Vielfachenmengen gleich sind. Dies ist die
90. Somit ist das kgV von 15 und 18 90.
Als nächstes ermittle ich das kgV durch eine kombinierte Multiplikation und
Division. Ich vervielfache die größere Zahl so lange, bis die kleinere Zahl ganz
hineinpasst. 18 mal 1 sind 18. Ich dividiere 18 durch 15, das Ergebnis ist 1
Rest 3. Dann multipliziere ich 18 mit 2, das Ergebnis ist 36. 36 geteilt durch 15
ist 2 Rest 6. Als nächstes nehme ich 18 mit 3 mal. Das Ergebnis ist 54. Bei der
Division durch 15 kommt 3 Rest 9 heraus. 18 mit 4 mal genommen ergibt 72,
die Division durch 15 ergibt 4 Rest 12 und 18 mal 5 sind 90. 90 geteilt durch
15 sind 6. Es bleibt kein Rest. Somit habe ich das kgV ermittelt, es ist 90.
Als dritte Möglichkeit zeige ich dir die Primfaktorenzerlegung. Eine Primzahl ist
eine natürliche Zahl, die nur 1 und sich selbst als Teiler hat. Die Primzahlen
unter 20 sind die 2, das ist die einzige gerade Primzahl, dann die 3, die 5, die
7, die 11, die 13, die 17 und die 19. Alle anderen Zahlen unter 20 haben mehr
als 2 Teiler. Ich zerlege die 15 in 3 mal 5 und habe bereits jetzt eine
vollständige Primfaktorenzerlegung durchgeführt. Die Lücken habe ich
gelassen, damit nachher gleiche Primzahlen untereinander stehen.
Aufgrund der Teilbarkeitsregeln dividiere ich die 18 erst einmal durch 2. 18
geteilt durch 2 ist 9. Ich zerlege die 9 noch einmal in 3 mal 3. Um das kgV zu
ermitteln, benötige ich alle Faktoren, die durch die Primfaktorenzerlegung
entstanden sind, das heißt, da die 3 zweimal auftritt, muss sie auch zweimal
im kgV enthalten sein, aber nicht mehr als das. Der Primfaktor 3, der in der 15
enthalten ist, wird nicht noch einmal aufgeschrieben. Somit sind die
notwendigen Primfaktoren für das kgV die 2, zweimal die 3 und die 5. Das
Ergebnis ist 90.
Jetzt zur Bildung des größten gemeinsamen Teilers. Das ist hilfreich für das
schnelle und vollständige Kürzen von Brüchen und die Ermittlung des
Basiswertes beim Dreisatz - das ist ein Thema, das meistens in der siebten
Klasse behandelt wird. Im Beispiel möchte ich den ggT von 36 und 48
bestimmen. Zunächst einmal bilde ich Teilermengen. Die Teiler von 36 sind 1,
2, 3, 4, 6, 9, 12, 18 und 36, die Teiler von 48 sind 1, 2, 3, 4, 6, 8, 12, 16, 24
und 48. Die größte Zahl, die in beidenTeilermengen vorhanden ist, ist die 12.
Somit ist der ggT von 36 und 48 die 12.
© 2017 - matheguru.one
Textscript zum Aufgabenvideo „Addition und Subtraktion von Brüchen“ - Seite 3 von 4
Als 2. Möglichkeit kann ich beide Zahlen jeweils durch die gleiche Zahl
dividieren und zwar solange, bis die Ergebnisse teilerfremd sind. Teilerfremd
bedeutet, dass die Ergebnisse nur noch den gemeinsamen Teiler 1 haben und
keinen weiteren gemeinsamen Teiler. Aufgrund der Teilbarkeitsregeln ermittle
ich, durch welche Zahlen ich beide Zahlen teilen kann. Ich teile 36 durch 2, das
ergibt 18. 48 durch 2 gleich 24.
Ich kann beide Zahlen auch durch 3 dividieren, die Ergebnisse sind 12 und 16,
ebenso durch 4. 36 durch 4 ist 9, 48 durch 4 ist 12 und auch durch 6, 36 durch
6 ist 6 und 48 durch 6 ist 8 sowie durch 12. 36 durch 12 ist 3 und 48 durch 12
ist 4. Die beiden Ergebnisse 3 und 4 sind teilerfremd. Der gemeinsame Teile
beider Zahlen ist nur noch die 1. Somit habe ich den ggT ermittelt. Der ggT
von 36 und 48 ist 12.
Zum Schluss auch hier die Primfaktorzerlegung. Ich zerlege 36 in 2 mal 18,
dann die 18 in 2 mal 9 und die 9 in 3 mal 3 Die 48 ist 2 mal 24, die 24 ist 2
mal 12, die 12 2 mal 6 und die 6 2 mal 3. Hier wähle ich nur die gemeinsamen
Faktoren aus. Ich habe die gleichen Faktoren untereinander geschrieben, so
dass ich es bei der Auswahl leichter habe. Die gleichen Primfaktoren, die bei
beiden Zahlen vorkommen, sind zweimal die 2 und einmal die 3. So ergibt sich
das Primfaktorenprodukt für den ggT von 36 und 48 von 2 mal 2 mal 3 und
das ist 12.
Folie 7
Jetzt etwas zur Addition und Subtraktion von ungleichnamigen Brüchen. Ich
habe hier zwei Brüche dargestellt, die ich addieren möchte. Die Brüche sind 2
Drittel und ein Viertel. Aus 3 und 4 ergibt sich der Hauptnenner 12. Damit ich
mich vollständig auf die Zähler konzentrieren kann, schreibe ich die Nenner
schon einmal hin und auch das Pluszeichen dazwischen.
Ich zeige dir hier in der Figur, wie es zeichnerisch gemacht wird und zwar
erweitere ich die beiden Figuren so, dass gleichgroße Bruchteile entstehen. Da
in den neuen Hauptnenner 12 der Nenner des ersten Bruches 3 viermal
hineinpasst, muss ich auch den Zähler mit 4 erweitern. 2 mal 4 ergibt 8. Der
Nenner des zweiten Bruches passt dreimal in den neuen Hauptnenner hinein,
also muss ich auch den Zähler mit 3 erweitern. Einmal 3 ergibt 3. In der Figur
sieht man, dass ich hinter die rötlichen Bruchteile die grauen Bruchteile
angefügt habe.
Rechnerisch addiere ich die Zähler, das heißt, 8 plus 3 ergibt 11. Der Nenner
des Ergebnisses ist auch der Hauptnenner, in diesem Fall 12. Das Ergebnis aus
der Addition von 2 Dritteln und ein Viertel ergibt also 11 Zwölftel.
Bei der Subtraktion gehe ich ähnlich vor. Ich ermittle den Hauptnenner, ich
erweitere die Brüche und in der Figur habe ich die grauen Bruchteile über die
rötlichen Bruchteili gelegt. An den Stellen, an denen beide zusammen
kommen, entferne ich die Bruchteile und es bleiben nur die Bruchteile übrig,
über die keine grauen Bruchteile gelegt wurden, in diesem Fall fünf von zwölf.
Das Ergebnis aus der Subtraktion von 2 Dritteln und ein Viertel ist also 5
Zwölftel.
© 2017 - matheguru.one
Textscript zum Aufgabenvideo „Addition und Subtraktion von Brüchen“ - Seite 4 von 4
Folie 8
Jetzt zur Lösung der Aufgabe. Die erste Aufgabe lautet 21 Zwanzigstel plus 15
Sechzehntel. Ich bilde den Hauptnenner, zuerst mit der Primfaktorenzerlegung.
20 ist 2 mal 10, 10 ist 2 mal 5 und 16 ist 2 mal 8, 8 ist 2 mal 4 und 4 ist 2 mal
2. Ich nehme wieder alle Faktoren, die ich ermittelt habe, unterstreiche sie und
füge sie zusammen. Das kgV von 20 und 16 ist also 2 mal 2 mal 2 mal 2 mal 2
mal 5, und ergibt 80.
Der Hauptnenner ist also 80. ich erweitere die Brüche, es ergibt sich für die
Aufgabe 84 Achtzigstel plus 75 Achtzigstel. Ich addiere die Zähler. Das
Ergebnis ist 159. Also lautet das Ergebnis 159 Achtzigstel. Da ich hier einen
unechten Bruch habe, muss ich diesen noch in eine gemischte Zahl
umwandeln. Das Ergebnis ist ein 79 Achtzigstel.
Zur zweiten Aufgabe. Hier habe ich zwei gemischte Zahlen, die ich addieren
soll. 2 2 Neuntel plus ein 11 Fünfzehntel. Ich bilde zuerst den Hauptnenner,
und zwar durch Bestimmung mit Hilfe von Vielfachenmengen. Die
Vielfachenmenge von 9 ist 9, 18, 27, 36, 45, 54, 63 und so weiter. Die
Vielfachenmenge von 15 beinhaltet 15, 30, 45, 60, 75, 90 und so weiter. Das
kleinste gemeinsame Vielfache von 9 und 15 ist 45. Der Hauptnenner ist also
45.
Um mir die Sache zu vereinfachen, addiere ich zunächst die ganzen Zahlen, 2
plus 1 sind 3, und erweitere die Brüche. Also ergibt sich 3 10
Fünfundvierzigstel plus 33 Fünfundvierzigstel, das heißt, ich habe die ganze
Zahl des zweiten Bruches zur ganzen Zahl des ersten Bruches addiert und
gleichzeitig die Brüche gleichnamig gemacht. Ich addiere die Zähler. 10 plus 33
sind 43 und erhalte als Endergebnis 3 43 Fünfundvierzigstel. Dadurch, dass ich
sofort die ganzen Zahlen addiert habe, muss ich jetzt nicht noch einmal einen
unechten Bruch in eine gemischte Zahl umwandeln, sondern erhalte diese
sofort.
In der letzten Aufgabe soll ich ein 24 Fünfundzwanzigstel minus 18 Zwanzigstel
rechnen. Ich wandle diesmal die gemischte Zahl in einen unechten Bruch um,
das ergibt 49 Fünfundzwanzigstel. Die Aufgabe heißt also jetzt 49
Fünfundzwanzigstel minus 18 Zwanzigstel, und ich bilde den Hauptnenner
durch die kombinierte Multiplikation und Division. 25 mal 1 sind 25. Ich teile
25 durch 20. Das ergibt 1 Rest 5. 25 mal 2 sind 50. 50 durch 20 sind 2 Rest
10. 25 mal 3 sind 75. Die Division durch 20 ergibt 3 Rest 15. 25 mal 4 sind
100. 100 durch 20 ergibt 5.
Es bleibt kein Rest. Somit habe ich das kgV bestimmt. Es ist 100. Das kgV von
25 und 20 ist 100. Ich erweitere die Brüche und erhalte in der Aufgabe 196
Einhundertstel minus 90 Einhundertstel. Ich subtrahiere die Zähler. 196 minus
90 und 106 und erhalte 106 Einhundertstel. Ich wandle in eine gemischte Zahl
um. Das erscheint mir im Moment leichter als sofort zu kürzen und erhalte ein
6 Einhundertstel und muss den Bruchteil der gemischten Zahl noch kürzen, da
6 und 100 als gemeinsam Teiler die 2 haben. Das Ergebnis ist ein 3 Fünfzigstel.
Damit habe ich die Aufgabe gelöst.
Folie 9
Weitere Tipps und Lösungen erhältst du auf matheguru.one.
© 2017 - matheguru.one