Addition und Subtraktion von Brüchen

mаtheguru.one
Tipps und Lösungen zu
Matheaufgaben aus Schulbüchern
Addition und Subtraktion
von Brüchen und gemischten Zahlen
●
●
●
●
Arten von Brüchen (echter Bruch, unechter Bruch, Scheinbruch)
Umwandeln: unechter Bruch ↔ gemischte Zahl
Erweitern und Kürzen von Brüchen
kleinstes gemeinsames Vielfaches (kgV)
und größter gemeinsamer Teiler (ggT), auch mit Primfaktorenzerlegung
© 2017 matheguru.one
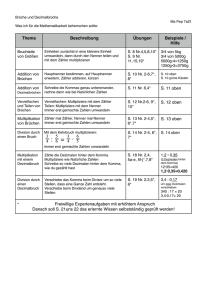
Schnittpunkt 6 (Allgemeine Ausgabe)
Seite 47, Nummer 5 f
Wandle das Ergebnis der Rechnungen wenn möglich in die gemischte Schreibweise um oder kürze.
© 2017 matheguru.one
Arten von Brüchen
Echter Bruch
Unechter Bruch
- Zähler ist kleiner als Nenner
- Bruchwert ist kleiner als 1
- Zähler ist größer als Nenner
- Bruchwert ist größer als 1
Scheinbruch
- Zähler ist Vielfaches des Nenners
- Bruchwert ist natürliche Zahl
Umwandeln: unechter Bruch ↔ gemischte Zahl
gemischte Zahl:
3
25
- Wie oft passt die 5 ganz in die 13?
2 mal → ganze (natürliche) Zahl
- Wie groß ist der Rest?
3 → neuer Zähler im Bruch
- Wie heißt der alte Nenner?
5 → auch der neue Nenner im Bruch
(13 : 5 = 2 Rest 3)
3
25
unechter Bruch:
13
5
neuer Zähler
Nenner bleibt gleich
Zahl mal Nenner
2 · 5 = 10
+
Ergebnis plus Zähler
10 + 3 = 13
© 2017 matheguru.one
Erweitern und Kürzen von Brüchen
Erweitern
Kürzen
- Multiplikation von Zähler und Nenner
mit derselben Zahl
Erweitern mit 4
- Division von Zähler und Nenner
durch dieselbe Zahl
Kürzen durch 3
© 2017 matheguru.one
kleinstes gemeinsames Vielfaches – größter gemeinsamer Teiler
Bildung des kgV
z. B. kgV(15, 18)
hilfreich für
- das Ordnen/ Vergleichen von Brüchen
- die Addition/ Subtraktion von Brüchen
1. Möglichkeit: Vielfachenmengen bilden
Bildung des ggT
z. B. ggT(36, 48)
hilfreich für
- das vollständige Kürzen von Brüchen
- die Ermittlung des Basiswertes beim Dreisatz
1. Möglichkeit: Teilermengen bilden
V15 = {15; 30; 45; 60; 75; 90; 105; ...}
T36 = {1; 2; 3; 4; 6; 9; 12; 18; 36}
V18 = {18; 36; 54; 72; 90; 108; 126; ...}
T48 = {1; 2; 3; 4; 6; 8; 12; 16; 24; 48}
ggT(36, 48) = 12
kgV(15, 18) = 90
2. Möglichkeit: Multiplikation/ Division
2. Möglichkeit: Division durch die gleiche Zahl
- größere Zahl solange vervielfachen,
bis kleinere Zahl ganz hineinpasst
18 · 1 = 18
18 : 15 = 1 Rest 3
18 · 2 = 36
36 : 15 = 2 Rest 6
18 · 3 = 54
54 : 15 = 3 Rest 9
18 · 4 = 72
72 : 15 = 4 Rest 12
18 · 5 = 90
90 : 15 = 6
kgV(15, 18) = 90
- beide Zahlen solange durch gemeinsame Teiler dividieren,
bis die Ergebnisse teilerfremd sind
36 : 2 = 18
48 : 2 = 24
36 : 3 = 12
48 : 3 = 16
36 : 4 = 9
48 : 4 = 12
36 : 6 = 6
48 : 6 = 8
36 : 12 = 3
48 : 12 = 4
3. Möglichkeit: Primfaktorenzerlegung
15 =
3
·5
18 = 2 · 9 = 2 · 3 · 3
3. Möglichkeit: Primfaktorenzerlegung
=2·2
·3·3
36 = 2 · 18 = 2 · 2 · 9
48 = 2 · 24 = 2 · 2 · 12 = 2 · 2 · 2 · 6 = 2 · 2 · 2 · 2 · 3
kgV(15, 18)
= 2 · 3 · 3 · 5 = 90
alle
Faktoren
Primzahl: hat als Teiler nur 1 und sich selbst
ggT(36, 48) = 12
ggT(36, 48)
gemeinsame
Faktoren
= 2 · 2 · 3 = 12
Primzahlen unter 20: 2; 3; 5; 7; 11; 13; 17 und 19
© 2017 matheguru.one
Addition und Subtraktion von ungleichnamigen Brüchen
Addition
·4
·4
·3
8
3
11
12
12
12
- Zähler addieren
- Nenner bleibt gleich
·3
Subtraktion
© 2017 matheguru.one
Aufgabe:
Wandle das Ergebnis der Rechnungen wenn möglich in die gemischte Schreibweise um oder kürze.
- Addition
der Zähler
kgV-Bestimmung durch Primfaktorenzerlegung
=2·2
·5
20 = 2 · 10
16 = 2 · 8 = 2 · 2 · 4 = 2 · 2 · 2 · 2
- Umwandlung in
gemischte Zahl
- Hauptnenner bilden
- Brüche erweitern
kgV(20, 16)= 2 · 2 · 2 · 2 · 5 = 80
- Addition
der Zähler
kgV-Bestimmung durch Vielfachenmengen
V9 = {9; 18; 27; 36; 45; 54; 63; ...}
V15 = {15; 30; 45; 60; 75; 90; ...}
- Hauptnenner bilden
- ganze Zahlen addieren
- Brüche erweitern
kgV(9, 15) = 45
- Hauptnenner bilden
- Brüche erweitern
- Umwandeln der
gemischten Zahl
in einen unechten
Bruch
- Umwandlung in
gemischte Zahl
- Subtraktion
der Zähler
- Kürzen
des Bruchs
kgV-Bestimmung durch Multiplikation/Division
25 · 1 = 25
25 : 20 = 1 Rest 5
25 · 2 = 50
50 : 20 = 2 Rest 10
25 · 3 = 75
75 : 20 = 3 Rest 15
25 · 4 = 100
100 : 20 = 5
kgV(25, 20) = 100
© 2017 matheguru.one
mаtheguru.one
Tipps und Lösungen zu
Matheaufgaben aus Schulbüchern
2
3