X - Hu-berlin.de

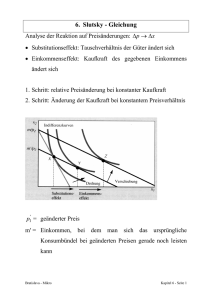
Die Slutsky-Gleichung
Was passiert, wenn der Preis eines Gutes steigt?
Normalerweise sollte bei einer Preissteigerung, p1, die
Nachfrage nach Gut 1 sinken...(Ausnahme: Giffen-Güter)
Ein Beispiel: Nach dem 2. WK ist der Fleischpreis extrem
angestiegen.
Die Wirkungen:
1.) Die Städter haben fast kein Fleisch mehr konsumiert.
2.) Die Bauern haben ihren Fleischkonsum erhöht.
Æ Warum? Æ Was passiert hier?
Æ Erklärung unterschiedlicher Verhaltensweisen mit dem
Instrumentarium der Haushaltstheorie...
1
Zerlegung einer Preisänderung von p1 in zwei Effekte:
1.) relative Preisveränderung
2.) Kaufkraftänderung
ODER:
1.) Substitutionseffekt
2.) Einkommenseffekt
2
1. Der Substitutionseffekt
Nachfrageänderung aufgrund der Veränderung der relativen Preise
p1 sinkt auf p1 '
„Drehung-Verschiebung“
x2
Kaufkraft wird konstant gehalten: D.h.,
das Einkommen wird so angepaßt, daß
bei den neuen relativen Preisen der alte
Konsumplan erreicht wird (i.e.: m‘).
m / p2
m' / p2
Z
Y
X
m / p1
m' / p '1
Drehung
X Æ Y: Substitutionseffekt
Y Æ Z: Einkommenseffekt
m / p '1
Verschiebung
x1
3
Genauer: Berechnung von m‘:
Der ursprüngliche Konsumpunkt ist ( x1 , x2 )
Dieser kann mit dem Einkommen m bei den Preisen (p1,p2) und beim
Einkommen m‘ bei den Preisen ( p1 ' , p2 ) realisiert werden.
p1 x1 + p2 x2 = m
(alte Budgetgerade)
p1 ' x1 + p2 x2 = m'
(neue Budgetgerade)
⇒ m − m' = x1 ( p1 '− p1 )
∆m = x1∆p1 mit
∆m := m'− m
∆p1 := p1 '− p1
⇒ sign(∆m) = sign(∆p )
4
Beispiel
Preis für Bier fällt von ¼DXI¼-
⇒ ∆p = −0,50
Bei ¼YHUEUDXFKW.DUO%LHUSUR:RFKH
Frage: Um wieviel Euro muß das Einkommen von Karl angepaßt
werden, so daß er gerade seinen alten Konsumplan realisieren
kann?
Antwort: Anwendung der Formel
∆m = x1∆p1 = 10 ∗ (−0,50) = −5¼
Beachte: Bei einer Preissenkung muß das Einkommen des
Verbrauchers gesenkt werden, um die Kaufkraft konstant zu halten.
Der Einkommenseffekt ist in diesem Fall positiv.
5
Optimierung bei neuer Budgetgeraden (X Æ Y)
Substitutionseffekt (SE): Der SE ∆x1s ist die Änderung der
Nachfrage nach Gut 1, wenn sich der Preis des Gutes 1 auf p1 ' ändert
und sich gleichzeitig das Geldeinkommen auf m‘ ändert.
∆x1s = x1 ( p1 ' , m' ) − x1 ( p1 , m)
Substitutionseffekt wird auch als Veränderung der kompensierten
Nachfrage bezeichnet.
6
Beispiel (Berechung des SE)
Die Nachfrage nach Gut 1 sei
x1 = 10 +
m
10 p1
Das Einkommen sei m=120 ¼XQGGHUXUVSUQJOLFKH
Preis sei p1=3,-- ¼
⇒ x1 (m, p1 ) = 14
Der Preis für das Gut 1 fällt nun auf p1‘=2,-- ¼ ! [⇒ x1 ( m, p1 ' ) = 16]
Berechung der neuen Budgetgeraden:
∆m = x1∆p1 = 14 ∗ (−1,00) = −14¼
⇒ m' = 120 − 14 = 106,00¼
⇒ x1 ( p1 ' , m' ) = x1 (2,106) = 15,30¼
∆x1s = x1 (2,106) − x1 (3,120) = 15,3 − 14 = 1,3
7
Das Vorzeichen des SE
Der SE bewegt sich immer entgegengesetzt zur Preisbewegung.
x2
Wir sagen. Der SE ist immer negativ!
Der SE führt hier zu einer Erhöhung der Nachfrage
X
Y
p1 sinkt!
Nicht möglich!
Also:
x1
sign(∆x1s ) = − sign(∆p)
8
Der Einkommenseffekt (EE)
(YÆZ)
Jetzt: Die Nachfrageänderung aufgrund der durch die Preisänderung
hervorgerufenen (realen) Einkommensveränderung.
Wir nehmen die neuen Preise und erhöhen das Einkommen von m‘
auf m.
x2
∆x1n = x1 ( p1 ' , m) − x1 ( p1 ' , m' )
m / p2
m' / p2
Z
Y
m' / p '1
m / p '1
x1
9
Das Vorzeichen des EE
(i) Bei normalen Gütern ist der EE negativ:
sign( ∆x1n ) = − sign(∆p1 )
Das heißt: Eine Preissenkung bewirkt eine Einkommenserhöhung
(m>m‘), so daß bei normalen Gütern die Nachfrage steigt.
(ii) Bei inferioren Gütern ist der EE positiv:
sign( ∆x1n ) = sign( ∆p1 )
Das heißt: Eine Preissenkung bewirkt eine Einkommenserhöhung
(m>m‘), so daß die Nachfrage nach dem inferioren Gut sinkt.
10
Beispiel (Forts.)
x1 = 10 +
m
10 p1
x1 (m, p1 ' ) = 16
x1 ( p1 ' , m' ) = 15,3
∆x1n = x1 ( p1 ' , m) − x1 ( p1 ' , m' )
∆x1n = 16 − 15,3 = 0,7
Gut 1 ist also ein normales Gut:
∆p1 = −1
∆x1n = +0,7
Die Nachfrage entwickelt sich entgegengesetzt zur Preisveränderung.
11
Die Slutsky-Gleichung (XÆ Z)
Die gesamte Veränderung der Nachfrage:
∆x1 = x1 ( p1 ' , m) − x1 ( p1 , m)
∆x1 = ∆x1s + ∆x1n
Slutsky-Identität
x1 ( p1 ' , m) − x1 ( p1 , m) = x1 ( p1 ' , m' ) − x1 ( p1 , m) + x1 ( p1 ' , m) − x1 ( p1 ' , m' )
Verwendung der Slutsky-Gl. zur Bestimmung der gesamten Nachfrageänderung
Normales Gut:
Inferiores Gut:
Wenn (+), dann
Giffen-Gut
∆x1 = ∆x1s + ∆x1n
(−) (−) (−)
∆x1 = ∆x1s + ∆x1n
(?) (−) (+)
Nachfrage
reagiert
entgegengesetzt
zur
Preisänderung
12
Anmerkungen
Ein Giffen-Gut muß also ein inferiores Gut sein.
Ein inferiores Gut ist nicht notwendig ein Giffen-Gut.
Gesetz der Nachfrage:
∆x1
<0
∆p1
Gilt immer für normale Güter.
13
Die Slutsky-Gleichung in Änderungsraten
Es sei
∆x1m := − ∆x1n
Dann ist die Slutsky-Gleichung
∆x1 = ∆x1s − ∆x1m
Dividieren durch ∆p auf beiden Seiten gibt
1
∆x1 ∆x1s ∆x1m
=
−
∆p1 ∆p1 ∆p1
Nutzen von ∆m = x1∆p1
oder
∆m
∆p1 =
x1
gibt
∆x1 ∆x1s ∆x1m
x1
=
−
∆p1 ∆p1 ∆m
Nachfrageänd. bei einer
Preisänderung und konst.
Kaufkraft
Einkommenseffekt
14
Beispiel: Rückvergütung einer Steuer
Um die Abhängigkeit von Ölimporten zu reduzieren, erwog der USKongreß die Einführung einer Benzinsteuer, die im Durchschnitt wieder
an die Verbraucher zurückgegeben werden sollte.
Frage: Wie stellen sich die Verbraucher bei einem solchen System?
Annahme: Die Steuer t wird 1:1 auf den Verbraucher überwälzt.
⇒ p' = p + t
Bei der neuen Steuer ist der Verbrauch des „durchschnittlichen“
Konsumenten x‘.
⇒ R = tx' = ( p '− p ) x'
15
Beispiel: Rückvergütung einer Steuer (Forts.)
Es sei y die Ausgabe für alle anderen Güter.
Alte Budgetgerade
px + y = m
Neue Budgetgerade
( p + t ) x'+ y ' = m + tx'
Rückvergütung
⇒ px'+ y ' = m
Das heißt, der neue Konsumplan liegt auf der alten Budgetgerade; war
daher vorher realisierbar.
Es wurde aber (x,y) gewählt und nicht (x‘,y‘), so daß gelten muß
( x, y ) ; ( x ' , y ' )
Also: Das Steuer-Rückvergütungssystem stellt den
„durchschnittlichen“ Verbraucher schlechter!
16
Hicks-Substitutionseffekt
Bestimmung des SE durch
„Rollen“ der Budgetgerade
entlang der ursprünglichen
Indifferenzkurve.
X
Z
Y
Die Hicks‘sche Nachfragekurve (bei konstantem Nutzen) wird auch als
kompensierte Nachfragekurve bezeichnet; hierbei ist das Nutzenniveau
auf allen Punkten der Nachfragekurve konstant.
17