Q - bei DuEPublico

2. Monopolistische Marktmacht
1
2 Monopolistische Marktmacht
2.
Überblick
„All competition is nothing, but striving for monopoly.“
Liefermann (1915)
„Like many businessmen of genius he learned that free competition was wasteful,
monopoly efficient.“
Mario Puzo (The Godfather, 1969)
• Es ist nützlich, sich zunächst die Extremform von Marktmacht
anzuschauen: das Monopol.
• Dieses Kapitel erklärt, warum ...
– Monopolmacht zu Ineffizienzen führt;
– Monopolmacht aber zugleich durch Marktkräfte beschränkt
werden kann.
2
Überblick
• Di
Die St
Standardanalyse
d d l
legt
l t nahe,
h dass
d Monopolmacht
M
l
ht einen
i
Wohlfahrtsverlust verursacht („statische Ineffizienz“).
• Zusätzlich kann ein Monopolist zu hohe Produktionskosten
aufweisen („produktive
( produktive Ineffizienz
Ineffizienz“)) und zu wenig in Forschung
und Entwicklung investieren („dynamische Ineffizienz“).
• Allerdings ist es nicht Aufgabe der Wettbewerbspolitik, die Zahl
der in einem Markt operierenden
p
Firmen unter allen Umständen
zu steigern.
• Dies kann zu ineffizienter Produktion führen und Fixkosten
replizieren, und damit wohlfahrtsschädigende Effekte haben.
3
Überblick
• Zudem stellt die Aussicht auf Gewinne für die Unternehmen
einen notwendigen Anreiz dar, in Forschung, Entwicklung und
Innovationen zu investieren.
• Schließlich, und das werden wir in Kapitel 2.2 sehen, können
Marktkräfte allein ausreichen, um den Monopolisten davon
abzuhalten seine Marktmacht auch auszunutzen
abzuhalten,
auszunutzen.
• Wettbewerbspolitik müsste dann trotz Monopolmacht nicht
aktiv werden.
4
2 1 Ineffizienz von Monopolen
2.1
2.1.1 Statische Ineffizienz
Was ist Marktmacht?
• Marktmacht beschreibt die profiterhöhende Fähigkeit eines
Unternehmens, die Preise vom Wettbewerbsniveau weg zu
bewegen.
• Typischerweise wird Marktmacht daher gemessen als Differenz
zwischen dem Preis und den Grenzkosten der Produktion.
• Die Ausnutzung von Marktmacht impliziert Ineffizienz.
5
2.1.1 Statische Ineffizienz
All k ti IIneffizienz
Allokative
ffi i
des
d M
Monopols
l
Die allokative Ineffizienz eines Monopols wird typischerweise
unter folgenden Annahmen demonstriert:
• Der Monopolist produziert bei konstanten Grenzkosten c. Die
Fixkosten seien der Einfachheit halber Null.
• Der Monopolist verwendet eine effiziente Technologie für die
P d kti
Produktion.
• Die Nachfragefunktion (OO
(OO´)) ist linear.
linear
6
p (q ) = a − bq
2.1.1 Statische Ineffizienz
π = p(q)q − cq
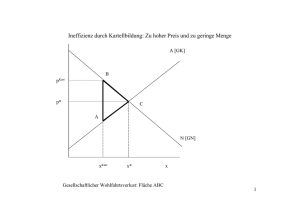
Abb 22.1
Abb.
1W
Wohlfahrtsverlust
hlf h t
l td
durch
hM
Monopoll
R = p (q )q = (a − bq)q
p
MR = a − 2bq
BEO : MR = c
a−c
M
q =
2b
O
MR
a+c
p = a − bq =
2
M
U
pm
πM
pc
S
T
M
1⎛a−c⎞
= ⎜
⎟
b⎝ 2 ⎠
2
c
O´
qm
qc
q
7
2.1.1 Statische Ineffizienz
• IIm Fall
F ll der
d vollständigen
ll tä di
Konkurrenz
K k
entspricht
t i ht der
d Preis
P i den
d
Grenzkosten (pc = c) . Zu diesem Preis wird die Menge qc
abgesetzt.
g
• Der Monopolist setzt den gewinnmaximalen Preis (bzw. die
gewinnmaximale Menge). Im Gewinnmaximum entsprechen
sich Grenzerlöse (MR) und Grenzkosten (c).
• Wenn der Preis über das Niveau der Grenzkosten gehoben wird,
entsteht ein gesamtwirtschaftlicher Wohlfahrtsverlust.
• Zwar steigt
g die Produzentenrente (PR);
( ) diese Erhöhung
g reicht
aber nicht aus, um den Verlust an Konsumentenrente (KR) zu
kompensieren.
8
2.1.1 Statische Ineffizienz
• IIm Monopolfall
M
lf ll steigt
t i t der
d Preis
P i auff pm. Die
Di abgesetzte
b
t t Menge
M
sinkt auf qm .
• Auswirkung auf die gesamtwirtschaftliche Wohlfahrt:
• Vollständige Konkurrenz: Gesamtwohlfahrt entspricht dem
Dreieck O pc S (entspricht der KR).
• Monopol: Gesamtwohlfahrt entspricht der Fläche O pc T U .
(Di PR steigt
(Die
t i t um die
di Fläche
Flä h pm pc T U
U, die
di KR ist
i t auff die
di
Fläche O pm U gesunken).
• Es entsteht ein Netto-Wohlfahrtsverlust in Höhe von U T S.
9
2.1.1 Statische Ineffizienz
• Di
Dieses St
Standardmodell
d d d ll vernachlässigt
hlä i t eine
i ganze Reihe
R ih von
wichtigen Aspekten:
• Welche weiteren Quellen der Ineffizienz gibt es bei
Monopolmacht?
• Gibt es auch Quellen der Effizienz?
• Was ppassiert bei Markteintritt?
• Was passiert, wenn sich der Monopolist nicht glaubwürdig
darauf verpflichten
p
kann, den Preis konstant zu halten?
• Was passiert, wenn der Monopolist Preise diskriminieren
kann?
• Wo ist überhaupt das Problem, wenn die regulierende
Behörde all diese Informationen hat?
10
2.1.1 Statische Ineffizienz
R t S ki
Rent-Seeking
• Zusätzlich kann auch die Monopolrente zum Wohlfahrtsverlust
werden.
d
• Dies kann passieren, wenn Unternehmen Mittel aufwenden, um
ihre Monopolmacht zu erhalten oder zu vergrößern.
• Posner (1975) schreibt:
„The existence of an opportunity to obtain monopoly profits will
attract ressources into efforts to obtain monopolies, and the
opportunity costs off these
h
resources are sociall costs off
monopoly too.“
• Diese Mittel können also unproduktiv sein, etwa die
Beschäftigung von Anwälten, politische Einflussnahme, etc.
11
2.1.1 Statische Ineffizienz
Abb 22.2
Abb.
2 Mö
Möglicher
li h Z
Zusatzverlust
t
l td
durch
hR
Rent-Seeking
t S ki
p
O
MR
U
pm
pc
Argument von Posner (1975):
Der mögliche Zusatzverlust
kann der Höhe des gesamten
Monopolgewinns
entsprechen.
S
T
c
O´
qm
qc
q
12
2.1.1 Statische Ineffizienz
• Idee: Die Firmen konkurrieren um die Monopolstellung, die
einen (erwarteten) Monopolgewinn verspricht.
• Ist der Konkurrenzkampf
p stark,, werden alle ((erwarteten))
Gewinne durch den Einsatz von Ressourcen wegkonkurriert.
• Folglich werden die (erwarteten) Gewinne im Wettbewerb um
das Monopol aufgefressen.
13
2.1.1 Statische Ineffizienz
P
Posner
(1975)
(1975), T
Tullock
ll k (1967,
(1967 1980):
1980)
Beachte:
B
ht Der
D V
Verlust
l t ddurchh R
Rent-Seeking
t S ki Akti
Aktivitäten
ität entsteht
t t ht zusätzlich
ät li h zum
Wohlfahrtsverlust durch das Monopol.
Beispiel: 5 Firmen stehen im Wettbewerb um eine Monopolstellung.
Der erwartete Gewinn aus der Monopolstellung beträgt 100.000 €.
Für alle Firmen ist ein gleichermaßen wahrscheinlich, die
Monopolstellung zu erhalten, d.h. jede Firma erwartet einen Gewinn
von 20
20.000
000 €.
€
)
Für jjede Firma ist es rational,, bis zu 20.000 € in Rent-Seeking
g
Aktivitäten zu investieren.
→ “full
full rent dissipation”
dissipation
14
2.1.1 Statische Ineffizienz
Tullocks Rent
Rent-Seeking
Seeking Modell
• Es gibt zwei identische Interessengruppen (i = 1, 2), die sich beide
risikoneutral
i ik
t l verhalten.
h lt
• Beide Interessengruppen wählen simultan ihre Ausgaben für RentSeeking Aktivitäten xi
.
•
pi ist die Erfolgswahrscheinlichkeit und ist bestimmt durch
•
der erwartete Profit durch die Monopolstellung ist π
pi =
xi
xi + x j
•
Wir nehmen an, dass beide Interessengruppen Rent-Seeking
Akti ität durchführen
Aktivitäten
d hfüh
undd dass
d die
di Gruppe
G
mit
it den
d höchsten
hö h t
Ausgaben auch die höchste Erfolgswahrscheinlichkeit hat.
•
der erwartete Gewinn der Interessengruppe i ist:
Fi (xi , x j ) = pi ⋅ π − xi =
xi
⋅ π − xi
xi + x j
15
2.1.1 Statische Ineffizienz
→ Das Maximierungskalkül der Interessengruppe i (gegeben die RentSeeking Ausgaben xj der Gruppe j) lautet:
max Fi (xi , x j ) = pi ⋅ π − xi
xi
B.1.O.:
!
∂pi
⋅ π − 1= 0
∂xi
weil:
x j > 0,
∂pi
1
1
=
− xi
=
2
∂xi xi + x j
( xi + x j )
( xi + x j ) 2
erhalten wir:
xj
⋅π =
1
{
(x + x j )
1i42
4 43
4 marginal costs
2
marginal revenue
16
2.1.1 Statische Ineffizienz
Führen höhere Ausgaben der anderen Gruppe zu höheren Ausgaben der
eigenen Gruppe?
→ Beste-Antwort-Funktion
A
k i der
d Gruppe
G
i: xi ( x j ) =
xj ⋅ π − xj
xi
π
xj(xi)
π
*
(xi*=x0.25
i = )
xi(xj)
4
π
(xxj**=
j =0.25)
4
π
xj
17
2.1.1 Statische Ineffizienz
N h Gl i h
Nash-Gleichgewicht:
i ht
Die Symmetrieannahme
y
impliziert,
p
, dass im Gleichgewicht
g
xi = xj .
Einsetzen dieser Gleichgewichtsbedingung in die B.E.O. und Umstellen
ergibt:
g
1
xi
1
*
⇔
⋅
π
=
1
⇒
⋅
π
=
1
x
=
⋅ π = x*j
2
i
( xi + xi )
4 xi
4
Konsequenz für die Wohlfahrt
A
Aggregation
ti der
d Ausgaben
A
b der
d beiden
b id Interessengruppen
I t
ergibt:
ibt
1
π
*
x
n
=
⋅
⋅
π
=
∑
s
4
2
s =1
n
Was passiert, wenn mehr als zwei Interessengruppen miteinander
konkurrieren? Wird der Wohlfahrtsverlust steigen oder sinken?
18
2.1.1 Statische Ineffizienz
→ Wenn
W
wir
i weiterhin
it hi identische
id ti h Interessengruppen
I t
unterstellen,
t t ll können
kö
wir
i
das Gleichgewicht für den n-Personen Fall unter Ausnutzung der
Symmetriebedingung bestimmen (xi = xj).
Aus der Perspektive der Gruppe i gibt es nun n – 1 andere Gruppen j. Das
heißt, die individuelle B.E.O. ist
(n − 1) ⋅ x j
( xi + (n − 1) ⋅ x j ) 2
Umstellen ergibt:
⋅π =1⇒
( n − 1) ⋅ xi
⋅π =1
2
2
n ⋅ xi
(n − 1) ⋅ xi
⋅π =1
2
( xi + (n − 1) ⋅ xi )
⇔
xi* =
n −1 π
⋅
n n
Konsequenz für die Wohlfahrt:
n
*
x
∑ s = n⋅
s =1
n −1 π n −1
⋅ =
⋅π
n n
n
Gesamtausgaben
19
2.1.1 Statische Ineffizienz
Rent-seeking in Abhängigkeit von der Anzahl der Gruppen:
1
0,9
0,8
0,7
06
0,6
0,5
0,4
0,3
02
0,2
0,1
0
0
1
2
3
4
5
6
7
8
9
10
→ Die Gesamtausgaben steigen in der Anzahl der Gruppen. In unserem
p betragen
g die Gesamtausgaben
g
bei n = 10 bereits 90% des
Beispiel
erwarteten Monopolgewinns.
→ 50% im Fall n = 2 ist also der geringste Wohlfahrtsverlust, der durch
Rent-Seeking ausgelöst wird!
20
2.1.1 Statische Ineffizienz
Allgemeineres Modell:
•
pi ist die Erfolgswahrscheinlichkeit
g
und ist bestimmt durch
r
xi
pi = r
r
xi + x j
•
r ist ein Parameter, der die Wettbewerbsintensität misst
→ Nash-Gleichgewicht (2 Interessengruppen):
r ⋅π
x =
4
*
i
→ Bereits “full rent dissipation“ für r = 2!
Was passiert, wenn r > 2?
→ Es gibt kein Nash-Gleichgewicht in reinen Strategien!
→ “Tullock swamp”
21
2.1.1 Statische Ineffizienz
• Aber: Die eingesetzten Mittel müssen nicht notwendigerweise
unproduktiv sein.
• Manchmal werden Entdeckungen, die zu Monopolen führen,
‚zufällig‘
zufällig‘ gemacht.
gemacht
• Patentrennen duplizieren zwar Fixkosten, können aber auch
wohlfahrtssteigernd
hlf h t t i
d wirken.
ik
• Werbung und Lobbyarbeit kann wertvolle Informationen
erzeugen.
• Wie sieht es mit Bestechung aus?
• Eine wettbewerbspolitische Implikation: Auktionen erzeugen
keine Ineffizienzen (siehe Kapitel 3.2.5).
22
212P
2.1.2
Produktive
d kti IIneffizienz
ffi i
Idee:
Ein Monopolist produziert mit höheren Kosten als Firmen
Firmen,
die Wettbewerb ausgesetzt sind.
Dadurch entstehen über die statischen Ineffizienzen hinaus
zusätzliche Wohlfahrtsverluste.
23
2.1.2 Produktive Ineffizienz
Abb 22.3
Abb.
3Z
Zusatzverlust
t
l td
durch
hP
Produktive
d kti IIneffizienz
ffi i
p
p´m
O
U´
MR
U
pm
p´c
pc
W
V
Z
T´
T
c´
S
T
c
O´
qq´m qm
qc
q
24
2.1.2 Produktive Ineffizienz
• A
Annahme:
h
D
Der M
Monopolist
li t hat
h t höhere
höh P
Produktionskosten
d kti k t (c
( `))
als die Firmen in vollständiger Konkurrenz (c).
• Würde der Monopolist mit der effizienten Technologie c
produzieren, ergäbe sich wie in 2.1.1 der Monopolpreis pm und
eine Wohlfahrtsverlust in Höhe von U T S.
• Mit
i c‘‘ wählt
hl der
d Monopolist
li einen
i
höheren
h h
Preis
i p´´m. Der
gesamte Wohlfahrtsverlust ergibt sich dann aus der Summe der
Flächen U
U´ T
T´ S und pp´c pc.c T
T´ V.
• Der zusätzliche Verlust, der sich aufgrund
g
der ineffizienten
Produktionsweise des Monopolisten ergibt, ist in Abb. 2.3 als
blau schraffierte Fläche dargestellt.
25
2.1.2 Produktive Ineffizienz
Wieso kann es zu produktiver Ineffizienz kommen?
Nachlässigkeit des Managements – „Managerial Slack“:
•
Idee: Entscheidungen werden nicht von den Kapitaleignern
selbst, sondern von den Managern des Unternehmens als deren
Beauftragte
f
getroffen.
ff
•
Principal-Agent-Problem:
P
i i l A t P bl
Der
D M
Manager als
l A
Agentt hhatt evtl.
tl
andere Zielsetzungen als der Kapitaleigner, der an der
Maximierungg der erzielten Gewinne interessiert ist.
26
2.1.2 Produktive Ineffizienz
• Ei
Ein großer
ß Teil
T il der
d Management-Literatur
M
t Lit t beschäftigt
b häfti t sich
i h mit
it
der Frage, wie Manageranreize richtig gesetzt werden müssen.
• Wettbewerb zwingt Manager automatisch, effizient zu
produzieren, da sonst das Unternehmen aus dem Markt gedrängt
wird.
• Die
i Empirie
i i scheint
h i dieser
di
These
h
recht
h zu geben:
b
• die Effizienz eines Unternehmens hängt positiv von der
Konkurrenzsituation ab (z.B.
(z B Nickell,
Nickell Nicolitsas und Dryden
1997),
• die Produktivität einer Branche hängt
g negativ
g
von dem
Konzentrationsgrad (z.B. Disney et al. 2000)
• und positiv von den Ein- bzw. Austrittsaktivitäten ab (Olley
undd Pakes
P k 1996)
1996).
27
2.1.2 Produktive Ineffizienz
• Selektionsdruck kann aber auch dazu führen, dass Unternehmen
vom Markt verschwinden und dadurch der Wettbewerb ceteris
paribus wieder schwächer wird.
• Wi
Wir werden
d gleich
l i h in
i einem
i
Cournot-Modell
C
M d ll zeigen,
i
dass
d
Wettbewerb auf Kosten von ineffizienter Produktion (hohen
Grenzkosten)) letztlich nicht wohlfahrtssteigernd
g
ist.
• Danach werden wir in unser Cournot-Modell Fixkosten
einführen und sehen, dass die gesamtwirtschaftlich produktive
Effizienz zuweilen eine Monopolstellung bedingt!
• Beide Modelle zeigen, dass nicht nur zuwenig, sondern auch
‚zuviel
zuviel‘ Konkurrenz der produktiven Effizienz schaden kann.
kann
28
2.1.2 Produktive Ineffizienz
M d ll P
Modell:
Produktive
d kti IIneffizienz
ffi i
und
d Selektionsdruck
S l kti d k
Annahmen
• Auf einem Markt werden homogene Güter gehandelt.
gehandelt
g
• Cournot-Mengenwettbewerb.
• Die Unternehmen sind unterschiedlich produktiv.
nk
Firmen produzieren zu hohen Grenzkosten ch < 1.
n(1 – k) Firmen produzieren zu niedrigen Grenzkosten cl < ch.
• Lineare Marktnachfrage
p = 1− Q
mit Q = aggregiertes
Angebot
29
2.1.2 Produktive Ineffizienz – Modell: Produktive Ineffizienz und Selektionsdruck
• Für
Fü die
di Angebotsmenge
A b t
Q gilt:
ilt
Q = ∑ qi + ∑ q j
i∈L
, wobei
b i
j∈H
L und H für die Menge der Firmen mit niedrigen bzw.
bzw hohen
Kosten stehen.
• Gewinnfunktionen der Firmen:
π i = ( p(Q ) − cl ) qi
π j = ( p(Q ) − ch ) q j
∀i ∈ L
∀j ∈ H
oder:
d
⎛
⎞
π i = ⎜⎜1 − ∑ qi − ∑ q j ⎟⎟ qi − cl qi
j∈H
⎝ i∈L
⎠
⎛
⎞
π j = ⎜⎜1 − ∑ qi − ∑ q j ⎟⎟ q j − ch q j
⎝
i∈L
j∈H
⎠
30
2.1.2 Produktive Ineffizienz – Modell: Produktive Ineffizienz und Selektionsdruck
• B
Bedingungen
di
erster
t Ordnung
Od
(unter Anwendung der Produktregel):
∂π i !
= 0 ⇔ − qi + 1 − ∑ qi − ∑ q j − cl = 0,
∂qi
i∈L
j∈H
(2.1)
∂π j !
= 0 ⇔ − q j + 1 − ∑ qi − ∑ q j − ch = 0,
∂q j
i∈L
j∈H
(2.2)
• Da die Firmen mit hohen und niedrigen Kosten jeweils
symmetrisch sind, gilt:
∑ qi = n(1 − k )ql
i∈L
∑ q j = nkqh
j∈H
31
2.1.2 Produktive Ineffizienz – Modell: Produktive Ineffizienz und Selektionsdruck
• Wi
Wirdd dies
di in
i (2.1)
(2 1) undd (2.2)
(2 2) eingesetzt,
i
t t so kann
k
man vereini
fachend schreiben:
1 − cl − nkqh und q = 1 − ch − n(1 − k )ql
h
ql =
1 + nk
1 + n(1 − k )
(2.3)
mit ql : Output der Firma mit geringen Kosten
qh : Output der Firma mit hohen Kosten
32
2.1.2 Produktive Ineffizienz – Modell: Produktive Ineffizienz und Selektionsdruck
• Für die Outputwerte ergibt sich durch gegenseitiges Einsetzen:
ql =
*
1 − cl + nk (ch − cl )
1+ n
qh* =
bzw.
1 − ch − n (1 − k )(ch − cl )
1+ n
• Der zugehörige Preis lautet:
1 + nkch + n(1 − k )cl
*
p =
1+ n
(2 4)
(2.4)
33
2.1.2 Produktive Ineffizienz – Modell: Produktive Ineffizienz und Selektionsdruck
• Zum Beispiel gilt für n = 2 und k = 1/2:
ql =
*
1 − 2cl + ch
3
bzw.
1 − 2ch + cl
qh =
3
*
• Der zugehörige Preis und Gewinn lautet:
(1 − 2ci + c j )
1 + cl + ch
*
p =
und
d πi =
9
3
2
• Aber
b Achtung:
h
eine
i Firma
i
produziert
d i nur, wenn sie
i positive
ii
Gewinne macht. Die BEO ist in diesem Fall nicht hinreichend.
Falls p* ≤ ch treten die Firmen mit den hohen Kosten aus dem
Markt aus!
34
2.1.2 Produktive Ineffizienz – Modell: Produktive Ineffizienz und Selektionsdruck
• Für
Fü die
di Fi
Firmen mit
it hohen
h h Kosten
K t muss also
l gelten:
lt p* ≥ ch .
Dies gilt nur dann,
dann wenn
1 + n(1 − k )cl
ch ≤
1 + n(1 − k )
(2.5)
• Diese Bedingung
g g wird umso restriktiver,, jje mehr Firmen im
Markt agieren, also je größer der Wert für n ist.
• Der Selektionsdruck ist umso größer, je größer die
Konkurrenzsituation ist.
• Produktive Ineffizienz verschwindet bei starker Konkurrenz.
35
2.1.2 Produktive Ineffizienz – Modell: Produktive Ineffizienz und Selektionsdruck
• L
Langfristig,
f i ti bei
b i endogenem
d
Markteintritt,
M kt i t itt gibt
ibt es somit
it kein
k i
Problem. Positive Gewinne sorgen zunächst dafür, dass n steigt
bis schließlich die ineffizienten Firmen heraus ggedrängt
g werden.
• Der Konkurrenzdruck unter den effizienten Firmen wird dann
schließlich
hli ßli h dazu
d
führen,
füh
dass
d sich
i h Preise
P i langfristig
l f i ti den
d
Grenzkosten cl annähern.
• Langfristig gibt es also kein Problem. Aber kurzfristig, wenn die
ineffizienten Firmen verdrängt werden, scheint es aus Sicht der
Wettbewerbsbehörde einen Zielkonflikt zu geben:
• Auf der einen Seite führen Marktaustritte kurzfristigg zu weniger
g
Anbietern und damit geringerem Preisdruck.
• A
Auff der anderen Seite ist die Produktion
Prod ktion durchschnittlich
d rchschnittlich
effizienter.
36
2.1.2 Produktive Ineffizienz – Modell: Produktive Ineffizienz und Selektionsdruck
• E
Es gilt
ilt aber,
b dass
d die
di V
Verdrängung
dä
auchh kurzfristig
k f i ti vorteilhaft
t ilh ft ist
it
– der Marktpreis nach den Marktaustritten muss fallen!
• Beweis: Angenommen, der Markt besteht nur aus den n(1 – k)
Firmen, die zu niedrigen Kosten produzieren können. Diese
wählen ihren Output gemäß (2.3), wobei nun gilt: qh = 0.
• Also
Al beträgt
b
der
d Output
O
jjeweils:
il
1 − cl
**
ql =
1 + n(1 − k )
• Für den Preis folgt:
1 + n(1 − k )cl
p =
1 + n(1 − k )
**
(2.6)
37
2.1.2 Produktive Ineffizienz – Modell: Produktive Ineffizienz und Selektionsdruck
• U
Unter
t welcher
l h Bedingung
B di
gilt
ilt nun, dass
d bei
b i Marktaustritt
M kt t itt der
d
Preis fällt, d.h. p* > p**? Aus (2.4) und (2.6) folgt:
1 + nkc
k h + n(1 − k )cl 1 + n(1 − k )cl
>
1+ n
1 + n(1 − k )
[
1 + n(1 − k )cl ](1 + n ) [n(1 − k )cl ](1 + n(1 − k ))
1 + nkch >
−
1 + n(1 − k )
1 + n(1 − k )
(1 + n ) nk [n(1 − k )cl ]
− [1 + n(1 − k )]
nkch >
+
+
1 + n(1 − k ) 1 + n(1 − k ) 1 + n(1 − k )
1 + n(1 − k )cl
ch >
1 + n(1 − k )
• Dies ist die gleiche Bedingung, unter der Firmen mit hohen
Kosten aus dem Markt ausscheiden müssen (vgl. (2.5)).
38
2.1.2 Produktive Ineffizienz – Modell: Produktive Ineffizienz und Selektionsdruck
• D.h. die gewinnmaximale Markteintritts- und
austrittsentscheidung ‘maximiert’ den Preisdruck und trägt
d d h zur W
dadurch
Wohlfahrt
hlf h bei.
b i
• Weder sollte man ineffiziente Firmen künstlich aus einem Markt
zu drängen versuchen, …
• … noch macht es Sinn, ineffiziente Firmen der Konkurrenz
willen zu subventionieren.
• Auch kurzfristig ist Marktaustritt positiv zu bewerten, denn er
erlaubt
l b die
di Reallokation
R ll k i der
d Produktion
P d k i auff effizientere
ffi i
Firmen.
Fi
39
2.1.2 Produktive Ineffizienz
Eine andere
Ei
d
Si
Sicht:
ht M
Monopole
l als
l G
Garantt fü
für
gesamtwirtschaftlich produktive Effizienz!?
• Bisher haben wir argumentiert, dass Monopole auf dem
Unternehmenslevel zu produktiver Ineffizienz führen können.
• Zuweilen ist es jedoch für die gesamtwirtschaftliche produktive
Effizienz
ff
gerade
d notwendig,
di Monopole
l zu dulden.
d ld
• B
Beii langfristiger
l f i ti
Betrachtung
B t ht
undd hohen
h h Fixkosten
Fi k t existiert
i ti t
nämlich ein Zielkonflikt:
• JJe größer
öß di
die Zahl
Z hl der
d Firmen,
Fi
desto
d t größer
öß der
d
Konkurrenzdruck; aber auch:
• desto größer die Summe der Fixkosten,
Fixkosten die von den
Unternehmen im Markt getragen werden muss.
40
2.1.2 Produktive Ineffizienz
M d ll Konkurrenz
Modell:
K k
und
d Fixkosten
Fi k t
Annahmen
• Markt mit homogenem Gut und n symmetrischen Firmen
Firmen.
g
• Cournot-Mengenwettbewerb.
• (Identische) Kostenfunktion der Firmen:
mit c = konstante Grenzkosten
F > 0 Fixkosten (unabhängig von Ausbringungsmenge)
• Inverse Marktnachfrage p(Q) = a – bQ
41
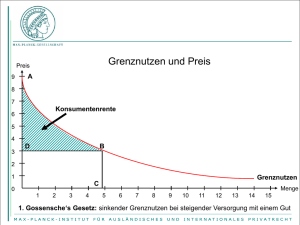
2.1.2 Produktive Ineffizienz
Ill t ti
Illustration
p
p(Q) = a – bQ
AC(q) = c + F/q > c
MC(q) = c
Q
42
2.1.2 Produktive Ineffizienz – Modell: Konkurrenz und Fixkosten
• Wir haben es hier mit einem sogenannten ‚natürlichen
Monopol‘ zu tun.
Monopol
• Die Durchschnittskosten ((cqq + F)/q
) q fallen für alle q, so dass
jede positive Ausbringungsmenge effizient nur durch eine Firma
erbracht werden kann.
• Dies gilt z.B. typischerweise in leitungsgebundenen Industrien.
• Aus wohlfahrtstheoretischer Sicht führt jede Konkurrenz zu
gesamtwirtschaftlich produktiver Ineffizienz!
• Ein Regulierer
g
würde also,, wenn er kann,, ein Monopol
p
installieren und Grenzkosten vorschreiben.
43
2.1.2 Produktive Ineffizienz
Ill t ti
Illustration
p
p(Q) = a – bQ
First-best (Regulierung)
AC(q) = c + F/q > c
MC(q) = c
pc
Q*
Q
44
2.1.2 Produktive Ineffizienz – Modell: Konkurrenz und Fixkosten
• Di
Die Regulierung
R li
natürlicher
tü li h Monopole
M
l ist
i t nicht
i ht Gegenstand
G
t d der
d
Wettbewerbspolitik im engeren Sinne.
• Einige typische Unterschiede zwischen Wettbewerbspolitik und
Regulierung:
• Wettbewerbspolitik beschäftigt sich mit Strukturen, die prinzipiell mit
Wettbewerb kompatibel
p
sind,, und überprüft
p
typischerweise
yp
ex p
post die
Gesetzmäßigkeit von Marktaktivitäten.
• Regulierer beschäftigen sich mit nicht-wettbewerblich
nicht wettbewerblich organisierbaren
Branchen, haben mehr Macht (Preiskontrolle etc.) und werden
typischerweise eher ex ante aktiv.
• Methodisch: Wettbewerbspolitik bedient sich i.d.R. der Oligopoltheorie,
während Regulierungstheorie vornehmlich Prinzipal-Agenten Modelle
nutzt.
t t
45
2.1.2 Produktive Ineffizienz – Modell: Konkurrenz und Fixkosten
• All
Allerdings
di
ist
i t es aufgrund
f
d von Informationsproblemen
I f
ti
bl
unwahrscheinlich, dass ein Regulierer das first-best Optimum
identifizieren und implementieren
p
kann.
• (Könnte er dies, wäre auch die Wettbewerbspolitik überflüssig.)
• Im Folgenden nehmen wir also an, Regulierung ist nicht
möglich.
li h Wie
i weit
i kann
k
man mit
i Wettbewerb
b
b kommen?
k
?
• A
Auch
hW
Wettbewerb
ttb
b kkann niemals
i
l zu first-best
fi t b t Allokationen
All k ti
führen, denn bei Grenzkostenpreisen werden Verluste gemacht.
• Aber ist Wettbewerb einer Monopolstellung vorzuziehen?
Kommen wir zurück zu unserem Cournot-Modell mit Fixkosten:
46
2.1.2 Produktive Ineffizienz – Modell: Konkurrenz und Fixkosten
• Da die Fixkosten kurzfristig keine Rolle spielen (wohl aber
langfristig bei Markteintrittsentscheidungen), impliziert die
BEO für eine gegebene Anzahl von Anbietern zunächst das
Standard Cournot-Resultat für die Mengenentscheidung:
a−c
b(n + 1)
n a−c
C
Q =
n +1 b
a−c
pC =
+c
n +1
qC =
1⎛a−c⎞
πC = ⎜
⎟ −F
b ⎝ n +1 ⎠
2
47
2.1.2 Produktive Ineffizienz – Modell: Konkurrenz und Fixkosten
• In der langen Frist, bei freiem Markteintritt, werden jedoch
solange Firmen ein
ein- oder austreten, bis der Gewinn Null ist.
• Dies ggibt uns eine Optimalbedingung
p
g g für die Anbieterzahl im
langfristigen Gleichgewicht:
1⎛a−c⎞
πC = ⎜
⎟ −F =0
b ⎝ n +1 ⎠
a−c
⇒ n +1 =
bF
2
• Die Zahl der Anbieter n im langfristigen Gleichgewicht hängt
also positiv von a und negativ von den Grenz
Grenz- und Fixkosten c
und F sowie von b ab.
48
2.1.2 Produktive Ineffizienz – Modell: Konkurrenz und Fixkosten
• W
Wenn also
l die
di Fi
Fixkosten
k t nicht
i ht zu hoch
h h sind,
i d führt
füh t freier
f i
Marktein- und austritt zu Wettbewerb zwischen mehreren
Firmen ((insbesondere ggilt für F → 0,, dass n → ∞).
)
• Je größer die Anzahl der Firmen, desto geringer ist der Preis,
desto höher der Output und desto größer die KR.
• Da jede
j d Firma
i
Fixkosten
i k
verursacht
h führt
f h Markteintritt
k i i jedoch
j d h
zu Überkapazitäten; nur ein Monopol kann für
gesamtwirtschaftlich produktive Effizienz sorgen.
• Wettbewerbspolitik
p
muss diese beiden gegenläufigen
g g
g Effekte
auf KR und PR abwägen. Insbesondere ist es (in Abwesenheit
von Regulierung) wichtig zu wissen, ob freier Marktzutritt
besser ist als ein geschütztes Monopol:
49
2.1.2 Produktive Ineffizienz – Modell: Konkurrenz und Fixkosten
• Angenommen,
A
a = b = 1 und
d c = 0.
0
• Dann gilt bei freiem Marktzutritt (siehe oben):
QC = n/(n + 1)
1
• Die Gleichgewichtsbedingung für n ist dann:
n + 1 = 1/ F
KR = (1 – p)2 /2
p
p(Q) = 1 – Q
• Also folgt für QC im langfristigen Gleichgewicht:
QC = 1 − F
• Die PR ist Null (freier Marktein- und austritt), und die KR ist
identisch mit der Wohlfahrt WC gleich:
(1 − p ) 2 (1 − (1 − (1 − F )))2 (1 − F ) 2
KR = W =
=
=
2
2
2
C
50
2.1.2 Produktive Ineffizienz – Modell: Konkurrenz und Fixkosten
• Fü
Für ddas Monopol
M
l gilt:
ilt
QM = 1/2
• Das Monopol produziert nur dann, wenn der Gewinn positiv ist:
1
1
M
π = −F >0⇔ F <
4
4
• Die KR im Monopolfall ist:
(1 − (1 − 1 / 2)) 2 1
KR =
=
2
8
• Also folgt für die Wohlfahrt:
1
1 3
WM = −F + = −F
4
8 8
51
2.1.2 Produktive Ineffizienz – Modell: Konkurrenz und Fixkosten
• Ei
Ein Vergleich
V l i h der
d W
Wohlfahrt
hlf h t im
i Cournot-Wettbewerb
C
t W ttb
b undd im
i
Monopolfall zeigt, dass Wettbewerb dann besser ist, wenn die
Fixkosten F hinreichend niedrigg sind:
WC >W M ⇔
1
> F (2 − 3 F )
4
• Dies gilt für F < 0,028
(bei F > 0,25 tritt keine Firma in den Markt ein; s.o.)
• Bei hinreichend geringen Fixkosten ist in unserem Modell
‚natürlicher Monopole
Monopole‘ Wettbewerb einer Monopolstellung
vorzuziehen.
• Bei hinreichend hohen Fixkosten ist Wettbewerb
wohlfahrtsschädlich.
52
2.1.2 Produktive Ineffizienz
F it
Fazit
• Fehlender Wettbewerb führt zu statischer und produktiver
Ineffizienz.
• Gleichwohl ist mehr Konkurrenz per se weder eine gute noch
eine schlechte Sache.
• Wettbewerb um Monopolrenten kann zu weiteren
Zusatzlasten führen.
• Fehlender Marktaustritt kann wohlfahrtsfördernde
Selektionseffekte verhindern.
• Markteintritt ist bei hohen Fixkosten im Vergleich zur
Monopollösung effizienzmindernd.
53
If the automobile had followed the same development cycle as the computer,
computer a Rolls-Royce
Rolls Royce would cost
$100 today, get one million miles to the gallon, and explode once a year, killing everyone inside
(Robert X. Cringely, Info World)
2.1.3 Dynamische Ineffizienz
• Entscheidend für Wohlstand und Wachstum sind
Produktivitätssteigerungen und Innovationen.
• Generell werden Firmen nur dann bereit sein, in Forschung und
Entwicklung (F+E) zu investieren, wenn ihnen hinreichend
E
Erträge
aus der
d Innovation
I
i zufließen.
fli ß
• Oft wird
i d argumentiert,
ti t dass
d Monopole
M
l zu träge
t ä sind
i d undd zu
geringe Anreize haben, in F+E zu investieren.
54
2.1.3 Dynamische Ineffizienz
• Auf der anderen Seite machte Schumpeter (1975) bereits darauf
aufmerksam, dass die Rendite der Innovationen in perfekten
Märkten nicht von dem Innovator eingesteckt wird, sondern
wegkonkurriert wird.
• Ist also eine gewisse Monopolmacht Voraussetzung für
Fortschritt weil Firmen im Wettbewerb keine starken
Fortschritt,
Innovationsanreize haben?
• Sind Wettbewerbsmärkte oder Monopole eher zu Innovationen
bereit?
• Wir werden sehen, dass die Antworten auf diese Fragen weniger
kl sind,
klar
i d als
l dies
di manchmal
h l suggeriert
i t wird.
id
55
2.1.3 Dynamische Ineffizienz
• Entscheidend für eine Innovation ist der erwartete Gewinn vor
und nach F+E Investitionen.
g , inwieweit sich Innovationen auszahlen,, hängt
g von
• Die Frage,
der Wettbewerbsform und den Rahmenbedingungen ab.
• Es sei angenommen, dass Innovationen (Fix-) Kosten
verursachen und zu einer Reduktion der (Grenz-) Kosten der
Produktion führen.
führen
• Außerdem nehmen wir der Einfachheit halber an, dass die
inverse Nachfrage durch p(Q) = 1 – Q gegeben ist.
56
2.1.3 Dynamische Ineffizienz
• Im Monopolfall gilt für den Gewinn:
πM
⎛1− c ⎞
=⎜
⎟
⎝ 2 ⎠
2
• D.h. eine marginale Produktivitätserhöhung bringt:
∂π M 1 − c
−
=
∂c
2
57
2.1.3 Dynamische Ineffizienz
• Im
I Cournot-Duopol
C
tD
l gilt
ilt fü
für den
d Gewinn:
G i
π iC =
(1 − 2ci + c j ) 2
9
• D.h.
D h eine marginale Produktivitätserhöhung bringt Firma i:
∂π iC 4(1 − 2ci + c j )
−
=
∂ci
9
4(1 − c)
=
, falls beide mit denselben Kosten c starten.
9
• Kann die Innovation von dem Konkurrenten kopiert werden und
starten beide mit Kosten c, so reduziert sich der marginale
Gewinn aufgrund der Innovation:
∂π iC 2(1 − c )
−
=
58
∂c
9
2.1.3 Dynamische Ineffizienz
• IIm Bertrand-Duopol
B t dD
l machen
h beide
b id Firmen
Fi
ausgehend
h d von
identischen Grenzkosten c Nullgewinne.
• Eine unilaterale Produktivitätserhöhung auf ci < c führt dazu,
dass Firma i im Gleichgewicht die gesamte Nachfrage (1 – c)
bekommt und einen Gewinn in Höhe von (c – ci)(1 – c) macht.
• ((Beii einem
i
Preis
i > c bekommt
b k
dder potenzielle
i ll Konkurrent
k
die
di
Nachfrage; siehe Kapitel 2.2.1.)
• D.h. eine marginale Produktivitätserhöhung bringt Firma i:
∂π iB
−
= 1− c
∂ci
• Kann die Innovation von dem Konkurrenten kopiert werden, so
59
machen beide vor und nach der Innovation Nullgewinne.
2.1.3 Dynamische Ineffizienz
• Al
Also: die
di marginalen
i l Anreize
A i zu ForschungsF
h
undd
Entwicklungstätigkeiten sind kleiner, wenn die Konkurrenten
die Innovation kopieren
p
dürfen und können.
• In diesem Fall ist der Anreiz des Monopolisten, in F+E zu
investieren größer als im Konkurrenzfall.
investieren,
Konkurrenzfall
• Können oder dürfen Innovationen nicht kopiert werden, dann
sind
i d im
i Monopolfall
M
lf ll die
di marginalen
i l Anreize
A i für
fü F+E größer
öß als
l
im Cournot-Fall, aber kleiner als im Bertrand-Fall.
• Dies liegt daran, dass Innovationen im Bertrand-Fall einen
großen Wettbewerbsvorsprung auslösen, während im CournotFall der Innovator nur einen geringen Einfluss auf Preise hat.
hat
• (Die Ergebnisse können sich bei diskreter Betrachtung ändern!)
60
2.1.3 Dynamische Ineffizienz
• Oft wird
i d in
i der
d Literatur
Lit t der
d Aspekt
A kt betont,
b t t dass
d im
i Monopolfall
M
lf ll
der Anreiz fehlt, sich einen Wettbewerbsvorteil zu verschaffen,
und dass daher dort weniger
g Innovationen entstehen.
• Aber: Diese These ist nicht robust, wie wir gesehen haben.
• Auch empirische Untersuchungen zeigen keine eindeutige
Korrelation zwischen Marktstruktur und Innovation.
• Es scheint als ob Innovationen am ehesten in einer „mittleren“
Konkurrenzsituation hervorgebracht werden.
• Denn: Einerseits stimuliert die Konkurrenz die
Innovationstätigkeit von Firmen, und
• andererseits ist die Wahrscheinlichkeit, dass dem Innovator
die Erträge seiner Erfindung zufließen, hinreichend groß.
61
I lik ti
Implikationen
fü
für di
die W
Wettbewerbspolitik
ttb
b litik
• Eine Schlussfolgerung ist aus der Analyse klar: Ohne
Marktmacht kommt es nicht zu Innovationen.
• Sowohl im Monopolfall, als auch im Cournot- und im BertrandFall gelingt es der innovierenden Firma, den Preis profitabel zu
b i fl
beeinflussen
– also
l Marktmacht
k
h auszunutzen.
62
2.1.3 Dynamische Ineffizienz
• Dies verstärkt die Argumentation aus den früheren Kapiteln.
• Monopolistische Marktmacht ist zwar Quelle verschiedener
Ineffizienzen,, aber auch ohne Marktmacht kann Effizienz nicht
hergestellt werden.
• Eine
Ei first-best
fi t b t Situation
Sit ti ist
i t nicht
i ht erreichbar.
i hb
• Insbesondere wird häufigg argumentiert,
g
, dass aufgrund
g
mangelnder Innovationsanreize in wettbewerblichen Märkten
Patentschutz für Innovationen gewährt werden muss.
• (Oder auch Urheberrechte, Markenschutz etc.)
63
2.1.3 Dynamische Ineffizienz
•
Ein Patent gewährt dem Inhaber das Recht, seine Innovation
für einen festgelegten Zeitraum als einziger zu nutzen, so dass
der Innovator zu einem Monopolisten wird.
•
Gesamtwirtschaftlich
G
t i t h ftli h existiert
i ti t hierbei
hi b i ein
i Trade-Off
T d Off zwischen
i h
dem Schutz des Innovators und dem Wohl der Allgemeinheit.
•
Sobald eine Innovation durchgeführt worden ist, ist es eine
wohlfahrtstheoretische Verschwendung, die Nutzung zu
beschränken.
beschränken
•
Besonders klar wird dieses Problem z.B. bei F+E in der
Medizin, wo Patentrechte zuweilen eine Sache von Tod und
Leben sein können ....
64