3. Einkommens- und Substitutionseffekte In diesem Abschnitt soll es

I. Die Theorie des Haushaltes
Mikroökonomie I SS 2003
3. Einkommens- und Substitutionseffekte
aktuelle Version vom 20.05.03
3. Einkommens- und Substitutionseffekte
In diesem Abschnitt soll es darum gehen, im Haushaltsmodell die von Preisänderungen ausgelösten Effekte auf die Güternachfrage näher aufzuschlüsseln. Dabei wird sich insbesondere
zeigen, dass die Normalitätsannahme auch Auswirkungen auf die Richtung von Preiseffekten
bei der Güternachfrage hat. So ergibt sich insbesondere, dass ein normales Gut niemals ein
Giffen-Gut sein kann.
a) Die Zerlegung des Gesamteffekts in Einkommens- und Substitutionseffekt
Wir gehen jetzt von einem etwas anderen Szenario aus als im vorangehenden Kapitel. Und
zwar nehmen wir jetzt an, dass sich (bei konstantem Einkommen y und konstantem Preis p1
von Gut 1) der Preis von Gut 2 (etwa durch eine Mengensteuer mit Steuersatz t ) vom ursprünglichen Wert p2 auf p% 2 ( = p2 + t , wenn t den Mengensteuersatz einer speziellen
Verbrauchsteuer auf Gut 2 bezeichnet) erhöht. Die Budgetgerade dreht sich dann um den
Punkt ( y / p1 ,0) nach unten. Den Optimalpunkt auf der alten Budgetlinie bezeichnen wir mit
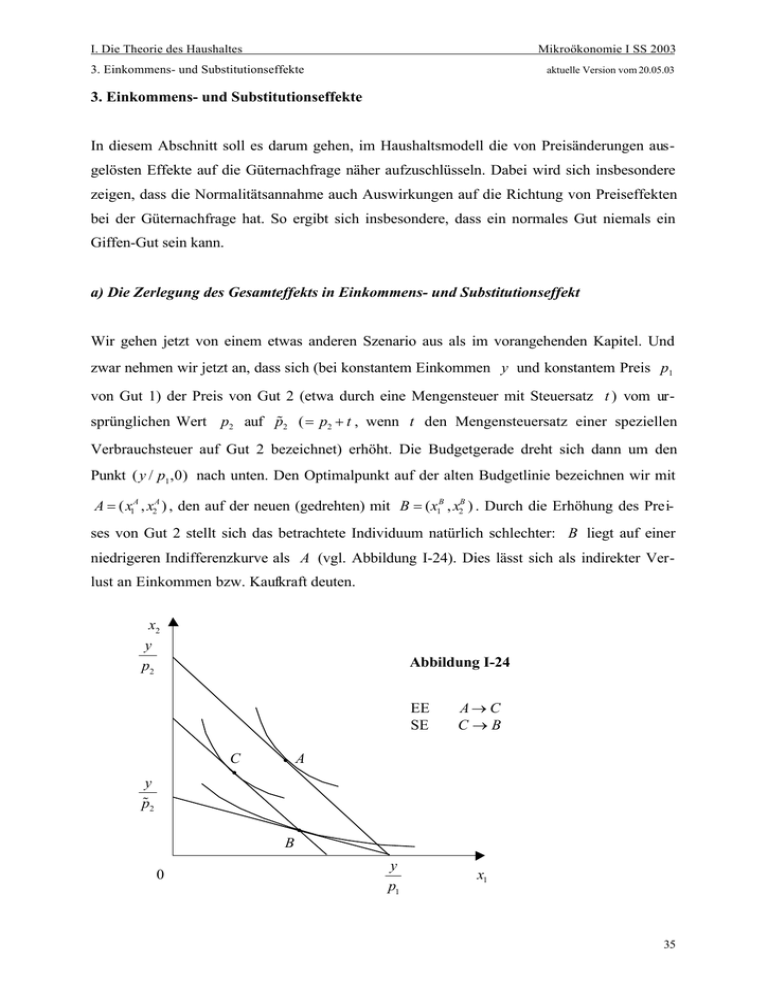
A = ( x1A , x2A ) , den auf der neuen (gedrehten) mit B = ( x1B , x2B ) . Durch die Erhöhung des Preises von Gut 2 stellt sich das betrachtete Individuum natürlich schlechter: B liegt auf einer
niedrigeren Indifferenzkurve als A (vgl. Abbildung I-24). Dies lässt sich als indirekter Verlust an Einkommen bzw. Kaufkraft deuten.
x2
y
p2
Abbildung I-24
EE
SE
C
A→ C
C→B
A
y
p% 2
B
0
y
p1
x1
35
I. Die Theorie des Haushaltes
3. Einkommens- und Substitutionseffekte
Mikroökonomie I SS 2003
aktuelle Version vom 20.05.03
Im steuerpolitischen Kontext wird besonders schnell klar, was hinter dieser Interpretation
steckt: Der eigentliche Zweck der Besteuerung (hier von Gut 2) besteht ja darin, dem Individuum Einkommensteile zu entziehen, mit denen der Staat dann öffentliche Güter bereit stellt.
Der Betrag, den das Individuum im Punkt B an Steuern bezahlt, beträgt tx2B (Steuersatz x
Bemessungsgrundlage) und beschreibt seine Einkommenseinbuße. Wenn man nun den Steuersatz als Differenz zwischen dem neuen und dem alten Preis ausdrückt ( t = %p2 − p2 = ∆p2 ),
kann man den durch die Preiserhöhung bei Gut 2 verursachten impliziten Einkommensverlust
auch wie folgt formulieren:
(I-28)
∆p2 x2B = ( p% 2 − p2 ) x2B .
Wir wollen uns (in einer Art Gedankenexperiment) jetzt überlegen, was geschehen würde,
wenn man dem Individuum diesen Einkommensbetrag direkt (d. h. ohne Veränderung des
relativen Preisverhältnisses von p1 / p2 auf p1 / p% 2 ) entziehen würde. Bei unserer steuerpolitischen Anwendung bedeutet dies, dass die Mengensteuer auf Gut 2 durch eine direkt am Einkommen ansetzende Steuer ersetzt wird, die das gleiche Steueraufkommen erbringen soll.
Grafisch wird diese Überlegung dadurch umgesetzt, dass die ursprüngliche Budgetgerade
parallel nach unten verschoben wird, und zwar (abgelesen an der x2 -Achse) um den Betrag
p% 2 − p2 B
x2 (vgl. Abbildung I-24). Die auf diese Weise verschobene Budgetgerade geht dann
p2
durch Punkt B .
Eine ganz genaue Begründung dieser Aussage kann man auch mit Hilfe der folgenden kleinen Rechnung
geben. Damit ein Punkt ( x1 , x2 ) auf der parallel verschobenen Budgetgeraden liegt, muss er die Bedingung
p1 x1 + p 2 x2 = y − ( p% 2 − p 2 ) x2B
erfüllen. Wenn man auf der linken Seite x1 = x1B und x2 = x2B setzt, ist diese Bedingung äquivalent mit
p1 x1B + p% 2 xB2 = y .
Dies ist aber genau die formale Bedingung dafür, dass B = ( x1B , x2B ) auf der neuen gedrehten Budgetgeraden liegt.
36
I. Die Theorie des Haushaltes
Mikroökonomie I SS 2003
3. Einkommens- und Substitutionseffekte
aktuelle Version vom 20.05.03
Es wird dem Individuum also genau soviel Einkommen entzogen, damit es bei den ursprünglichen Güterpreisen p1 und p2 das Güterbündel ( x1B , x2B ) erwerben könnte und in diesem
Sinne also über die gleiche Kaufkraft verfügt.
Den Optimalpunkt auf der durch diese hypothetische Überlegung bestimmten parallel verschobenen Budgetgeraden bezeichnen wir mit C = ( x1C , x2C ) . Weil diese parallel verschobene
Hilfsbudgetgerade steiler ist als die gedrehte Budgetlinie, liegt C (wegen der Monotonie und
Konvexität der Indifferenzkurven) links oberhalb von B auf einer höheren Indifferenzkurve.
Durch die Konstruktion haben wir erreicht, dass wir den durch die Preiserhöhung bei Gut 2
erzeugten Gesamtnachfrageeffekt A → B in zwei Teileffekte zerlegen können:
-
den Einkommenseffekt (EE) A → C
Er beschreibt die Nachfrageeffekte, die allein vom (durch die Erhöhung des Preises von
Gut 2 indirekt ausgelösten) Kaufkraftverlust verursacht werden, ohne dass sich zugleich
das Preisverhältnis ändert. Wenn beide Güter normal (non-inferior) sind, führt der Einkommenseffekt zu einem Nachfragerückgang bei beiden Gütern. Es gilt also
(I-29)
-
x1C < x1A
und
x2C < x2A .
den Substitutionseffekt (SE) C → B
Hier ist der von der Preiserhöhung bewirkte indirekte Einkommensverlust ausgeschaltet
("heraus destilliert"), so dass allein der - bei konstanter Kaufkraft - von der Änderung der
relativen Preise ausgelöste Nachfrageeffekt bleibt. Es gilt (wie Abbildung I-24 zeigt) bei
gegebener Konvexität der Indifferenzkurve
(I-30)
x1B > x1C
und
x2B < x2C .
Wenn beim Übergang von C nach B (bei unterstellter konstanter Kaufkraft) der Preis
von Gut 2 steigt, wird das Individuum vom teuerer gewordenen Gut 2 weniger und dafür
vom im Preis unveränderten Gut 1 mehr konsumieren. Das Individuum substituiert dann
Gut 2 durch Gut 1. Daher resultiert die Beziehung "Substitutionseffekt".
37
I. Die Theorie des Haushaltes
3. Einkommens- und Substitutionseffekte
Mikroökonomie I SS 2003
aktuelle Version vom 20.05.03
Die hiermit präsentierte Zerlegung des Gesamteffekts in einen Einkommens- und einen Substitutionseffekt erlaubt zwei wichtige Schlussfolgerungen:
1. Schlussfolgerung:
Aus (I-29) und (I-30) folgt x2B < x2A . Wenn der Preis eines normalen Gutes steigt, lässt sich
somit eindeutig feststellen, dass die Nachfrage nach diesem Gut sinken muss. Insbesondere
kann ein normales Gut also (in der zuvor eingeführten Terminologie) kein Giffen-Gut sein.
Im Umkehrschluss ist dann jedes Giffen-Gut notwendigerweise inferior.
Wäre Gut 2 inferior, würde xC2 > x2A gelten. Ist die Differenz x2B − xC2 ( < 0 ) (betragsmäßig) relativ groß,
so kann es durchaus sein, dass x2B − x2A =( x2B − x2C ) +( xC2 − x2A ) doch negativ ist. Ein inferiores Gut muss
also nicht unbedingt ein Giffen-Gut sein. Ein inferiores Gut ist nur dann ein Giffen-Gut, wenn der Einkommenseffekt hinreichend groß ist; überwiegt der Substitutionseffekt dagegen den Einkommenseffekt,
handelt es sich um ein "gewöhnliches" Gut.
Bei Gut 1, dessen Preis unverändert bleiben soll, lässt sich auch bei Normalität über die
Richtung des Gesamteffekts nichts Eindeutiges sagen. Der Einkommenseffekt x1C − x1A ist hier
zwar auch negativ, der Substitutionseffekt x1B − x1C jedoch positiv. Für das Vorzeichen des
Gesamteffekts kommt es also darauf an, welcher der beiden Teileffekte relativ stärker ist.
2. Schlussfolgerung
Dass der Punkt C auf einer höheren Indifferenzkurve als der Punkt B liegt, hat eine bedeutsame steuerpolitische Konsequenz: Bei direktem Einkommensentzug stellt sich das Individuum besser als unter dem Einfluss einer Mengensteuer, ohne dass der Staat bei dem hier
unterstellten Wechsel von einer Mengensteuer auf eine (pauschale) Einkommensteuer auf
Steuereinnahmen verzichten müsste. Umgekehrt: Bei effektiv gleicher Steuerzahlung belastet
die spezielle Mengensteuer (hier auf Gut 2) aufgrund der von ihr verursachten Verzerrung der
relativen Preise das Individuum stärker als eine pauschale Einkommensteuer. In diesem Sinne
erzeugt eine die Preise verzerrende Steuer somit "steuerliche Zusatzlasten" (Excess Burdens).
38
I. Die Theorie des Haushaltes
Mikroökonomie I SS 2003
3. Einkommens- und Substitutionseffekte
aktuelle Version vom 20.05.03
b) Die Slutzky-Gleichung
Mathematisch lässt sich die Unterteilung in Einkommens- und Substitutionseffekt mit Hilfe
der Slutzky-Gleichungen beschreiben. Zu deren formaler Herleitung kürzen wir die Menge nänderung durch Einkommens- und Substitutionseffekt in der folgenden Weise ab:
(I-31)
∆x2E = x2C − x2A
(E A Einkommenseffekt)
(I-32)
∆x2S = xB2 − xC2
(S A Substitutionseffekt)
Für den Gesamteffekt ∆x2 = x2B − x2A gilt dann
(I-33)
∆x2 = ∆x2S + ∆x2E
bzw. nach Division beider Seiten von (I-33) durch ∆p2
(I-34)
∆x2 ∆x2S ∆x2E
=
+
.
∆p2 ∆p2 ∆p2
Der zweite Summand auf der rechten Seite von (I-34) lässt sich weiter in zwei Komponenten
zerlegen, und zwar in die durch ∆p2 verursachte Änderung des effektiven Einkommens
∆y / ∆p2 und die von dieser Einkommensänderung dann ausgelöste Veränderung der Nachfrage ∆x2 / ∆y . Man hat dann
(I-35)
∆x2E ∆x2 ∆y
=
.
∆p2
∆y ∆p2
Über ∆y infolge einer Preisänderung ∆p2 = p%2 − p2 wissen wir aber schon Bescheid. Zuvor
hatten wir ja bereits den Einkommensverlust quantifiziert (s. (I-28)). Es gilt also
(I-36)
∆y = − ( p% 2 − p2 ) x2B =−∆ p 2x 2B .
Insgesamt erhält die Slutzky-Gleichung gemäß (I-34) also die folgende Form
39
I. Die Theorie des Haushaltes
Mikroökonomie I SS 2003
3. Einkommens- und Substitutionseffekte
(I-37)
aktuelle Version vom 20.05.03
∆x2 ∆x2S
∆x
=
− x2B 2 .
∆p2 {
∆p2
∆y
123
SE
EE
Wenn ∆p2 gegen null geht, erhält man als infinitesimale Version der Slutzky-Gleichung
(I-38)
∂x2 ∂x2
∂x
=
− x2 2 .
∂p2 ∂p2 S
∂y
Für das Gut 1 mit dem unveränderten Preis p1 bekommt man ganz analog die SlutzkyGleichung
(I-39)
∆x1 ∆x1S
∆x
=
− x2B 1
∆p2 ∆p2
∆y
bzw. in infinitesimaler Form
(I-40)
∂x1 ∂x1
∂x
=
− x2 1 .
∂p2 ∂p2 S
∂y
(Warum taucht übrigens in den Slutzky-Gleichungen für Gut 1 im zweiten Summanden x2
und nicht x1 auf? Auf den ersten Blick sieht es ja eher wie ein Tippfehler aus!)
40