2. Monopol 2.1 Das klassische Einproduktmonopol

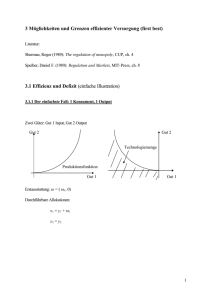
1
2. Monopol
In diesem und den folgenden Kapiteln stehen die Konsequenzen und Grenzen von Marktmacht im
Mittelpunkt. Dabei wird in diesem Kapitel zunächst die einfachste Marktform untersucht, in der
gleichzeitig auch die höchste Ausprägung von Marktmacht auftreten kann: die des Monopols.
Grundsätzlich wird der Preissetzungsspielraum - und damit das Ausmaß von Marktmacht - durch
zwei Faktoren bestimmt. Zum einen ist dieser Spielraum durch das Nachfrageverhalten im Markt
begrenzt, zum anderen durch das Angebot von Substituten durch Konkurrenten. In der
Marktform des Monopols wird davon ausgegangen, daß es solche Rivalen nicht gibt, so daß die
Marktmacht nur durch die Marktnachfrage beschränkt ist.
In der realen Welt sind solchermaßen definierte Monopole so gut wie nie anzutreffen. Zu fast
jedem Gut eines Herstellers findet sich ein Substitut eines anderen Herstellers. Wenn wir uns hier
trotzdem mit dieser Marktform beschäftigen, dann tun wir dies, um zunächst strategische
Interaktionen zwischen konkurrierenden Unternehmen ausklammern zu können. Diese werden in
den folgenden Kapiteln diskutiert. Dabei wird sich herausstellen, daß sich die zentralen
Erkenntnisse in diesem Kapitel mit geringen Modifikationen auf die allgemeine Situation
übertragen lassen.
Wir werden zunächst den Fall eines monopolistischen Einprodukt-Unternehmens betrachten und
dann den Fall eines monopolistischen Mehrprodukt-Unternehmens aufgreifen.
2.1 Das klassische Einproduktmonopol
Der Fall des Einprodukt-Monopols wird meist implizit in einer Welt mit zwei Gütern diskutiert.
Das eine Gut ist das vom Monopolisten hergestellte Gut. Das andere ist ein Numerairegut, das
gleichzeitig als Input in den Produktionsprozeß des Monopols eingeht. Bezeichnet man mit x(p)
die Nachfrage (implizite Annahme quasilinearer Präferenzen!), der sich der Monopolist für sein
Produkt gegenübersieht, wenn er den Preis p fordert, und C(x) die Kosten, wenn er x Einheiten
produziert, dann läßt sich das klassische Preisfindungsproblem des Monopolisten formal
darstellen durch
max px ( p) − C( x ( p)) .
p
In der Darstellung findet man offenbar das Numerairegut nicht mehr explizit. Man beachte jedoch,
daß die Gewinnfunktion
2
Π( p): = px ( p) − C( x( p))
in Einheiten des Numerairegutes ausgedrückt ist.
Die Charakterisierung des gewinnmaximalen Preises ergibt sich aus der Bedingung erster
Ordnung
( p m − C' ( x( p m )))x ' ( p m ) + x ( p m ) = 0 ,
die sich umformen läßt in
p m − C'( x ( p m ))
x( p m)
1
1
=
−
=:
.
m
m
m
p
p
x' ( p ) ε ( p m )
Dabei ist ε(p) die Preiselastizität der Nachfrage. Implizit sind wir davon ausgegangen, daß das
Problem überhaupt eine Lösung besitzt und daß diese positiv ist.
Daraus können wir drei Fakten direkt ablesen: erstens übersteigt der Preis die Grenzkosten,
zweitens wird der Preis so gewählt, daß die Elastizität ε(p) > 1 ist, und drittens weicht der Preis
umso mehr von den Grenzkosten ab, je kleiner die Preiselastizität der Nachfrage ist.
Beispiel: x(p) = p-ε, ε > 1, C(x) = cx
pm − c 1
cε
= ⇔ pm =
m
ε
ε −1
p
[
Die Größe p m − C' (c ( p m ))
]
p m kann als Indikator für die Marktmacht angesehen werden.
Falls der Markt durch vollständige Konkurrenz geprägt wäre, wäre dieser Indikator 0 (Preis =
Grenzkosten). In der Literatur wird dieser Indikator meist Lerner-Index genannt. Für empirische
Zwecke ist es interessant anzumerken, daß bei konstanten Grenzkosten, C(x) = cx, der LernerIndex der Umsatzrendite entspricht:
p − c px − cx
=
.
p
px
Da mit dem Preis über die Nachfragefunktion eindeutig eine Menge festgelegt wird, kann ein
Monopolist auch direkt die Menge festlegen. Der Preis ergibt sich dann aus der PreisAbsatzfunktion p(.).
Wählt er die Menge als Entscheidungsvariable, so löst er das Problem
3
max p( x ) x − C( x) ,
x
was zu der Bedingung erster Ordnung
MR ( x m ): = p' ( x m ) x m + p( x m ) = C'( x m )
führt, wobei MR(x) den Grenzerlös bei der Menge x bezeichnet. Arrangiert man diese Gleichung
um
p( x m ) − C' ( x m )
xm
m
=
−
p
'(
x
)
p (x m )
p (x m )
so erkennt man, daß diese Bedingung wegen p' ( x m) = 1/x'(p(x m)) mit der für den
monopolistischen Preis übereinstimmt: pm = p(x m). Wir können bei Entscheidungsproblemen
damit frei zwischen den Variablen Preis und Menge wählen. Das Ergebnis ist stets dasselbe.
Kommen wir nun zur Bewertung dieser Preissetzung. Da der Monopolpreis die Grenzkosten
übersteigt, ist die resultierende Allokation nicht Pareto-optimal. Konsumenten sind bereit, für eine
weitere Einheit des Gutes mehr als die entstehenden Kosten zu zahlen. Sie würden sich durch eine
Ausdehnung der Produktion also besser stellen. Eine solche Ausdehnung dominiert daher die
Monopolallokation.
Mit Hilfe des sozialen Überschusses lassen sich diese Allokationsverluste verdeutlichen. Bei
vollständigem Wettbewerb würde sich der Preis einspielen, bei dem die Nachfragekurve die
Grenzkostenkurve schneidet
p c = C '( x ( p c ))
oder in Mengen ausgedrückt:
p( x c ) = C' ( x c ) ,
wobei p(.) wieder die inverse Nachfragefunktion oder Preis-Absatzfunktion ist. Der
Monopolpreis pm liegt über pc. Nehmen wir nämlich an, daß pm ≤ pc gilt, dann folgt unter unseren
Annahmen x(pm) ≥ x(pc) und bei nicht fallenden Grenzkosten und endlicher Elastizität der
Nachfrage bzgl. des Preises
pm > C'(x(pm)) ≥ C'(x(pc)) = pc.
4
Damit ist die Annahme zum Widerspruch geführt. Daher ist der soziale Überschuß, der mit dem
pc nach pm verbunden ist,
pc
m
c
∫pm x ( p)dp + Π (p ) - Π (p )
oder in Mengen ausgedrückt
xm
m
c
∫xc p( x )dx - ( C(x ) - C(x ) )
p
p(.)
m
p
C'(.)
c
p
xm
xc
x
Das Integral ist in beiden Fällen negativ, da die obere Grenze unter der unteren liegt. Die
schraffierte Fläche entspricht dem sozialen Überschuß, der sich hier negativ und somit als sozialer
Verlust erweist.
Dies ist der zentrale Grund für die Ablehnung von Marktmacht aus sozialer Sicht. Man beachte,
daß das Schlimmste an dem überhöhten monopolistischen Preis nicht die erhöhten Ausgaben für
die Konsumenten sind. Diese bedeuten nur Transfers zwischen den Konsumenten und den
Eigentümern des monopolistischen Unternehmens. Das Maß des sozialen Überschusses ist
jedoch, wie in Kapitel 1 gesehen, in bezug auf Einkommensumverteilungen invariant. Die kritische
Eigenschaft ist die Einschränkung der Produktion. Es kommen einige Konsumenten nicht in dem
Maße in den Genuß des Gutes, das aus sozialer Sicht wünschenswert wäre.
Literatur:
Tirole, Jean (1988): The Theory of Industrial Organization, MIT-Press, Kapitel 1.1.1