3.1 Effizienz und Defizit

3 Möglichkeiten und Grenzen effizienter Versorgung (first best)
Literatur:
Sherman, Roger (1989): The regulation of monopoly, CUP, ch. 4
Spulber, Daniel F. (1989): Regulation and Markets, MIT-Press, ch. 8
3.1 Effizienz und Defizit (einfache Illustration)
3.1.1 Der einfachste Fall: 1 Konsument, 1 Output
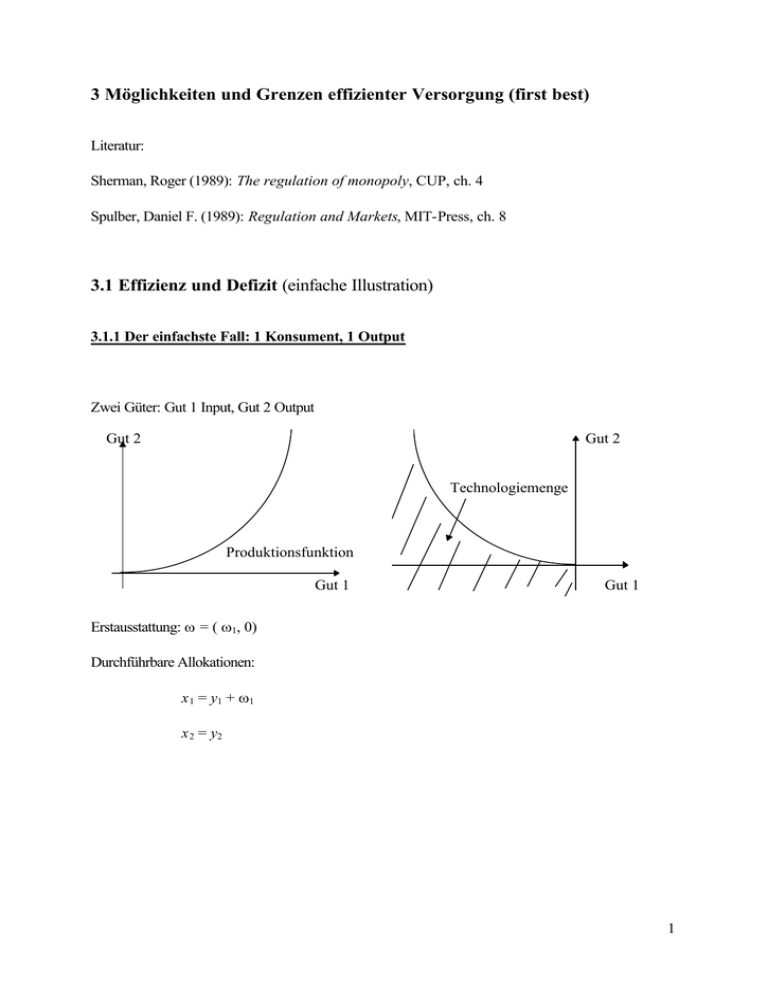
Zwei Güter: Gut 1 Input, Gut 2 Output
Gut 2
Gut 2
Technologiemenge
Produktionsfunktion
Gut 1
Gut 1
Erstausstattung: ω = ( ω1, 0)
Durchführbare Allokationen:
x 1 = y1 + ω1
x 2 = y2
1
Gut 2
Y + {ω}
ω1
Gut 2
Gut 1
Gut 2
x2 *
Indifferenzkurve
Indifferenzkurve
ω1
x1 *
ω1
Gut 1
Gut 1
Steigung der "Transformationskurve" = Kehrwert der Grenkosten
Gut 2
x2 *
Indifferenzkurve
x1 *
p1
1
=
p2 MC( x2* )
m
ω1
Gut 1
Gut 1 als Numerairegut: p2 = MC(x 2*)
m = x1* + p2 x 2* = ω 1 + y1* + p2 y *2
⇒ Steuer ω1 - m
2
Gut 2
y2*
Maßnahmen zur Durchführung der Paretoeffizienten Allokation
1. p2 = MC(x 2*)
2. Steuer ω1 - m = Subvention an Unternehmen
3. Verpflichtung des Unternehmens, x 2* zu produzieren
Spezialfall Fixkosten und konstante Grenzkosten:
Gut 2
Gut 2
1
c = MC
F
Gut 1
Gut 1
Gut 2
ω1
Gut 1
p2 = c Steuer = F
3
Dieselbe Analyse mit sozialem Überschuß
Annahme: quasilineare Präferenzen
u ( x1 , x 2 ) = x1 + v( x 2 )
Nutzen bei durchführbarer Allokation
u( ω 1 − C ( y ), y) = ω 1 − C ( y ) + v ( y )
y
y
v ( y ) − v( 0) = ∫ v ′ ( x ) dx = ∫ p( x) dx
0
0
Sozialer Überschuß u( x1 , x2 ) − u( ω 1 ,0)
y
=
∫ p( x )dx − C ( y )
0
y
=
∫ p( x )dx − p( y) y
0 44
1
42444
3
+
p( y) y − C ( y )
14
4244
3
Produzentenrente
Konsumentenrente
Preis
Nachfrage
Grenzkosten
maximaler sozialer Überschuß
4
3.1.2 Mehrere Konsumenten
Botschaft: Es gibt nicht die effiziente Outputmenge
Illustration: 2 Konsumenten, 2 Güter, 1 Output, 1 Input
Kosten: C(y) = F + cy
Erstausstattung: (w, 0)
mögliche Allokationen: x A + x B = w − F − c( y A + y B )
Nutzen:
u A ( x A , y A ), u B ( x B , y B )
Innere Lösungen vorausgesetzt: Allokation ist Pareto-effizient, wenn sie folgendes Problem löst:
B
A
B
A
B
A
B
B
B
max u ( w − x − F − c ( y + y ), y ) u.d.N u ( x , y ) ≥ u ( µ)
y A, y B , x B
Bedingung erster Ordnung:
∂
:
∂y A
∂u A
∂u A
( −c) + A = 0
∂x A
∂y
∂
:
∂y B
∂u A
∂
:
∂x B
∂u A
∂x A
∂x A
(−c ) + µ
(−1) + µ
∂u B
∂y B
∂u B
∂x B
=0
=0
zusammenfassen zu:
∂u A
∂y A
∂u
∂x A
A
∂u B
=c =
∂y B
∂u
∂x B
B
Bedingung für Pareto-effiziente Versorgung.
B
Durch Variation von u erhält man alle Pareto-effizienten Allokationen.
5
Beispiel:
u A ( x, y ) = x α y1−α , u B ( x, y ) = x β y 1−β , α < β
Definiere
S := β /(1 − β ), T := α /(1 − α )
Resultat für Pareto-effiziente Outputniveaus:
w− F
w− F
≤y≤
c( S + 1)
c(T + 1)
Ende Beispiel.
Wie läßt sich eine solche Allokation über Preise implementieren?
1.
p=c
(Preis = Grenzkosten)
2.
Deckung des Defizits durch Kopfsteuern
Kopfsubventionen ( E A , E B )
Es gilt dann E A + E B = F. Dabei kann E A oder E B negativ (Subvention) sein.
Dies ist verallgemeinerbar auf viele Konsumenten und Outputs.
6
3.1.3 Direkte Modellierung über Preise
Vereinfachend: 1 Konsument, verallgemeinernd: 2 Outputs
Erstausstattung: (w, 0, 0)
Gut 1: Inputgut = Numerairegut
Budget des Konsumenten: p1 y1 + p 2 y 2 + x ≤ w − E
E ist Steuer, die U als Subvention bekommt.
Nutzen u ( x , y1 , y 2 )
Nachfrageverhalten:
max u( x, y1 , y 2 ) u.d . N. p1 y1 + p 2 y 2 + x ≤ w − E
x, y1, y2
Nachfragefunktionen:
yi ( p1 , p2 , w − E )
Indirekte Nutzenfunktion:
V ( p1 , p 2 , w − E )
Pareto-Effizienz:
max V ( p1 , p 2 , w − E ) u.d.N. E + p1 y1 (⋅) + p 2 y 2 (⋅) − C ( y1 (⋅), y 2 (⋅) ) ≥ 0
p1, p2 , E
Lagrangefunktion:
V ( p1 , p 2 , w − E ) + λ[ E + p1 y1 (⋅) + p 2 y 2 (⋅) − C ( y1 (⋅), y 2 (⋅) ) ]
Bedingungen erster Ordnung:
(1)
(2)
(3)

∂
∂V
∂C ∂y1
∂C ∂y 2 

:0 =
+ λy1 + λ ( p1 −
)
+ ( p2 −
)
∂p1
∂p1
∂y1 ∂p1
∂y 2 ∂p1 


∂
∂V
∂C ∂y1
∂C ∂y 2 

:0 =
+ λy 2 + λ ( p1 −
)
+ ( p2 −
)
∂p 2
∂p2
∂
y
∂
p
∂
y
∂
p

1
2
2
2 

∂
∂V
∂C ∂y1
∂C ∂y 2 

:0 = −
+ λ − λ ( p1 −
)
+ ( p2 −
)
∂E
∂m
∂y1 ∂m
∂y 2 ∂m 

Nutzt man in (1) und (2) die Roy'sche Identität und multipliziert man (3) mit y1, so wird aus (1):
7
(1') 0 = −

∂V
∂C ∂y1
∂C ∂y 2 

y1 + λy1 + λ ( p1 −
)
+ ( p2 −
)
∂m
∂y1 ∂p1
∂y2 ∂p1 

und aus (3):
(3') 0 = −

∂V
∂C ∂y1
∂C ∂y 2 
y1 + λy1 − λ ( p1 −
)
y1 + ( p 2 −
)
y 
∂m
∂y1 ∂m
∂y2 ∂m 1 

(1') – (3') impliziert, wobei λ>0 wegen (3) ausgenutzt ist:

∂C  ∂y1 ∂y1  
∂C  ∂y 2 ∂y 2 


(1'')  p1 −
+
y1  +  p 2 −
+
y =0
∂y1  ∂p1 ∂m  
∂y 2  ∂p1 ∂m 1 

Für die Ableitung nach p2 ergibt sich analog:

∂C  ∂y1 ∂y1  
∂C

(2'')  p1 −
+
y 2  +  p2 −
∂y1  ∂p 2 ∂m  
∂y2

 ∂y 2 ∂y 2 

+
y 2  = 0
 ∂p 2 ∂m 
Nutzt man die Slutsky-Gleichung und bezeichnet mit hi die entsprechenden Hicks'schen
Nachfragefunktionen, dann läßt sich (1'') und (2'') schreiben als
∂C 
 ∂h1 ∂h2 

 p1 −
 0 
∂y1   
 ∂p1 ∂p1 
= 
 ∂h ∂h 
∂C   
1
2

 p 2 −
 0
∂y 2   
 ∂p2 ∂p 2 
Lineare Algebra ==> p i =
∂C
falls
∂yi
 ∂h1 ∂h2 


∂p1 ∂p1 

det 
=: ∆ ≠ 0
∂h1 ∂h2 


∂
p
∂
p
 2 2
Fazit: Preis = Grenzkosten für alle Outputs
8