5 1 6 3 9 8 2 4 7 Suchbäume

Logik und Diskrete Strukturen
Prof. Dr. Ulrich Hertrampf
Einheit 47
Suchbäume
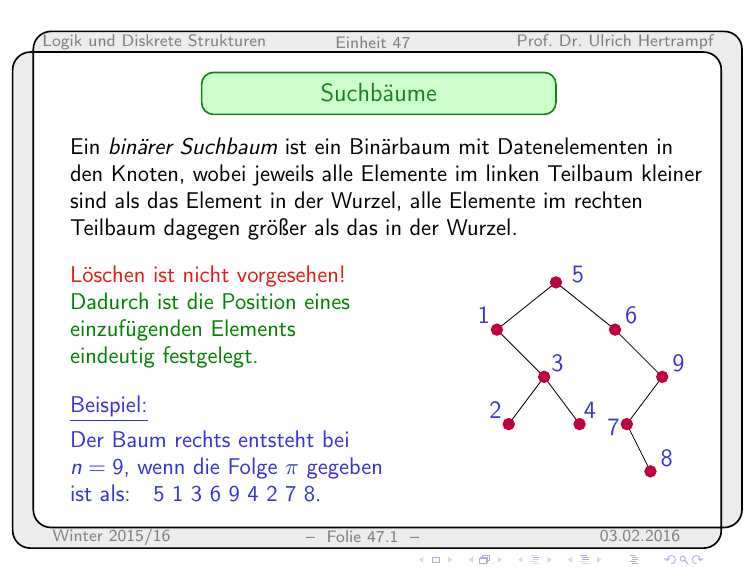
Ein binärer Suchbaum ist ein Binärbaum mit Datenelementen in
den Knoten, wobei jeweils alle Elemente im linken Teilbaum kleiner
sind als das Element in der Wurzel, alle Elemente im rechten
Teilbaum dagegen größer als das in der Wurzel.
Löschen ist nicht vorgesehen!
Dadurch ist die Position eines
einzufügenden Elements
eindeutig festgelegt.
Beispiel:
1
– Folie 47.1 –
6
3
2
Der Baum rechts entsteht bei
n = 9, wenn die Folge π gegeben
ist als: 5 1 3 6 9 4 2 7 8.
Winter 2015/16
5
9
4
7
8
03.02.2016
Logik und Diskrete Strukturen
Prof. Dr. Ulrich Hertrampf
Einheit 47
Die Suchbäume B(π) und BI (π)
Der Suchbaum, der bei der Eingabe π entsteht, heißt B(π).
Es ist aber auch nützlich, einen Baum zu definieren, der entsteht,
wenn nur eine Teilmenge der Eingabe eingefügt wird. Den Baum
zur Teilmenge I bezeichnen wir mit BI (π).
5
3
1
9
3
2
6
7
8
Das ist BI (π) für I = {1, 3, 5, 7, 9}
Und hier ist B{2,3,6,8} (π)
Im folgenden interessieren wir uns dafür, mit welcher Tiefe wir
bei einem solchen Suchbaum rechnen müssen; denn die Tiefe
ist entscheidend für den Zeitaufwand, den man im worst-case
zum Auffinden eines Elements investieren muss.
Winter 2015/16
– Folie 47.2 –
03.02.2016
Logik und Diskrete Strukturen
Einheit 47
Prof. Dr. Ulrich Hertrampf
Mittlere Höhe von Suchbäumen
Wir werden drei Zufallsvariablen benutzen; dabei ist unser
Wahrscheinlichkeitsraum die Menge aller Permutationen der
Zahlen {1, . . . , n}. Die Permutationen seien gleichverteilt.
Die drei Zufallsvariablen sind:
Ri (π) = „Wurzel von B(π) ist i“ ∈ {0, 1}
XI (π) = „Höhe von BI (π)“
∈ {0, . . . , n − 1}
YI (π) = 2XI (π)
Wir setzen Xn = X{1,...,n} und Yn = Y{1,...,n} und berechnen
zunächst E [Yn ] und daraus dann E [Xn ].
Zu diesem Zweck zeigen wir erst, dass E [Yn ] ∈ O(n3 ) gilt.
Winter 2015/16
– Folie 47.3 –
03.02.2016
Logik und Diskrete Strukturen
Einheit 47
Prof. Dr. Ulrich Hertrampf
E [Yn ] ∈ O(n3 )
Offenbar ist E [Y1 ] = 1, wir setzen jetzt also n ≥ 2 voraus.
Für jedes π : {1, . . . , n} → {1, . . . , n} gilt
Yn (π) = 2 ·
Damit folgt:
n
P
Ri (π) · max{Y{1,...,i−1} , Y{i+1,...,n} }
i=1
Der Faktor zwei kommt von der Erhöhung um 1 bei Xn .
E [Yn ] = 2 ·
n
P
E [Ri · max{Yi−1 , Yn−i }
i=1
denn Ri (π) = 0, falls π(1) 6= i; es wird also nur der Fall mit i als
Wurzel des Baums im jeweiligen Summanden berechnet. Der linke
Teilbaum enthält dann {1, . . . , i − 1}, der rechte {i + 1, . . . , n}.
Da aber die mittlere Höhe des Baums nicht von der Bezeichnung der Eingabezahlen
abhängen kann, muss Y{i +1,...,n} mit dem gleichen Wert zum erwarteten Mittel
beitragen wie Yn−i .
Winter 2015/16
– Folie 47.4 –
03.02.2016
Logik und Diskrete Strukturen
Einheit 47
Prof. Dr. Ulrich Hertrampf
Ausrechnen
Die Zufallsvariable Ri ist sowohl von Y{1,...,i−1} als auch von
Y{i+1,...,n} unabhängig, daher ist der Erwartungswert des Produkts
hier gleich dem Produkt der Erwartungswerte, d.h.
E [Yn ] = 2 ·
≤ 2·
=
4
n
·
n
P
i=1
n
P
i=1
n
P
E [Ri ] · E [max{Yi−1 , Yn−i }]
1
n
· (E [Yi−1 ] + E [Yn−i ])
n−1
P
E [Yi ]
E [Yi−1 ] = n4 ·
i=0
i=1
1 n+3
Hieraus folgt E [Yn ] ≤ 4 3 , wie man induktiv leicht sieht.
Der Induktionsanfang für n = 1 ist klar. Nun der Induktionsschritt:
n−1
n−1
P
P i+3 1 n+3 1 n+3
E [Yn ] ≤ n4
E [Yi ] ≤ n1
=n 4 =4 3
3
i=0
i=0
Winter 2015/16
– Folie 47.5 –
03.02.2016
Logik und Diskrete Strukturen
Prof. Dr. Ulrich Hertrampf
Einheit 47
Abschluss des Beweises
Wir haben gezeigt, dass E [Yn ] ≤
1 n+3
4 3
, also E [Yn ] ∈ O(n3 ).
Da die Funktion x 7→ 2x eine konvexe Funktion ist, gilt nach der
Jensen’schen Ungleichung:
2E [Xn ] ≤ E [2Xn ] = E [Yn ] ∈ O(n3 ).
und daher ist E [Xn ] im wesentlichen beschränkt durch 3 log2 n.
Satz:
E [Xn ] ∈ O(log n)
Das bedeutet: Binäre Suchbäume sind im Mittel praktisch so gut
wie im best-case. Besser als logarithmische Tiefe geht nicht!
Winter 2015/16
– Folie 47.6 –
03.02.2016