Die Herbrand

Logik und Diskrete Strukturen
Einheit 23
Prof. Dr. Ulrich Hertrampf
Die Herbrand-Expansion
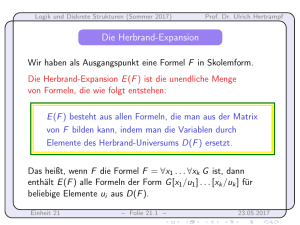
Wir haben als Ausgangspunkt eine Formel F in Skolemform.
Die Herbrand-Expansion E (F ) ist die unendliche Menge
von Formeln, die wie folgt entstehen:
E (F ) besteht aus allen Formeln, die man aus der Matrix
von F bilden kann, indem man die Variablen durch
Elemente des Herbrand-Universums D(F ) ersetzt.
Das heißt, wenn F die Formel F = ∀x1 . . . ∀xk G ist, dann
enthält E (F ) alle Formeln der Form G [x1 /u1 ] . . . [xk /uk ] für
beliebige Elemente ui aus D(F ).
Winter 2015/16
– Folie 23.1 –
02.12.2015
Logik und Diskrete Strukturen
Prof. Dr. Ulrich Hertrampf
Einheit 23
Beispiel
Als Beispiel betrachten wir die Formel
F = ∀x∀y ∀z P(x, f (y ), g (z, x))
Dann ist D(F ) = {a, f (a), g (a, a), f (f (a)), f (g (a, a)), . . . }
und wir erhalten u.a. folgende Elemente von E (F ):
P(a, f (a), g (a, a))
P(a, f (f (a)), g (a, a))
P(f (a), f (a), g (a, f (a)))
P(a, f (a), g (f (a), a))
P(g (f (a), f (a)), f (g (a, a)), g (a, g (f (a), f (a))))
Dagegen gehört P(f (a), f (a), g (a, a)) nicht zu E (F ).
Bitte überlegen Sie sich selbst, warum nicht...
Winter 2015/16
– Folie 23.2 –
02.12.2015
Logik und Diskrete Strukturen
Einheit 23
Prof. Dr. Ulrich Hertrampf
Satz von Gödel, Herbrand, Skolem
Der Satz von Gödel, Herbrand und Skolem führt das Erfüllbarkeitsproblem der Prädikatenlogik auf den aussagenlogischen
Fall zurück – allerdings wird bei der Reduktion die eine
Formel F zu der unendlichen Formelmenge E (F ):
Satz: Eine Skolemformel F ist genau dann erfüllbar,
wenn die Menge E (F ) als aussagenlogische
Formelmenge erfüllbar ist.
Zum Beweis genügt es zu zeigen, dass F genau dann ein
Herbrand-Modell hat, wenn E (F ) erfüllbar ist.
Winter 2015/16
– Folie 23.3 –
02.12.2015
Logik und Diskrete Strukturen
Einheit 23
Prof. Dr. Ulrich Hertrampf
Beweis des Satzes
Die Skolemformel sei F = ∀y1 ∀y2 . . . ∀yn G .
Dann gilt:
A ist Herbrand-Modell für F
⇐⇒
für alle t1 , t2 , . . . , tn ∈ D(F ) gilt
A[y1 /t1 ][y2 /t2 ]...[yn /tn ] (G ) = 1
⇐⇒
für alle t1 , t2 , . . . , tn ∈ D(F ) gilt
(Hier wird Übung 58
- Einheit 20 - benutzt)
A(G [y1 /t1 ][y2 /t2 ] . . . [yn /tn ]) = 1
⇐⇒
für alle H ∈ E (F ) gilt A(H) = 1
⇐⇒
A ist Modell für E (F ).
Winter 2015/16
– Folie 23.4 –
02.12.2015
Logik und Diskrete Strukturen
Einheit 23
Prof. Dr. Ulrich Hertrampf
Satz von Herbrand
Aus dem Satz von Gödel, Herbrand, Skolem folgt direkt der
folgende Satz (Satz von Herbrand):
Satz: Eine Skolemformel F ist genau dann unerfüllbar,
wenn eine endliche unerfüllbare Teilmenge
von E (F ) existiert.
Beweis:
F unerfüllbar
⇐⇒
E (F ) unerfüllbar
⇐⇒
E (F ) hat endliche unerfüllbare
Teilmenge
Die erste Äquivalenz ist der Satz von Gödel, Herbrand, Skolem, die zweite
Äquivalenz folgt aus dem Endlichkeitssatz.
Winter 2015/16
– Folie 23.5 –
02.12.2015
Logik und Diskrete Strukturen
Einheit 23
Prof. Dr. Ulrich Hertrampf
Bemerkungen
• Die Menge E (F ) ist eine Formelmenge der Aussagenlogik!
• E (F ) ist rekursiv aufzählbar.
• Der Satz von Herbrand führt daher zu einem Algorithmus, der
unerfüllbare Formeln in endlicher Zeit erkennt.
• Dieser Algorithmus von Gilmore (sh. Buch) kann aber nicht in
endlicher Zeit erkennen, wenn die Eingabe erfüllbar ist.
Also ist das Unerfüllbarkeitsproblem für
prädikatenlogische Formeln semi-entscheidbar.
Ebenso ist das Gültigkeitsproblem für
prädikatenlogische Formeln semi-entscheidbar.
Winter 2015/16
– Folie 23.6 –
02.12.2015