∑ ) = ( ) Aufgabe 1
Werbung

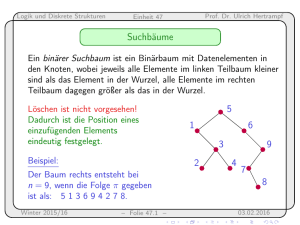
Logik und Diskrete Strukturen Prof. Dr. Ulrich Hertrampf Einheit 50 Aufgabe 1 Wir wollen die Aussage beweisen, die wir in Einheit 47 benutzt haben, um die Tiefe binärer Suchbäume abzuschätzen: n−1 P i=0 Lösung: i+3 3 = n+3 4 Die rechte Seite gibt an, wieviele vier-elementige Teilmengen eine (n + 3)-elementige Menge hat. Dieselbe Anzahl können wir auch so bestimmen: Wir wählen zuerst das größte Element (bzgl. einer beliebigen Anordnung) und dann noch 3 der kleineren Elemente. Für das größte Element kommt das Element i + 4 (für 0 ≤ i ≤ n − 1) in Frage, dann müssen noch drei der i + 3 kleineren Elemente ausgewählt werden. Winter 2015/16 – Folie 50.1 – 04.02.2016 Logik und Diskrete Strukturen Einheit 50 Prof. Dr. Ulrich Hertrampf Das Ziegenproblem Ein Moderator zeigt einem Kandidaten drei Türen, hinter denen ein wertvoller Preis und zwei Trostpreise (die Ziegen) verborgen sind. Der Kandidat darf eine Tür wählen. Hat er eine gewählt, öffnet der Moderator eine der anderen Türen, hinter der sich ein Trostpreis befindet. Nun bietet der Moderator an, der Kandidat darf seine Wahl nochmal ändern. Mit welcher Wahrscheinlichkeit wird der Kandidat gewinnen, wenn er sich „optimal“ verhält? Dieses Problem hat viele Facetten. Wir werden diese in der Vorlesung ausführlich diskutieren. Winter 2015/16 – Folie 50.2 – 04.02.2016 Logik und Diskrete Strukturen Einheit 50 Prof. Dr. Ulrich Hertrampf Carcassone Im Spiel Carcassone gibt es quadratische Karten, deren vier Seiten immer einer Straße (s), einer Stadt (b) oder einer Wiese (w ) entsprechen. Wie viele verschiedene Muster gibt es hier maximal? Lösung: Wir haben drei „uniforme“ Muster. Wieviele Muster mit einer dreifach vorkommenden Seite gibt es? Wieviele Muster mit zwei mal zwei vorkommenden Seiten gibt es? Wieviele Muster, in denen alle drei Typen vorkommen, gibt es? Jetzt noch zusammenzählen... Winter 2015/16 – Folie 50.3 – 04.02.2016 Logik und Diskrete Strukturen Einheit 50 Prof. Dr. Ulrich Hertrampf Nichtkommutative Summen Wieviele Möglichkeiten gibt es, die Zahl s als Summe von n positiven Zahlen zu schreiben, wenn wir ohne das Kommutativgesetz rechnen? Beispiel. Für s = 5 und n = 3 erhalten wir 6, wie man hier sieht: 5 = 3+1+1 = 1+3+1 = 1+1+3 = 2+2+1 = 2+1+2 = 1+2+2 Finden Sie eine einfache Formel für die gesuchte Anzahl? Winter 2015/16 – Folie 50.4 – 04.02.2016 Logik und Diskrete Strukturen Einheit 50 Prof. Dr. Ulrich Hertrampf Schlümpfe Im Buch von Diekert, Kufleitner und Rosenberger finden Sie eine hochinteressante Schlumpf-Aufgabe. Sie hat die Nummer 4.10 und ist zu lang, um sie heute hier zu bearbeiten. Bitte schauen Sie auf Seite 94 im Buch nach und versuchen Sie, die Aufgabe zu lösen, ohne sich zuvor die Lösung im Anhang anzusehen! Winter 2015/16 – Folie 50.5 – 04.02.2016 Logik und Diskrete Strukturen Einheit 50 Prof. Dr. Ulrich Hertrampf Ende Damit sind wir am Ende der Vorlesung Logik und Diskrete Strukturen angelangt. Ich bedanke mich für Ihre Aufmerksamkeit und Disziplin und freue mich darauf, die meisten von Ihnen im nächsten Semester im zweiten Teil des Moduls über die Theoretischen Grundlagen der Informatik mit dem Titel Formale Sprachen und Automatentheorie wiederzusehen. Winter 2015/16 – Folie 50.6 – 04.02.2016