KAPITEL IV DREHBEWEGUNGEN STARRER KÖRPER

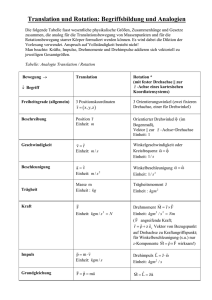
KAPITEL IV
DREHBEWEGUNGEN
STARRER KÖRPER
1. GRUNDBEGRIFFE
1.1 MODELL "STARRER KÖRPER"
Bisher haben wir uns mit der Mechanik der Punktmassen beschäftigt; dabei meinen wir
eigentlich nur die Bewegung des Massenmittelpunktes. Besonders bei technischen
Anwendungen ist es aber oft wichtig, auch Ausdehnung und Gestalt der Körper zu
berücksichtigen. Weil man dabei die Verformungen oft vernachlässigen kann, hat man das
Modell des starren Körpers geschaffen. Er ist wie folgt definiert :
Unter einem starren Körper versteht man ein Gebilde, dessen Ausdehnung und Gestalt sich
nicht verändert.
Jeder starre Körper kann man sich aus unendlich vielen Punktmassen zusammengesetzt
denken. Es müssen sich daher seine Bewegungsgleichungen mit Hilfe der Mechanik der
Punktmassen herleiten lassen.
1.2 TRANSLATION UND ROTATION
Ein starrer Körper führt im Allgemeinen eine Translationsbewegung und eine Rotationsbewegung aus.
Eine Translationsbewegung liegt vor, wenn der starre Körper bei seiner Bewegung die
räumliche Orientierung relativ zu einem Inertialsystem beibehält.
Im Folgenden werden wir nur Translationsbewegungen betrachten, bei denen sich der starre
Körper längs einer Ebene verschiebt. die Bahnen der einzelnen Punktmassen sind dann
kongruente Kurven, die in der gleichen Weise durchlaufen werden.
Eine Rotationsbewegung liegt vor, wenn sich der starre Körper um einen festen Punkt
relativ zu einem Inertialsystem dreht.
In folgendem werden wir nur Rotationsbewegungen betrachten, bei denen sich der starre
Körper um eine feste Achse dreht. Die Bahnen der einzelnen Punktmassen sind dann
konzentrische Kreise, deren Mittelpunkte auf der festen Drehachse liegen. Dabei durchlaufen
die Punktmassen die Bahnen mit unterschiedlicher Geschwindigkeit.
1.3 VEKTORIELLES UND SKALARES PRODUKT ZWEIER VEKTOREN
a) Skalares Produkt
r
r
Beim skalaren Produkt zweier Vektoren v1 und v2 ist das Produkt ein Skalar u .
r r
u = v1 • v2
Der Skalar u ist eindeutig durch seinen Betrag definiert :
r
r
u = v1 ⋅ v2 ⋅ cos α
α ist der Winkel zwischen v1 und v2
STARRE KÖRPER 2
b) Vektorielles Produkt
r
r
Beim vektoriellen Produkt zweier Vektoren v1 und v2 ist das Produkt ein Vektor
r
r r
v = v1 × v2
r
Der Vektor v ist eindeutig definiert durch seinen Betrag und seine Richtung :
r
v
= v1 ⋅ v2 ⋅ sin α
α ist der Winkel zwischen
• Betrag v ⇒ v =
r
v.
r
r
v1 und v2
r r
• Richtung ⇒ Die Wirkungslinie steht senkrecht zur Ebene (v1 , v2 ) .
Der Richtungssinn ergibt sich aus der Regel des rechtsdrehenden
r
Korkenziehers. Drehen wir den 1. Vektor v1 auf kürzestem Weg auf
r
den 2. Vektor v2 , so schreitet der rechtsdrehende Korkenzieher in
r
die positive Richtung des Produktvektors v vor.
Die Reihenfolge der Vektoren im vektoriellen Produkt spielt eine
r r
r r
Rolle. Die vektoriellen Produkte v1 × v2 und v2 × v1 haben zwar den
gleichen Betrag und die gleiche Wirkungslinie aber unterschiedlichen
Richtungssinn.
1.4 DREHMOMENT
Der bereits in der 10. Klasse für den speziellen Fall des Hebels entwickelte Begriff des
Drehmomentes soll jetzt verallgemeinert werden. Wir betrachten dazu einen starren Körper,
der um eine feste Achse,
die Drehachse, drehbar sein soll. An diesem Körper greift im
r
Punkte A eine Kraft F ein, die in einer zur Drehachse senkrecht verlaufenden Ebene liegt.
Diese Kraft bewirkt eine Dreh- oder Rotationsbewegung des Körpers.
Das Drehmoment M ist definiert als das Produkt
aus der Kraft F und dem senkrechten Abstand d
ihrer Wirkungslinie von der Drehachse. Sei r die
Entfernung des Angriffspunktes der Kraft von der
Drehachse so gilt :
M
=
d⋅ f
=
=
r ⋅ sin ϕ ⋅ F
r ⋅ F ⋅ sin ϕ
M
r
r r
Dies ist der Betrag des vektoriellen Produktes M = r × F .
r
r
Unter dem Drehmoment M einer Kraft F , die in einer zur Drehachse senkrechten Ebene
liegt, versteht man das vektorielle Produkt aus dem von der Drehachse zum Angriffspunkt
r
r
der Kraft weisenden Vektor r und der Kraft F .
r
r r
M
=
r×F
Für den Betrag des Drehmomentes gilt
M =
r ⋅ F ⋅ sin ϕ .
Die Richtung des Drehmomentes ist gegeben durch die Regel des rechtsdrehenden Korkenziehers.
STARRE KÖRPER 3
1.5 Winkelgschwindigkeit
Die Winkelgeschwindigkeit ω gibt den Winkel (in rad) an, um den sich der starre Körper in
einer Sekunde dreht.
Bei der gleichförmigen Kreisbewegung ist der Betrag der Winkelgeschwindigkeit ω
konstant. Es gilt dann :
ω
Δϕ
Δt
=
mit
Δϕ
Δt
durchlaufener Drehwinkel in rad
verstrichene Zeit
Dreht sich der starre Körper ungleichförmig um seine Achse, so kann man nur von der
momentanen Winkelgeschwindigkeit sprechen :
ω
=
lim
Δt →0
Δϕ
Δt
=
dϕ
dt
Um endlich auch noch die Richtung zu kennzeichnen, in welcher der
starre
Körper
um
seine
Achse
rotiert,
stellt
man
die
Winkelgeschwindigkeit als Vektor dar und legt sie so in die Drehachse,
wie sich ein mit dem Körper rotierender Korkenzieher verschieben würde.
r
r
Die Winkelgeschwindigkeit ω ist ein Vektor. Die Richtung von ω fällt mit der Drehachse
zusammen und wird durch die Korkenzieherregel festgelegt. Sie hat stets gleiche Richtung
r
wie das Drehmoment M .
r
Der Betrag von ω ist gegeben durch ω
=
Δϕ
Δ t → 0 Δt
lim
=
dϕ
.
dt
r
Die Einheit von ω ist 1 s-1 oder 1 rad/s .
1.6 Winkelbeschleunigung
r
Die momentane Winkelbeschleunigung α ist ein Vektor der gleichen Richtung wie die
r r
momentane Winkelgeschwindigkeit ω . α gibt die Veränderung der Winkelgeschwindigkeit
im Laufe der Zeit an. Es gilt daher :
r
r
r
Δω
dω
=
α = lim
Δ t → 0 Δt
dt
r
Die Einheit der Winkelbeschleunigung α ist 1 s-2 oder 1 rad/s2 .
1.7 Rotationsenergie
Beim Herunterrollen einer Kugel beschreibt der
Schwerpunkt S eine geradlinig beschleunigte Translationsbewegung. Jeder Punkt P außerhalb des Schwerpunkts
beschreibt eine Rotationsbewegung um den Schwerpunkt.
Die Bewegungsenergie oder kinetische Energie EKIN der
Kugel besteht demnach aus 2 Teilen :
•
Translationsenergie ETRA = 1 2 ⋅ m ⋅ v 2
Rotationsenergie
E ROT
•
STARRE KÖRPER 4
Merke :
Dreht sich ein Körper um seine Drehachse, ohne dass die Drehachse ihre
Position ändert (Schleifscheibe, Schwungrad), so entfällt ETRA und EKIN = E ROT .
Zur Berechnung der Rotationsenergie betrachten wir ein Körper der reibungsfrei um eine
feste Achse dreht, so gilt demnach :
=
E ROT
E KIN
Zur Berechnung stellen wir uns den Körper aus unendlich vielen Punktmassen m1 , m2 , m3 ,
... , mn zusammengebaut.
E ROT
E ROT
=
E KIN ,1 + E KIN ,2 + E KIN ,3 + ... + E KIN , n
=
1
=
1
=
1
=
1
=
1
2
m1v12 +
2
m1ω12 r12 +
1
2
m1ω 2 r12 +
1
2
⋅ m1r12 + m2 r22 + m3 r32 + ... + mn rn2 ⋅ ω 2
1
m2 v22 +
2
(
2⋅
n
∑mr
2
i i
1
2
m3v32 + ... +
2
m2ω 22 r22 +
1
2
m2ω 2 r22 +
1
1
2
v =ω⋅r
mn vn2
2
m3ω32 r32 + ... +
1
2
m3ω 2 r32 + ... +
1
)
2
mnω n2 rn2
2
mnω 2 rn2
ω1 = ω2 = ... = ω n = ω
⋅ω2
i =1
Den Ausdruck
n
∑mr
i i
2
bezeichnet der Physiker als Trägheitsmoment
J . Es folgt
i =1
schlußendlich für die Rotationsenergie EROT :
=
EROT
1
2
⋅ J ⋅ ω2
1.8 Trägheitsmoment
Das Trägheitsmoment J ist ein Maß für das Sich Wehren eines starren Körpers gegen die
Änderung seiner reinen Rotationsbewegung.
J
=
n
∑mr
2
i i
i =1
mi
ri
elementare Punktmasse
Entfernung Punktmasse − Drehachse
Die Einheit des Trägheitsmoments ist 1 kg⋅m2 .
Das Trägheitsmoment hängt von der Masse und der Form des Körpers sowie von der Lage
der Drehachse und dem Abstand Drehachse - Schwerpunkt ab.
Die in der Literatur angegebenen Trägheitsmomente J S gelten nur wenn die Drehachse D
durch den Schwerpunkt S des Körpers verläuft.
Liegt die Drehachse außerhalb des Schwerpunktes, so ergibt sich ein größeres
Trägheitsmoment J D , das sich mit dem Satz von Steiner berechnen lässt :
JD
=
J S + m ⋅ a2
mit
a Entfernung Drehachse − Schwerpunkt
STARRE KÖRPER 5
Das Trägheitsmoment macht Körper träger. Ihr Widerstand gegen Änderung des
Bewegungszustandes ist stets größer als der von vergleichbaren reibungsfrei gleitenden
Körpern. Dies lässt sich anschaulich zeigen, wenn Körper gleicher Ausdehnung und gleicher
Masse eine geneigte Ebene reibungsfrei hinabrollen bzw. hinabgleiten lässt : Hohlzylinder,
Vollzylinder, Kugel und Quader.
Bei den Rollkörpern wird die Lageenergie mgh auf die kinetische Energie der Translation des
Schwerpunktes 1 2 mv 2 und die Rotationsenergie
Schwerpunkt aufgeteilt. Also gilt :
1
2
mv 2 +
1
2
Jω 2
=
mgh
=
mgh
=
mgh
1
2
Jω 2 durch die Längsachse um den
ω=
v
r
2
1
v
2 mv + 2 J 2
r
J ⎞
⎛
1 v2 ⎜ m +
⎟
2
r2 ⎠
⎝
2
1
v
=
2mgh
J
m+ 2
r
Man stellt fest, dass die am Fuße der geneigten Ebene erreichte Geschwindigkeit umso
kleiner ist je größer das Trägheitsmoment des Körpers ist. Setzen wir in die Formel die
Ausdrücke der Trägheitsmomente der einzelnen Kérper ein, so erhalten wir :
gleitender Körper :
J =0
⇒
STARRE KÖRPER 6