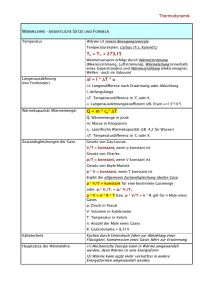
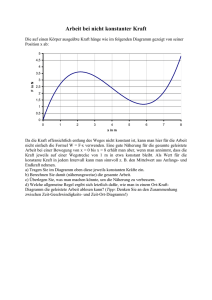
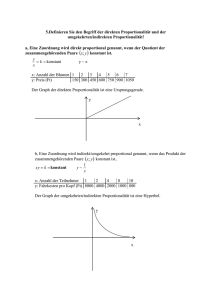
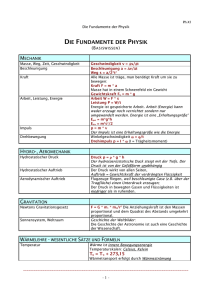
jf(z)j 1 f 2 H( ) - Mathematik, TU Dortmund

1
Prof. Dr. W. Kaballo
Fakultat fur Mathematik
TU Dortmund

4. Ubungsblatt
zur Funktionentheorie I
Wintersemester 2015/16
Aufgabe 13: Berechnen Sie die Wegintegrale
a)
Z
2 (0)
sin z dz ;
z+i
b)
Z
z
1 (1)
(z 1)
n dz ;
c)
Z
dz
3 (2i) z
2
+
2
:
Aufgabe 14: a) Fur eine ganze Funktion f 2 H(C ) sei Re f beschrankt. Zeigen Sie,
dass f konstant ist.
b) Fur f 2 H(C ) gebe es Zahlen ! ; ! 2 C nf0g mit !! 62 R und f (z) = f (z + !) =
f (z + ! ) f
ur alle z 2 C : Zeigen Sie, dass f konstant ist.
c) Fur f 2 H(C ) gelte j f (z) j C (1 + j z j)n fur ein n 2 N und ein C 0 : Zeigen
Sie, dass f ein Polynom von Grad n ist.
0
0
0
0
Aufgabe 15: a) Es seien C oen, K kompakt und " > 0 mit K" :
Zeigen Sie
sup j f (z) j z 2K
1
"2
R
j ( ) j d( ) fur f 2 H(
) :
K" f (1)
b) Folgern Sie, dass die Raume H(
) \ Lp(
) fur 1 p 1 in den Banachraumen
abgeschlossen sind.
Lp (
)
Aufgabe 16: a) Es seien D C ein Gebiet, und fur f 2 H(D) habe j f j ein lokales
Minimum in z 2 G : Zeigen Sie f (z ) = 0 :
0
0
b) Geben Sie mittels a) einen weiteren Beweis des Fundamentalsatzes der Algebra.