Ingenieurmathematik

Mathematik und Naturwissenschaften Fachrichtung Mathematik, Institut für Numerische Mathematik
INGENIEURMATHEMATIK
8. Reihen
Prof. Dr. Gunar Matthies
Sommersemester 2016
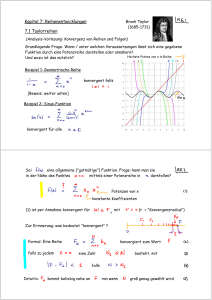
Motivation
Wert einer Summe mit unendlich vielen Summanden bestimmen:
1 1 1
1 + + + + · · · =?
2 4 8
Zunächst Folge der Partialsummen betrachten
1
1 1
1 1 1
1, 1 + , 1 + + , 1 + + + , . . .
2
2 4
2 4 8
Existiert der Grenzwert der Partialsummenfolge, dann setzen wir
ihn als Wert der unendlichen Summe.
1/4
1/16
1/8
1
1/2
G. Matthies
Ingenieurmathematik
2/33
Reihen
Definition
Sei (ak )k∈N0 = (a0 , a1 , a2 , . . . ) eine Folge reeller oder komplexer
Zahlen, d. h. ak ∈ R oder ak ∈ C. Dann heißen die Summen
n
X
sn :=
ak ,
k=0
Partialsummen zur Folge (ak )k∈N0 . Die Folge (sn )n∈N0 wird als
(unendliche) Reihe zur Folge (ak )k∈N0 bezeichnet. Dafür wird kurz
∞
X
ak
geschrieben.
k=0
Bemerkung
Die Folge (ak ) und die Reihe (sn ) beginnen stets beim selben
Index, der aber auch von 0 verschieden sein kann.
G. Matthies
Ingenieurmathematik
3/33
Konvergenz von Reihen
Definition
Eine Reihe
∞
X
ak heißt genau dann konvergent, wenn die Fol-
k=0
ge ihrer Partialsummen (sn ) konvergiert. Gilt s = lim sn , dann
n→∞
bezeichnen wir s als den (Grenz-)Wert der Reihe und schreiben
∞
X
ak = s
k=0
Divergiert die Partialsummenfolge, so heißt die Reihe divergent.
Bemerkung
Der Ausdruck
∞
X
ak hat zwei Bedeutungen:
k=0
1. die Reihe selbst, 2. den Grenzwert der Reihe.
G. Matthies
Ingenieurmathematik
4/33
Geometrische Reihe
Definition
Sei q ∈ C. Dann heißt
∞
X
q k = 1+q +q 2 +q 3 +. . . geometrische
k=0
Reihe.
Es gilt
sn =
n
X
qk =


n + 1,


k=0
Für |q| < 1 gilt
sn →
und somit
−1
, q 6= 1.
q−1
1
−1
=
für n → ∞
q−1
1−q
∞
X
k=0
G. Matthies
q = 1,
q n+1
qk =
1
.
1−q
Ingenieurmathematik
5/33
Harmonische Reihe
Definition
Die Reihe
∞
X
1 1 1
1
= 1 + + + + ...
k
2 3 4
k=1
heißt harmonische Reihe.
Satz
Die harmonische Reihe ist bestimmt divergent.
G. Matthies
Ingenieurmathematik
6/33
Rechnen mit Reihen
Satz
Seien (ak )k∈N0 und (bk )k∈N0 Zahlenfolgen. Wenn die zugehörigen
Reihen konvergieren, dann die Rechenregeln:
∞
∞
∞
X
X
X
(ak + bk ) =
ak +
bk
k=0
k=0
k=0
∞
X
∞
X
∞
X
(ak − bk ) =
k=0
ak −
k=0
bk
k=0
und
∞
∞
X
X
(λak ) = λ
ak
k=0
k=0
für beliebige Zahlen λ.
G. Matthies
Ingenieurmathematik
7/33
Notwendiges Konvergenzkriterium
Satz
Ist die Reihe
∞
X
ak konvergent, dann gilt
k=0
lim ak = 0,
k→∞
d. h., die ursprüngliche Folge (ak )k∈N0 ist eine Nullfolge.
Bemerkung
Die Umkehrung des Satzes gilt nicht. Als Beispiel sei die harmonische Reihe betrachtet.
Der Satz kann zum Beweis der Divergenz von Reihen eingesetzt
∞
X
werden, da lim ak = a 6= 0 die Divergenz der Reihe
ak liefert.
k→∞
G. Matthies
k=0
Ingenieurmathematik
8/33
Einfache Konvergenzaussage
Satz
∞
X
Sei
ak eine Reihe mit reellen, nicht-negativen Gliedern. Dann
k=0
konvergiert die Reihe genau dann, wenn die Folge der Partialsummen nach oben beschränkt ist.
Bemerkung
Selbst wenn die Konvergenz einer Reihe gesichert ist, kann das
Bestimmen des Wertes der Reihe schwierig sein.
G. Matthies
Ingenieurmathematik
9/33
Alternierende Reihen
Definition
Sei (ak )k∈N0 eine Folge reeller Zahlen derart, dass ak ak+1 < 0 für
∞
X
alle k ≥ 0 gilt. Dann heißt
ak alternierende Reihe.
k=0
Bemerkung
Eine alternierende Reihe lässt sich stets als
∞
∞
X
X
k
(−1) bk
oder
(−1)k+1 bk
k=0
k=0
schreiben, wobei (bk )k∈N0 mit bk = |ak | eine Folge mit positiven
Gliedern ist. Das Vorzeichen der Glieder einer alternierenden Reihe
wechselt (alterniert) von Summand zu Summand.
G. Matthies
Ingenieurmathematik
10/33
Leibniz-Kriterium
Satz
∞
X
Sei
ak eine alternierende Reihe. Wenn die Folge |ak |)k∈N0 der
k=0
Beträge eine monotone Nullfolge ist, dann konvergiert die Reihe.
Bemerkung
Die Monotonie der Folge der Beträge ist wesentlich. Die alternierende Reihe

−1


k gerade,
∞
 ,
X
k!
ak
mit ak =

2

k=0

, k ungerade,
k +1
divergiert, da die ungeraden Summanden die harmonische Reihe
bilden.
G. Matthies
Ingenieurmathematik
11/33
Grenzwert einer alternierenden Reihe
Satz
∞
X
Sei
ak eine alternierende Reihe mit Grenzwert s. Dann gilt
k=0
|s − sn | ≤ |an+1 |,
wobei
sn =
n
X
ak
k=0
die n-te Partialsumme der Reihe bezeichnet.
G. Matthies
Ingenieurmathematik
12/33
Absolut konvergente Reihen
Definition
Eine Reihe
∞
X
ak heißt absolut konvergent, wenn die Reihe
k=0
der Absolutbeträge ihrer Glieder konvergiert.
∞
X
|ak |
k=0
Bemerkung
Eine konvergente Reihe mit nicht-negativen reellen Gliedern ak ist
damit immer auch absolut konvergent, da |ak | = ak für alle k gilt.
Satz
Jede absolut konvergente Reihe ist auch konvergent. Die Umkehrung gilt nicht.
G. Matthies
Ingenieurmathematik
13/33
Umordnung von Reihen
Definition
∞
X
Seien
ak eine Reihe und (nk )k∈N0 eine Folge nicht-negativer
k=0
ganzer Zahlen, in der jede Zahl 0, 1, 2, . . . genau einmal vorkommt.
Dann heißt
∞
X
ank
k=0
Umordnung der Ausgangsreihe.
Satz
∞
X
Ist
ak eine absolut konvergente Reihe mit Grenzwert s. Dann
k=0
ist auch jede Umordnung dieser Reihe absolut konvergent und der
Grenzwert der umgeordneten Reihe ist s.
G. Matthies
Ingenieurmathematik
14/33
Multiplikation von Reihen
Seien
gilt
∞
X
ak und
k=0
∞
X
k=0
∞
X
bk zwei absolut konvergente Reihen. Dann
k=0
!
ak
∞
X
!
bk
k=0
=
∞
X
ck
mit ck =
k=0
k
X
ai bk−i
i=0
oder ausgeschrieben
! ∞
!
∞
X
X
ak
bk
k=0
k=0
= a0 b0 + a0 b1 + a1 b0 + a0 b2 + a1 b1 + a2 b0 + . . .
|{z} |
{z
} |
{z
}
= c0
= c1
= c2
Das obige Cauchy-Produkt kann als Verallgemeinerung des Ausmultiplizierens aufgefasst werden.
G. Matthies
Ingenieurmathematik
15/33
Majorantenkriterium
Satz
Gegeben seien die komplexe Reihe
∞
X
∞
X
ak und die reelle Reihe
k=0
bk mit |ak | ≤ bk für alle k ≥ k0 ∈ N. Ist die Reihe
k=0
konvergent, so konvergiert die Reihe
nennt die Reihe
∞
X
∞
X
G. Matthies
bk
k=0
ak sogar absolut. Man
k=0
bk Majorante der Reihe
k=0
∞
X
∞
X
ak .
k=0
Ingenieurmathematik
16/33
Minorantenkriterium
Satz
Seien die reellen Reihen
∞
X
k=0
ak und
∞
X
alle k ≥ k0 ∈ N gegeben. Ist die Reihe
die Reihe
der Reihe
∞
X
bk mit ak ≥ bk ≥ 0 für
k=0
∞
X
bk divergent, dann ist
k=0
ak auch divergent. Die Reihe
k=0
∞
X
∞
X
bk heißt Minorante
k=0
ak .
k=0
G. Matthies
Ingenieurmathematik
17/33
Quotientenkriterium
Satz
Existieren ein q mit 0 < q < 1 und ein k0 ∈ N0 mit
ak+1 ak ≤ q, ak 6= 0 für alle k ≥ k0 ,
dann konvergiert die Reihe
ak absolut.
k=0
Existiert ein k0 ∈ N0 mit
ak+1 ak ≥ 1,
so divergiert die Reihe
∞
X
ak 6= 0 für alle k ≥ k0 ,
∞
X
ak .
k=0
G. Matthies
Ingenieurmathematik
18/33
Bemerkungen
• Im ersten Fall stellt die geometrische Reihe eine konvergente
Majorante dar.
• Im zweiten Fall ist das notwendige Konvergenzkriterium ver-
letzt.
• Der Grenzwert der Reihe kann mit den Quotientenkriterium
nicht bestimmt werden.
ak+1 • Sei W := lim k→∞
ak – Gilt W < 1, dann konvergiert die Reihe absolut.
– Gilt W > 1, dann divergiert die Reihe.
– Gilt W = 1, dann lässt sich so keine Aussage treffen.
G. Matthies
Ingenieurmathematik
19/33
Wurzelkriterium
Satz
Existieren ein q mit 0 < q < 1 und ein k0 ∈ N0 mit
p
k
|ak | ≤ q für alle k ≥ k0 ,
so konvergiert die Reihe
∞
X
ak absolut.
k=0
Gilt für unendlich viele k ∈ N
p
k
dann divergiert die Reihe
∞
X
|ak | ≥ 1,
ak .
k=0
G. Matthies
Ingenieurmathematik
20/33
Bemerkungen
• Im ersten Fall stellt die geometrische Reihe eine konvergente
Majorante dar.
• Im zweiten Fall ist das notwendige Konvergenzkriterium ver-
letzt.
• Der Grenzwert der Reihe kann mit den Wurzelkriterium nicht
bestimmt werden.
p
• Sei Q := lim k |ak |
k→∞
– Gilt Q < 1, dann konvergiert die Reihe absolut.
– Gilt Q > 1, dann divergiert die Reihe.
– Gilt Q = 1, dann lässt sich so keine Aussage treffen.
G. Matthies
Ingenieurmathematik
21/33
Potenzreihe
Definition
Seien (ak )k∈N0 eine Zahlenfolge und x0 ∈ C. Dann heißt
∞
X
ak (x − x0 )k ,
x ∈ C,
k=0
Potenzreihe in x zum Entwicklungspunkt x0 . Die Zahlen ak werden
Koeffizienten der Potenzreihe genannt.
Bemerkung
Eine Potenzreihe ist, im Unterschied zu den bisher betrachteten
Reihen, die Summation einer Folge von Funktionen. Wird die Potenzreihe für ein festes x betrachtet, dann entsteht eine Reihe im
bisherigen Sinn.
n
P
ak (x − x0 )k sind Polynome.
Die Partialsummen Sn (x) =
k=0
G. Matthies
Ingenieurmathematik
22/33
Taylor-Polynome
Erinnerung
Definition
Seien f : (a, b) → R eine (n + 1)-mal differenzierbare Funktion
und x0 ∈ (a, b). Dann bezeichnen wir
Tn (x) := f (x0 ) + f 0 (x0 )(x − x0 ) +
f 00 (x0 )
(x − x0 )2 + . . .
2!
f (n) (x0 )
(x − x0 )n
n!
als das n-te Taylor-Polynom von f an der Stelle x0 . Das Restglied
Rn (x) := f (x) − Tn (x) hat die Darstellung
+
Rn (x) =
f (n+1) (ξ)
(x − x0 )n+1 ,
(n + 1)!
wobei ξ zwischen x0 und x liegt, was ξ = x0 + ϑ(x − x0 ) mit
ϑ ∈ (0, 1) bedeutet.
G. Matthies
Ingenieurmathematik
23/33
Taylor-Reihe
Definition
Seien (a, b) ⊂ R ein Intervall, f : (a, b) → R eine beliebig oft
differenzierbare Funktion und x0 ∈ (a, b). Dann heißt
T (x) :=
∞
X
f (k) (x0 )
k=0
k!
(x − x0 )k
die Taylor-Reihe von f zum Entwicklungspunkt x0 .
Bemerkung
Die Taylor-Reihe muss nicht für alle x ∈ (a, b) konvergieren. Selbst
wenn sie für ein x ∈ (a, b) konvergiert, dann muss der Wert der
Reihe nicht notwendigerweise mit f (x) identisch sein.
G. Matthies
Ingenieurmathematik
24/33
Konvergenz von Taylor-Reihen
Satz
Seien (a, b) ⊂ R ein Intervall und f : (a, b) → R eine beliebig oft
differenzierbare Funktion. Die Taylor-Reihe von f zum Entwicklungspunkt x0 ∈ (a, b) konvergiert an der Stelle x ∈ (a, b) genau
dann gegen f (x), wenn das Restglied Rn (x) für n → ∞ gegen 0
konvergiert.
Beispiel
( 1 2
e − /x , x 6= 0,
f : R → R, f (x) =
0,
x = 0,
f ist in x0 = 0 beliebig oft differenzierbar mit f (k) (0) = 0, k ∈ N0
∞
X
f (k) (0)
Taylor-Reihe T (x) =
(x − 0)k = 0 stimmt nur für
k!
k=0
x = 0 mit Funktionswert von f überein
G. Matthies
Ingenieurmathematik
25/33
Konvergenzbereich
Definition
∞
X
Sei
ck (z −a)k eine Potenzreihe zum Entwicklungspunkt a ∈ C
k=0
mit komplexen Koeffizienten. Dann heißt die Menge
(
)
∞
X
z ∈C :
ck (z − a)k konvergiert
k=0
Konvergenzbereich der Potenzreihe.
Bemerkung
Der Konvergenzbereich ist stets nicht-leer, da die Potenzreihe zum
Entwicklungspunkt a für z = a auf jeden Fall konvergiert.
Es gibt Potenzreihen, deren Konvergenzbereich alle komplexen
Zahlen umfasst.
G. Matthies
Ingenieurmathematik
26/33
Konvergenzradius
Definition
∞
X
Sei
ck (z −a)k eine Potenzreihe zum Entwicklungspunkt a ∈ C
k=0
mit komplexen Koeffizienten. Der Konvergenzradius r der Potenzreihe ist eine nicht-negative reelle Zahl oder ∞ derart, dass die
Potenzreihe für alle z ∈ C mit |z − a| < r konvergiert und für alle
z ∈ C mit |z − a| > r divergiert.
Bemerkung
Das Konvergenzverhalten für z ∈ C mit |z −a| = r muss gesondert
untersucht werden.
Der Konvergenzradius ist auch gegeben durch
∞
X
k
r = sup |z − a| :
ck (z − a) konvergiert .
k=0
G. Matthies
Ingenieurmathematik
27/33
Eindeutigkeit der Potenzreihenentwicklung I
Satz
Seien a ∈ C, B = {x ∈ C : |x − a| < r } mit r > 0, B ⊂ D und
f : D → C. Gilt
∞
X
f (x) =
ak (x − a)k
k=0
für alle x ∈ B, dann ist
f (k) (a)
k!
für alle k ≥ 0. Die Reihe ist also genau die Taylor-Reihe von f
zum Entwicklungspunkt a.
ak =
G. Matthies
Ingenieurmathematik
28/33
Eindeutigkeit der Potenzreihenentwicklung II
Folgerung
Seien a ∈ C und B = {x ∈ C : |x − a| < r } mit r > 0. Weiterhin
seien
∞
∞
X
X
k
f (x) =
ak (x − a)
und
g (x) =
bk (x − a)k
k=0
k=0
zwei Potenzreihen, die in B konvergieren.
Gibt es eine Folge (xk )k∈N0 mit lim xk = a und xk 6= a für alle
k→∞
k ∈ N0 derart, dass zusätzlich f (xk ) = g (xk ) erfüllt ist, dann gilt
f (x) = g (x) für alle x ∈ B und ak = bk für alle k ≥ 0.
G. Matthies
Ingenieurmathematik
29/33
Satz von Cauchy–Hadamard
Satz
∞
X
Sei
ck (z − a)k eine Potenzreihe mit Entwicklungspunkt a ∈ C.
k=0
• Falls
ck ∈ [0, ∞]
r := lim k→∞ ck+1 existiert, dann hat die Potenzreihe den Konvergenzradius r .
• Falls
1
r := lim p
∈ [0, ∞]
k
k→∞
|ck |
existiert, dann hat die Potenzreihe den Konvergenzradius r .
G. Matthies
Ingenieurmathematik
30/33
Rechnen mit Potenzreihen I
Satz
Seien
∞
X
∞
X
ak (z − a)k und
k=0
bk (z − a)k zwei Potenzreihen zum
k=0
Entwicklungspunkt a ∈ C, die in B = {z ∈ C : |z − a| < r } mit
r > 0 konvergieren. Dann gelten die Rechenregeln
∞
∞
∞
X
X
X
•
ak (z − a)k ±
bk (z − a)k =
(ak ± bk )(z − a)k
•
k=0
∞
X
k=0
!
ak (z − a)k
k=0
∞
X
k=0
!
bk (z − a)k
k=0
=
∞
k
X
X
k=0
!
ak−i bi
(z − a)k
i=0
für alle z ∈ B.
G. Matthies
Ingenieurmathematik
31/33
Rechnen mit Potenzreihen II
Satz
∞
X
Sei
ak (x−a)k eine reelle Potenzreihe um a ∈ R, die im Intervall
k=0
(a − r , a + r ) mit r > 0 konvergiert. Dann haben wir
∞
∞
X
d
d X
ak (x − a)k =
ak (x − a)k
dx
dx
k=0
k=0
∞
X
=
ak k(x − a)k−1
k=1
Z X
∞
ak (x − a)k dx =
k=0
∞ Z
X
ak (x − a)k dx
k=0
∞
X
ak
(x − a)k+1 + C
=
k +1
k=0
für alle x ∈ (−r , r ).
G. Matthies
Ingenieurmathematik
32/33
Beispiele für Potenzreihen
∞
ex = 1 + x +
X xk
x2
+ ... =
,
2!
k!
x ∈ C,
k=0
1
= 1 + x + x2 + . . .
1−x
sin x = x −
cos x = 1 −
ln(1 + x) = x −
=
x3 x5
+
− ... =
3!
5!
x2
2!
+
x4
4!
− ... =
x2 x3
+
− ... =
2
3
=
∞
X
k=0
∞
X
xk,
(−1)k
x 2k+1
, x ∈ C,
(2k + 1)!
(−1)k
x 2k
,
(2k)!
(−1)k
x k+1
,
k +1
k=0
∞
X
k=0
∞
X
k=0
∞
X
(−1)k+1
k=1
G. Matthies
|x| < 1,
Ingenieurmathematik
xk
,
k
x ∈ C,
x ∈ (−1, 1],
33/33