Übungsblatt 1

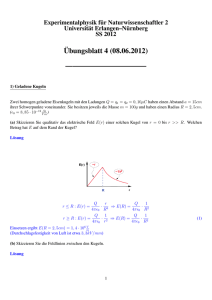
Übungsblatt 1 - LÖSUNGEN
zur Vorlesung EP1 (Prof. Grüner) im SoSe 2011
13. Mai 2011
1.1
Bohrsches Atommodell
Gemäÿ dem Bohrschen Atommodell des Wasserstoatoms umkreist ein negativ geladenes Elektron den Atomkern, der aus einem einzigen positiv geladenen Proton besteht.
Elektron und Proton tragen die Elementarladung e = 1.6·10−19 C, jeweils
mit umgedrehtem Vorzeichen. Das Elektron umkreist den Kern im Abstand
r = 0.53 · 10−10 m.
1. Wie groÿ ist die durch den Kern bedingte elektrische Feldstärke am
Ort des Elektrons?
Lösung:
E=
e
1
· 2 = 5.1 · 1011 V /m
4π0 r
mit 0 = 8.85 · 10−12 As/V m
2. Wie groÿ ist die elektrische Kraft Fel zwischen Elektron und Proton?
Lösung:
F = qE = 8.2 · 10−8 N
3. Wie groÿ ist die Geschwindigkeit des Elektrons (me = 9.11 · 10−31 kg)?
Lösung: Die Zentrifugalkraft muss gleich der Zentripetalkraft sein, die
in diesem Fall der in b) berechneten elektrischen Kraft entspricht.
mv 2
= 8.2 · 10−8 N ⇒ v =
r
s
8.2 · 10−8 N 0.53 · 10−10 m
= 2.2 · 106 m/s
9.11 · 10−31 kg
4. Wie groÿ ist die sog. Ionisierungsarbeit, d.h. die Arbeit, die notwendig ist, um das Elektron aus dem Anziehungsbereich des Protons (ins
Unendliche) zu entfernen?
Lösung: Das Teilchen bendet sich im elektrischen Potential. Dieses ist
per Konvention so deniert, dass sein Wert im Unendlichen Null ist.
Bewegt man eine negative Ladung auf eine positive zu, verringert sich
1
die potentielle Energie, da sich beide Teilchen anziehen, die potentielle
Energie wird also negativ. Dass ein Teilchen ins Unendliche entwischen
kann, muss seine Gesamtenergie also mindestens gleich Null sein:
EGes = EKin − EP ot
Berechnung von EP ot :
Z
EP ot
r
~ =− 1
=−
F~C dr
4π0
∞
Z
r
∞
−e2
e2
=
r2
4π0
Z
r
∞
1
e2
=
−
r2
4π0 r
Berechnung von EGes :
EGes
me v 2
e2
−
= −2.18 · 10−18 J = 13.6eV
=
2
4π0 r
Es müssen also 13.6 eV zugeführt werden, um ein Wassertoatom zu
ionisieren.
5. Welche Geschwindigkeit müsste das Elektron also haben, um sich beliebig weit vom Proton entfernen zu können?
Lösung:
EKin + EP ot = 0 ⇒ EKin = −EP ot
s
me v 2
e2
e2
=
⇒v=
= 3.1 · 106 m/s
2
4π0 r
2πme 0 r
1.2
Kugeln am Faden
Zwei mit isolierten Fäden von 100 mm Länge am gleichen Punkt aufgehängte
Kugeln mit einer Masse von 0.5 g werden elektrisch aufgeladen (beide Kugeln
mit gleicher Ladung q ). Danach bilden die Fäden der sich abstoÿenden Kugeln
einen Winkel von α = 75◦ miteinander. Wie groÿ sind die Ladungen der
Kugeln?
Lösung: Die elektrische Kraft drückt die beiden Kugeln auseinander, während die Schwerkraft beide zusammendrückt. Es stellt sich dann ein Gleichgewicht ein, wenn kein Drehmoment auf die Ladungen am Faden wirkt. Dies
ist dann der Fall, wenn Fe0 = FG0 ist. Der markierte Winkel bei Fe ist der
gleiche, den der Faden mit der Waagrechten einschlieÿt, und lässt sich über
die Winkelsumme im Dreieck zu 52.5◦ bestimmen. Da das durch die Gravitationsvektoren aufgespannte Dreieck dem der elektrischen Kräfte entspricht,
nur um 90◦ gedreht, ist auch der zweite markierte Winkel 52.5◦ . Daraus folgt:
2
Fe0 = Fe sin(52.5◦ )
FG0 = FG cos(52.5◦ )
wobei FG = mg und Fe = 4π1 0 qr2 sind. d ist der Abstand der beiden
Ladungen, also d = 2 · 100mm · sin(37.5◦ ), Gleichsetzen von Fe0 und FG0
ergibt:
2
mg cos(52.5◦ ) =
Auösen nach q ergibt
1.3
1
q2
· sin(52.5◦ )
4π0 (2 · 100mm · sin(37.5◦ ))2
q = 7.9 · 10−8 C
E-Feld zweier Punktladungen
Zwei Punktladungen q1 und q2 = 3q1 sind 60 cm voneinander entfernt. An
welcher Stelle auf einer Geraden, welche die Punkte miteinander verbindet
ist das elektrische Feld Null?
Lösung: Die E-Felder der Punktladungen sind
E1 =
1
q1
· 2
4π0 r1
E2 =
1
q2
· 2
4π0 r2
Auf der Achse wirken die Felder in entgegengesetzter Richtung. Gleichsetzen der beiden Felder ergibt:
q1
q2
= 2
2
r1
r2
Einsetzen von r2 = 60cm − r1 und q2 = 3q1 führt zu:
(60cm − r1 )2 = 3r12 .
3
Zieht man die Wurzel und formt um, erhält man:
60cm = r1 ±
√
3r1 = (1 ±
√
3)r1 .
Als Lösungen ergeben sich:
r1 = 22cm und r1 = −82cm
Da negative Radien keinen physikalischen Sinn ergeben, ist das einzig
richtige Ergebnis 22 cm.
4