14. Strömende Flüssigkeiten und Gase

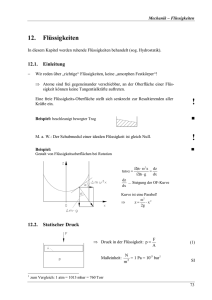
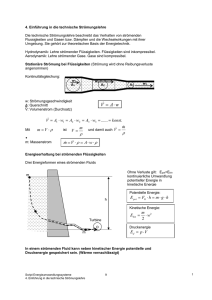
Mechanik – Strömende Flüssigkeiten und Gase
14.
Strömende Flüssigkeiten und Gase
14.1. Vorbemerkungen
−
Es gibt viele Analogien zwischen Flüssigkeiten und Gasen (wegen der freien
Verschiebbarkeit der Teilchen); Hauptunterschied liegt in der Kompressibilität
jedoch:
Bei v << vSchall verhalten sich auch strömende Gase praktisch inkompressibel,
d.h. es erfolgt kein Aufbau von Druckwellen.
!
⇒ Daher im folgenden Annahme eines inkompressiblen Fluids.
−
Beschreibung von Strömungen nach EULER (1707 - 1783) anhand des Ger
schwindigkeitsfeldes v( r ) .
r
Sonderfall: v( r ) = zeitlich const. ⇒ stationäre Strömung
−
stationäres Strömungsfeld beschrieben durch Stromlinien:
Stromröhre = Bündel von Stromlinien
Tangente an der Stromlinie
r
→ Richtung von v
Dichte der Stromlinien
r
→ Betrag von v
−
Die Abbildung zeigt, dass pro Zeiteinheit ∆t ein strömendes Volumenelement
∆V an jeder Stelle der Stromröhre konstant ist
∆V
V& =
= A ⋅ v = const . (innerhalb der Stromröhre)
∆t
& ... Volumenstrom
V
(1)
Gl. (1) heißt Kontinuitätsgleichung: Wenn in der Stromröhre kein Medium erzeugt oder vernichtet wird, muss I konstant bleiben und v sich entsprechend A
einstellen.
!
Kommentar:
Hier ist die Quellen- und Senkenfreiheit eigentlich fast selbstverständlich (ein
Beispiel für eine Ausnahme wäre eine chemische Reaktion im strömenden Gas,
die das Volumen verändert). In der Elektrodynamik ist das anders, obwohl ansonsten viele Analogien existieren!
u
85
Mechanik – Strömende Flüssigkeiten und Gase
14.2. Innere Reibung
... in strömenden Medien
n
Beispiel: Löffel aus Honig herausziehen
⇒ Geschwindigkeitsübergang...
von v = 0 (entfernt vom Löffel)
auf v = vLöffel (an der Löffel-Oberfläche)
−
Es zeigt sich, dass für die Reibungskraft FR gilt
dv
dx
A ... Wechselwirkungsfläche
FR ~ A ⋅
mit:
dv 1
dx
η ... Viskosität, dynamische Zähigkeit
FR = η ⋅ A ⋅
mit:
FR
dv
= η⋅
A
dx
τR ... Re ibungs-Schubspannung; viskose Schubspannung
τR =
N ⋅s
Maßein[η] =
heit:
m2
(2)
(3)
SI
Gl. (2), (3) heißen NEWTONsches Gesetz der inneren Reibung.
Beispiele:
Substanz
Glycerin
H2 O
Luft
H2
1
20°C
0°C
20°C
100°C
0°C
0°C
η in Nsm-2
1,53
0,0018
0,0010
0,0003
0,00002
0,00001
Vorzeichen in Gl. (2) stimmt, da
n



(typisch: Abnahme mit steigendem T!)
dv
< 0!
dx
86
Mechanik – Strömende Flüssigkeiten und Gase
−
Deutung:
Überwindung der Potentialhügel beim
Gegeneinander-Verschieben der Flüssigkeitsschichten
−
Strömungen, deren Verhalten durch die innere Reibung bestimmt ist, d.h., bei
denen sich nicht vermischende Schichten des Mediums gegeneinander verschoben werden, heißen laminare Strömungen.
!
14.3. Beispiele für laminare Strömungen
14.3.1. Laminare Rohströmung
−
Die Flüssigkeit haftet an der Wand und
hat in der Mitte des Rohres maximale Geschwindigkeit
−
Wir betrachten nun einen Flüssigkeitszylinder um die Rohrachse:
−
An der Mantelfläche wirkt die Reibungskraft (mit Gl. (2))
FR = 2 πrl ⋅ η ⋅
dv
dr
(4)
â
(= AMantel)
−
Auf seine Grund- und Deckflächen wirkt die Netto-Druckkraft
Fp = πr 2 ( p1 − p 2 )
â
(= AGrund/Deck)
(5)
Fp treibt die Flüssigkeit voran und überwindet genau FR : Fp = FR.
87
Mechanik – Strömende Flüssigkeiten und Gase
⇒ aus (4), (5) erhalten wir
dv p1 − p 2
=
⋅r
dr
2ηl
und nach Integration
v( r ) =
(
∆p 2 2
R −r
4ηl
)
(6)
Dies ist ein parabolisches Geschwindigkeitsprofil v(r) = A - B ž r2 , wie in der
Skizze schon gezeigt.
−
&
Interessant ist die Durchflussmenge V
(Volumen/Zeit) bei gegebenen ∆p, η, R.
Wir betrachten einen Hohlzylinder mit
der Dicke dr:
Der Volumenstrom im Querschnitts-Flächenelement dA ist
(dz ž dA = dV!)
á
dV
dz
= ⋅ dA = v( r ) ⋅ 2 πr dr
dt Fl.− Element dt
Gesamt-Volumenstrom im Rohr durch Integration über alle Flächen-Elemente:
R
V& = ∫ v( r ) ⋅ 2πr dr
0
mit v(r) lt. Gl. (6) folgt
π
V& =
⋅ ∆p ⋅ R 4
8ηl
(7)
Dies ist das HAGEN-POISEUILLEsche Gesetz.
u
Kommentar:
Radius geht mit 4. Potenz ein!


Gl. (7) stellt das „OHM sche

Gesetz für die laminare Ro h- 

strömung“ dar:

I =
& =
V
U
R
Triebkraft
∆p
=
(Strömungs −)Widerstan d  8ηl 
 4
 πR 
88
Mechanik – Strömende Flüssigkeiten und Gase
14.3.2. Laminares Umströmen einer Kugel
−
An diesem Beispiel soll eine in der Strömungsmechanik häufig verwendete, sehr
nützliche Betrachtungsweise erläutert werden: die Unterteilung in einen Nahbereich,
in dem das Fluid anhaftet, und den unbeeinflussten Außenbereich der Strömung.
−
Experiment: Wir ziehen eine Kugel mit der Geschwindigkeit v durch eine Flüssigkeit.
·
Nahe Kugel-Oberfläche ist Strömungsgeschwindigkeit = v
(Anhaften der Flüssigkeit)
·
In einiger Entfernung von der Kugel
ruht die Flüssigkeit („merkt nichts“) 1
dv v
≈ ; Wechselwirkungs-Fläche A = Kugel-OF = 4πr2
dr r
⇒
Damit ergibt sich für Gl. (2)
dv
v
= η ⋅ 4π r 2 ⋅
dx
r
FR = −4πrηv
FR = η ⋅ A ⋅
Die ungleich schwierigere korrekte Herleitung lieferte
FR = −6πrηv
(3 - 19)
14.4. Turbulente Strömungen, Ähnlichkeit, Strömungsgrenzschicht
−
Experiment zeigt: Bei bestimmter Geschwindigkeit bricht laminare Strömung
zusammen: Wirbelbildung; Nichtlinearität, chaotisches Verhalten = Turbulenz
−
Es zeigt sich, dass vkrit in Abhängigkeit von
·
ρ
... Dichte
·
η
... Viskosität
·
l
... Abmessung (z.B. Kugel-Durchmesser)
!
unterschiedliche Werte annehmen kann
−
also: entscheidend ist nicht v, sondern eine Größe Re
ρ⋅ v⋅l
η
Re ... REYNOLDsche Zahl
Re ≡
1
!
(8)
Die hier betrachete "r-Umgebung" ist nicht identisch mit der Grenzschichtdicke in <14.4>.
89
Mechanik – Strömende Flüssigkeiten und Gase
l ist eine typische Abmessung des strömenden Systems.
Re ist dimensionslos:
Maßeinheit:
[Re] =
kg m m m ⋅ s
⋅ ⋅ ⋅
=1
m 3 s 1 kg
SI
Re hat die physikalische Bedeutung des Quotienten aus kinetischer Energie und
Reibungsenergie.
−
Bei einem bestimmten Re schlägt die Strömung um. Der Übergang ist jedoch
nicht scharf, sondern ein Bereich (z.B. Re = 1000 - 2000)1
!
Gründe:
·
Einfluss der Oberflächen-Rauheit, u.ä.
·
Strömung kann „instabil-laminar“ sein (gewisse Analogie zur unterkühlten
Flüssigkeit)
−
Strömungen mit gleicher Re sind ähnlich → Modellierung im Wind- oder
Strömungskanal
!
kleines l (Schiffsmodell) ⇒ Anpassung von v sowie gegebenenfalls ρ, η damit
gleiches Re herauskommt.
−
Strömungsgrenzschicht: Fluid haftet an umströmten Oberflächen (Kugel,
Rohrwandung), d.h. v = 0, und gleicht sich dann allmählich an die in einiger
Entfernung herrschende „ungestörte Strömung“ an.
Beispiel:
⋅
Fluid an einer Wand
⋅
Herausziehen einer Platte aus
ruhendem Fluid
n
Die beiden dargestellten Fälle sind völlig analog!
1
Deswegen ist die Frage „Was ist die typische Länge bei einer bestimmten unregelmäßigen
Form?“ auch nicht so kritisch!
90
Mechanik – Strömende Flüssigkeiten und Gase
−
Übergangsbereich wird durch Grenzschicht definierter Dicke D mit linearem
Geschwindigkeitsübergang angenähert (s. Abbildung zur bewegten Platte):
x

v( x) = v 0 ⋅ 1 − 
 D
=0
für x < D
für x ≥ D





(9)
Mit Gl. (9) vereinfacht sich das NEWTONsche Reibungsgesetz (Gl. (2)) zu
v0
D
â
dv
(= )
dx
FR = − η ⋅ A ⋅
(10)
Um die Platte herauszuziehen, muss stetig eine Kraft F = - FR aufgewandt werden. Diese führt lt. Gl. (3 - 6) zu einem Impulsübertrag an das Fluid:
F=
dp
dt
(3 - 6)
⇒ Wenn F = - FR die Zeit ∆t lang wirkt, wird übertragen:
( v 0 ⋅ ∆t = l ... herausgezogene Länge)
á
v0
∆p = F ⋅ ∆t = −FR ⋅ ∆t = +η ⋅ A ⋅ ⋅ ∆t
D
(11)
∆p findet sich im Fluid wieder, das - in seinen einzelnen Schichten
unterschiedlich – beschleunigt wurde: Aufintegration des im Fluid
steckenden Impulses:
D
∆p = ∫ v ( x) ⋅ dm
dm = ρ ⋅ dV = ρ ⋅ A ⋅ dx
0
D
∆p = ρ ⋅ A ⋅ ∫ v( x ) dx
0
x

v( x ) = v 0 ⋅ 1 − 
D

lt. Gl. (9)
D
x

∆p = ρ ⋅ A ⋅ v 0 ⋅ ∫  1 −  dx
D
0
D
∆p = ρ ⋅ A ⋅ v 0 ⋅
2
(12)
91
Mechanik – Strömende Flüssigkeiten und Gase
Wegen der Impulserhaltung müssen (11) und (12) gleich sein
⇒
mit
l
D
= ρ ⋅ A ⋅ v0 ⋅
D
2
2ηl
D=
ρv 0
η⋅A⋅
(13)
D ist die Dicke der (P RANDTLschen) Strömungsgrenzschicht.
u
Kommentar:
·
·
·
Gl. (13) ist eine Näherung, gibt die Tendenz der Abhängigkeit von η, l, ρ, v0 .
l hat die Bedeutung einer charakteristischen Länge.
Die Annahme, dass v(x) linear ist, gilt natürlich besonders für D << l, wenn
„das Fluid nur eine große ebene Wand sieht“:
D=
2ηl
<< l
ρv 0
2η l
<< l 2
ρv 0
ρv 0 l
2 <<
= Re
η
|[
]2
|⋅
ρv 0
η
≡ (8)
Also: Die Näherung des linearen v(x)-Verlaufs gilt für große Re, wo unter Umständen bereits Turbulenz auftritt.
−
Bedeutung der Strömungsgrenzschicht
a)
als Modell:
b) physikalisch: Durch das „Anhaften“ der Strömung wird der Transport beeinflusst: Feuchtigkeit, Wärme usw. müssen durch D hindurch diffundieren; die Möglichkeiten des zwangsweisen Anoder Abtransports enden am Grenzschichtrand.
Jedoch: großes v0 ⇒ kleines D ⇒ Transport erleichtert!
14.5. Reibungsfreies Fluid: BERNOULLIsche Gleichung
−
Wir betrachten jetzt ein reibungsfreies Fluid, d. h. eine existierende Druckdifferenz (p1 ≠ p2 ) wird nicht zur Aufrechterhaltung der Strömung benötigt.
92
Mechanik – Strömende Flüssigkeiten und Gase
−
Das Rohr weise eine Verengung auf:
Wegen der Gültigkeit der Kontinuitätsgleichung (Gl. (1)) ist
∆V
V& =
= A 1 ⋅ v1 = A 2 ⋅ v 2 = const .
∆t
(1‘)
⇒ Im Beispiel lt. Abbildung nimmt v zu!
Ebenfalls verändert sich an der Verengung der Druck von p1 auf p2 :
Druckarbeit links:
∆W1 = p1A1 ⋅ ∆x1 = p1 ⋅ ∆V
â
(= F1 )
Druckarbeit rechts:
∆W2 = p 2 A 2 ⋅ ∆x 2 = p 2 ⋅ ∆V
â
(= F2 )
∆W1 wird zum Teil verwendet, den Druck p2 zu überwinden, also W2 zu leisten.
Der Rest (= ∆W1 - ∆W2 ) wird zur Beschleunigung des Fluids aufgewendet:
∆W1 − ∆W2 = (p1 − p 2 ) ⋅ ∆V =
1
⋅ ρ ⋅ ∆V ⋅ ( v 22 − v12 )
2
â
(= ∆m)
(14)
nach Umstellung folgt
p1 +
ρ 2
ρ
v1 = p1 + v 22
2
2
verallgemeinert
p+
ρ 2
v = p ges = const .
2
(15)
Dies ist die BERNOULLIsche Gleichung.
93
Mechanik – Strömende Flüssigkeiten und Gase
ρ 2
v hat die Dimension eines Druckes1 und heißt Staudruck. p heißt statischer Druck.
2
u
Kommentar:
·
·
−
Für v = 0 ist p = pges, der (maximale) statische Druck. Mit zunehmendem v
sinkt p.
Bei p = 0 („druckloser Ausfluss“) wird der Staudruck maximal. Wird v reduziert, baut sich wieder zunehmender p auf.
Bisher betrachtet: Waagerechte Strömung, d.h. potentielle Energie im Erdschwerefeld war konstant. Wenn wir unterschiedliche Höhen
einbeziehen wollen, müssen wir noch den Schweredruck 2
ρžgžh berücksichtigen und erhalten:
p+
ρ 2
v + ρ ⋅ g ⋅ h = p ges = const .
2
(16)
Dies ist die verallgemeinerte BERNOULLIsche Gleichung.
−
Die BERNOULLI sche Gleichung ist der Energiesatz (bezogen auf das Volumen)
für das Fluid. Diesbezügliche Bedeutung der einzelnen Glieder:
E pot
m
⋅g ⋅h =
V
V
m
E
ρ 2
v = V v 2 = kin
2
2
V
A⋅x
Druckarbei t
p=
⋅p
=
V
V
ρgh =
−
(Staudruck)
(statischer Druck)





·
hydrodynamisches Paradoxon
Bunsenbrenner
Wasserstrahlpumpe
Zerstäuber
·
Kavitation: Wir betrachten Gl. (15) und formen um
·
·
⇒
2
(Schweredruck)
Beispiele zur BERNOULLI schen Gleichung
·
1
!
v=
2 p ges
v>
2 p ges
ρ
ρ
"v ↑ ⇒ p ↓"
entspricht p = 0
entspricht einem statischen Druck p < 0!
kg m 2
m 1
N
Kraft
⋅ 2 = kg ⋅ 2 ⋅ 2 = 2 →
!
2
m s
s m
m
Fläche
kg m
m 1
N
Kraft
Dimension von ρ ⋅ g ⋅ h : 3 ⋅ 2 = kg ⋅ 2 ⋅ 2 = 2 →
!
m s
s m
m
Fläche
94
Mechanik – Strömende Flüssigkeiten und Gase
Dies unter Umständen leicht erreicht, z.B. bei H2 O für v ≥ 14m ž s-1
⇒ Bildung von Dampf-/Gasbläschen (z.B. verdampfte Flüssigkeit)
die bei Reduzierung von v implosionsartig zusammenbrechen
⇒ Druckwellen → Materialzerstörung (Kavitation)
·
Dynamischer Auftrieb:
Infolge der Anfahrtswirbel entsteht Tragflächenumströmung:
vo > vu ⇒ po < p u ⇒ Auftrieb
14.6. Strömungswiderstand
−
... kann über die BERNOULLI sche Gleichung verstanden werden:
a)
langsame Strömung ⇒ völlig symmetrisches Bild
v-Verteilung vor und hinter der Kugel
gleich ⇒ keine resultierende Kraft
b) schnelle Strömung ⇒ Bildung von Wirbeln hinter dem Hindernis:
v hinter der Kugel erhöht (Die „unregelmäßige Richtung“ von v spielt keine
Rolle, die BERNOULLI sche Gleichung ist
eine Energieangelegenheit!)
⇒ statischer Druck p hinter der Kugel
ist reduziert
⇒ Kraft, die die Kugel mitreißen will
−
Diese „Druckwiderstandskraft“ ist dem Staudruck proportional.
(= Staudruck)
á
1 2
F = c w ⋅ ρv ⋅ A
2
A ... Querschnittsfläche
cw... Widerstandsbeiwert
Kommentar:
·
(17)
u
Wir sind wieder ein mal am Rand der Gültigkeit des Modells. Die Initiierung des Wirbelfeldes setzt natürlich Reibung voraus, wenn auch dann die
Argumentation wieder auf der BERNOULLI schen Gleichung beruht.
95
Mechanik – Strömende Flüssigkeiten und Gase
·
−
Deutung: Staudruckabhängigkeit (Staudruck korreliert mit Ekin , s.o.) deshalb, weil infolge Wirbelbildung diese Ekin der Kugel „nur von vorn, nicht
auch von hinten“ zugeführt wird ⇒ resultierende Kraft!
cw ist abhängig von der Körperform. Beispiele (Strömung von links):
1,35
!
1,12
0,40
0,056
(PKW
0,25 ... 0,50)
96