htbla vöcklabruck stet - lernplattform.schule.at

HTBLA VÖCKLABRUCK
STET
Zahlenbereiche
2
INHALTSVERZEICHNIS
1. DIE MENGE DER NATÜRLICHEN ZAHLEN ( /N)............................................... 3
2. DIE MENGE DER GANZEN ZAHLEN (Z)............................................................ 3
3. DIE MENGE DER RATIONALEN ZAHLEN(Q) .................................................... 4
4. DIE MENGE DER REELLEN ZAHLEN (/R) ......................................................... 5
5. DIE MENGE DER KOMPLEXEN ZAHLEN (C) .................................................... 5
6. ÜBERSICHT ÜBER DIE ZAHLENBEREICHE..................................................... 5
© HTBLA Vöcklabruck - STET
Zahlenbereiche
3
1. DIE MENGE DER NATÜRLICHEN ZAHLEN ( /N)
/N = {0,1,2,3,4,5,.......}
/N ist eine unendliche Menge.
Echte Teilmengen von /N:
/Ng = {2,4,6,8,...}
/Nu = {1,3,5,7,...}
Es gilt: Sind a und b zwei natürliche Zahlen, so ist ihre Summe bzw. ihr Produkt
ebenfalls eine natürliche Zahl.
d.h. a ∈/N, b ∈ /N ==> a + b ∈ /N
==> a . b ∈ /N
Bsp.: 3 + 4 = 7
3.4 = 12
Man sagt: Die Menge der natürlichen Zahlen ist abgeschlossen gegenüber der Addition und
der Multiplikation.
ABER: Die Subtraktion und Division sind in /N nicht unbeschränkt durchführbar !
Bsp.:
3 - 4 = -1 ∉ /N
3 : 4 = 0,75 ∉ /N
2. DIE MENGE DER GANZEN ZAHLEN (Z)
Z = {.....,-3,-2,-1,0,1,2,3,.....}
Echte Teilmengen:
Z+ = {1,2,3,...}
Z- = {...,-3,-2,-1}
Z ist eine unendliche Menge.
Es gilt: Die Menge der ganzen Zahlen ist abgeschlossen gegenüber der Addition,
Subtraktion und Multiplikation.
© HTBLA Vöcklabruck - STET
Zahlenbereiche
4
d.h. a,b ∈ Z
==>
a+b ∈Z
a-b ∈Z
a.b ∈Z
ABER: Die Division ist in Z nicht uneingeschränkt durchführbar !
(-3) : 4 = -0,75 ∉ Z
Bsp.:
3. DIE MENGE DER RATIONALEN ZAHLEN(Q)
Q={
a
/ a ∈Z ∧ b ∈Z\{0}}
b
Echte Teilmengen:
Q+, Q-
Es gilt: Die Menge der rationalen Zahlen ist abgeschlossen gegenüber der Addition,
Multiplikation, Subtraktion und Division.
d.h.
a c
, ∈Q ⇒
b d
a c
+ ∈Q
b d
a c
− ∈Q
b d
a c
. ∈Q
b d
a c
: ∈Q
b d
AUSNAHME: Die Division durch Null ist nicht definiert !!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!
Beachte:
2 ist keine rationale Zahl !!
© HTBLA Vöcklabruck - STET
Zahlenbereiche
5
4. DIE MENGE DER REELLEN ZAHLEN (/R)
Die Menge der reellen Zahlen ist die Vereingung der Mengen aller rationalen (endliche oder
periodische Dezimalzahlen) und irrationalen (unendliche,nicht periodische Dezimalzahlen)
Zahlen.
Beachte: Die Wurzel aus einer negativen Zahl ergibt keine reelle Zahl !
5. DIE MENGE DER KOMPLEXEN ZAHLEN (C)
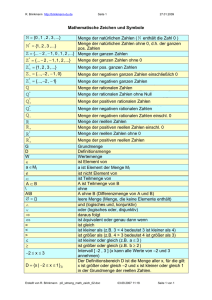
6. ÜBERSICHT ÜBER DIE ZAHLENBEREICHE
Menge der komplexen Zahlen (C)
Menge der reellen Zahlen ( /R)
Menge der rationalen Zahlen (Q)
Z
/N
{0}
Menge der irrationalen Zahlen
Q\Z
Z-
© HTBLA Vöcklabruck - STET