Ausführungen zu Exponentialfunktionen
Werbung
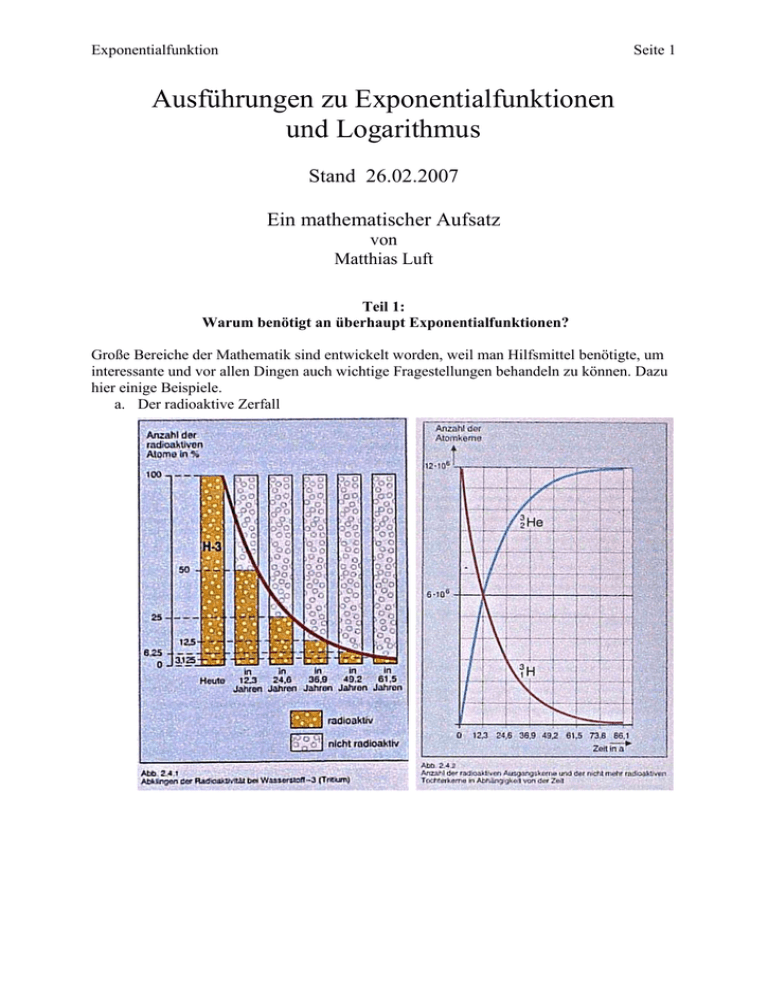
Exponentialfunktion Seite 1 Ausführungen zu Exponentialfunktionen und Logarithmus Stand 26.02.2007 Ein mathematischer Aufsatz von Matthias Luft Teil 1: Warum benötigt an überhaupt Exponentialfunktionen? Große Bereiche der Mathematik sind entwickelt worden, weil man Hilfsmittel benötigte, um interessante und vor allen Dingen auch wichtige Fragestellungen behandeln zu können. Dazu hier einige Beispiele. a. Der radioaktive Zerfall Exponentialfunktion Seite 2 b. Kettenreaktionen c. Medizinische Untersuchungen. Ein Beispiel. Um die Funktion der Bauchspeicheldrüse zu testen, wird ein bestimmter Farbstoff in sie eingespritzt und dessen Ausscheiden gemessen. Eine gesunde Bauchspeicheldrüse scheidet pro Minute etwa 4% des jeweils noch vorhandenen Farbstoffs aus. Bei einer Untersuchung wird dem Patienten 0,2 Gramm des Farbstoffs injiziert. Nach 30 Minuten sind noch 0,09 Gramm des Farbstoffs in seiner Bauchspeicheldrüse vorhanden. Ist diese Bauchspeicheldrüse gesund? d. Wachstumsprozesse. Auch hier ein Beispiel. Mal angenommen, in einem Streichelzoo befanden sich zu einem bestimmten Zeitpunkt 90 Meerschweinchen in einem Gehege. Ein Jahr später waren es bereits 120 Mehrschweinchen. Welche Meerschweinchenzahl ist in 10 Jahren zu erwarten, wenn man von einem linearen bzw. einem exponentiellen Wachstum ausgeht? Die Antwort zu der zu Beginn gestellten Frage lautet: All diese Vorgänge kann man mit Exponentialfunktionen hervorragend beschreiben. Exponentialfunktion Seite 3 Teil 2: Von Potenzen und Wurzeln Potenzen bestehen, so hat man schon früher gelernt, aus einer Basis und einem Exponenten. Die Potenz ist eine Kurzschreibweise für ein Produkt. Die Basis gibt dabei den Faktor an und der Exponent, wie oft dieser Faktor mit sich selbst multipliziert wird. So ist z.B. 25 2 2 2 2 2 . Man kann sich leicht überlegen, das es für das Rechnen mit Potenzen gewisse Regeln gibt. So findet man heraus, dass folgendes gilt: Re gel 1 a n a m a n m Re gel 2 a n b n ( a b) n Re gel 3 a 0 1 1 an Re gel 5 ( a n ) m a nm Re gel 4 a n Aufgabe: Kläre ab, welche Einschränkungen hier für die auftretenden Größen gelten. Es ist klar, dass durch Regel 4 die Möglichkeit gegeben ist, den Potenzbegriff auf Exponenten aus der Menge der ganzen Zahlen zu erweitern. Erweitern bedeutet, dass das, was man bisher schon wusste und kannte, nach wie vor seine Gültigkeit hat. Aber durch das Erweitern kommt neues Wissen hinzu. Und dieses neue Wissen muss zu dem alten Wissen „passen“. Es dürfen dadurch keine Widersprüche entstehen. Wie geht es aber weiter. Wir haben uns im Unterricht mit der Erweiterung des Wurzelbegriffs beschäftigt. Auch dort stellt man gewisse Regeln fest: n a n b n a b n m n a nm a an a Exponentialfunktion Seite 4 Aufgabe: Kläre ab, welche Einschränkungen hier für die auftretenden Größen gelten. Man kommt zu dem zunächst nicht unbedingt erwarteten Ergebnis, dass Wurzeln nicht anderes sind als spezielle Potenzen, wenn man folgende Notation festlegt n a a 1 n Damit ist der Weg nun frei zu definieren, was man unter einer Exponentialfunktion verstehen will. Es gilt Definition Eine Exponentialfunktion hat die Gestalt f ( x ) a0 a x Teil 3: Untersuchung von Exponentialfunktionen und ein Vergleich mit Potenzfunktionen. Diese Untersuchungen haben wir, genauer ihr, mit dem Programm Derive durchgeführt. Deshalb gestaltet sich dieser Teil hier als reiner Übungsteil. Exponentialfunktion Seite 5 Führe für diese Funktionsgraphen eine „Kurvendiskussion“ durch. Das bedeutet konkret: 1. Gib bei den vorliegenden Funktionen die Art der Symmetrie an und benenne die Symmetrieachse bzw. den Symmetriepunkt. 2. Gib jeweils drei Punkte an, die auf den Funktionsgrafen liegen. 3. Gib, so vorhanden, die Definitionslücken an. 4. Bestimme die Funktionsvorschriften und beschreibe, wir diese Graphen durch Verschieben aus anderen Graphen entstanden sind. 5. Beschreibe das Kurvenverhalten der gezeichneten Graphen. weitere Aufgabe Benenne Funktionen, die durch die folgenden Punkte verlaufen! a) (4/3) ; (5/2) ; (6/3) b) (4/1) ; (5/2) ; (6/1) c) (3/3) ; (4/4) ; (5/5) Wie geht es nun aber weiter? Diese Frage führt uns zu etwas, was einen ganz merkwürdigen Namen trägt. Wie kommen zu den Logarithmen. Teil 4: Existenz und Definition des Logarithmus Auch hier soll zunächst die Frage beantwortet werden, wozu man die Logarithmen überhaupt braucht. Dazu kommen wir noch einmal zu den Aufgabe mit den Meerschweinchen. Exponentialfunktion Seite 6 Mal angenommen, in einem Streichelzoo befanden sich zu einem bestimmten Zeitpunkt 90 Meerschweinchen in einem Gehege. Ein Jahr später waren es bereits 120 Mehrschweinchen. Welche Meerschweinchenzahl ist in 10 Jahren zu erwarten, wenn man von einem linearen bzw. einem exponentiellen Wachstum ausgeht? Funktionen ordnen verschiedene Dinge einander zu. Die Exponentialfunktion, die man zur Lösung dieser Aufgabe benutzt, ordnet verschiedenen Zeitpunkten verschiedene Anzahlen von Meerschweinchen zu. Also für einen gegeben Zeitpunkt erfährt man, wie viele Meerscheinchen da sind. Nun kann man diese Situation aber „umdrehen“. Wie lange muss man warten, um eine ganz bestimmte Anzahl von Meerschweinchen zu haben? Diese Antwort auf diese Frage beginnt mit der Zahl der Meerschweinchen und endet bei einem Zeitpunkt. Oder wie der Mathematiker sagen würde: Jeder Anzahl von Meerschweinchen wird ein Zeitpunkt zugeordnet. Als genau die umgekehrte Richtung wie bei der Exponentialfunktion. Damit ist das Ziel genannt. Es beginnt die Suche nach der Umkehrfunktion einer gegebenen Exponentialfunktion. Davon gibt es aber eine ganze Menge, wie wir hoffentlich gelernt haben. Denn für jede positive reelle Zahl a gibt es die Exponentialfunktion: f ( x) a x Also muss es auch eine ganze Menge von Umkehrfunktionen geben, wenn es sie denn überhaupt gibt! Betrachten wir z.B. die Funktion f 2 ( x ) 2 Den Index 2 bei f habe ich hier mal eingefügt, im Gegensatz zum Unterricht. Er soll lediglich deutlich machen, was die Basis dieser speziellen Exponentialfunktion ist. Betrachten wir nun das folgende Bild: x Exponentialfunktion Seite 7 Wie wir ja wissen, erhalte ich den Graphen der Umkehrfunktion, wenn ich den Ausgangsgraphen an der Normalgeraden ( also f(x)=x ) spiegle. Das geht hier offensichtlich. Also gibt es zu einer gegeben Exponentialfunktion eine Umkehrfunktion. Schreiten wir also zur Namensgebung, sprich Definition. Definition f a ( x ) a x die zugehörige Exponentialfunktion. Dann bezeichnet man mit log a ( x ) die zugehörige Es sei a eine positive reelle Zahl und Umkehrfunktion. Das ist alles. Es ist das erste Mal, dass wir hier eine Funktion kennen lernen, von der klar ist, dass es sie gibt aber von der wir nicht über einen Funktionsterm verfügen, wie bei den bisherigen Funktionen. Und doch werden wir einige „Rechenregeln“ dieser Funktion kennen lernen und sie auch beweisen. Als erstes machen wir uns klar, was es eigentlich bedeutet mit einer Funktion und ihrer Umkehrfunktion zu arbeiten. Nach Definition ( also nach Festlegung ihrer Eigenschaften ) bedeutet das Folgendes: Satz Für jede positive reelle Zahl a gilt: f a (log a ( x)) log a ( f a ( x)) x Sieht komisch aus, ist aber eigentlich klar. Hier gibt es nichts zu beweisen, da hier lediglich die Definition in Formelsprache aufgeschrieben worden ist. Wichtig ist hier auch noch etwas anderes. In vielen Büchern sieht die Definition des Logarithmus auf den ersten Blick ziemlich anders aus als hier. Etwa so: Definition Es sei a eine positive reelle Zahl und x und y zwei weitere reelle Zahlen, so dass gilt: a Gleichung. x y . Dann bezeichnet man mit x log a ( y ) die Lösung dieser Es ist ganz wichtig zu verstehen, dass die Definitionen auf dieser Seite völlig gleichwertig sind. Das Erspart einem viel Arbeit und sollte das Verstehen dieser Sachverhalte erleichtern. Teil 5: Rechenregeln für den Logarithmus Satz Es seien a und u reelle positive Zahlen und r eine reelle Zahl. Dann gilt log a (u r ) r log a (u) Beweis Exponentialfunktion Seite 8 Ganz ruhig bleiben. Man muss nur zwei Mal die Definition für den Logarithmus aufschreiben. Auf geht’s. Nach Definition des Logarithmus gilt: u a log a ( u ) und u r a log a ( u r ) Die erste Beziehung setzt man in die zweite ein und zwar auf der linken Seite. Dann erhält man die Gleichung rlog a ( u ) log a ( u r ) Dabei muss man lediglich die Potenzregel a a (a n ) m a nm anwenden. Damit ist dieser Beweis aber schon fertig. Wenn nämlich zwei Potenzen mit gleicher Basis übereinstimmen, da müssen ja wohl auch ihre Exponenten gleich sein. Es gilt also log a (u r ) r log a (u) . Es nächstes gehen wir nun die „Produktregel“ und die „Quotientenregel“ an. Dazu formulieren und beweisen wir einen weiteren Satz. Satz Es seien a, u und v positive reelle Zahlen. Dann gelten folgende Rechenregeln: log a (u v) log a (u) log a (v) u 2. log a ( ) log a (u ) log a ( v ) v 1. Beweis Auch hier wendet man konsequent die Eigenschaft der Umkehrfunktion an. Also da der Logarithmus die Umkehrfunktion zur Exponentialfunktion ist, gelten natürlich die folgenden Beziehungen: u a log a ( u ) log ( v ) 2. v a a log ( uv ) 3. u v a a 1. Man mache sich klar, dass da wirklich nur die Definition 3 Mal hingeschrieben worden ist. Und der Rest ist Einsetzen: log a (u v ) log a ( a log a ( uv ) ) log a ( a log a ( u ) a log a ( v ) ) log a ( a log a ( u ) log a ( v ) ) log a (u ) log a ( v ) Der Reihe nach. Das erste Gleichheitszeichen gilt, da hier die Eigenschaft „Umkehrfunktion“ benutzt wurde. Das zweite Gleichheitszeichen gilt, da hier die Beziehungen 1. und 2. für u und v eingesetzt worden sind. Das dritte Gleichheitszeichen beruft sich auf die Rechenregeln von Potenzen gleicher Basis und das letzte Gleichheitszeichen wiederum auf die Eigenschaft „Umkehrfunktion“ Der Beweis der Quotientenregel ist praktisch identisch. Man muss dazu lediglich die 2. Beziehung umformen und zwar so: Exponentialfunktion 2’. Seite 9 1 a log a ( v ) v da folg unmittelbar aus der Definition negativer Exponenten. Den Beweis kann man nun von der Produktregel fast abschreiben: u log a ( ) u v log a ( ) log a ( a ) log a ( a log a ( u ) a log a ( v ) ) v log a ( a log a ( u ) log a ( v ) ) log a (u ) log a ( v ) Soviel zu den Rechenregeln Teil 6: Eine für alle, alle für eine Hier soll nun klar gemacht werden, dass man in Wirklichkeit mit einer einzigen Logarithmusfunktion sch genug hat, denn man kann Logarithmusfunktionen und somit natürlich auch Exponentialfunktionen ineinander umrechnen. Und das ist gut so! Satz a und b seien positive reelle Zahlen. Dann gilt: log a ( x ) 1 log b ( x ) log b ( a ) Beweis: Beginnen wir mit der Beziehung : ay x Dann gilt einmal natürlich y log a ( x ) So ist der Logarithmus nun mal definiert. Es gilt aber auch und Verwendung des ersten Satzes zu Logarithmus: log b ( x) log b (a y ) y log b (a ) log a ( x) log b (a ) Die letzte Gleichung teilt man nun durch log b (a ) . Fertig!