Reaktionsgeschwindigkeit
Werbung
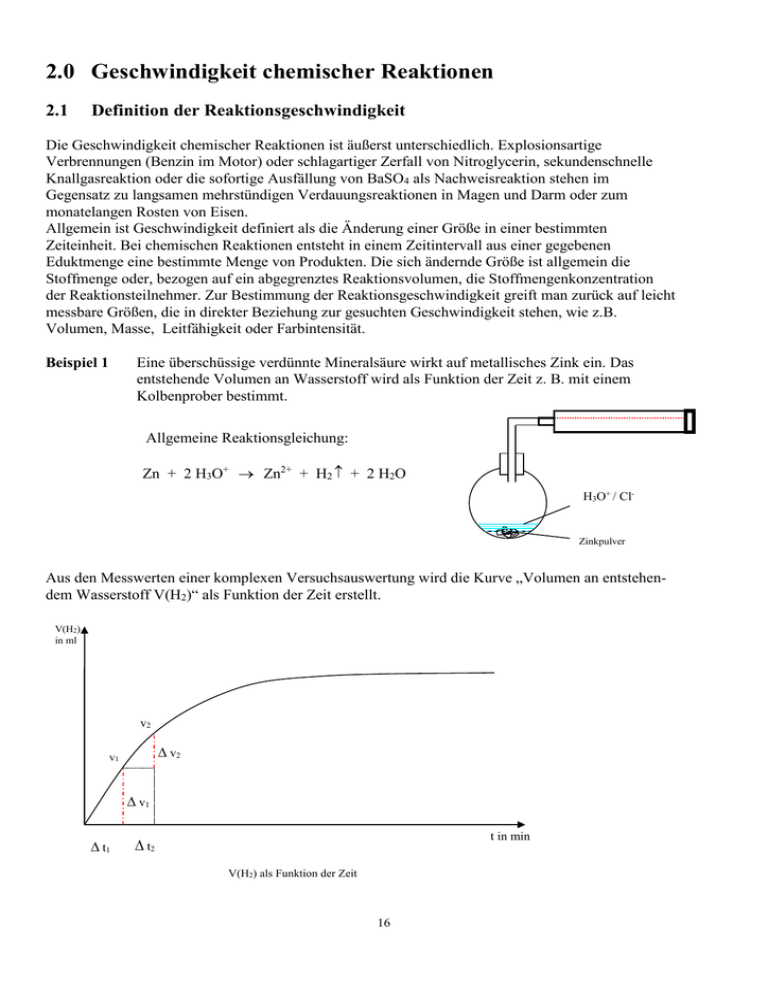
2.0 Geschwindigkeit chemischer Reaktionen 2.1 Definition der Reaktionsgeschwindigkeit Die Geschwindigkeit chemischer Reaktionen ist äußerst unterschiedlich. Explosionsartige Verbrennungen (Benzin im Motor) oder schlagartiger Zerfall von Nitroglycerin, sekundenschnelle Knallgasreaktion oder die sofortige Ausfällung von BaSO4 als Nachweisreaktion stehen im Gegensatz zu langsamen mehrstündigen Verdauungsreaktionen in Magen und Darm oder zum monatelangen Rosten von Eisen. Allgemein ist Geschwindigkeit definiert als die Änderung einer Größe in einer bestimmten Zeiteinheit. Bei chemischen Reaktionen entsteht in einem Zeitintervall aus einer gegebenen Eduktmenge eine bestimmte Menge von Produkten. Die sich ändernde Größe ist allgemein die Stoffmenge oder, bezogen auf ein abgegrenztes Reaktionsvolumen, die Stoffmengenkonzentration der Reaktionsteilnehmer. Zur Bestimmung der Reaktionsgeschwindigkeit greift man zurück auf leicht messbare Größen, die in direkter Beziehung zur gesuchten Geschwindigkeit stehen, wie z.B. Volumen, Masse, Leitfähigkeit oder Farbintensität. Beispiel 1 Eine überschüssige verdünnte Mineralsäure wirkt auf metallisches Zink ein. Das entstehende Volumen an Wasserstoff wird als Funktion der Zeit z. B. mit einem Kolbenprober bestimmt. Allgemeine Reaktionsgleichung: Zn + 2 H3O+ Zn2+ + H2 + 2 H2O H3O+ / Cl- Zinkpulver Aus den Messwerten einer komplexen Versuchsauswertung wird die Kurve „Volumen an entstehendem Wasserstoff V(H2)“ als Funktion der Zeit erstellt. V(H2) in ml v2 v2 v1 v1 t1 t in min t2 V(H2) als Funktion der Zeit 16 Konkretes Beispiel aus einem Experiment: Im ersten Zeitintervall von t0 bis t1 werden 11 ml Wasserstoff erzeugt bei 0 oC; diese entsprechen 10,25 ml Gas bei Normalbedingungen. Ein mol Wasserstoffgas nimmt idealisiert bei diesen Bedingungen 22,4 l ein. n(H2) = 1,025 10-2 l/ 22,4 mol/l Aus der Reaktionsgleichung folgt: = 4,58 10 4 mol n(H2) = n(Zn2+) Verteilt sich diese Stoffmenge z.B. auf 10 ml Lösung lt. den gegebenen Versuchsbedingungen, so ergibt sich für die Konzentration an Zn2+-Ionen zum Zeitpunkt t1: c1(Zn2+) = 4,58 10-4 mol / 1 10-2 l = 4,58 10-2 mol/l Für die Reaktionsgeschwindigkeit während des ersten Zeitintervalls t = 1 min (die Zink-IonenKonzentration zum Zeitpunkt t0 entspricht 0 mol/l) ergibt sich damit: v = (c1 - c0 ) : ( t1 - t0 ) = 4,58 10-2 mol/l : 1 min = 4,58 10-2 mol/ l min Beispiel 2 Auflösen von Marmor durch verdünnte Salzsäure. Kohlenstoffdioxid entweicht. Der Massenverlust des offenen Systems wird als Funktion der Zeit mit einer Waage bestimmt. CaCO3 + 2 H3O+ + 2 Cl- Ca2+ + 2 Cl- + CO2 + 3 H2O Reaktionsgleichung: Der Massenverlust durch Entweichen von Kohlenstoffdioxid lässt sich durch Stoffmengenbetrachtung aus der Reaktionsgleichung in die ansteigende Konzentration an Ca2+ umrechnen und dann entsprechend grafisch auftragen. Die entstehende Kurve (c(Ca2+))(t) ist mit der aus Beispiel 1 vergleichbar; sie nähert sich asymptotisch einer horizontalen Geraden, wenn z. B. der gesamte Marmor aufgelöst ist. Weitere Aufgaben Buch S. 117/1, 2; Bei allen chemischen Reaktionen treten Konzentrationsänderungen auf, auch wenn keine Volumenveränderungen zu registrieren sind. So ergibt sich folgende Definition: Def. : Die Reaktionsgeschwindigkeit einer chemischen Reaktion ist der Quotient aus der Konzentrationsänderung eines Stoffes und dem betrachteten Zeitintervall. v = c t (Einheit : mol/ l s ) Edukte und Produkte einer Reaktion sind über die Reaktionsgleichung miteinander verknüpft; zur Bestimmung der Reaktionsgeschwindigkeit genügt damit die Bestimmung der Konzentrationsänderung eines Reaktionsteilnehmers. Die so bestimmten Geschwindigkeiten sind immer Durchschnittsgeschwindigkeiten bezogen auf feste Zeitintervalle. Wählt man diese Zeitabschnitte immer kleiner ( t 0 s ), dann ergibt sich aus dem Differenzenquotient der entsprechende Differentialquotient, aus der Durchschnittsgeschwindigkeit entsteht im Grenzübergang die Momentangeschwindigkeit. Zum Zeitpunkt t gilt hierfür: 17 v = dc dt Im Konzentrations-Zeit-Diagramm entspricht der Durchschnittsgeschwindigkeit grafisch die Steigung der entsprechenden Sekante, der Momentangeschwindigkeit die Steigung der zugehörenden Tangente. c in mol/l c Momentangeschwindigkeit v zum Zeitpunkt t1 : vm dc = dt t Durchschnittsgeschwindigkeit in einem Intervall : vd c t c t t in sec V(H2) als Funktion der Zeit; Durchschnittsgeschwindigkeit; Momentangeschwindigkeit Der exakte gleichungsmäßige Zusammenhang zwischen der Reaktionsgeschwindigkeit und den augenblicklichen Konzentrationen aller an einer Reaktion beteiligter Substanzen lässt sich in Geschwindigkeitsgesetzen zusammenfassen und über verschiedene Reaktionsordnungen definieren. Sie sind kein Unterrichtsgegenstand der T-12-Chemie. 2.2 Aktivierungsenergie Die Geschwindigkeit chemischer Reaktionen wird beeinflusst von der Konzentration der Reaktionspartner, den Oberflächen reagierender Körper, der Temperatur und den sog. Katalysatoren. Der Einfluss der Konzentration ist in den Geschwindigkeitsgesetzen enthalten. Ein einfaches Beispiel für die Wirkung großer Oberflächen ist die unterschiedliche Reaktion von Eisen mit einer offenen Flamme. Ein kompakter Eisenstab kann in der Flamme erhitzt werden, ohne Feuer zu fangen. Feinverteiltes Eisenpulver dagegen verbrennt in der Luft, denn dem Angriff des Sauerstoffs wird eine viel größere Oberfläche geboten (vgl. Mehl- oder Kohlenstaubexplosionen, verursacht durch feinstverteilte, brennbare Substanzen und Zündung durch Funken). Def. : Die Aktivierungsenergie ist die Energie, die man einsetzen muss, damit eine chemische Reaktion mit merklicher Geschwindigkeit startet bzw. abläuft. Beispiel 1 Wasserstoff- und Sauerstoffgas im Verhältnis 2 : 1 reagieren bei Zimmertemperatur praktisch nicht miteinander. Bei Zündung des Gasgemenges durch eine Flamme oder 18 einen Funken stellt sich eine explosionsartige Reaktion ein. Beispiel 2 Feuergefährliches Benzin kann beim Tanken gefahrlos gehandhabt werden. Erst die Zündung im Verbrennungsraum setzt die enthaltene Energie frei. Chemische Systeme, wie z.B. Knallgas aus Beispiel 1 oder das Kraftstoff-Luft-Gemisch aus Beispiel 2, welche zu exothermen Reaktionen befähigt sind, diese aber nicht von sich aus eingehen können, heißen metastabile Systeme. Nach der vereinfachten Stoßtheorie reagieren Moleküle nur dann miteinander, wenn sie mit so viel kinetischer Energie geometrisch geeignet zusammentreffen, dass durch den Zusammenstoß Bindungen aufgebrochen werden (Kollisionsmodell). Die kinetische Mindestenergie für einen ausreichend kräftigen Zusammenstoß entspricht etwa der Aktivierungsenergie. Energie 4H, 2O Aktivierungsenergie EA 2H2, O2 freiwerdende Reaktionsenthalpie HR , HR < 0 2H2O Reaktionskoordinate Energie C6H12O6, 6O2 Aktivierungsenergie EA von außen aufzuwendende Reaktionsenthalpie HR HR > 0 6CO2, 6H2O Reaktionskoordinate Zusammenhang „Energie-Reaktionsfortschritt“ bei exothermen und endothermen Reaktionen 19 2.3 Konzentrationsabhängigkeit Versuch 1 Natriumthiosulfatlösung wird mit Salzsäure unterschiedlicher Konzentration versetzt. Es tritt eine Disproportionierung des Schwefels im Thiosulfat-Ion zu Schwefeldioxid und elementarem Schwefel ein (Redox-System als HA). Na2S2O3 + 2H3O+ + 2 Cl- S + SO2 + 3H2O + 2Na+ + 2 Cl- Die Natrium- und Chlorid-Ionen sind nur Begleitionen, da sie an der Umsetzung nicht beteiligt sind; die Reaktionsgleichung vereinfacht sich damit zu S2O32- + 2H3O+ S + SO2 + 3H2O Der zunächst als feine Trübung auftretende Schwefel ballt sich zu einem gelben Niederschlag zusammen. Die kürzere Reaktionszeit mit konzentrierterer Säure zeigt, dass die größere Konzentration an Oxonium-Ionen auch eine größere Reaktionsgeschwindigkeit bewirkt. c(H3O+)2 v Versuch 2 Eine Verdünnungsreihe mit unterschiedlicher Thiosulfat-Konzentration wird hergestellt und mit Salzsäure gleicher Konzentration versetzt. Die Reaktionszeiten verhalten sich etwa umgekehrt wie die Konzentrationen. v c(S2O32-) Für viele allgemeine Reaktionen vom Typ A + B C + D findet man, dass die Reaktionsgeschwindigkeit sowohl proportional c(A) als auch proportional c(B) ist. Dafür gilt dann: v = k c(A ) c( B) Geschwindigkeitsgesetz für die obige Reaktion k charakteristische Geschwindigkeitskonstante k ist stark temperaturabhängig großer Wert von k große Reaktionsgeschwindigkeit Aus den beiden obigen Versuchen ergibt sich damit: 2 v = k (c( H 3O )) 2 c(S 2 O3 ) A: B=1:1 A : B = 10 : 1 o o o o A : B = 10 : 10 o * o * o o * * o o * * o* *o o o * 1 o o : * o o 10 : o o * o * 100 Verhältnis der Zusammenstöße zwischen den Teilchen A und B in der gleichen Zeit und bei gleicher Temperatur Häufigkeit der Zusammenstöße von Teilchen 20 Eine Erhöhung der Ausgangskonzentration einer Komponente beschleunigt in vielen Fällen die Reaktionsgeschwindigkeit, eine eigentlich alltägliche Tatsache. Als Erklärung dieser Erkenntnis kann beispielhaft die Knallgasreaktion im Gasraum oder die obige Reaktion von Thiosulfat in Lösung herangezogen werden. Die Gasteilchen bzw. die Ionen der Edukte befinden sich in ständiger Bewegung und stoßen dabei laufend miteinander zusammen. Kollisionen von ausreichendem Impuls, bei denen die Teilchen die nötige Aktivierungsenergie besitzen (um die Bindung aufzubrechen bzw. die Hydrathülle zu durchstoßen), führen zu einer chemischen Reaktion. Die Wahrscheinlichkeit von Zusammenstößen und damit auch von wirksamen, im chemischen Sinn wirksamen Kollisionen steigt direkt mit der Zahl der Teilchen pro Volumeneinheit, also mit steigender Konzentration an. 2.4 Temperaturabhängigkeit Versuch Thiosulfatlösungen gleicher Konzentration werden mit verdünnter Salzsäure bei deutlich unterschiedlichen Temperaturen versetzt und die Zeitspanne bis zum Eintreten der Schwefel-Trübung verglichen. Bei höherer Temperatur tritt der Thiosulfatzerfall deutlich früher ein. Die Geschwindigkeit der Ionen in der Lösung und damit ihre kinetische Energie hat sich vergrößert und damit die Intensität der Zusammenstöße. Mehr Ionen werden damit aktiviert und reagieren bei geeignetem Aufprall mit entsprechenden Reaktionspartnern. Nach Arrhenius steigt die Reaktionsgeschwindigkeit mit erhöhter Temperatur. Nach einer Faustregel bewirkt eine Temperaturerhöhung um 10o eine Verdopplung der Reaktionsgeschwindigkeit; real sind Steigerungsraten zwischen Faktor 1,5 und 4,0. Eine Temperatursteigerung von 100o ergibt einen durchschnittlichen Faktor von 210 = 1024. Damit muss also auch die Geschwindigkeitskonstante k im Geschwindigkeitsgesetz größer werden. Genauer Zusammenhang : k = Ae EA R T mit EA R A T Aktivierungsenergie allg. Gaskonstante reaktionscharakteristische Konstante abs. Temperatur Nach den Untersuchungen von L. Boltzmann besitzen nicht alle Teilchen eines Gases (oder Ionen einer Flüssigkeit) identische kinetische Energie; eine große Anzahl von Molekülen wird eine mittlere, zur vorliegenden Temperatur passende Energie beinhalten, es werden aber auch sehr energiearme und energiereiche Moleküle existieren. Es ergibt sich die charakteristische Boltzmannverteilung der Anzahl der Teilchen als Funktion ihrer kinetischen Energie. 21 Zahl der Teilchen EA kinetische Energie Teilchenanzahl bei einer festen, vorgegebenen Temperatur als Funktion der kinetischen Energie der Teilchen Bei einer angenommenen Aktivierungsenergie EA sind bei einer gegebenen Temperatur T1 nur ein bestimmter Anteil der Moleküle bei einem Zusammenstoß zu einer Reaktion befähigt (Fläche unter der Kurve rechts von EA). Bei einer höheren Temperatur T2 verschieben sich das Kurvenmaximum und der asymptotische Kurvenauslauf nach rechts mit einem deutlichen Anstieg der Teilchenzahl mit kinetischer Energie größer als EA (rot schraffierter Bereich). Der Ordinatenwert des absoluten Maximums muss sich in der Kurve für die höhere Temperatur verkleinern wegen der Forderung der Flächengleichheit (gleiche Teilchengesamtzahl). Zahl der Teilchen EA kinetische Energie Verteilung der Energie auf die Teilchen eines Systems bei verschiedenen Temperaturen. 22 2.5 Abhängigkeit vom Zerteilungsgrad Metallisches Zink wird bei Raumtemperatur mit verdünnter Salzsäure versetzt. Das Metall wird in unterschiedlichen Korngrößen eingesetzt, von Zn-Staub, Zn-Pulver, Zn-Körnern, Zn-Granalien bis zu einem Zn-Brocken. Die Intensität der Wasserstoffentwicklung sinkt mit steigender Korngröße. Die Reaktionsgeschwindigkeit ist proportional zur Oberfläche des Metalls; nur an der Außenschicht kann eine Reaktion mit den Oxonium-Ionen stattfinden. Diese Abhängigkeit ist auf Oberflächen-Reaktionen (i. A. Festkörperbeteiligung) beschränkt. 2.6 Abhängigkeit vom Druck Bei Reaktionen unter Beteiligung von Gasen kann eine Druckveränderung Einfluss auf den Ablauf einer Reaktion bewirken. Hierzu ist die konkrete Reaktionsgleichung zu betrachten. Nur Reaktionen mit unterschiedlicher Zahl der Stoffmengen an Gasen auf der Edukt- und der Produktseite reagieren auf Druckvariation. Volumenvermindernde Reaktionen werden durch Druckerhöhung begünstigt, Reaktionen mit Volumenvergrößerung durch Druckreduzierung. Beispiel Großtechnische Ammoniakdarstellung aus den Elementen 3 H2 + N2 4 Mol Gase 2 NH3 2 Mol Gase Das Anlegen eines Überdrucks (technisch z. B. 200 bar) begünstigt die Entstehung von Ammoniak. Übungsbeispiele Aufgabe 1 Kupferspäne reagieren bei Raumtemperatur mit halbkonzentrierter Salpetersäure. Als Gas entsteht zunächst Stickstoffmonoxid, Cu2+-Ionen sind in der Lösung nachweisbar. Das farblose Gas NO reagiert mit Luftsauerstoff bei Raumtemperatur zu NO2. Reaktionsgleichung: 3Cu + 8H3O+ + 8NO-3 3Cu(NO3)2 + 2NO + 12H2O Es werden nun verdoppelt: a) b) c) d) die Temperatur, das Volumen der Säure, die Konzentration der Säure, der Druck auf die Flüssigkeitsoberfläche. Begründen Sie die Wirkung dieser Maßnahmen bzgl. der Reaktionsgeschwindigkeit. Aufgabe 2 Konzentrierte Salzsäure reagiert mit Aluminiumkörnern unter Wasserstoffentwicklung. Reaktionsgleichung : 6H3O+ + 6Cl- + 2Al 2AlCl3 + 3H2 + 6H2O Durch welche sinnvollen äußeren Veränderungen lässt sich die Reaktionsgeschwindigkeit erhöhen? Genaue Begründungen! 23 2.6 Katalyseabhängigkeit Bei einigen Reaktionen wird die Geschwindigkeit durch die Zugabe kleiner Mengen bestimmter Substanzen beschleunigt; oft liegen diese Stoffe nach der Reaktion unverändert vor. Substanzen mit dieser Eigenschaft heißen Katalysatoren. Def. : Ein Katalysator ist eine Substanz, die die Reaktionsgeschwindigkeit einer chemischen Reaktion erhöht, ohne selbst bei der Reaktion verbraucht zu werden. Im Chinesischen bedeutet das Wort Katalysator eigentlich „Heiratsvermittler“. Ein Katalysator reduziert die Aktivierungsenergie EA einer Reaktion; so kann eine größere Anzahl von Molekülen die EA-Barriere überwinden und es kommt zu einer merkbaren Produktbildung. Energie Aktivierungsenergie EA ohne Katalysator Aktivierungsenergie EA mit Katalysator Edukte ( 2 H2, O2 ) ( H = -286 kJ/mol ) Produkte ( 2 H 2O ) Reaktionsfortschritt Katalysatoreinfluss auf die Aktivierungsenergie einer exothermen Reaktion Beispiel 1 Knallgasreaktion von Wasserstoff und Sauerstoff zu Wasser , Pt 2 H2O H = -286 KJ/mol 2 H2 + O2 RT Wasserstoff und Sauerstoff sind bei Raumtemperatur ein metastabiles Gasgemenge. Ohne Aktivierung durch „Zündung“ findet praktisch keine Reaktion statt. Durch Hinzufügen von feinst verteiltem Platin (Platinasbest) verläuft die Reaktion der Wasserbildung bei Raumtemperatur merklich aber nicht explosiv ab. Damit erreichen bzw. überschreiten ausreichend viele Moleküle die jetzt deutlich niedrigere Aktivierungsenergie und die Reaktion kommt in Gang. Dies ist eine Folge der Oberflächenwirkung des Metalls. An den Metallatomen an der Oberfläche sind noch Valenzen frei, die mit benachbarten Wasserstoffmolekülen wechselwirken. Damit wird die Atombindung im Gasmolekül gedehnt bis vollständig gespalten, es entstehen an Platin schwach gebundene 24 Wasserstoffatome. Diese können an der Katalysatoroberfläche bei Aufprallen von Sauerstoffatomen lokal spontan reagieren zu Wasser. Die Wassermoleküle lösen sich sofort von der Metalloberfläche, die nun für eine neue Katalyse zu Verfügung steht. O2 H2 H2 freie Valenzen von Pt Pt-Katalysator-Oberfläche Wirkungsweise von oberflächenaktivem Platin bei der stillen Knallgasreaktion Beispiel 2 Katalytische Beschleunigung der thermischen Zersetzung von Kaliumchlorat durch eine geringe Menge an Braunstein: MnO 2 2KClO3 (s) , Beispiel 3 2KCl (s) + 3O2 (g) Die thermische Zersetzung von Wasserstoffperoxid ist stark temperaturabhängig; bei Raumtemperatur und Dunkelheit ist die Zerfallsgeschwindigkeit sehr klein. Ein kleiner Zusatz von Braunstein ergibt sofort eine heftige Gasentwicklung nach: 2H2O2 (aq.) 2H2O (l) + O2 (g) H = -196,3 kJ/mol Der Braunstein lässt sich nach beendeter Reaktion in unveränderter Menge isolieren und auch wieder erfolgreich einsetzen (Heterogenkatalysator). Die Zugabe von Chromat-Ionen (im neutralen bis leicht saurem Milieu) zu einer Wasserstoffperoxidlösung zeigt ebenfalls eine (leicht verzögerte) Zerfallsreaktion. Die Gelbfärbung durch die Chromat-Ionen verdunkelt sich, ein blauvioletter Übergangskomplex entsteht: HCrO4- + 2 H2O2 gelb HCrO6- + 2 H2O blauviolett Dieser Farbkomplex (eigentlich ein Hydroxy-Komplex [CrO5(OH)]- ) spaltet Sauerstoff ab und wird wieder zur gelben Ausgangsverbindung: HCrO6- HCrO4- + O2 Die Chromat-Ionen entstehen nach diesem Kreisprozess unverändert, es liegt eine homogene Katalyse vor. 25 Ein weiterer Homogenkatalysator für die Wasserstoffperoxid-Zersetzung ist elementares Brom. Das Halogen ist fein verteilt in der wässrigen Phase und wirkt über einen bekannten Reaktionsmechanismus: Br2 (aq) + H2O2 (aq) + 2H2O (l) 2Br- (aq) + 2H3O+ (aq) + O2 (g) 2Br- (aq) + H2O2 (aq) + 2H3O+ (aq) Br2 (aq) + 4H2O (l) Die Addition der beiden Teilschritte ergibt die obige Zersetzungsgleichung, die Brommoleküle und die Bromid-Ionen „kürzen“ sich weg, haben so zwar an der Reaktion teilgenommen, liegen aber in unveränderter Form und Menge wieder vor. Auch ein Zusatz von Hefe wirkt als Reaktionsbeschleuniger; Hefezellen enthalten einen Katalysator, der ebenfalls den Wasserstoffperoxid-Zerfall begünstigt. Katalysatoren, die Stoffwechselreaktionen in Organismen ermöglichen, werden als Biokatalysatoren oder Enzyme bezeichnet. Auch die Katalase, ein in der Kartoffel enthaltenes Enzym, lässt die Sauerstoffentwicklung in obiger Reaktion bei Raumtemperatur sofort merklich einsetzen (Biokatalysator). Beispiel 4 Technische Ammoniaksynthese aus den Elementen durch feinverteiltes Eisen, Aluminiumoxid und Kaliumoxid (Haber-Bosch-Synthese) katalysiert (Kontaktkatalyse). , Al 2 O 3 , K 2 O N2 (g) + 3H2 (g) Fe H <0 2NH3 (g) Das Eisen wirkt als Heterogenkatalysator durch zunehmende Dehnung der Stickstoff-Bindung über den Einfluss freier Valenzen des Metalls auf die Dreifachbindung. N2 3 H2 H H H H H N N N N H H H N N NH3 NH3 H2N NH2 Katalytische Wirkungsweise von Eisen bei der Ammoniaksynthese Heterogen-Katalysatoren befinden sich in einer anderen Phase als die Edukte und Produkte. Häufig handelt es sich hierbei um oberflächenaktive Festkörper, die bei Reaktionen in der Gasphase oder in Flüssigkeiten Verwendung finden. 26 Beispiel 5 Großtechnische Schwefelsäuresynthese nach dem Kontaktverfahren aus Schwefeldioxid und Sauerstoff mit Vanadiumpentaoxid. 2SO2 (g) + O2 (g) 2SO3 (g) H <0 V 2O 5 Bei Raumtemperatur reagieren Schwefeldioxid und Sauerstoff praktisch nicht miteinander und bei höherer Temperatur wird der Zerfall von Schwefeltrioxid begünstigt. Somit muss ein Katalysator eingesetzt werden. Beim Kontaktverfahren kommt Vanadiumpentaoxid auf Siliziumdioxid als Trägermaterial zum Einsatz. V2O5 + SO2 2 V2O4 + O2 V2O4 + SO3 2 V2O5 Der Katalysator wird mit Sauerstoff regeneriert und der Valenzwechsel vom V-wertigen zum IVwertigen Metalloxid rückgängig gemacht. Das entstehende Schwefeltrioxid (sehr schlecht wasserlöslich) löst sich gut in konzentrierter Schwefelsäure unter momentaner Bildung von Dischwefelsäure; diese wird durch permanente Wasserzugabe hydrolysiert zu konzentrierter Schwefelsäure: SO3 + H2SO4 H2S2O7 H2S2O7 + H2O 2 H2SO4 Die heterogenen Katalysatoren adsorbieren die reagierenden Substanzen an ihrer Oberfläche und führen damit zu einer Dissoziation oder zumindest zu einer Dehnung von Bindungen oder gar zu ihrer Spaltung und damit zu einem erleichterten Reaktionsablauf. Die gebildeten Substanzen müssen die Katalysatoroberfläche schnell verlassen, um Platz für erneute Katalyse zu machen. Katalysatoren beschleunigen i.a. nicht nur die Reaktion zu den Produkten, sondern begünstigen in Gleichgewichtsreaktionen auch die unerwünschte Rückreaktion. Die technische Lösung ist die Steuerung in die bevorzugte Richtung durch Entzug eines der Produkte z.B. durch Ausfällen oder durch sofortige Weiterreaktion oder durch Prozessführung mit einem (billigen) Edukt in leichtem Überschuss. 2.7 Technisch wichtige Katalysatoren In der Aufstellung sind einige wichtige Verfahren mit dem Einsatz von Katalysatoren aus der anorganischen und organischen Chemie im großtechnischen Einsatz aufgeführt. 27 Verfahren Ausgangsstoffe Produkte Katalysatoren Hydrierung Alkene, H2 z. B. CnH2n Alkane z. B. CnH2n+2 Raney-Nickel Pd, Pt Fischer-TropschVerfahren CO, H2 CnH2n + 2 Eisencarbid, Co Methanol-Synthese CO, H2 CH3OH ZnO / Cr2O3 Haber-BoschVerfahren N2 , H2 NH3 Fe / Al2O3 / K2O Epoxidierung Alkene, O2 C C Ag O Schwefelsäuredarstellung SO2 , O2 SO3 V2O5 Polymerisation Alkene Polymere Ni- , Ti- , V-Verb. Veresterungen Alkohole, Säuren Ester Schwefelsäure Autoabgaskatalysator Auch in „alltäglichen“ chemischen Reaktionen werden zunehmend Katalysatoren eingesetzt, v.a. in Kraftfahrzeugen. Sie sollen für die (fast) vollständige Oxidation bzw. für die Überführung von Schadstoffgasen in ungefährliche Substanzen sorgen. Kohlenmonoxid und unverbrannte Kohlenwasserstoffe werden zu Kohlendioxid oxidiert, Stockoxide zu Stickstoff reduziert. N2 + 2CO2 2NO + 2CO 2CO + O2 CxHy + (x + y 4 2CO2 ) O2 xCO2 + y 2 H2O (Folie: Aufbau Dreiwegekatalysator) Die katalytisch wirkende Schicht im Keramikwabenkörper (Al2O3 und CeO2) eines AutoKatalysators besteht aus ca. 2 g Edelmetallen wie Platin (Oxidationskatalysator), Palladium und Rhodium (Reduktionskatalysator); die Wirksamkeit liegt bei ca. 90% und ist stark vom Alter des Katalysator und der Fahrweise abhängig. Im Betrieb muss stets die Mischung von Benzin und Luft stimmen. Die Lambda-Sonde misst den Sauerstoffgehalt im Abgas und sorgt für eine elektronisch gesteuerte optimale Gemischzusammensetzung. Sie besteht aus einer Keramik mit den Wirkbestandteilen ZrO2 und Y2O3. In dieser Metalloxidschicht machen nicht besetzte Oxidfehlstellen 28 im Gitter eine O2- Ionenleitung möglich. Es entstehen damit messfähige Potentialdifferenzen, über die die Luftzufuhr im Vergaser elektronisch gesteuert wird. Luftseite : O2 + 4e- 2 O2- (Pluspol) Abgasseite: 2 O2- O2 + 4e- (Minuspol) Folie: Lambda-Fenster Das optimale Verhältnis von angesaugter Luftmasse zu theoretisch erforderlicher Luftmasse ( =1) wird nur in Grenzen erreicht. Bei <1 ist zu wenig Luft vorhanden (fettes Gemisch; Höchstlast mit = 0,9 – 095; extrem hoher NOx-Anteil, rel. niedrige CO- und KW-Anteile), bei >1 ist das Gemisch mager (geringster Kraftstoffverbrauch bei = 1,15 – 1,25; rel. niedriger NOx-Anteil, hohe CO- und KW-Anteile). Schwankungen bei Lastwechsel lassen sich nur träge nachregeln. Die Edelmetalle liefern kurzzeitig Sauerstoff bzw. entnehmen diesen aus dem Abgas und sorgen so für einen rascheren Ausgleich. Bei moderater Fahrweise stellt sich so ein -Fenster knapp unter dem Optimum Eins ein mit einem sinnvollen (für ihre möglichst vollständige Beseitigung; v. a. genügend hoher CO-Anteil für die Entstickung) Verhältnis der Schadstoffgase. Regelung der Luftzufuhr Vergaser Luft Dreiwege-Katalysator Motor Auspuff LambdaSonde Benzin Weitgehend gereinigtes Abgas Schematischer Aufbau der Abgasanlage eines Benzin-PKWs Probleme treten auch bei kaltem Motor auf, da hier das Emissionsproblem besonders groß und die Wirksamkeit des Katalysators klein ist. Diese Abgasentgiftung ist nur bei bleifreiem Benzin (kein Zusatz von Bleitetraethyl als Antiklopfmittel) möglich; Blei würde die Katalysatorenoberfläche blockieren und damit die Wirkungsweise praktisch vollständig verhindern. Der im Benzin enthaltene Schwefel ist ein zusätzliches Problem, denn Schwefel wird von den eingesetzten Edelmetallen bei den herrschenden Bedingungen von SO2 zu SO3 katalytisch oxidiert. Mit dem entstehenden Wasserdampf im Abgas entsteht analog der großtechnischen Produktion Schwefelsäure! (Siehe auch Buch S. 129f) Fallbeispiel Ein Mittelklassewagen verbraucht 7,0 l Benzin auf 100,0 km bei gemäßigter Fahrweise. Die Abgasmenge Kohlenstoffdioxid lässt sich unter der Annahme einer vollständigen Verbrennung und der Vereinfachung Modellbenzin entspricht Oktan ( = 0,7028 kg/l) berechnen. 2 C8H18 + 25 O2 16 CO2 + 18 H2O 29 7,0 Liter Oktan entsprechen 4,92 kg Modellbenzin. Mit der Molmasse 114,0 g/mol ergeben sich 43,2 mol Oktan. Nach der Reaktionsgleichung entstehen aus 2 mol Oktan 16 mol Kohlenstoffdioxid und damit als 345,6 mol CO2. Mit Avogadro (ein Mol Gas besitzt bei 25,0 0C ein Volumen von ca. 24,0 l) folgt ein CO2-Volumen von ungefähr 8295 l. Die Abgase eines benzingetriebenen Kraftfahrzeugs bestehen v. a. aus Stickstoff, Wasserdampf und Sauerstoff. Von 100,0 l Abgas sind ungefähr 10,0 l Schadstoffgase. Die Tabelle zeigt die durchschnittliche prozentuale Zusammensetzung der Schadgase eines Ottomotors ohne Katalysator. Ungefähre Zusammensetzung der schädlichen Kfz-Abgase in Vol% CO2 CO NOx SO2 CxHy Aldehyde 87,6 10,3 0,6 (gemäßigter Fahrstil) 0,06 1,07 (unverbrannte und teilverbrannte Kohlenwasserstoffe 0,4 Nach der Tabelle werden real nicht 8295 l Kohlenstoffdioxid, sondern nur 7422,3 l CO2 und zusätzlich 872,7 l CO freigesetzt. Die restlichen Schadgase entsprechen 2,1 Vol%. Ein Volumenprozent der Schadstoffgase entspricht 87,729 l. Damit sind die Volumen aller Schadstoffe berechenbar die bei einer 100,0 km Fahrt entstehen. Volumen der Schadstoffgase bei 100,0 km Fahrt in Vol% Volumen in l CO2 CO NOx SO2 CxHy Aldehyde 7422,3 872,7 50,8 5,1 90,7 33,9 87,6 10,3 0,6 (gemäßigter Fahrstil) 0,06 1,07 (unverbrannte und teilverbrannte Kohlenwasserstoffe 0,4 Setzt man vereinfacht wieder eine vollständige Verbrennung der 43,2 mol Oktan voraus, so ergibt sich ein Sauerstoffverbrauch von ungefähr 540 mol oder 12960 l O2 bei 25,0 0C. Unter der Annahme, dass Luft ca. 20 % Sauerstoff enthält, ergibt sich ein Luftverbrauch von 64800 l oder 64,8 m3 bei einer 100,0 km langen Fahrt. Der Durchsatz eines Triebwerks bei einem Düsenjet ist ungefähr in der gleichen Größenordnung, allerdings in einer Sekunde, kaum mit „gemäßigtem Fahrstil“ und ganz ohne Katalysator! Biokatalysatoren Auch im menschlichen Körper wirken v.a. Blei, Cadmium, Quecksilber und andere Schwermetalle als Katalysatorengifte; sie blockieren das aktive Zentrum eines Enzyms durch Deformation oder dauerhafte Besetzung, behindern damit seine Wirksamkeit und führen zu Vergiftungserscheinungen. Auch Nervengase blockieren enzymatisch kontrollierte Reaktionen und unterbrechen damit die Leitung von Nervenimpulsen. 30











