sta5verteil

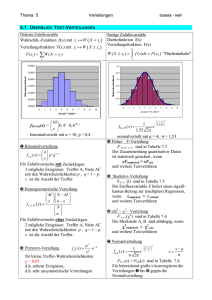
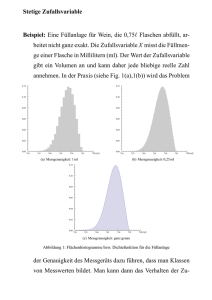
Thema 5
Verteilungen
Statistik - Neff
5.1 Ü BERBLICK T EST -V ERTEILUNGEN
Diskrete Zufallsvariable
Wahrschlk.-Funktion f(xi) mit xi
W  X  xi 
Verteilungsfunktion F(xi) mit xi
W  X  xi 
F ( xi )  W ( X  xi )
Stetige Zufallsvariable
Dichtefunktion f(x)
Verteilungsfunktion F(x)
W ( X  x2 ) 
x2

f ( x)dx  F ( x2 ) "Flächeninhalte"

i
0,3000
Wahrscheinlichkeit
0,2500
0,2000
0,1500
0,1000
0,0500
0,0000
0
1
2
3
4
5
6
7
8
9
10
Anzahl "Treffer"
10 
f10 | 0,4(x) =   0, 4 x  0, 610 x
x 
binomialverteilt mit n = 10, p = 0,4
1 Binomialverteilung
n
f n , p ( x)    p x q n  x
 x
Für Zufallsversuche mit Zurücklegen.
2 mögliche Ereignisse: Treffer A, Niete A
mit den Wahrscheinlichkeiten p , q = 1 – p.
x ist die Anzahl der Treffer.
2 Hypergeometrische Verteilung
 M  N  M 
 

x  n  x 

f n , N , M ( x) 
N
 
n 
Für Zufallsversuche ohne Zurücklegen.
2 mögliche Ereignisse: Treffer A, Niete A
mit den Wahrscheinlichkeiten p , q = 1 – p.
x ist die Anzahl der Treffer.
µx 
f µ ( x) 
e
3 POISSON-Verteilung
x!
für kleine Treffer-Wahrscheinlichkeiten
p < 0,05
d.h. seltene Ereignisse,
d.h. sehr unsymmetrische Verteilungen
1  x4 
2
 

1
f 4|1,55 ( x) 
e 2  1,55 
1,55 2
normalverteilt mit µ = 4, = 1,55
4 Fisher – F-Verteilung
F  | p |  | x sind in Tabelle 7.3
Der Zusammenhang quantitativer Daten
ist statistisch gesichert, wenn
xFempirisch > xFcrit.
und weitere Testverfahren
5 Student-t-Verteilung
F |  (t) sind in Tabelle 7.5
Die Einflussvariable X liefert einen signifikanten Beitrag zur (multiplen) Regression,
wenn tempirisch > t critical
und weitere Testverfahren
6 chi2   Verteilung
F  | (2) sind in Tabelle 7.4
Die Merkmale A, B sind abhängig, wenn
2empirisch > 2crit.
und weitere Testverfahren
7 Normalverteilung
1  x µ 
2
 

xµ
1
z
fµ|σ ( x) 
e 2 σ 
σ
σ 2π
F0 | 1(z) = FSN(z) sind in Tabelle 7.6
Für hinreichend große n konvergieren die
Verteilungen 1 bis 6 gegen die
Normalverteilung.
Thema 5
Verteilungen
Statistik - Neff
5.2 BERNOULLI-K ETTEN
Im Modell für Zufallsversuche "Werfen von Reißnägeln" gibt es zwei mögliche Ereignisse:
"Spitzenlage" s und "Rückenlage" r , s sei ein Treffer,  sei ein Nicht-Treffer.
Die Treffer-Wahrscheinlichkeit ist p, die für Nicht-Treffer ist q = 1 – p.
Bei Zufallsversuchen mit Zurücklegen bleiben die Wahrscheinlichkeiten p und q konstant.
Die Ereignisse einer Kette solcher Zufallsversuche sind voneinander unabhängig.
entspricht "Ziehen mit Zurücklegen"
Ketten unabhängiger Zufallsversuche mit jeweils zwei möglichen Ereignissen nennt man
BERNOULLI-Ketten. (Gutware | Ausschuss, ja | nein, positiv | negativ, bestanden | nicht best. …)
[BERNOULLI, Jakob, Basel 1713]
Aus den Zufallsversuchen (Abschnitt 3.9) kennen wir die Wahrscheinlichkeit dafür, dass ein
geworfener Reißnagel auf der Spitze liegt: p = W(X) = W(s) = 0,39 und q = 1– p = 0,61.
Die Zufallsvariable X ist die Anzahl der Treffer (Spitzenlage).
Wirft man 2-mal einen Reißnagel, dann ergeben sich die Möglichkeiten:

s
s
ss
X=
0
1
1
2
W(X) = q·q
q·p
p·q
p·p
und q2 + 2 q p + p2 = (q + p)2 = 1
Wirft man 3-mal einen Reißnagel, dann ergeben sich die Möglichkeiten:

 s, s, s 
ss, ss, ss
sss
X=
0
1
2
3
W(X) = q·q·q
3 q2·p
3 q·p2
p3
3 0
2
2
3
3
2
2
3
3
und
q p + 3 q p + 3 q p + p = p + 3 p q + 3 p q + q = (p + q) = 1.
Die Wahrscheinlichkeiten der BERNOULLI-Ketten folgen der Binomialentwicklung (p+q)n.
Z.B. Wahrscheinlichkeit für 2 Treffer W(X=2) = 3 p2 q = 3 · 0,392 · 0,61 = 0,278.
Wiederholung zu Binomialkoeffizienten siehe Abschnitt 5.5
n
n
Binomialverteilung: W(X = x) =fBin,n,p(x) =   p x q n  x    p x (1  p)n  x
 x
 x
x
n-x
p Wahrscheinlichkeit der x Treffer, (1–p) Wahrscheinlichkeit der n – x Nicht-Treffer.
(Multiplikationsregel für unabhängige Ereignisse, Abschnitt 4.2)
n
  gleichwahrscheinliche Kombinationen (Additionsregel für unabh. Ereignisse, vgl. 4.2)
 x
Der Erwartungswert µ = np, das ist unmittelbar einsichtig.
Für die Varianz gilt 2 = n p q. (siehe 5.4)
Die Binomialreihe für Treffer-Wahrscheinlichkeit p, Stichprobenumfang n:
n
n
n
 n
 n
( p  q) n    p 0 q n    p1q n 1    p 2 q n 2  ...    p x q n  x  ...    p n q 0  1
0
1 
2
 x
 n
Wahrscheinlichkeit für genau x Treffer:
n
fn,p(x) =   p x q n  x
 x
mit x = 0, 1, 2, …, n
Die Verteilungsfunktion liefert die aufsummierten Werte der Binomialverteilung:
k
k
n
FBin | n | p (k )   f n , p ( x)    p x q n  x
Tabelle 7.1
x 0
x 0  x 
Thema 5
Verteilungen
Statistik - Neff
5.3 B INOMIALVERTEILUNG
Beispiel 5.1
In einer Klinik werden in einem Monat n = 50 Geburten registriert.
Die Wahrscheinlichkeit für Mädchen ist p = 0,486.
a) Wie groß ist die Wahrscheinlichkeit dafür, dass darunter 20 Mädchengeburten sind? genau!
b) Wie groß ist die Wahrscheinlichkeit dafür, dass darunter höchstens 20 Mädchengeburten sind?
c) Erwartungswert, erwartete Varianz und erwartete Standardabweichung?
d) Wie ändert sich die erwartete Standardabweichung, wenn man das Stichprobenmittel aus
einem Jahr betrachtet?
q = 1 – 0,486 = 0,514 ist die Wahrscheinlichkeit für die Geburt eines Jungen.
 50 
50!
a) f Bin |50| 0,486 (20)    0, 48620  0,51430 
0, 486 20  0,51430  0, 0543  5, 4%
20!30!
 20 
20 50
 
b) FBin | 50 | 0,486 (20)     0, 486 x  0,51450 x 
x 0  x 
 50 
 50 
 50 
0
50
1
49
20
30
  0, 486  0,514    0, 486  0,514  ...   0, 486  0,514  0,141  14,1%
0 
1 
 20 
Das ist sehr aufwendig; man hat zwei Möglichkeiten
(1) ein Numerik-Programm benutzen z.B. in Excel: =BINOMVERT(20;50;0,486;1)
(2) mit Hilfe der Normalverteilung den Näherungswert bestimmen, siehe unten
Tabellen für FBin(k) gibt es nur für glatte p und n, hier etwa für p=0,5 und n=50.
c) µ = n p = 50 · 0,486 = 24,3 Mädchen
2 = n p q = 50 · 0,486 · 0,514 = 12,49
 = √12,49 = 3,53 Mädchen
σ
3,53
d) σ x 

 1,02 Mädchen
12
12
Beispiel 5.2
An einem erosionsgefährdeten Hang sollen 10 Fichtenpflanzen angepflanzt werden.
Die Baumschule gibt eine Anwachswahrscheinlichkeit von p = 40% an.
Wie groß ist die Wahrscheinlichkeit, dass
a) genau 4 b) höchstens 3 c) mindestens 5 d) alle 10 anwachsen?
e) Bestimmen Sie µ, 2, . f) Zeichnen Sie das Histogramm
Aus Tabelle 7.1
a) f(4) = F(4) – F(3) =
= 0,6331 – 0,3823 =
= 0,2508
b) F(3) = 0,3823
c) W(X ≥ 5) = 1 – F(4) =
=1 – 0,6331 = 0,3669
d) "genau 10" W(X = 10) =
= f(10) = F(10) – F(9) =
= 1 – 0,9999 = 0,0001
e) µ = 10·0,4 = 4 Fichten.
2 = 10·0,4·0,6 = 2,4 < 9
 = √2,4 = 1,55 Fichten

Thema 5
Verteilungen
Statistik - Neff
5.4 V ARIANZ  2 = n p q
Varianz einer binomialverteilten Zufallsvariablen
Für die Varianz einer Zufallsvariablen gilt:
2   xi2  f ( xi )  µ2
i
Speziell für Binomialverteilung:
Bei 1 "Wurf": n = 1
n 
2   xi2    p xi q n xi  (np)2
i
 xi 
1 
 1
W ( X  0)    p 0 q1 und W ( X  1)    p1q 0
 0
 1
1 
 1
2  02   p 0 q1  12   p1q 0  (1 p)2  p  p 2  p(1  p)  1 pq
0
 1
Bei 2 "Würfen": n = 2
X = 0; 1; 2 W(X=0); W(X=1); W(X=2)
 2
 2
 2
2  02   p 0 q 2  12   p1q1  22   p 2 q 0  (2  p)2  1 2  pq  4 1 p 2  4 p 2  2 pq
0
1 
 2
Bei 3 "Würfen": n = 3
X = 0; 1; 2; 3
W(X=0); W(X=1); W(X=2); W(X=3)
3
 3
3
 3
2  02   p 0 q 3  12   p1q 2  22   p 2 q1  32   p 3q 0  (3  p )2  3 pq 2  4  3 p 2 q  9 p 3  9 p 2
0
1 
 2
 3
 3 p  q 2  4 pq  3 p 2  3 p   3 p  q 2  4 pq  3 p( p  1)   3 p  q 2  4 pq  3 pq 
 3 p (q 2  pq )  3 p (q 2  (1  q )q )  3 p (q 2  q  q 2 )  3 pq
(das ist kein Beweis, der Beweis läuft über die vollständige Induktion)
--Allgemein: 2 = n p q

LAPLACE-Bedingung: wenn npq > 9 kann man Normalverteilung benutzen
Varianz npq > 9. Exakte Symmetrie bei p = q = 0,5.
Je symmetrischer und je größer n, desto besser die Approximation an die Normalverteilung.
Grenze bei npq = np(1-p) = 9 => nkritisch = 9 / ( 0,5 . 0,5 ) = 36.
Funktionsklasse fn (p) = n p (1-p) = n x (1 - x) = n (x – x2) Parabelschar
z.B. n = 36
f(x) = 36 (x – x2)
Thema 5
Verteilungen
Statistik - Neff
5.5 B INOMIALKOEFFIZIENTEN
n
Die Binomialkoeffizienten   kennen wir aus den Binomischen Formeln (a+b)n .
 x
Man entnimmt sie rekursiv aus dem PASCAL'schen Koeffizientenschema (siehe unten)
oder bestimmt sie mit einer der beiden folgenden Formeln:
 n  n  (n  1)  (n  2)  ...  (n  x  1)
n!

 
x!
x !(n  x)!
 x
n
Bei den meisten Taschenrechnern gibt es dazu die Taste [nCr]: Number of Combinations  
r 
(a+b)0 = 1
(a+b)1 = a + b
(a+b)2 = a2 + 2ab + b2
(a+b)3 = a3 + 3 a2b + 3 a b2 + b3
(a+b)4 =
=
=
=
=
=
1 a0b0
1 a1b0 + 1 a0b1
1 a2b0 + 2 a1b1 + 1 a0b2
1 a3b0 + 3 a2b1 + 3 a1b2 + 1 a0b3
1 a4b0 + 4 a3b1 + 6 a2b2 + 4 a1b3 + 1 a0b4
 4   4  4  4  4  4
     ;  ;  ;  ; 
 x   0  1   2   3   4 
2 2
6 a b bedeutet, dass die Kombination a2b2 bei (a+b)4 sechs mal vorkommt.
Binomialkoeffizienten:
 4  4  3  2 1kürzen
 6 (1.Formel)
 
 2  2 1  2 1kürzen
 4
4!
24

 6 (2. Formel).
 
 2  2! (4  2)! 2  2
mit Taschenrechner: 4[nCr]2
 75  75  74  73
 67525. 75! nicht mit Taschenrechner!
 
3  2 1
3 

Thema 5
5.6 Z IEHEN
Verteilungen
OHNE
Statistik - Neff
Z URÜCKLEGEN
Beispiel 5.3 (nach Lambacher-Schweizer S.135)
In einer Urne befinden sich M = 64 schwarze Kugeln und N  M = 36 weiße Kugeln.
"Treffer" sei das Ziehen einer schwarzen Kugel, d.h.
64
100  64
M
M
p
und q 
allgemein: p 
und q  1 
100
100
N
N
Es werden n = 5 Kugeln nacheinander gezogen. Stichprobenumfang n = 5.
Wie groß ist die Wahrscheinlichkeit unter den 5 Kugeln 3 schwarze zu ziehen, W(X=3) ?
Ziehen mit Zurücklegen BERNOULLI-Kette, p = 0,64 ist konstant, X ist binomialverteilt:
 5
64 64 64 36 36
W ( X  3)  f 5; 0,64 (3)     0,643  0,362  10 




 0,3397
100 100 100 100 100
 3
n  M  
M
allgemein: W ( X  x )  f n , p ( x )         1  
N
 x  N  
x
n x
(Binomialverteilung)
Ziehen ohne Zurücklegen: die Treffer-Wahrscheinlichkeit p ändert sich nach jedem Zug.
 5  64 63 62 36 35
W ( X  3)    
     0,3486
 3  100 99 98 97 96
 n  M M 1
N  M N  M 1
allgemein: W ( X  x)  f n , N , M ( x)     
 ...

 ...
N  x N  x 1
 x  N N 1
x fallende Faktoren n - x fallende Faktoren
M  N M 
 

x
nx 
Dieser Ausdruck lässt sich zusammenfassen zu W ( X  x)  f Hyp | n , N , M ( x)    
N
 
n 
Das ist die hypergeometrische Wahrscheinlichkeits-Funktion.
Wenn man die Symbole p und q aus der Binomialverteilung benutzt, ergeben sich
N n
1000  5
1
Erwartungswert µ = n p.
Varianz 2 = n p q 
.
1000  1
N 1
N n
N n
Standardabweichung σHyp  n  p  q 
=> Korrekturfaktor
N 1
N 1
  Die Funktionswerte fHyp | n | N | M (x) sind von 3 Parametern abhängig n, N, M.
Sie lassen sich deshalb schwer tabellieren.
n
 0, 05 kann man die Hypergeometrische Verteilung
N
mit Hilfe der Binomialverteilung approximieren (annähern).
Dies ist eine Approximationsbedingung.
Wenn der Auswahlsatz
Unter der weiteren Bedingung npq > 9 kann man sogar die Normalverteilung benutzen.
Wenn die Auswahlsatz-Bedingung n/N ≤ 0,05 verletzt ist, dann muss man den
N n
Korrekturfaktor
verwenden… siehe unten
N 1
Thema 5
Verteilungen
Statistik - Neff
5.7 H YPERGEOMETRISCHE V ERTEILUNG
Beispiel 5.4
Bei der Produktion von Elektromotoren seien im Durchschnitt 5% Ausschuss. p=0,05
Die Fertigungsmenge umfasst N=200 Stück.
Wie groß ist die Wahrscheinlichkeit dafür, dass bei einer Entnahme von n=20 Stück
a) genau 5 Stück Ausschuss b) alle verwendbar
c) höchstens 2 Stück Ausschuss sind?
d) Erwartungswert und erwartete Varianz und Standardabweichung?
e) Inwiefern ist es hier zulässig, die Binomialverteilung zu verwenden?
f) Aufgabenteil c) auch mit Binomialverteilung zum Vergleich.
1. Das ist eine Stichprobe ohne Zurücklegen, das ist der Normalfall!
2. N=200. n=20. n/N = 0,1 > 0,05 => fHyp. M = p·N= 0,05·200 = 10 Stück. nCr
10  190  10! 190!

 

5  15  5!5! 15!175! 252  6,58 1021

a) "genau 5" W ( X  5)  f 20;200;10 (5) 


 0, 001
200!
1, 611027
 200 


20!180!
 20 
10  190 
10!
190!

 

0
20  0!10! 20!170!
=0,3398
b) "0 Stück Ausschuss" W ( X  0)  f 20;200;10 (0)    

200!
 200 


20!180!
 20 
10  190  10  190 
 
   

1  19   2  18 

c) W ( X  0)  W ( X  1)  W ( X  2)  0,3398 


 200 
 200 




 20 
 20 
10! 190!
10! 190!


1!9! 19!171! 2!8! 18!172!
 0,3398 

 0,3398  0,3974  0,1975  0,9347
200!
200!
20!180!
20!180!
d) µ = n·p = 20·0,05 = 1 Stück Ausschuss
N n
200  20
 20  0, 05  0,95 
 0,95  0,9045  0,859 .
2 = n p q 
N 1
200  1
 = √0,859 = 0,927 Stück Ausschuss

e) Das ist nicht zulässig, weil für den Auswahlsatz gilt n/N = 0,1 > 0,05.
2
 20 
f) FBin | 20 | 0,05 (2)     0, 05x  0,9520 x 
x 0  x 
 20 
 20 
 20 
0
20
1
19
2
18
  0, 05  0,95    0, 05  0,95    0, 05  0,95 
0 
1 
2 
 0,3585  0,3774  0,1887  0,9245
Thema 5
Verteilungen
Statistik - Neff
5.8 N ÄHERUNG NACH P OISSON
Wenn Ereignisse selten auftreten, dann ist die Treffer-Wahrscheinlichkeit p klein.
Für kleine p kann man einen Grenzwert für n∞ bestimmen.
µ
µ
und q  1  p  1 
Für binomialverteilte Zufallsvariable gilt: µ  n  p  p 
n
n
x
n x
n
n  µ   µ 
f n; p ( x)    p x q n  x        1  
 x
 x  n   n 
 µ
 1  
 n
n x
n(n  1)(n  2)...(n  x  1) µ x  µ 

  1  
n  n  n  ...  n
x!  n 
n x
n(n  1)(n  2)...(n  x  1) µ x

 x
x!
n
n(n  1)(n  2)...(n  x  1) µ x  µ 

  1  
nx
x!  n 
µx n n 1 n  2
n  x 1  µ   µ 

 

 ... 
 1    1  
x! n n
n
n
 n  n
n
n x
x
x
µx  µ 
µx µ
 1  2   x  1   µ 
n 

 1   1 1  1   ... 1 

1



e
 

x!  n 
n   n
x!
 n  n  
n
2
1
x
 1   2   x 1   µ 
1 1   1   ... 1 
   1   streben alle für n  ∞ gegen den Grenzwert 1.
n   n
 n  n  
n
n
n
n


 µ
 1
 x
 x
2 lim 1    e µ  vgl. lim 1    e. lim 1    e x . lim 1    e x 
n 
n 
n 
n 
 n
 n
 n
 n


Die POISSON-Verteilung hat
µx  µ
µx
die Wahrscheinlichkeitsfunktion
f Poi| µ ( x) 
e 
x!
x ! eµ
µx  µ
FPoi | µ (k )    e
x 0 x !
µ = n·p
k
und die Verteilungsfunktion
der Erwartungswert ist
Tabelle 7.2
 µ  n
µ
weil σ 2  npq  µ  (1  p )  µ  1   
 n
nur einen Parameter, nämlich µ. Die Funktionswerte fPoi(x) lassen deshalb einfacher
berechnen und tabellieren als fBin(x) und fHyp(x).
[POISSON, Siméon Denis, Paris 1837]
erwartete Varianz
 = µ
Wenn die Approximationsbedingungen erfüllt sind, wird man die Hypergeometrische Verteilung
und die Binomialverteilung durch die POISSON-Verteilung approximieren:
Approximationsbedingungen:
n
M
M
 0, 05 mit p  .
µn
N
N
N
n
Übergang von fBin(x) zu fPoi(x) , wenn
 1500 (d.h. p klein, n groß)
p
n/N  0,05
n/p  1500
Hypergeom.Vert. 
 Binomial-Vert. 
 Poisson-Vert.
Übergang von fHyp(x) zu fBin(x) , wenn
Thema 5
Verteilungen
Statistik - Neff
5.9 P OISSON -V ERTEILUNG
Beispiel 5.5
In einem Unternehmen mit einer sehr großen Anzahl N sehr groß Telefonaten beträgt die
Anzahl der falschen Verbindungen p=1 % . Wie groß ist die Wahrscheinlichkeit, dass bei einer
Stichprobe von n=200 Telefonaten genau x=3 falsche Verbindungen entstehen?
1. Das ist eine Stichprobe ohne Zurücklegen.
"sehr große Anzahl der Telefonate" => n/N = 200/N < 0,05 => man kann fBin benutzen:
 200 
200  199  198
3
197
W ( X  3)  f Bin, 200; 0,01 (3)  
  0, 01  0,99  0,181
1 2  3
3 
2. Man kann sogar die POISSON-Verteilung benutzen, weil n/p = 200/0,01 = 20000 > 1500
µ = n p = 200·0,01 = 2 glatte Zahl => Tabelle
23
W ( X  3)  f Poi,2 (3) 
 0,1804 W(X=3)=W(X<3)-W(X<2)=0,8571-0,6767
3! e2
3. Wie groß muss N sein, damit man fBin benutzen darf? Grenze bei 200/N = 0,05 => N ≥4000.
4. Wie groß muss Stichprobenumfang n mindestens sein, damit man die POISSON-Verteilung
verwenden kann? Grenze bei n/0,01=1500 => n = 15.
Beispiel 5.6
In einem Betrieb werden viele, N groß Transistoren hergestellt, von denen im Durchschnitt 3%
fehlerhaft sind. Wie groß ist die Wahrscheinlichkeit, dass in einer Sendung von n=100 Stück
Treffer e fehlerhaft,
e) Mit welcher Verteilung kann man hier die Wahrscheinlichkeiten bestimmen?
Prüfen Sie die Approximationsmöglichkeiten genau.
a) keine Ausschuss-Stücke x=0, b) genau 5 Ausschuss-Stücke,
c) höchstens 4 Ausschuss-Stücke,
d) mindestens 8 Ausschuss-Stücke enthalten sind?
e) Das ist eine Stichprobe ohne Zurücklegen. N ist sehr groß,
(1) wegen n/N <0,05 kann man fBin verwenden.
(2) p klein?"Ausschuss" ist ein seltenes Ereignis: wegen 100/0,03=3333 > 1500
=> kann man fPoi verwenden.
µ = 100·0,03 = 3, für diesen Erwartungswert liegt eine Tabelle vor => Tabelle 7.2
30
a) W ( X  0)  f 3 (0)  F3 (0)  e 3  0, 0498  5%
0!
x
x
5
4
3
3
b) W ( X  5)   e 3   e 3  F3 (5)  F3 (4)  0,9161  0,8153  0,1008  10%
x 0 x !
x 0 x !
3x 3
e  F3 (4)  0,8153
x 0 x !
d) W ( X  8)  1  F3 (7)  1  0,9881  0, 0119
4
c) W ( X  4)  
Thema 5
Verteilungen
Statistik - Neff
5.10 D ISKRETE V ERTEILUNGEN
Aufgabe Diskrete Verteilungen
gegeben:
Sachverhalt wie in den obigen Beispielen,
(versteckte) Hinweise auf "Ziehen ohne Zurücklegen", "große N",
Tabellen und Approximationsbedingungen in der Formelsammlung.
gesucht / Schritte:
1. Passendes Modell aufgrund der Approximationsbedingungen
entscheiden, ob fHyp , fBin , fPoi hier benutzt werden können/sollen/müssen,
dazu die Liste der Approximationsbedingungen als Checklist einsetzen.
2. Wahrscheinlichkeiten für einzelne Ereignisse oder Intervalle
aus der Binomial-, hypergeometrischen oder/und POISSON-Verteilung.
Vergleich zu Ergebnissen mit anderen Verteilungen.
Formelmäßige Ansätze für die konkret gegebenen Zahlen.
Prüfen, ob eine geeignete Tabelle vorhanden ist,
Wahrscheinlichkeiten durch Rechnen anhand der Formeln oder mit Hilfe
der Tabelle bestimmen,
W(X ist "mindestens" k) = 1 – W(X ist "höchstens" k–1)
Vergleichsrechnung mit anderer Wahrscheinlichkeitsverteilung durchführen (über Tabelle oder Berechnen der betreffenden Werte).
Ansätze, indem man die konkreten Zahlen in die Formeln einsetzt.
3. Erwartungswert, erwartete Varianz, erwartete Standardabweichung
p, q, n, evtl. N in die entsprechenden Formeln einsetzen
Thema 5
Verteilungen
Statistik - Neff
5.11 N ORMALVERTEILUNG
Die meisten Merkmale X lassen sich mit Hilfe der Normalverteilung untersuchen.
Das gilt besonders für Zufallsvariable X, die durch Überlagerung vieler Zufallsvariablen entstehen.
Für normalverteilte Zufallsvariable gilt
die Dichtefunktion
1  xµ 

σ 
2
 
1
f Norm|μ,σ ( x) 
e 2
σ 2
x
1  xµ 
2
2
 

1
die Verteilungsfunktion W ( X  x2 )  FNorm|μ,σ ( x2 ) 
e 2  σ  dx

σ 2 
[DE MOIVRE, Abraham, 1733 London, GAUSS, Carl Friedrich, 1826 Göttingen]
 Excel / Normalverteilung
Dichtefunktion fNorm | 4 | 1,55
Verteilungsfunktion FNorm | 4 | 1,55
Eigenschaften der Dichtefunktion fNorm | µ | 
1. Zwei Parameter Erwartungswert µ, Standardabweichung 
2. Die Dichten fµ,(x) sind symmetrisch zur Achse x = µ.
3. Der Hochpunkt liegt bei (µ | f(µ)), das typische zentrale Maximum
4. Die Wendepunkte bei x1;2 = µ  .
5. Die Dichten fµ,(x) konvergieren für x   ∞ gegen null.
6. Mit zunehmender "Streuung"  wird der Funktionsgraph breiter und flacher.
7. Die Verteilungsfunktion FNorm | µ | ist S-förmig, monoton steigend, lim F ( x)  1 .
x 
Die Dichtefunktion der standardisierten Normalverteilung fSN(z) =
1  x 0 
1
 z2
1  12 z 2
e
 0, 4e 2
2
2
 

1
1  12 x2
f SN |0|1 ( x) 
e 2 1  
e
erhält man mit µ = 0 und  = 1
1 2
2
Die Dichten sind symmetrisch zur f(z)-Achse, Hochpunkt (0 | 0,4), Wendepunkte (1 | ±0,24).
z
1 2  12 z2
Tabelle 7.6
e dz
2 
sie ist parameterfrei, eine einzige Funktion, eine einzige Tabelle!
xµ
z
bzw. x  µ  z  
Mit den Umrechnungen

schließt man von konkreten x-Werten auf standardisierte z-Werte und umgekehrt.
Oft schreibt man auch z statt fSN(z) und (z) statt FSN(z).
Die Verteilungsfunktion W ( Z  z2 )  FSN ( z2 ) 
Thema 5
Verteilungen
Statistik - Neff
5.12 "24-S TUNDEN -L ICHTER "
Beispiel 5.7
Die Brenndauer handelsüblicher Kerzen von Typ "24-Stunden-Licht" ist näherungsweise
normalverteilt mit einem Erwartungswert µ = 24 Stunden und einer Standardabweichung von
 = 4 Stunden. Stetige Zufallsvariable!
Standardisierung:
µ = 24
 = 4
x  µ x  24


4
x=µ+z.¾
z
Achse z
x-Achse: Brenndauer x [Stunden]
konkrete Achse
Wie groß ist die Wahrscheinlichkeit dafür, dass eine solche Kerze
a) höchstens 30 Stunden brennt?
b) höchstens 16 Stunden brennt?
c) mehr als 16 Stunden brennt? (Gegenwahrscheinlichkeit von b)
d) mindestens 20 Stunden brennt? Stetige Zufallsvariable!
e) zwischen 24 – 1 und 24 + 1 Stunden brennt, also im 1--Bereich liegt ?
f) zwischen 20 und 26 Stunden brennt?
g) zwischen 24–1,96  und 24+1,96  Stunden brennt? (d.h. im 95%-Bereich liegt?)
[24-7,84 ; 24 + 7,84] = [16,16 h ; 31,84 h]
h) Wir messen die Brenndauer bei 25 Kerzen, Erwartungswert und
erwartete Standardabweichung des Stichprobenmittels X sind zu berechnen.
30  24
 1,5  W ( X  30)  FSN (1,5)  0,9332
FSN ( z )  Spalte!
4
16  24
b) z 
 2  W ( X  16)  FSN (2)  0, 0228
FSN (  z )  Spalte
4
c) Gegenwahrscheinlichkeit in der Gegenspalte: 1  FSN (2)  FSN (2)  0,9772
a) z 
20  24
 1  W ( X  20)  1  W ( X  20)  1  FSN (1)  1  0,1587  0,8413
4
e) 1  Intervall: D(1)  0, 6827  W (20  X  28)  FSN (1)  FSN (1)  0,8413  0,1587
d) z 
f) µ  4  X  µ  2 nicht symmetrisch, nicht mit D(z) z1 
W (20  X  26)  W ( X  26)  W ( X  20) 
 FSN (0,5)  FSN (1)  0, 6915  0,1587  0,5328
g) 1,96  Intervall: D(1,96)  0,9500
h) µX  µx  24 [Stunden]
σX 
σ
4
  0,8 [Stunden]
n 5
20  24
26  24
 1. z2 
 0,5
4
4
Thema 5
5.13 T ABELLE
Verteilungen
Statistik - Neff
ABLESEN
Ablesebeispiele
FSN(-z) = W(X  16)
FSN(+z) = W(X  30)
D(z) = W(18  X  30 )
Verteilungsfunktion der standardisierten Normalverteilung FSN(z) =
1
2
z2
e
1
 z2
2
dz

a) für z > 0 als Tabelle FSN(z)
tabelliert,
z.B. FSN(1,7) = 0,9554
b) FSN(z) konvergiert für z  
nach 1 = 100%.
c) Wendepunkt bei W(0 | 0,5)
Thema 5
Verteilungen
Statistik - Neff
5.14 S TETIGKEITSKORREKTUR
Für einigermaßen normalverteilte stetige Zufallsvariablen benutzt man die Normalverteilung.
Unter bestimmten Approximationsbedingungen geht das auch für diskrete Zufallsvariable.
Beispiel 5.2 noch einmal
An einem erosionsgefährdeten Hang sollen 10 Fichtenpflanzen angepflanzt werden.
Die Baumschule gibt eine Anwachswahrscheinlichkeit von p = 40% an.
Wie groß ist die Wahrscheinlichkeit, dass höchstens 5 anwachsen?
Man kann die Mittelpunkte der Rechteckoberkanten im Histogramm zur Binomialverteilung verbinden. Diese "Hüllkurve" ist
eine Approximation der Dichtefunktion der
Normalverteilung.
Ganz entsprechend gilt das für die
Verteilungsfunktionen FBin(k) und
FNorm(x)
 10  k 10k
0, 4 0,6
k 0 

5
FBin | 10 | 0,4 (5) = 0,8338
=
 k
µ = 10.0,4 = 4
¾ = √npq
54
 0, 645 . FSN(0,645) = 0,7406
1,55
x  0,5  µ 5  0,5  4 5,5  4
mit Stetigkeitskorrektur: z 


 0,967 FSN(0,967) = 0,8334
σ
1,55
1,55
Wenn man diskrete Zufallsvariable mit der Normalverteilung untersucht, verbessert
die Stetigkeitskorrektur den Näherungswert.
x  0,5  µ
Standardnormalvariable z mit Stetigkeitskorrektur: z 
σ
weiter Beispiel 5.2
Eigentlich darf man für eine binomialverteilte Zufallsvariable nur dann die Normalverteilung
als Näherung benutzen, wenn gilt Varianz 2 = npq > 9.  > 3. LAPLACE-Bedingung.
Hier ist 2 = 10·0,4·0,6 = 2,4 < 9.
Mit der Stetigkeitskorrektur ist trotzdem eine recht gute Näherung erreicht worden!
□ Nun sollen an dieser Stelle 40 Fichtenpflanzen angepflanzt werden.
Wie groß ist die Wahrscheinlichkeit, dass höchstens 20 Pflanzen anwachsen?
 2 = n p q = 40 · 0,4 · 0,6 = 9,6 > 9 approximierbar
µ = 10 · 0,4 = 4. 2 = 10 · 0,4 · 0,6 = 2,4.  = 1,55. z 
Thema 5
Verteilungen
Statistik - Neff
 20  0,5 16 
W(X  20) =FSN(z) = FSN 
  FSN (1, 45)  0,9265 zum Vergleich: FBin(20) = 0,926
3, 098


5.15 AUFGABEN
ZUR
N ORMALVERTEILUNG
Aufgabe Normalverteilung
gegeben:
Sachverhalt mit diskreter (binomialverteilter) oder stetiger Zufallsvariablen.
Tabellen und Approximationsbedingungen in der Formelsammlung.
gesucht / Schritte:
1. Approximationsbedingungen für die Normalverteilung prüfen
stetige Zufallsvariable: ohne weiteres anwenden
diskrete Zufallsvariable:
n/N  0,05
n/p  1500
Hypergeom.Vert. 
 Binomial-Vert. 
 Poisson-Vert.
npq>9
Binomial.Vert 

 Normalverteilung
dann mit Stetigkeitskorrektur rechnen
2. Wahrscheinlichkeiten für bestimmte Intervalle
Formelmäßige Ansätze für die konkret gegebenen Zahlen.
jeweils benötigte Standard-Normalvariable z brechnen aus:
xµ
x  0,5  µ
z
stetig bzw. z 
diskret berechnen,
σ
σ
damit FSN(z) oder DSN(z) berechnen,
wie in den Beispielen 5.7 und 5.2 (Abschnitt 5.14)
W(X ist "mindestens" k) = 1 – W(X ist "höchstens" k)
3. µ, 2,  für das Stichprobenmittel
σ
µX  µx , σ X 
anwenden
n
4. Eigenschaften der Normalverteilung und der Standard-Normalverteilung
in Zusatzfragen
überlegt man sich am leichtesten, indem man sich die Funktionsgraphen
zu den Dichtefunktionen fNorm | µ |  (x) bzw. fSN(z) vorstellt oder skizziert.
Thema 5
Verteilungen
Statistik - Neff
5.16 APPROXIMATIONSBEDINGUNGEN
Übergang von der
wenn n/N ≤ 0,05
wenn n/p ≥ 1500
wenn n/N ≤ 0,05 und n/p ≥ 1500
Hypergeometrischen V.
Binomial-V.
Hypergeometrischen V.
zur Binomial-V.,
zur POISSON-V.,
zur POISSON-V.,
Binomial-V
Hypergeometrischen V.
POISSON-V.
STUDENT-t-V.
zur Normalverteilung, wenn 2 = n p q > 9 (LAPLACE-Bedingung)
zur Normalverteilung, wenn n/N ≤ 0,05 und 2 = n p q > 9
zur Normalverteilung, wenn µ = 2 > 9
zur Normalverteilung,
wenn n > 30, bei normalverteilter Grundgesamtheit
wenn n > 50, bei unbekannter Verteilung der Grundgesamtheit
 Excel / Normalverteilung / Zeile 117
Anpassung und Korrekturfaktoren
Diskrete Zufallsvariable X
x  0,5  µ
(Stetigkeitskorrektur)
σ
σ
x µ
σx 
 z
n
σ
n
z
Stichprobenmittel σ X
n/N > 0,05:
korrigiert = ·
N n
N 1
xµ
x µ
bzw. t 
n
s
s
 wird durch die Standardabweichung s aus der Stichprobe ersetzt
  unbekannt, n < 30 bzw. n < 50
Binomial
Hypergeometrisch
Poisson
unter den
Approximationsbedingungen:
n/N ≤ 0,05
2 = n p q > 9
t
StandardNormalverteilung
fSN(z), FSN(z)
(Thema 6)
4 Anpassungsprobleme
1. Umrechnung
konkret – standardisiert
x µ
z

2. Für Stichprobenmittelwerte
x statt Einzelobjekte x
x µ
z
 n

3. Für ohne Zurücklegen bei
n/N > 0,05
x µ
z
 n
Nn

N 1
4.  unbekannt, ersatzweise
s aus der Stichprobe nutzen:
x µ
t
 n
s
Thema 5
5.17
Verteilungen
CHI 2 -,
Statistik - Neff
S TUDENT - T -, F ISHER -F- V ERTEILUNG
a) Chi2-, 2-Verteilung
[Pearson, Karl, chi2 , London, ca. 1914]
Eine stetige Zufallsvariable X ist 2-verteilt mit Freiheitsgraden, wenn ihre Dichtefunktion
f ν ( ) 
1
2
ν
ν
1
2 2
 ( )
e

2
2
2 2  ( 12 ν)

mit ( x)   e t  t x 1dt (Gammafunktion)
0
 Tabelle 7.4
Es seien X1, X2, … , X  unabhängige standardnormalverteilte Zufallsvariable.
Dann ist die Zufallsvariable C  X 12  X 22  ...  X ν2 2-verteilt.
Anwendungen:
(1) Chi2-Unabhängigkeitstest, zum Prüfen nominaler Merkmale auf Unabhängigkeit (4.4)
(2) Chi2-Anpassungstest, zum Prüfen, ob eine Zufallsvariable normalverteilt ist (5.17)
(3) Varianztest, zum Testen, ob s2Stichprobe signifikant von 2Grundgesamtheit abweicht.
b) t-Verteilung (STUDENT-t-Verteilung)
[GOSSET, WILLIAM, "STUDENT", Dublin, Irland, 1908]
Eine stetige Zufallsvariable X ist t-verteilt mit Freiheitsgraden, wenn ihre Dichtefunktion
 ν 1 
ν 1

  t 2  2
 2   1
f (t ) 


ν
 ν    2ν  

mit ( x)   et  t x 1dt
(Gammafunktion)
0
 Tabelle 7.5
Es sei X eine standardnormalverteilte Zufallsvariable und C eine 2-verteilte Zufallsvariable
mit  Freiheitsgraden. X und C sind unabhängige Zufallsvariable.
X
Dann ist die Zufallsvariable T 
student-t-verteilt mit  Freiheitsgraden.
C
ν
Anwendungen:
(1) Multiple Regressionsanalyse, zum Prüfen, ob ein Einflussfaktor einen signifikanten
Beitrag zur Regression liefert. (Abschnitt 1.14)
(2) Hypothesentests, zum Prüfen, ob xStichprobe signifikant von µGrundgesamtheit abweicht,
anstelle der Normalverteilung, wenn Grundgesamtheit unbekannt ist. (Abschnitt 6.3)
c) FISHER -F-Verteilung
[FISHER, RONALD, Rothamsted, GB, 1918]
Die Zufallsvariable X sei 2-verteilt mit p Freiheitsgraden und die von X unabhängige Zufallsvariable Y sei2-verteilt mit  Freiheitsgraden, dann ist die Zufallsvariable Z
1
X
p
Z
FISHER-F-verteilt mit den Freiheitsgraden p und 
1
Y
ν
  Tabelle 7.3
Anwendungen:
(1) Korrelationsanalyse, zum Prüfen, ab ein signifikanter Zusammenhang besteht (1.11).
(2) Varianzanalysen, z.B. zum Testen, ob s2Stichprobe A signifikant von s2Stichprobe B abweicht.
Thema 5
5.18 I ST X
Verteilungen
NORMALVERTEILT
Statistik - Neff
?
Schon oft hieß es "normalverteilte" Zufallsvariable.
Es ist zu prüfen, ob eine Zufallsvariable "einigermaßen" normalverteilt ist.
Wir werten eine möglichst große Stichprobe aus => k Klassen, Häufigkeiten ni, x, s.
Wir vergleichen diese beobachteten Häufigkeiten ni mit den theoretischen Häufigkeiten ui.
Genau so sind wir beim Chi2-Unabhängigkeitstest vorgegangen (Abschnitt 4.4).
Als Testgröße bilden wir wieder die Summe der normierten Abweichungsquadrate
2
empirisch
chi

2
empirisch
k
 ni  ui 
i 1
ui

2
und testen mit dem Prüfmaß 2crit.
Der Test heißt Chi2-Anpassungstest, weil die Güte der Anpassung einer theoretischen Verteilung
an eine empirische Verteilung überprüft wird.
Die Nullhypothese H0 lautet: die zu prüfende Grundgesamtheit gehorcht der Normalverteilung.
Wir sprechen besser von Verteilungshypothese, die zu bestätigen oder abzulehnen ist.
Auf ähnliche Weise kann man prüfen, ob eine Zufallsvariable einer anderen theoretischen Verteilung gehorcht,
etwa ob sie POISSON-verteilt ist, oder ob sie jene Dichtefunktion für die Verspätung X der U-Bahn hat…
Beispiel 5.8 (nach Bleymüller S.129)
Es soll geprüft werden, ob die "Lebensdauer" X eines bestimmten Akku-Typs normalverteilt ist.
Es wurde eine Stichprobe im Umfang n = 80 Stück ausgewertet. Signifikanzniveau  = 0,05.
Die stetige Zufallsvariable Lebensdauer wurde in 7 Merkmalsklassen gegliedert: k = 7.
Als mittlere Lebensdauer ergibt sich x = 3,41[Jahre], die Standardabweichung ist s = 0,7 [Jahre].
1. Zunächst eine Arbeitstabelle mit der Häufigkeitsverteilung der k Klassen [xiunten ; xioben].
x und s sind schon gegeben, die Klassenmitten xi* und die Spalte xi2·ni benötigen wir nicht.
 Excel / Anpassungstest
2. Wir benötigen die Wahrscheinlichkeiten FSN(zi) für die Intervalle –∞ < X ≤ xioben.
x oben  x
Dazu bestimmen wir die Standardnormalvariablen zi  i
.
s
Für diese zi lesen wir aus der Tabelle FSN die Werte FSN(zi) ab.
3. Wir benötigen die Wahrscheinlichkeiten (= theoretische relative Häufigkeiten) wi für
die Klassen i. Wir erhalten die wi durch Differenzenbildung wi = FSN(zi) – FSN(zi – 1) .
Dabei setzen wir FSN(z0) = 0.
4. Wir benötigen die theoretischen absoluten Häufigkeiten ui = n · wi. <= wi = ui / n
Beim Chi2-Anpassungstest wird vorausgesetzt, dass in jeder Klasse ui ≥ 5 ist.
Wenn dies nicht der Fall ist, dann müssen Klassen entsprechend zusammengefasst werden.
5. Zum Vergleichen der empirischen Häufigkeiten ni mit den theoretischen Häufigkeiten ui
bildet man die Summe der normierten Abweichungsquadrate 
2
empirisch
k
 ni  ui 
i 1
ui

2
6. Zum Ablesen des Prüfmaßes  crit benötigen wir den Sicherheitsgrad 1 – 
und die Freiheitsgrade:  = k – p – 1.
k ist die Anzahl der Klassen, p ist die Anzahl der Parameter (x, s) , die aus der Stichprobe
ermittelt wurden. Wenn µGrundgesamtheit gegeben ist, dann ist k = 1.
2
2
2
7. Die Verteilungshypothese bestätigen wir, wenn empirisch
(H0 wir beibehalten).
 crit.
Thema 5
Verteilungen
Statistik - Neff
5.19 C HI 2 - ANPASSUNGSTEST
Aufgabe Anpassungstest
gegeben:
Häufigkeitsverteilung mit k Klassen und den Häufigkeiten ni .
x , s aus der Stichprobe oder µ, aus der Grundgesamtheit.
Verteilungshypothese. Signifikanzsniveau (Irrtums-Wahrscheinlichkeit) .
gesucht:
Es ist zu prüfen, ob die untersuchte Zufallsvariable normalverteilt ist.
Arbeitstabelle und Zwischenschritte sind anzugeben.
Schritte:
Wie auf der vorangehenden Seite dargestellt.
a) Arbeitstabelle mit Spalte xioben
xioben  x
s
b) Spalte Standardnormalvariablen zi 
c) Spalte
d) Spalte
e) Spalte
f) Spalte
FSN(zi)
wi = FSN(zi) – FSN(zi – 1)
ui = n · wi Klassen zusammenfassen, wenn ui ≥ 5
 ni  ui 
g) Summe bilden: 
2
ui
k
2
empirisch

 ni  ui 
2
ui
h) Freiheitsgrade berechnen  = k – p – 1.
p ist 0, 1 oder 2 je nachdem wie viele Parameter aus der Stichprobe kommen.
i 1

i) 2crit in Tabelle 7.4 ablesen: 2crit | 1 –  | . (bei Sicherheitsgrad 1 – )
2
2
j) Verteilungshypothese bestätigen, wenn empirisch
, andernfalls ablehnen
 crit.
