Komplexe Zahlen

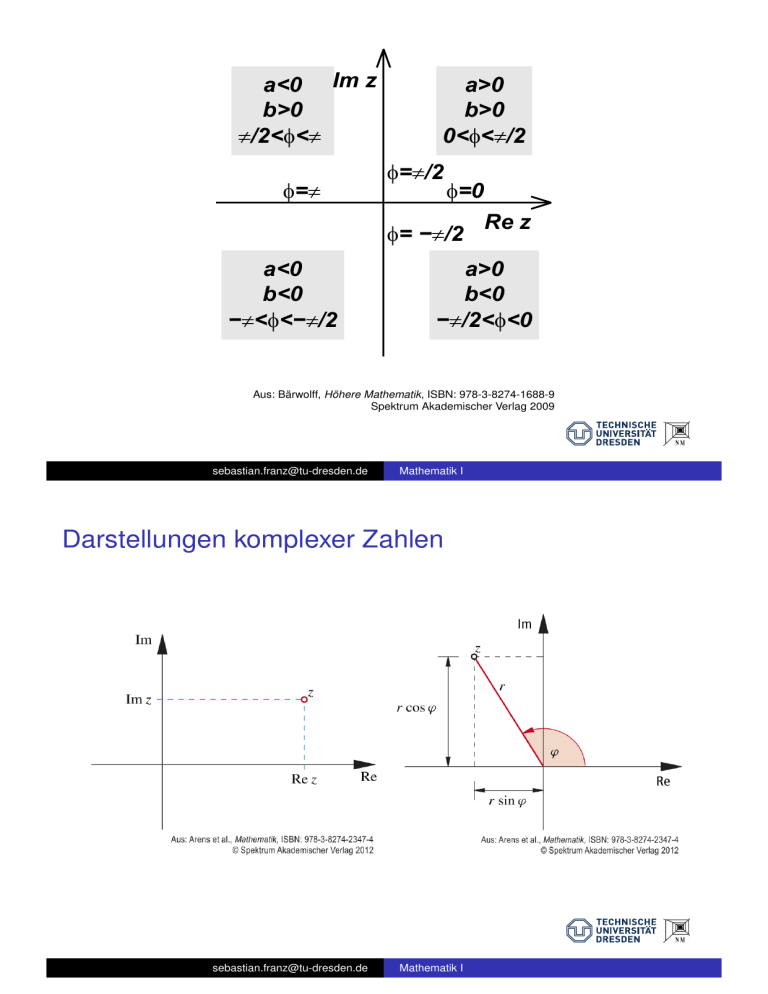
a<0 Im z
b>0
π/2<φ<π
φ=π
a<0
b<0
−π<φ<−π/2
a>0
b>0
0<φ<π/2
φ=π/2
φ=0
Re z
φ= −π/2
a>0
b<0
−π/2<φ<0
Aus: Bärwolff, Höhere Mathematik, ISBN: 978-3-8274-1688-9
Spektrum Akademischer Verlag 2009
[email protected]
Mathematik I
Darstellungen komplexer Zahlen
[email protected]
Mathematik I
Elementare Funktionen in Komplexen Variablen
Definition
Eine Funktion
p(z) = an z n + an−1 z n−1 + . . . + a1 z + a0
mit den Koeffizienten a0 , . . . an ∈ C und an 6= 0 heißt Polynom
über C vom Grad n.
Satz (Fundamentalsatz der Algebra)
Jedes Polynom p(z) vom Grad n ≥ 1 besitzt in C eine Nullstelle.
[email protected]
Mathematik I
Elementare Funktionen in Komplexen Variablen
Folgerung
Jedes Polynom pn (z) vom Grad n ≥ 1 besitzt in C genau n
Nullstellen, welche nicht paarweise verschieden sein müssen.
Jedes Polynom pn (z) in C vom Grad n ≥ 1 läßt sich in n
Linearfaktoren zerlegen,
n
pn (z) = an
∏ (z − zk ),
k=1
wobei die zk ∈ C die Nullstellen von pn (z) sind.
Bemerkung
Sind alle Koeffizienten reell und z0 eine nichtreelle Nullstelle
des Polynoms, so ist z0 ebenfalls eine Nullstelle.
[email protected]
Mathematik I
Elementare Funktionen in Komplexen Variablen
Definition
Die komplexe Exponentialfunktion für z = x + iy mit x, y ∈ R
lautet
ez := ex+iy = ex eiy = ex [cos y + i sin y ].
Sie ist periodisch in y .
Definition
Der Hauptwert der komplexen Logarithmusfunktion als
Umkehrfunktions zu ez lautet
ln z := ln |z| + iarg(z),
wobei arg(z) ∈ (−π, π].
[email protected]
Mathematik I
Elementare Funktionen in Komplexen Variablen
Definition (trigonometrische Funktionen für z ∈ C)
1
cos(z) := (eiz + e−iz ),
2
sin(z) :=
1 iz
(e − e−iz )
2i
Definition (hyperbolische Funktionen für z ∈ C)
1
cosh(z) := (ez + e−z ),
2
1
sinh(z) := (ez − e−z )
2
Zusammenhang für z = x + iy
cos(z) = cosh(iz)
= cos(x) cosh(y) − i sin(x) sinh(y)
sin(z) = −i sinh(iz)
= sin(x) cosh(y) − i cos(x) sinh(y)
[email protected]
Mathematik I
Zusammenfassung Kapitel 1 – Komplexe Zahlen
Zahlenbereiche N ⊂ Z ⊂ Q ⊂ R ⊂ C
i2 := −1
z = x + iyp= r (cos(ϕ) + i sin(ϕ)) = reiϕ mit
r = |z| = x 2 + y 2 und ϕ = arg(z) ∈ (−π, π]
Rechnen in C:
addieren/subtrahieren einfacher in algebraischer Form
multiplizieren/dividieren einfacher in trigonometrischer oder
exponentieller Form
In C hat jede Zahl genau n Stück n-te Wurzeln.
Jedes Polynom n-ten Grades hat in C genau n Nullstellen.
[email protected]
Mathematik I