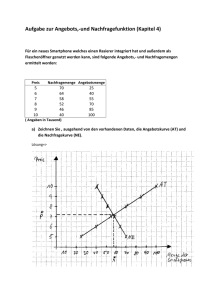
Nachfragefunktion

Tutorium Volkswirtschaftslehre theoretische Lösungen
1. Was versteht man unter abnehmenden Grenznutzen:
Güter stiften für den Konsumenten Nutzen, z.B. löscht ein Glas Wasser den
Durst. Der Grenznutzen bezeichnet den zusätzlichen Nutzen den eine weitere
Einheit eines Gutes dem Konsumenten stiftet (2. Glas Wasser, 3. …).
Das 1. Gossen´sche Gesetz besagt, dass der Grenznutzen jeder weiteren
konsumierten Einheit immer kleiner wird. Sättigung tritt ein, wenn der
Grenznutzen Null wird. Sättigungsgesetz
Skript Folie 31
2. Worin sehen Sie den Unterschied zwischen der kardinalen und der
ordinalen Nutzenlehre
Die kardinale Nutzenlehre geht davon aus, dass der Nutzen eins Gutes sich
genau Messbar in Nutzeneinheiten darstellen lässt, wie beispielsweise das
Gewicht.
Beispiel:
Gut A:
Gut B:
Gut C:
Gut D:
12 Nutzeneinheiten (NE)
18 NE
24 NE
27 NE
 Der Konsument würde dann im Vergleich zum Gut B das Gut A = 0,67, das
Gut C 1,34 und das Gut D = 1,5 mal „lieber“ haben (präferieren)
z.B. Gut A/Gut B = 12/18 = 0,67
Gut C/Gut B= 24/18= 1,34
Die ordinale Nutzenlehre geht von einem 2. Güter Fall aus und unterscheidet
den Nutzen in: (gut, besser, gleich gut). So wird eine Rangfolge gebildet, man
geht aber von keinen genauen Zahlen aus. U = f(x1, x2)
Beispiel: x1= Obst
x2= Gemüse
Konsument A präferiert Obst, deshalb stiftet ihm eine Mengeneinheit Obst einen
höheren Nutzen als Gemüse. UG<UO
Konsument B bevorzugt Gemüse, deshalb ist für den Nutzen durch eine
Mengeneinheit Obst höher. UO<UG
3. Was versteht man unter einer Indifferenzkurve?
(verbale und grafische Darstellung)
Eine Indifferenzkurve beschreibt Mengenkombinationen(Punkte der Höhenlinie
zwischen zwei Gütern), die den Haushalten gleichen Nutzen stiften.
(Kurven gleichen Nutzens).
So könnte es z. B. einem durstigen Konsumenten egal sein, ob er seinen
Durst mit 2 Gläsern Mineralwasser, mit 2 Gläsern Limonade oder mit 1 Glas
Mineralwasser und 1 Glas Limonade löscht.
Der Nutzen wird dabei im dreidimensionalen Raum dargestellt.
Auf einer Indifferenzkurve besteht für jede Güterkombination immer das gleiche
Nutzenniveau. Siehe Skript Folie 35,36
4. Stellen sie in einem Mengendiagramm (X1,X2) mögliche
Indifferenzkurven für Brillengestelle und Brillengläser sowie für Obst und
Gemüse dar.
Brillen und Brillengläser sind perfekte Komplemente, das heißt wer ein
Brillenglas nachfragt wird auch fast immer ein Brillengestell nachfragen.
Bei Obst und Gemüse können die Indifferenzkurven verschiedene Formen
annehmen. Bei neutralen Gütern bevorzugt der Konsument ein Gut vollständig
und fragt ausschließlich dieses Gut nach. Der Nutzen dieses Gutes wird durch
das andere Gut nicht ersetzt. Dementsprechend verläuft die Indifferenzkurve
abhängig vom bevorzugten Gut entweder vertikal oder horizontal.
Beispiel: Konsument mag nur Obst und kein Gemüse, Konsument mag nur
Gemüse kein Obst.
Bevorzugt ein Konsument ein Gut, konsumiert aber auch ein anderes Gut, dann
verschiebt sich die Indifferenzkurve in Richtung des bevorzugten Gutes.
5. Ein Haushalt verfügt über ein wöchentlich zu verausgabendes
Einkommen von 400 €. Der Haushalt fragt zwei Güter X1 und X2 nach,
deren Preise P1 = 20 € und P2 = 10 € betragen.
a) Welche Menge der beiden Güter könnte der Haushalt kaufen, wenn er
jeweils nur eins der Güter nachfragt?
Y/P1= 400/20€= 20 ME von X1
Y/P2= 400/10€= 40 ME von X2
b) Wie lautet die Funktionsgleichung der Budgetgeraden des Haushalts
allgemein und speziell?
Y=C= p1*x1 + p2*x2
- p1 • x1 = P2 • x2 - Y
x1 = - (p2/ p1) X1 + Y/p1 allgemeine Funktionsgleichung
400= 20*x1 + 10*x2
- 20 • x1 = 10 • x2 - 400
x1 = - ½ • x2 + 20
spezielle Funktionsgleichung
d) Was ändert sich, wenn sich der Haushalt entschließt, 20% seines
Einkommens zu sparen? Zeichnen Sie die neue Budgetgerade!
Parallelverschiebung der Budgetgeraden nach links unten bei sinkendem
Einkommen.
e) Wie wirkt sich eine Änderung der relativen Preise der beiden Güter auf
die Lage der Budget/Bilanzgeraden aus?
Bei einer relativen Preisänderung verändert sich die Steigung der Budgetgeraden
zwischen den beiden Gütern.
6. Wie erhält man eine Engelkurve?
Die Engelkurve zeigt wie sich die mengenmäßige Nachfrage eines Haushaltes
nach verschiedenen Gütern, mit steigendem Einkommen verändert.
Die Nachfrage nach einem teureren Gut (z.B. Kaviar) nimmt stark zu, während
die Nachfrage nach dem billigeren Gut (Brot) immer schwächer ansteigt.
Dadurch verändern verschieben sich die Tangierungspunkte der
Indifferenzkurven mit der Budgetgeraden. Verbindet man die verschiedenen
Tangierungspunkte dann erhält man die Engelskurve
(Einkommens- und Konsumkurve).
Siehe Grafik Folie 52
7. Wie verläuft normalerweise die Nachfragefunktion in einem PreisMengendiagramm?
Die Nachfragefunktion verläuft in einem Preis- Mengendiagramm
normalerweise von links oben nach rechts unten. Bei sinkendem Preis steigt die
Nachfrage nach einem Gut und umgekehrt.
Siehe Grafik Folie 59
8. Nennen Sie Beispiele, wo die Nachfragefunktion einen atypischen
Verlauf aufweist?
Ein Beispiel für einen atypischen Verlauf sind Luxusgüter. Die Nachfrage nach
einem Luxusgut (Porsche, Jacht) steigt nicht unmittelbar bei fallenden Preisen,
da der Preis hier als Statussymbol wirkt. Man spricht dabei vom Snobeffekt.
Bei nicht substituierbaren, lebensnotwendigen Gütern (Wasser) wird auch bei
steigen Preisen nicht weniger nachgefragt. Genauso wird bei fallenden Preisen
nur begrenzt mehr nachgefragt. Die Nachfragekurve hat dabei nur eine sehr
geringe Steigung.
II. Angebotstheorie
1.
Ein Sonnenbrillenunternehmer produziert seine Brillen nach einer linearen
Kostenfunktion und bietet in einem Polypolmarkt unter vollständiger Konkurrenz an.
a) Zeichnen Sie seine Kosten- und Erlösfunktion unter der Annahme ein, dass
der Unternehmer mit Gewinn arbeitet. Beschriften sie alle wichtigen
Informationen und erläutern Sie diese.
b) Wie sieht die Situation des Unternehmers bei einer
Grenzgrößenbetrachtung aus?
c) Die Konkurrenz auf dem Sonnenbrillenmarkt ist im Sommer 2007 so hoch
und der Preis sinkt so stark, dass der Unternehmer gerade noch als
Grenzanbieter auftreten kann. Zeichnen Sie seine neue Situation sowohl in
Gesamtgrößenbetrachtung als auch unter Grenzgrößenbetrachtung.
a) Lineare Kostenfunktion
Gewinnmaximum bei Gesamtgrößenbetrachtung
A....... Nutzenschwelle
xmax... gewinnmaximale Produktionsmenge; Der Preis P ist ein Datum für den
Mengenanpasserb) Gewinnmaximum bei Grenzgrößenbetrachtung
Kapazitätsgrenze
TDK
p = E´
GK = VDK
TDK
Gesamtgewinn
A
p = E´
1
1
p
2
GK (=VDK)
p
3
x
X1
X max
c)
Gesamtgrößenbetrachtung
E = P neu * X
P
K aX + b
b
XMax
Sonnenbrillen
Grenzgrößenbetrachtung:
P
TDK
P = konst.
XMax
Sonnenbrillen
3) c) Bietet das Unternehmen als Grenzanbieter an, schneidet in der
Gesamtgrößenbetrachtung die Erlösfunktion, die Kostenfunktion gerade an der
Kapazitätsgrenze. Das heißt der Anbieter kann mit seinen Erlösen gerade die Kosten decken
und erzielt keinen Gewinn.
In der Grenzgrößenbetrachtung schneiden die Totalendurchschnittskosten(TDK) bei der
Kapazitätsgrenze den Angebotspreis. Das heißt dass der Anbieter bei voller Auslastung
gerade seine fixen und variablen Kosten decken kann, aber keinen Gewinn erzielt.
2. Angebotsfunktion
Unterstellen sie eine lineare Angebotsfunktion auf dem Markt für Waschmaschinen. Was
passiert wenn der Staat
a) eine Stücksteuer pro verkaufter Waschmaschine erhebt oder
b) eine Subventionssumme pro verkaufter Waschmaschine gewährt?
c) Was passiert mit der Angebotsfunktion, wenn sich die Nachfrage nach Waschmaschinen
erhöht?
a) + b)
P
P
t
Z
Waschmaschinen
t Steuer pro Waschmaschine
c) keinen Einfluss!!
Waschmaschinen
Z = Subvention pro Waschmaschine
4. Stunde Markt, Marktformen und Marktgleichgewicht
Die Marktnachfrage und das Marktangebot werden durch die speziellen
Nachfrage- und Angebotsfunktionen
(N)
X = 140 - 10 * P
(A)
X = - 10 + 5 * P
a) Stellen Sie die Nachfrage- und Angebotskurve in einem Preis-MengenDiagramm dar. Ermitteln Sie grafisch die Gleichgewichtsmenge und den
Gleichgewichtspreis.
Nachfragefunktion
P
0
1
2
3
4
5
6
7
8
9
10
11
12
13
14
X
140
130
120
110
100
90
80
70
60
50
40
30
20
10
0
Angebotsfunktionktion
X
0
0
0
5
10
15
20
25
30
35
40
45
50
55
60
b) Bestimmen Sie algebraisch die Gleichgewichtsmenge und den
Gleichgewichtspreis.
Wie verändert sich die Gleichgewichtsmenge und der Gleichgewichtspreis für
ein normales Gut X, wenn
Die Nachfrage nach X sinkt?
Das Angebot an X steigt?
Die Nachfrage nach X steigt?
Das Angebot an X sinkt?
Gleichgewichtsmenge und Preis sinken
Gleichgewichtsmenge steigt, Preis sinkt
Gleichgewichtsmenge und Preis steigen
Gleichgewichtsmenge fällt und Preis steigt
c) Welche charakteristischen Merkmale weist ein vollkommener Markt auf?
Siehe Folie 89/90
Idealvorstellung:
Homogene Güter: angebotene und nachgefragte Güter sind sachlich gleichartig!
Güter werden von Nachfragern als gleichartig angesehen.
d) Wann spricht man von der Marktsituation der vollständigen
Konkurrenz
Polypol + ein vollkommener Markt als wichtige Voraussetzungen für die
Situation der vollständigen Konkurrenz! Siehe Folie 93
2. Monopolfall
Ein Allgäuer Stadtverkehranbieter ist ein Monopolist in der Stadt Kempten für
den Personennahverkehr. Er sieht sich als Monopolist einer Preisabsatzfunktion
gegenüber mit folgender funktionalen Beziehung für das Preis-Absatzverhalten:
P = - X + 8
Interpretieren Sie diese Funktion des Monopolisten! Stellen Sie diese PAF in
einem Preis-Mengen-Diagramm dar! Siehe Folie 157
i)
Seine Kostenfunktion lässt durch folgende lineare Beziehung
darstellen:
K = 3 * X + 4
Entwickeln Sie ein Tabelle, wo sie für die Preise 3; 4; 5; 6; 7 und 8
die Menge,
den Erlös,
den Grenzerlös (Begründen Sie den Verlauf dieser Funktion!), Nachfrage steigt
nicht in gleicher Relation wie der Preis abnimmt. Nachfrage ist irgendwann
erschöpft
die Gesamtkosten,
die Grenzkosten
die totalen Durchschnittskosten,
den Gewinn,
und den Stückgewinn ermitteln.
Zeichnen Sie sowohl in Gesamtgrößenbetrachtung als auch in
Grenzgrößenbetrachtung die gewinnmaximale Situation des Monopolisten.
d) Berechnen Sie die Cournot´sche Lösung für diesen Beispielfall:
Man Ermittelt den Gewinnoptimalen Monopolpreis für den Anbieter, indem
man vom Schnittpunkt der Grenzerlös- und Grenzkostenkurve senkrecht nach
oben auf die Nachfragekurve geht und von dort horizontal zur Preisachse
wechselt. Die so gefundene Preis-Mengen-Kombination C heißt Cournotscher
Punkt.
- der Grenzgewinn = 0
- der Abstand zwischen Erlös- und Kostenkurve maximal
- damit auch der Gewinn maximal