Institut für Mathematik Seminar: Differentialgleichungen in der
Werbung

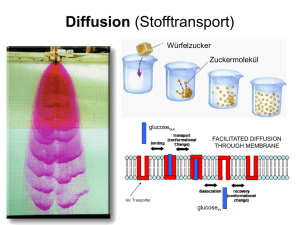
Institut für Mathematik Seminar: Differentialgleichungen in der Biomedizin Dozent: Prof. Dr. Martin Burger Referentin: Natalie Emken SoSe 2009 27.05.2009 Zellmembrane 1. Die Zellmembran 1.1 Aufbau 1.2 Aufgaben der Membranproteine 1.3 Transportmechanismen 2. Diffusion 2.1 Ficksches Gesetz 2.2 Diffusionskoeffizienten 2.3 Diffusion durch eine Membran 3. Erleichterte Diffusion 3.1 Erleichterte Diffusion von Sauerstoff 3.2 Erleichterte Diffusion bei der Muskelatmung 4. Carrier-vermittelter Transport 4.1 Glucosetransport 4.2 Symport und Antiport 5. Aktiver Transport 5.1 Die Natrium-Kalium-ATPase 5.2 Die Calcium-ATPase 6. Das Membranpotential 6.1 Das Nernst-Gleichgewichtspotential 6.2 Die Goldman-Hodgkin-Katz-Gleichung 7. Osmose 8. Kontrolle des Zellvolumen 1 Formelsammlung Das Ficksche Gesetz: Der Fluss J eines chemischen Stoffes u ist gegeben durch J Du D bezeichnet den Diffusionskoeffizient des Ions. D.h. die Teilchenstromdichte J ist proportional zum Konzentrationsgradienten entgegen der Diffusionsrichtung. Die Diffusionsgleichung: Die Diffusion eines chem. Stoffes u mit lok. Produktionsrate f ist gegeben durch u D² u f t Sie stellt damit eine Beziehung zw. zeitlichen und örtlichen Konzentrationsunterschieden dar. Das Membranpotential: Das Membranpotential einer Membran ist gegeben durch V=Vi-Ve Vi und Ve bezeichnen jeweils das intrazellulare und das extrazellulare elektrische Potential. Das Nernst-Potential: Das Gleichgewichtspotential eines Ions ist gegeben durch Vs RT S e kT S e ln ln zF S i zq S i Hierbei bezeichnet R die allgemeine Gaskonstante, T ist die absolute Temperatur, F ist die FaradayKonstante, k ist die Boltzmann-Konstante, q ist die Landung von dem Ion S und S i und S e bezeichnen die intrazellulare und extrazellulare Konzentration von S. Plancks Gleichung: Der Beitrag zu dem Fluss eines Ions durch das Kraftfeld ist gegeben durch J u z c z Hierbei ist u die Beweglichkeit des Ions, z dessen Ladungszahl, c bezeichnet die Konzentration von S und Ф ist das elektrische Potential. Die Nernst-Planck-Gleichung: Der Fluss eines Ions, angetrieben durch den elektrochemischen Gradienten, ist gegeben durch zF J D c c RT Die Goldman-Hodgkin-Katz (GHK)-Gleichung: Die elektrische Stomdichte eines Ions S ist gegeben durch zFV ci ce exp z² F ² RT IS PS V RT zFV 1 exp RT D ist die Permeabilität der Membran für das Ion S L Der Membranstrom IS, der durch das Ion S zu einem best. Zeitpunkt getragen wird kann auch folgendermaßen ausgedrückt werden IS=g(V-VS) (g=1/r ist die Membranleitfähigkeit) PS Der osmotische Druck: πs=kcT Hierbei bezeichnet c die Konzentration des gelösten Stoffes in Molekülen pro VE. 2