VEROFFPP1_korr_2014_9_25

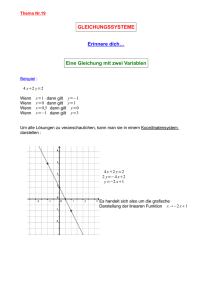
1
(VEROFFPP1_korr_2014_9_25.doc)
korrigierte Version vom 25.9.2014
Erstveröffentlicht in:
Vereinigte Fachverlage, antriebstechnik 38 (1999), Seite 43 ff.
1.
2.
3.
4.
5.
6.
7.
Einführung
Die Struktur der Regelung
Die Clarke-Park-Transformation und deren Inverse
Betrachtungen zu den zwei PI-Reglern
Erzeugung der Resolverwertes
Bemerkungen zur Hard- und Software
Zusammenfassung und Ausblick
Zusammenfassung.
Blödow, Friedrich, Prof. Dr.-Ing.
Digitale Stromregelung eines Linear-Synchron-Motors.
Es wird die Stromregelung eines Linear-Synchron-Motors mit Hilfe eines digitalen
Signalprozessors (DSP TMS320F240) beschrieben. Die Grundstruktur der Regelung
beinhaltet die Clarke-Park-Transformation. Besonders intensiv wird auf die
Auslegungskriterien der vier Parameter der beiden PI-Regler eingegangen.
Meinem Doktorvater Univ. Prof. Dr.-Ing. Dr.-Ing. Eh. R. Lunderstädt zum 60. Geburtstag.
Digitale Stromregelung eines Linear-Synchron-Motors.
Abstrakt.
Digitale Signalprozessoren (DSP), die auf einem Silizium-Chip alle für eine Regelung einer
Synchron-Maschine notwendigen Funktionen integriert haben, sind erst seit ca. Anfang
1998 den Hochschulen verfügbar. Mit der Verarbeitungsgeschwindigkeit dieser SingleChip-DSPs lassen sich momentan Stromregelungen mit einer Abtastrate von 20 KHz
realisieren. Damit können erstmals die Vorteile von digitalen Regelungen , wie z. B.
geringes Driftverhalten und einfache Parametrierung, auch in diesem Bereich konsequent
verwirklicht werden. Am Beispiel eines Linear-Synchron-Motors und dem Single-Chip-DSP
von Texas Instruments TMS320F240 wird die Stromregelung mit Hilfe der Clarke-ParkTransformation besprochen.
1 Einführung.
Für Positionieraufgaben, die eine hohe Präzision (1 µm) und schnelle
Verfahrgeschwindigkeiten (bis 1 m/Sek) verlangen, eignet sich der Linear-SynchronAntrieb besonders, da im Gegensatz zu den rotatorischen Motoren keine Umsetzung der
Drehbewegung in die Längsbewegung benötigt wird. Es entfällt somit z.B. die
1
2
Kugelrollspindel mit ihrer Haftreibung b. z. w. Lose. Durch diesen Direktantrieb entstehen
somit steifere Systeme, die sich noch präziser und schneller regeln lassen.
Auch die Luftlagerung ist damit praktisch realisierbar geworden, was ebenfalls der
Präzision zu Gute kommt, mit dem Nebeneffekt, das Haftreibungen nun real
vernachlässigbar
sind.
Eingesetzt
wird
diese
Technik
u.a.
in
Leiterplattenbearbeitungsautomaten der Firma WESSEL. Im Synchron-Linear-Motor muß
nun, um eine Positionierregelung aufbauen zu können, im ersten Schritt, wie auch in den
rotatorischen Motoren, der Strom geregelt werden. Dies kann analog oder digital erfolgen,
wobei die digitale Regelung u.a. hinsichtlich der Bauteile- und Produktionskosten Vorteile
bietet. In diesem Beitrag wird die digitale Stromregelung mit einem digitalen
Signalprozessor über die Vektor-Kontroll-Methode besprochen, die analog nur unter
erheblichen Mehrkosten zu realisieren ist. Dieses Regelungskonzept ergibt eine
hervorragende Dynamik-Performance, und konstante vorgebbare Beschleunigungswerte
bei allen Geschwindigkeiten, wobei der Vier-Quadranten-Betrieb mit inbegriffen ist. Die
Vektor-Kontroll-Methode über die
Clarke-Park-Transformation entkoppelt den
Polradwinkel von der Beschleunigung, womit als einzige Eingangsgrößen in das System
die Beschleunigung vorgegeben werden kann. Auf die vier Parameter der beiden PIRegler, die in diesem Konzept einzustellen sind, wie auf die Berechnung des notwendigen
Resolverwertes aus dem Positionswert, der naturgemäß bei einem Linear-SynchronAntrieb zunächst nicht vorhanden ist, wird besonders eingegangen.
2. Struktur der Regelung.
Bild 1 zeigt die Struktur der Regelung. Die zu regelnde Strecke, ein Linear-SynchronMotor, der in einem Maschinenbett einer Leiterplattenbohrmaschine der Firma Wessel
integriert ist, wird im unteren Teil von Bild 1 gezeigt. Als Meßglieder sind ein
HEIDENHAIN-Längenmeßsytem mit 40 µm Teilungsperiode, und zwei LEM-Hall-StromSensoren eingesetzt worden. Aus dem Längenmeßsystem wird der Resolverwert
berechnet, und die beiden Stromsensoren erfassen die Ströme in zwei Phasen des
Motors. Zur Messtrecke werden auch der Analog-Digital-Wandler und die Clarke-ParkTransformation gezählt. Die Ausgangsgrößen der Clarke-Park-Transformation
entsprechen dem Polradwinkel und der Beschleunigung. Da der Polradwinkel f bei einem
Linear-Synchron-Motor zu Null geregelt wird, fehlt verständlicherweise der
Summationspunkt vor dem PI-Regler 2. Lediglich das eingezeichnete P-Glied mit der
Verstärkung -1 repräsentiert rudimentär den Summationspunkt. Der zweite
Summationspunkt vor dem PI-Regler 1 bildet die Differenz zwischen der SollBeschleunigung und der Ist-Beschleunigung, die der Regler dann verarbeitet. Die
Ausgänge der beiden PI-Regler werden in die inverse Clarke-Park-Transformation
geleitet, die ihrerseits als Ausgangsgrößen die notwendigen Spannungen der drei Phasen
liefert. Der hierauf folgende Pulsweiten-Modulator (PWM 20KHz) und das Leistungsteil,
bestehend aus 6 Leistungshalbleitern zusammengeschaltet zu drei Halbbrücken, sind als
das Stellglied des Regelkreises zu betrachten. Damit ist der Regelkreis geschlossen.
2
3
Texas Instruments
DSP TMS320F240
Inverse
ClarkePark
PI 2
ibPI
PWM
icPI
20 KHz
2 LEM-Strom-Wandler
Beschleunigungssollwert
PI 1
iaPI
ia
isd
Clarke-
isq
Ib
Park
A/D
10 Bit

Resolverwert
HAIDENHAIN Stahllineal 40µm Teilungsperiode
BAUTZ Synchron-Linear-Motor
WESSEL Maschinenbett
Bild1: Struktur der digitalen Stromregelung.
3. Die Clarke-Park-Transformation und deren Inverse
Die Clarke-Park-Transformation bildet die drei Strangströme einer Linear-SynchronMaschine in Abhängigkeit der Stellung der Magnetfelder zueinander (Resolverwert) in ein
rechtwinkliges Koordinatensystem ab, wobei auf der Abszisse die Beschleunigung
aufgetragen wird und auf der Ordinate der Polradwinkel. Regelungstechnisch gesehen
besitzt die Transformation also drei Eingangsgrößen, die Ströme ia und ib und den
Resolverwert ( der dritte Strom ergibt sich aus ic = -ia -ib), und zwei Ausgangsgrößen, die
Beschleunigung und den Polradwinkel. Die Gleichungen lauten
2 
 1
i sq   sin(  )  i a  cos( )  
ia 
ib 
3 
 3
(1)
3
4
, und
 1
2 
isd  cos( )  ia  sin(  )  
ia 
ib 
3 
 3
(2)
mit isq der Beschleunigungskomponenten , isd der Polradwinkelkomponenten, 
dem Resolverwert, und ia und ib den beiden Strangströmen.
Ein Polradwinkel verschieden Null verschlechtert den Wirkungsgrad einer
Synchronmaschine, deshalb wird dieser zu Null geregelt. Damit verbleibt als Sollwert für
die Regelung die Beschleunigung. Die beiden Ausgangsgrößen dieser beiden Regler
werden zusammen mit der Resolverinformation in die inverse Clarke-Park-Transformation
geleitet, die daraufhin die drei Strangstrominformationen liefert. Die Gleichungen der
inversen Clarke-Park-Transformation lauten
iaPI  isdPI  cos( )  isqPI  sin(  )
(3),
1
3
i bPI    i sdPI  cos( )  i sqPI  sin(  )  
 i sdPI  sin(  )  i sqPI  cos( ) 
2
2
(4),
und
1
3
i sdPI  sin(  )  i sqPI  cos( )
i cPI    i sdPI  cos( )  i sqPI  sin(  )  
2
2
(5),
mit iaPI, ibPI und icPI den Strominformationen, die über die PWM den Leistungstransistoren
zugeführt werden,  der Resolverinformation, und isdPI und isqPI den Ausgangsgrößen der
beiden PI-Regler.
4. Betrachtungen zu den zwei PI-Reglern
Der PI-Regler wird im Zeitbereich über die Gleichung (6)
T
y PI  k I  e(t )dt  y PI 0  k P  e(t )
(6)
0
beschrieben, mit kI und kP den einzustellenden Regelparametern, e(t) der Eingangsgröße
in den PI-Regler und yPI0 der Anfangsbedingung. Durch einmaliges Differenzieren der
Gleichung (6) und Transformation in den Bildbereich erhält man die Gleichung (7)
4
5
1
YPI ( s)  k I
kP
s
kI
E (s)
s
(7)
Deutlich ist im Zähler der Gleichung (7) ein Hochpaß mit der Zeitkonstanten
TH 
kP
kI
(8)
zu erkennen. Dieser Hochpaß wird i. a. auf den Tiefpaß der Strecke gelegt. Im Falle des
Linearmotors lautet die Gleichung des Tiefpasses
1
I (s)  R U (s)
L
1 s
R
(9)
mit U(s) der Eingangsspannung an einer Phase und I(s) dem Strom in der Phase. Bildet
man jetzt die Übertragungsfunktion des offenen Kreises, mit
kP L

kI R
(10)
,setzt also die Zeitkonstante des Hochpasses gleich der Zeitkonstanten des Tiefpasses, so
verbleibt der Ausdruck (11)
kI
I ( s)
G0 
 R
E ( s)
s
(11)
Nun kann der Regelkreis geschlossen werden, und die Führungsübertragungsfunktion
(12) lautet zunächst allgemein
Gw 
G0 ( s )
1  G0 ( s )  G M ( s )
(12)
mit GM(s)=1 und der Einheit V/A.
Wird jetzt (11) in (12) eingesetzt und umgeformt, erhält man die Gleichung (13)
5
6
G w ( s) 
1
R
1
s
kI
(13)
oder etwas anschaulicher die Gleichung (14)
I ( s) 
1
W ( s)
R
1
s
kI
(14)
mit I(s) dem Strom in der Phase und W(s) dem Stromsollwert als Spannung. Es ist also
durch die Regelung hinsichtlich des Stromes ein Tiefpaß mit der Zeitkonstanten
Tneu  R
kI
(15)
entstanden, wobei diese Zeitkonstante über kI i. a. so gewählt wird, daß die Zeitkonstante
Tneu 1/10 der alten Zeitkonstante L/R beträgt. Damit schwingt der Strom um den Faktor 10
schneller ein, als ohne Stromregelung. Eine Regelabweichung ist laut Gleichung (14) nicht
vorhanden. Diese Vorgehensweise ist in analogen Regelungen im vollem Umfange
realisierbar. (Hinweis: Die Einheitenkontrolle ist unter Berücksichtigung des Meßgliedes
mit der Einheit V/A im Nenner der Gleichung (15) durchzuführen)
Im Falle einer digitalen Regelung sind zwei weitere Aspekte zu betrachten:
Es ist zum einen die Abtastzeit. Sie muß so klein sein, daß die Regelung als
quasikontinuierlich betrachtet werden kann. Das ist dann der Fall, wenn die schnellste im
System zu bearbeitende Zeitkonstante mindestens 10 mal abgetastet wird. Dies trifft in
dem hier beschriebene Fall zu. Der zweite Aspekt betrifft die Auflösung des AnalogDigital-Wandlers, hier 10 Bit. Da der Strom positive, wie negative Werte annimmt, wird ein
Bit für das Vorzeichen benötigt. Es verbleiben somit 9 Bit entsprechend 512 Stufen. Wie
bekannt, entspricht jede klassische digitale Regelung bei Erreichen des stationären
Endwertes einer Zweipunktregelung. Diese Zweipunktregelung schwingt in diesem Fall um
das last significant bit des Analog-Digital-Wandlers, wenn nicht Verstärkungsfaktoren im
Regelkreis dieses Quantisierungsrauschen verstärken. Da das Quantisierungsrauschen
des Stromes direkt über den Soll-Ist-Wertvergleich vor dem PI-Regler mit dem kP des
Reglers multipliziert wird,
werden KP-Werte größer 1 das Quantisierungsrauschen
proportional verstärken. Die Vorgehensweise zur Bestimmung von kP ist nun die folgende:
Zunächst wird kP=1 gewählt, hieraus das kI berechnet und die Stromregelung erstmalig in
Betrieb genommen.
Danach wird kP Stückweise erhöht, mit gleichzeitiger Berechnung von kI , bis
Schwingungen in der Regelung auftreten und/oder das Rauschen akustisch bewertet ein
nicht vertretbares Maß angenommen hat.
6
7
Dieser kP -Wert ist zu 100% anzusetzen und dann auf 75% zu reduzieren, um eine
entsprechende Sicherheitsabstand für Parameterschwankungen bereitzustellen.
Bei
vorgegebenem kP berechnet sich das kI aus der Gleichung (10) zu
kI  kP 
R
L
(16),
mit L/R der elektrischen Zeitkonstanten des Antriebes. Diese kann aus den Daten der
Maschine entnommen werden, oder wie hier, meßtechnisch
ermittelt werden.
Aufgrund der beschriebenen Vorgehensweise wurde ein kP von 2 gewählt.
Bild 2 zeigt die Stromsprungantwort in den Phasen ia und ib gemessen an den Ausgängen
der LEM-Stromwandler in geregeltem Zustand. Die Zeitkonstante beträgt ca. 1,5
Millisekunden, d. h. in 1,5 Millisekunden sind 63% des Stromsollwertes bereits erreicht.
Bild 2: Stromsprungantwort in den Phasen ia und ib.
7
8
5. Erzeugung des Resolverwertes
Um in dem Motor eine kontinuierliche Beschleunigung verwirklichen zu können, muß stets
die Lage der Magnetfelder zwischen Primär und Sekundärteil bekannt sein, ansonsten
wäre es nicht möglich, die Magnetfelder über die Ströme entsprechend zu regeln. Da bei
Linear-Motoren ein derartiger Sensor nicht kostengünstig realisierbar ist, wird der
Resolverwert aus der Position des Primärteiles berechnet. Wie dies mit den Single-ChipDSP realisiert wurde, zeigt das nachstehende Programmstück. Selbstverständlich ist die
Kommutatorlänge und die Auflösung des Längenmeßsystems bekannt.
; Wandle Inkrementalwert des Längenmeßsystems
; posilow und posihigh = 32-Bit-Signed zum Resolverwert
; Eingang : posilow und posihigh, die Kommutatorlaenge und Komuscale.
; Ausgang: Resolverwert im Bereich 0 bis ffffh entsprechen 0 bis 360 Grad = Winkel
; Dies Routine benötigt ein Grundzeit von 2. µ-Sek.,
; jeder weiterer Add- oder Sub-Durchlauf benötigt weitere 250 n-Sek.
; ***********************************************************************
resol
ldp
#dp300
setc
sxm
;
bit
posihigh,bit15 ; teste Vorzeichen
bcnd relo1,tc
; Bit32=1 negativ
;------------------ position ist positiv
clrc
sxm
lacc
posihigh,16
; Bit32=0 von posihigh
add
posilow
; lade den accu 32 bit
setc
sxm
; damit sub ueber 32 bits
relo3 sub
kommulaenge ; Wert positiv, subtrahiere so lange, bis negativ
bcnd relo3,geq
; immer noch positiv
add
kommulaenge ; jetzt negativ, schiebe durch Addition in den in positiven Bereich
sacl
resolver
; Zwischenergebnis, normiere jetzt auf 0 bis ffffh
clrc
sxm
;
lt
resolver
;
mpy
komuscale
;
pac
; preg in den accu
sacl
resolver
; Ergebnis sichern
sub
#0ffffh
bcnd relo6,leq
; alles o. k.
lac
#0ffffh
; Multiplikation ergab größer ffffh = Rundungsfehler
sacl
resolver
; korrigiere diesen Fehler
b
relo6
; fertig
;------------------------- Position ist negativ
relo1
clrc
sxm
lacc
posihigh,16
; Bit15 1 von posihigh
add
posilow
; lade den accu 32 bit
setc
sxm
; damit add ueber 32 bits
relo4 add
kommulaenge ; Wert neg, add so lange bis positiv
bcnd relo4,leq
; immer noch negativ
sub
kommulaenge ; pos, schiebe durch sub zurueck in den neg. Bereich
abs
; mache pos
sacl
resolver
; Zwischenergebnis, normiere jetzt auf 0 bis ffffh
clrc
sxm
;
lt
resolver
;
mpy
komuscale
;
pac
; preg in den accu
8
9
neg
sacl
sub
bcnd
lac
sacl
b
resolver
#0ffffh
relo6,leq
#0ffffh
resolver
relo6
;
; sichere Ergebniss
; alles ok
; multi ergab größer ffffh=Rundungsfehler
; korrigiere diesen Fehler
relo6:
lac
sacl
ret
resolver
winkel
; = Kommutatorwinkel 0-360 Grad => 0-ffffH
6. Bemerkungen zur Hard- und Software
Der Kern der Hardware ist ein Festkomma 16 Bit digitaler Chingle-Chip-Signalprozessor
TMS320F240 von Texas Instrument. Er wird mit 50 n-Sekunden getacktet und führt ca.
90% seiner Befehle innerhalb dieser Zeit auch aus. Auf dem Chip integriert in ein
Zweikanal 10 Bit-Analog-Digital-Wandler mit jeweils 8 Kanälen zur gleichzeitigen
Wandlung der beiden Strangströme. Zur Erfassung und Aufbereitung von inkrementalen
Signale aus dem Längenmeßsystem ist ebenfalls eine 16 Bit-Einheit vorhanden. Die
Ausgabeeinheit, der Pulsbreitenmodulator, kann im asymmetrischen, im symmetrischen
und im Space-Vektor-Mode betrieben werden. Im symmetrischen Mode und SpaceVektor-Mode werden PWM-Frequenzen von 10 KHz erreicht, was im Zusammenhang mit
den dynamischen Anforderungen der Anwendung als nicht ausreichend bewertet wurde.
Auch die Vorteile der Space-Vektor-PWM scheinen durch die Veröffentlichung [1]
relativiert worden zu sein. Mit der verwendeten asymmetrischen PWM wurde eine
Frequenz von 20 KHz erreicht.
Die Software wurde ausschließlich in Assembler mit Unterstützung eines C-Compilers
geschrieben. Bereichsabfragen mit 32-Bit-Variablen, wie z. B.
If((input<=constante1)||(input>=constante2 ))
wurden in C formuliert, danach in die ASM-Memonik übersetzt, aufbereitet und erst dann
implementiert. Die Clarke-Park-Transformationen, die Sinus- und Cosinus-Berechnungen
und weitere Routinen wurden aus den Veröffentlichungen [2, [3], [4], [5], und [6]
entnommen, während die PI-Regler selbst entworfen wurden. Auch wurde die Anzahl der
Stützstellen zur Berechnung der Sinus- und Cosinuswerte zwecks Steigerung der
Genauigkeit von128 auf 256 Stützstellen erhöht. Besondere Aufmerksamkeit ist dem
Wind-Up-Effekt in den PI-Reglern zu schenken. Die Durchlaufzeit durch die gesamte
Software beträgt 45 µ-Sekunden.
7. Zusammenfassung und Ausblick
Der Stromregelkreis in einer Positionierregelung ist der schnellste Regelkreis in dem
System. Um einen Vorstellung von der Geschwindigkeit zu vermitteln, sei die
Positionierzeit einer Leiterplattenbohrmaschine von Loch zu Loch mit 200 Millisekunden
vorgegeben. Damit teilt sich der Positioniervorgang auf in 100 Millisekunden für das
Beschleunigen und 100 Millisekunden für das Bremsen auf. Wird der Positionierregelkreis
mit einer Taktrate von 2 Millisekunden betrieben, so fallen 50 Abtastungen auf den
9
10
Bremsvorgang, was eine gutes, aber kein hervorragendes Positionierverhalten ergibt. In
der dreifachen Positionierkaskade ist der Positionierregelkreis der äußerste, der Mittlere ist
der Geschwindigkeitsregelkreis, und der Innerste ist der Stromregelkreis. Um
hervorragende Ergebnisse zu erzielen, sollte davon ausgegangen werden, daß der
Mittlere Regelkreis (Geschwindigkeitsregelkreis) um den Faktor 5 schneller einschwingt,
als der Positionsregelkreis, und der innerste Regelkreis (Stromregelkreis) wiederum ein
um den Faktor 5 schnelleres Einschwingverhalten zeigen sollte. Damit ergibt sich für den
Stromregelkreis eine Zeitkonstante von 80 µ-Sekunden. Wird dieser Regelkreis digital
ausgeführt, so sollte auf diese Zeitkonstante 10 Abtastungen fallen. Dies ergibt eine
Rechenzeit von 8 µ-Sekunden in der die gesamte Stromregelung abgearbeitet sein muß.
Eine Forderung, die mit den momentan für diesen Zweck verfügbaren Digitalrechnern
nicht zu realisieren ist. Das in diesem Beitrag gezeigte Beispiel erreicht eine Rechenzeit
von 50 µ-Sekunden, was eine Zeitkonstante von 500 µ-Sekunden für den Stromregelkreis
ergeben kann und damit an der Spitze des marktüblichen liegt. Aus dieser Sicht ist eine
optimale digitale Regelung noch nicht erreicht, aber immerhin liegt lediglich ein Faktor von
6,25 von dem
optimalen Verhalten entfernt. Eine andere Möglichkeit wäre, die
Stromregelung über den Zustandsraum mit linearem Regelgesetz zu verwirklichen. Erste
Untersuchungen sind erfolgversprechend.
Die Nachteile des PI-Reglers im
Zusammenhang mit der eingesetzten Pol-Nullstellen-Kompensation,
die in der
Grundstruktur die bekannten Parameterempfindlichkeiten beinhaltet, treten im
Zustandsraum nicht auf. Auch zeigen erste Untersuchungen kleinere Rechenzeiten, da
nur die inverse Clarke-Park-Transformation abgearbeitet werden muß. Es ist vorgesehen,
nach Beendigung dieser Untersuchungen, die Ergebnisse zu veröffentlichen.
Literatur:
[1] Zhenyu, Yu; Figoli, David;
AC Induction Motor Control Using Constant V/Hz Principle and Space Vector PWM
Technique with TMS320C240.
Application Report: SPRA284A,
Texas Instruments, April 1998.
[2] Alter, David M.;
Obtaining Absolute Encoder Position on a TMS320C240
Application Brief: SPRA279,
Texas Instruments, July 1997.
[3] N.N ;
Field Orientated Control of 3-Phase AC-Motors.
Application Report: BPRA073,
Texas Instruments, February 1998.
[4] N.N ;
Table Look-up and Interpolation on the TMS320C2XX
Application Report: BPRA046
Texas Instruments, 1997.
[5] N.N ;
Sine, Cosine on the TMS320C2XX
10
11
Application Report: BPRA047
Texas Instruments, 1997.
[6] N.N ;
Clarke & Park Transformation on the TMS320C2XX
Application Report: BPRA048
Texas Instruments, 1997.
11